海铁并行联运战略投送优化模型与算法

高忠印,王 诺

(大连海事大学交通运输工程学院,辽宁大连 116026)

1 引 言

所谓战略投送,通常是指将军事力量快速投送到战略前线的一种军事行动[1].近年来,随着两岸统一呼声的日益高涨,某大国军舰多次进入台湾海峡炫耀武力,一小撮台独分子也蠢蠢欲动,极力阻挠两岸统一.在这一形势下,开展战略投送方案优化研究,在军事上进行必要的准备,对于警告外国势力,震慑台独,推动两岸早日统一意义重大.

目前对战略投送的研究已有一些成果,如战略投送过程的常用模式[2,3],我国战略投送面临的问题及体系建设[4].在战略投送的运输方面,文献[5–7]提出了增强海上和铁路远程运输能力的有效方法,但这些研究仅仅是对战略投送能力进行分析并给出相关建议,并没有从定量的角度进行分析研究.关于战略投送方案的优化模型,文献[8,9]构建了应急中心选址及车辆安排的双目标混合整数规划模型;文献[10]提出了情景推演贝叶斯网络模型;文献[11]针对灾害情景中的应急运输问题,建立了整数线性规划模型.

海铁并行联运问题属于多种运输方式中下水港选择及路径寻优, 属于特殊的选址–路径优化问题(location-routing problem,LRP).关于LRP 问题的优化,文献[12,13]针对选址–路径优化问题的整数规划模型采用两阶段启发式算法进行求解;文献[14]运用鲁棒优化方法,将选址–路径优化模型转化为易求解的鲁棒等价模型;文献[15]将遗传算法和局部迭代搜索算法相结合后对选址–路径问题进行优化;文献[16,17]提出一种自适应多种群的混合算法进行求解;文献[18–20]考虑了选址–路径优化方面的多重约束,先用聚类分析模型解决选址问题,然后设计算法求解;文献[21]分析了配送中心的配送模式,建立了组合模型,并利用混合算法进行求解;文献[22,23]介绍了LRP 问题扩展类型及其他优化方法;文献[24]基于运输方式的多样性,建立了选址–多式联运路径优化模型,采用Dijkstra 改进算法和O-D 矩阵搜索算法进行求解;文献[25]以总成本最低为目标,建立了混合整数规划模型对多种运输方式之间的选择进行优化;文献[26]建立了带有时间约束的0-1 整数规划模型来解决战略投送网络选址问题.

上述文献为我国的战略投送能力建设和方案优化提供解决思路,分析已有成果发现,尽管有关路径优化的研究较多,但针对海铁协同并进及联运的路径优化问题却鲜有提及,尤其是在多种运输方式协同运输的优化算法上还缺少深入研究.与以往单一或多式联运的运输方式相比,本文需要解决的难点在于问题不仅包含有海铁联运,还包括海铁协同并行运输,变量较多,内容交叉,需综合考虑各集结地、下水港(即始发港,下同)、上水港(即登陆港或终点港,下同)和终点站之间的相对距离来统筹优化.在投送过程中,海运下水港及海陆运输路线难以选择,船舶在港口的等待时间难以确定等,使其优化过程将更为复杂多变.需要优化的内容包括: 运输方式和下水港的选择,船舶航次数量、每个航次中的挂靠港以及每个挂靠港装载人员和装备数量的决策;铁路专列班次数量、每个班次的中转站以及每个中转站装载人员和数量的决策等等.针对上述问题,本文面向海铁并行联运开展战略投送方案优化研究,其主要创新点有两个:1)构建了既有海铁并行又有联运的路径优化模型;2)对求解算法进行组合重构,将改进的禁忌搜索算法(TS)嵌入到遗传算法(GA)之中,形成内外协同优化的集成算法(GTSA).为验证所设模型和算法的有效性,以我国各战区向东海前线投送为例进行分析,得到了较优方案.通过与其他算法进行对比以及敏感性分析,证明了本文算法在解决此类问题上的有效性.

2 海铁并行联运战略投送优化模型

2.1 基本问题

为进行战略上的军事装备,需要向指定地点紧急运送军事力量.由于战略投送的人员和重型装备(以下简称为装备)在数量上均较大,而铁路运输所需的专用车辆数量有限,若全部采用铁路运输会受到专用列车数量的限制,导致等待时间增长,所需的运输时间增加;同样,全部采取海运也会受到滚装船数量的限制.因此,考虑到我国北方地区海上运输较为便利,故采取海铁协同并进的运输方式,即有的集结地选择海铁联运方式,有的选择完全由铁路运输,两种方式的运量相互协调,以达到整体战略投送时间最短的最佳效果.在具体操作上,若选择海铁联运方式,则需要利用铁路运输将该集结地的人员和装备运输至指定下水港,同时在下水港附近调用商用客货滚装船(以下简称船舶).投送时,船舶需要赶到指定的下水港,进行装载后到达指定地区的登陆港.若选择完全以铁路运输方式,则需征调适宜装备和人员运输的专用车辆.投送时,专用车辆需要赶到运输集结地,装载后组成专列到达指定地区的铁路终点站.如此循环往返,直至所有装备和人员投送至指定地区.

由上述过程可知,本文构建的海铁协同并进的战略投送是由不同运输方式选择、海上运输优化和铁路运输优化3 部分内容构成.在优化过程中,海上运输与铁路运输是相互影响的两个方面: 如全部选择海上运输,则船舶需多次往返,铁路运输能力未充分利用,运输时间增加;如全部选择铁路运输,则专列需多次往返,海上运力没有充分利用,运输时间也将增加,如何在这两种运输方式之间优化平衡是需考虑的第1 个问题.对于海上通道的选择,若各战区出发时都以距离最近的港口出海,则会导致船舶靠离泊频繁,海上运输的时间将随之延长;而若选择少数港口出海,则陆上的运输时间将延长,这是两难的抉择,如何选择并缩减下水港的数量是第2 个问题.另外,对船舶及专列的运输量、航次或班次数量及航线或路线等如何确定是第3 个问题.综上所述,如何解决上述3 个问题是本文所要研究的内容.

2.2 符号设定

为了便于描述,现将模型所需参数和变量的符号设定及含义列于表1 和表2 中.

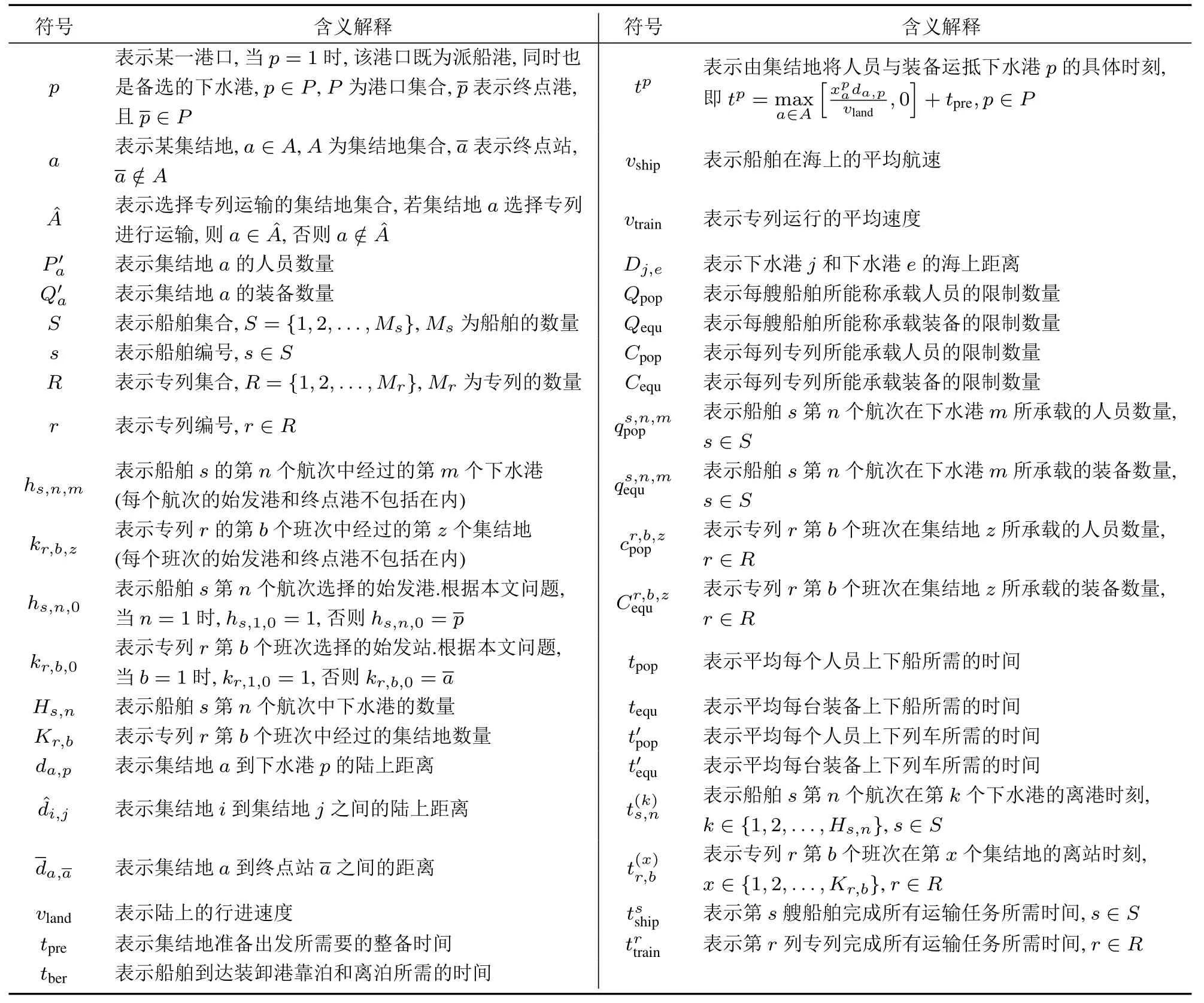
表1 模型参数的符号设定及含义解释Table 1 Symbol setting and meaning interpretation of model parameters

表2 决策变量的符号设定及含义解释Table 2 Symbol setting and meaning interpretation of decision variables

2.3 海上运输时间

由以上分析,设船舶s第n个航次在始发港的离港时刻为

船舶s第n个航次在第1 个下水港的离港时刻为

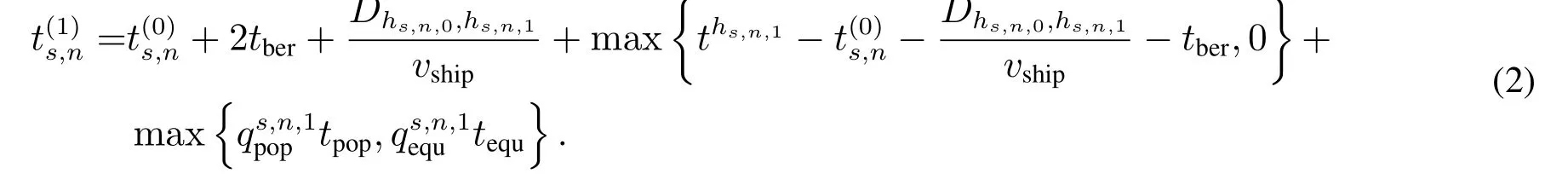
同理,船舶s第n个航次在第2 个下水港的离港时间为

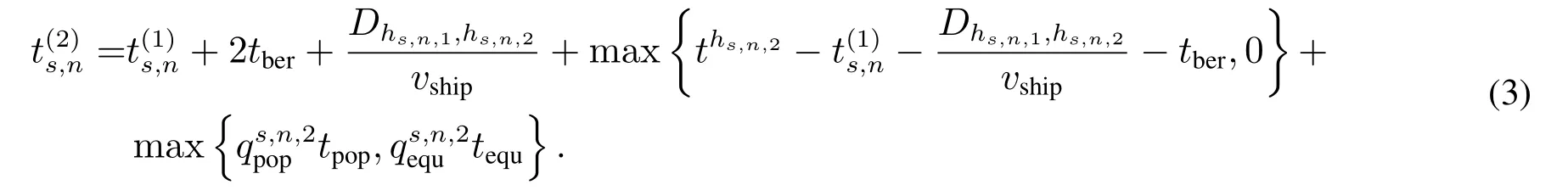
从而,船舶s第n个航次在第k个下水港的离港时刻为

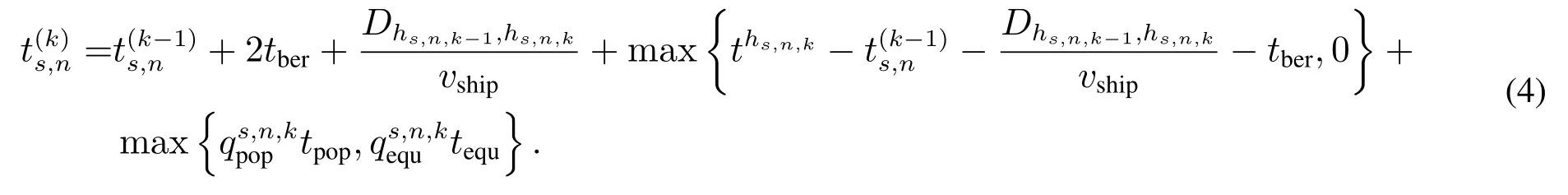
由此可知,船舶s完成所有投送任务的时间为

其中式(5)表示船舶s完成投送任务的总时间由靠离泊时间、海上航行时间、港口等待时间以及港口装卸时间4 个部分组成.

2.4 铁路运输时间

设专列r第b个班次从始发站离开的时刻为

专列r第b个班次从始发站出发经过第1 个集结地的离站时间为

同理,专列r第b个班次在经过第2 个集结地的离站时间为

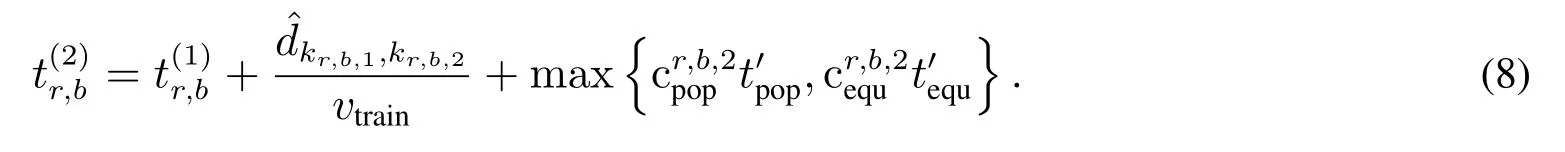
从而,专列r第b个班次在经过第x个集结地的离站时间为

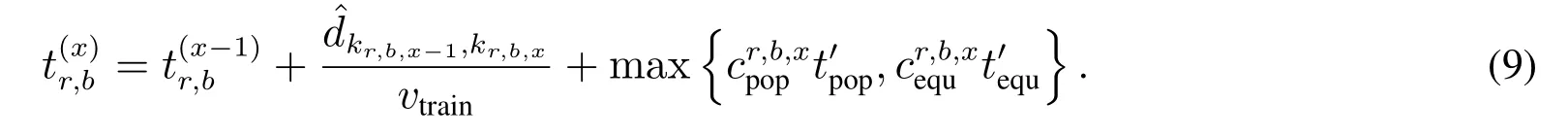
由此可知,专列r完成所有投送任务的时间为

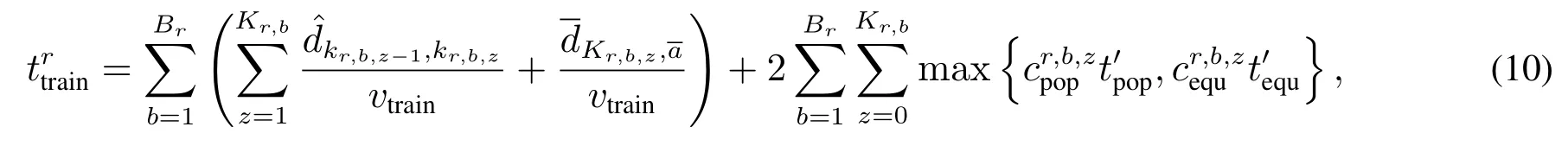
其中式(10)表示专列r完成投送任务的总时间由行驶时间以及装卸时间2 个部分组成.

2.5 海铁联运优化模型

根据以上分析,构建海铁联运优化模型如下

以上模型中,式(11)为目标函数,表示以最短的时间完成海铁协同并进的战略投送任务;约束条件(12)表示每艘船舶各航次途径下水港所装载的人员不超过船舶的最大载人量;约束条件(13)表示每艘船舶各航次途径下水港所装载的装备不超过船舶的最大载货量;约束条件(14)表示每列专列各班次途径集结地所装载的人员不超过专列的最大载人量; 约束条件(15)表示每列专列各班次途径集结地所装载的装备不超过专列的最大载货量; 约束条件(16)表示船舶会服务所有被选为下水港的港口; 约束条件(17)表示每个集结地要么选择海铁联运,要么选择铁路专列进行运输;约束条件(18)表示每一下水港对每艘船舶每个航次仅接受服务1 次; 约束条件(19)表示每1 集结地对每列专列每个班次仅接受服务1 次; 约束条件(20)和约束条件(21)表示所有集结地的人员和装备必须全部投送至目的地.

3 算法设计

本文所建模型变量数目众多、各变量之间的关系纵横交贯,情况复杂,为了快速准确的求解,需针对本文模型的特点构建行之有效的算法.虽然遗传算法全局寻优能力较强,但在针对复杂问题时存在搜索速度慢、稳定性差及早熟的缺点.禁忌搜索算法采用一种独特的记忆功能(禁忌表),通过对最近的搜索过程进行记录来指导下一次搜索的方向,从而避免无效的循环搜索,具有较强的局部搜索能力,但此算法运行机理较为简单,在求解复杂问题时效率会有所下降.综上所述,单一智能优化算法虽各有优势,但在优化海铁协同并进的战略投送这种复杂问题时,由于运算量过大,在参数的选择上要求苛刻,过于依赖初始值,因而在条件不理想时将很难快速获得全局最优的结果.针对此类问题,本文充分利用遗传算法较好的全局搜索能力以及禁忌搜索算法较强的局部搜索能力等优势,并对不足之处进行改进,以期获得运行速度快、计算准确度高、结果稳定性好的求解算法.

本文的算法设计是,将基于仿真的禁忌搜索算法嵌入到遗传算法当中,通过内外之间的协同优化,最终得到最优解.具体做法是: 在外层遗传算法中以染色体表达陆上集结地选择的运输方式以及选择的下水港编号,将外层的染色体信息(包括下水港的编号、集结地的编号)传至内层,内层的禁忌搜索算法根据传入的信息对船舶的航次数量、每个航次的挂靠港、每个挂靠港所装载的人员和装备数量以及专列的班次数量、每个班次的中转站、每个中转站所装载的人员和装备数量进行优化,结合海上运输时间与铁路运输时间计算出目标函数值,再将结果传至外层,利用外层遗传算法进行优化,直至算法收敛为止,具体算法步骤如下:

步骤1开始;

步骤2初始化种群;

步骤3读取种群中的染色体,获取下水港的编号以及集结地编号,并计算各下水港集结人员和装备的数量;

步骤4获取下水港的编号以及集结地的编号生成禁忌搜索算法初始解;

步骤5利用仿真计算初始解的运输时间;

步骤6判断是否满足禁忌搜索终止条件,若满足,则转向步骤9,否则进行下一步骤;

步骤7在初始解的邻域中选取满足禁忌表要求的可行解作为候选集;

步骤8在候选集中选择一个运输时间最短的解,并更新禁忌表,返回步骤5;

步骤9计算个体的适应度值;

步骤10判断遗传算法的终止条件是否满足,若满足则转向步骤,否则进行下一步骤;

步骤11对种群中个体进行选择、交叉、变异,产生新一代种群后转向步骤3;

步骤12输出最优解;

步骤13结束.

3.1 基于运输方式选择的遗传算法设计

1)染色体

设各集结地待运送的人员和装备数量数据见表3.

表3 各集结地待运输的人员和装备数量Table 3 The number of personnel and equipment to be transported in each staging area

首先,以染色体中基因的索引值表示集结地编号,基因表示运输方式以及下水港的选择情况.其次,在生成遗传算法初始解过程中,由于内陆集结地明显不宜采用海运,为了缩小算法的搜索空间,可以基于启发式规则生成初始解.图1 表示1 条可能的染色体,其含义为1#号和2#号集结地的人员和装备选择1#号港口出海,3#号和4#号集结地的人员和装备选择2#号港口出海,5#,6#,7#,8#,9#号集结地选择铁路专列运输至目的地.由该染色体表示的各下水港及各集结地的对应的人员和装备信息如表4 和表5 所示.

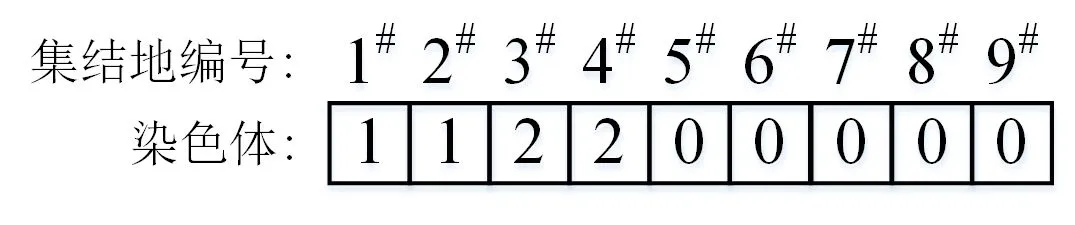
图1 染色体表达式Fig.1 Chromosome expression

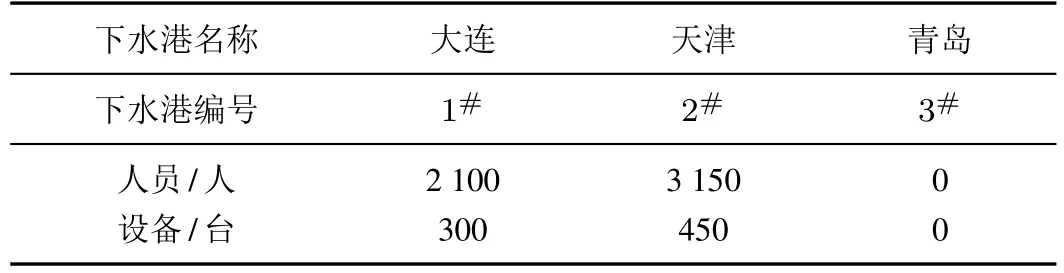
表4 各下水港的人员和装备数量Table 4 The number of personnel and equipment in each launching port

表5 各集结地的人员和装备数量Table 5 The number of personnel and equipment in each staging area

2)适值函数

对于遗传算法得到的每条染色体,其适值函数定义为

其中Cmax是一个较大的正数,它保证适应度非负;适应度越大,其保留下来的概率就越高.

3)交叉和变异

在交叉操作中,首先对父代的染色体进行两两配对,然后通过计算机随机产生交叉位进行交叉,得到新的染色体,如图2 所示.在变异操作中,采用换位变异的方法,即通过计算机随机产生两个基因索引值,然后互换这两个索引值位置上的基因,如图3 所示.

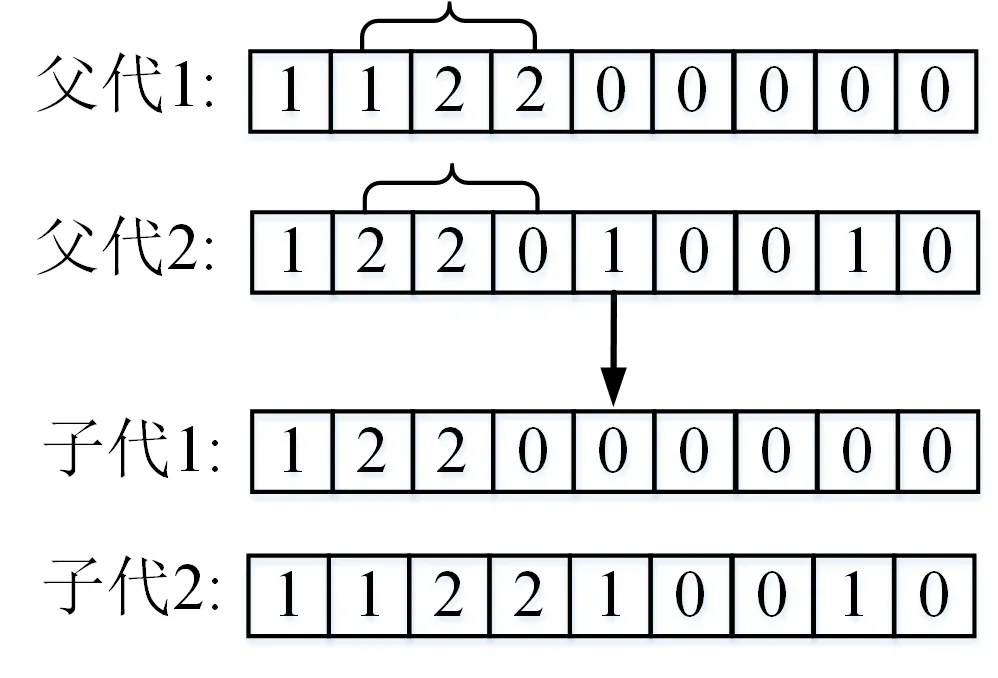
图2 染色体交叉Fig.2 Chromosome crossing

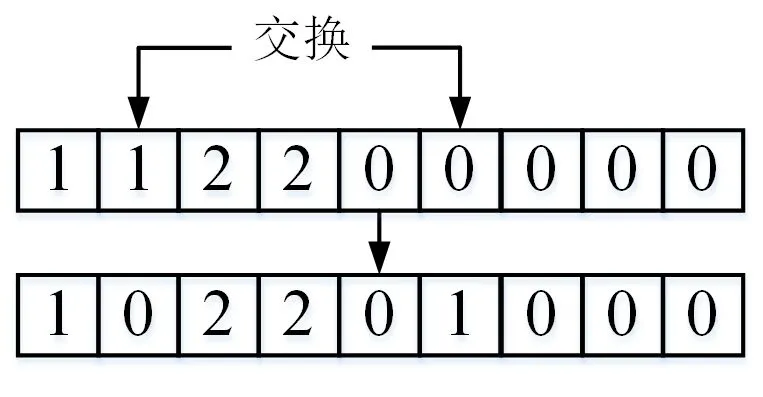
图3 染色体变异Fig.3 Chromosomal variation

3.2 基于路径优化的禁忌搜索算法设计

根据上文分析, 海上运输和铁路运输的优化包括船舶(专列)的航(班)次数量、各航(班)次路线、各航(班)次承载的人数和装备数量等多项内容,解空间十分复杂.本文采取在得到禁忌搜索算法的1 个解时,利用仿真过程来计算该解所对应的海上运输及铁路运输的时间,将其作为禁忌搜索算法中解的评价标准.

使用遗传算法得到的染色体中选择的下水港编号及使用专列运输的集结地编号作为禁忌搜索算法的初始解,为区分下水港和集结地,在该染色体中间添加0 以表示分割.图1 中染色体表示的禁忌搜索算法的初始解如图4 所示,该染色体表示海上运输过程中选择下水港的优先级排序为1>2,铁路运输过程中选择集结地的优先级为5>6>7>8>9.

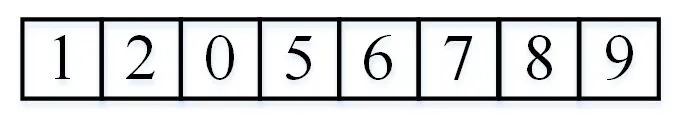
图4 初始解Fig.4 Initial solution

由于传统的禁忌搜索算法难以满足本文的模型,因此需要对算法嵌入计算运输时间的仿真过程,更改传统的邻域操作为分隔邻域操作等几个方面进行改进,具体如下.

1)仿真过程

根据解的表示信息以及约束条件(12)至约束条件(21),对船舶各航次的挂靠港、挂靠顺序、装船量以及专列各班量以及专列各班次经过的集结地、行驶路线和装车量等进行仿真,得出该解所对应的运输时间,具体过程为:

(a)按照当前解所表达的优先级,对有关船舶(专列)先选择优先级较高的下水港(集结地);

(b)在不超过船舶和铁路专列最大装载量的前提下尽可能满载,但如果人员和装备中的有一项达到满载,则船舶和铁路专列则应出发进入启运.

计算运行时,需要对解不断进行评价,以便在迭代过程中不断获得质量更优的解.具体做法是随时判断所寻求的运输路径方案是否满足问题的约束条件,同时计算出该方案的运输时间,在满足问题约束条件的前提下得到的运输时间越短,解的质量越高.

2)分隔邻域操作

由于本文设计的内层禁忌搜索算法的初始解与外层遗传算法所传入的染色体有关,而传统的邻域操作方式会将解中的下水港和集结地之间进行交换,有可能改变解的信息结构,因此需将传统的邻域操作方法改成分隔邻域操作,使得下水港之间以及集结地之间的交换相互独立.例如,对于S=12056789 的解,随机产生的结果为第1 位基因与第2 位基因进行交换和第5 位基因与第7 位基因进行交换,实施交换后可得到原解的一个“邻居”S′=21058769,具体步骤见图5

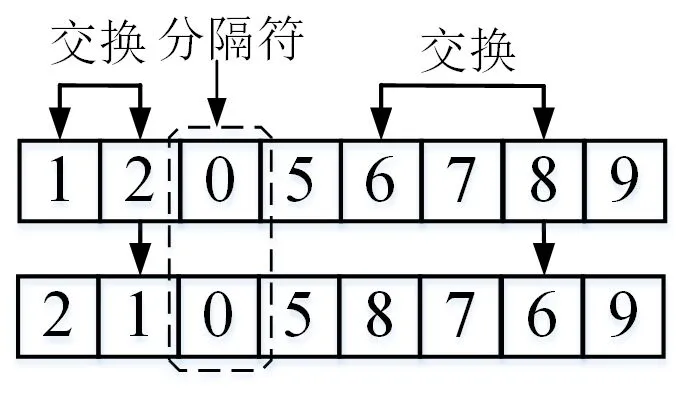
图5 分隔邻域操作Fig.5 Separate neighborhood operation

3.3 计算步骤

步骤1根据遗传算法染色体所表达的信息,生成禁忌搜索算法的初始可行解x0;

步骤2选取初始可行解x0和禁忌表H,记当前最优解为xbest=x0;

步骤3根据得到的可行解,按照仿真原则和约束条件对船舶的航次数量、各航次挂靠港、挂靠顺序、装船量等信息及专列的班次数量、各班次中转站、各班次行驶路线和装车量等信息进行仿真计算;

步骤4根据仿真结果,计算船舶运输时间和专列运输时间;

步骤5若此时已满足禁忌搜索算法终止条件,停止计算,输出最优解所对应的船舶航次数量、各航次挂靠港、挂靠顺序、装船量及专列的班次数量、各班次行驶路线和装车量,进入下一步.否则,在xbest的邻域N(xbest)中选取满足禁忌表要求的可行解作为候选集N′(xbest),在候选集N′(xbest)中选择一个总运输时间最短的解x1,令xbest=x1,更新禁忌表H,返回步骤3;

步骤6将计算得到的船舶运输时间和铁路专列运输时间中的最大值作为当前解的适应值返回给遗传算法框架;

步骤7若此时已满足遗传算法终止条件,停止计算,进入下一步.否则,重新进行选择、交叉、变异生成新一代种群,然后返回步骤1;

步骤8结束.

4 实例分析

4.1 背景及数据

现以从我国北部、中部和东部战区各集结地利用海铁协同并进的运输方式向东海前线的宁波市进行战略投送为例,其集结地为长春等9 个地区,根据上级要求,需投送的人员和装备的数量见表6.

表6 各集结地待运输的人员和装备数量Table 6 The number of personnel and equipment to be transported in each staging area

假设集结人员和装备的时间为3 d,陆上行进的速度平均为60 km/h;大连港、天津港和青岛港可作为下水港供方案优化时选择;已调集3 艘船舶(以下简记为船舶1#、船舶2#和船舶3#)及三列专列(以下简记专列1#、专列2#和专列3#).船舶的出发地均为大连港,船舶承载能力为人员1 400 人,装备200 台,人员上下船的速度为1 min/人,装备装卸的速度为10 min/台; 考虑到天气的影响,船舶的平均航速设为16 节,如遇到不利天气耽搁,可适当提高船舶航行速度以满足计划船期;船舶航行前的安全检查需2 小时,靠离泊作业各需1 h.专列的承载能力为人员500 人, 装备80 台, 人员上下车的速度为10 s/人, 装备装卸的速度为10 min/台,平均速度60 km/h;专列出行前的安全检查需1 h,其他有关计算的参数如表7 至表9.

表7 陆上各集结地至下水港之间的距离/kmTable 7 The distance between land staging areas and launching ports/km

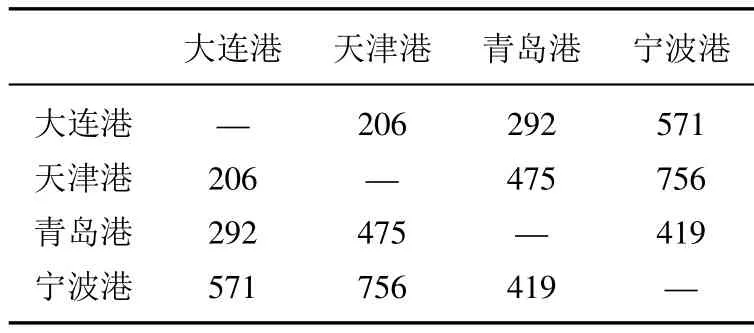
表8 各港口之间的海上距离/n mileTable 8 Maritime distance between ports/n mile

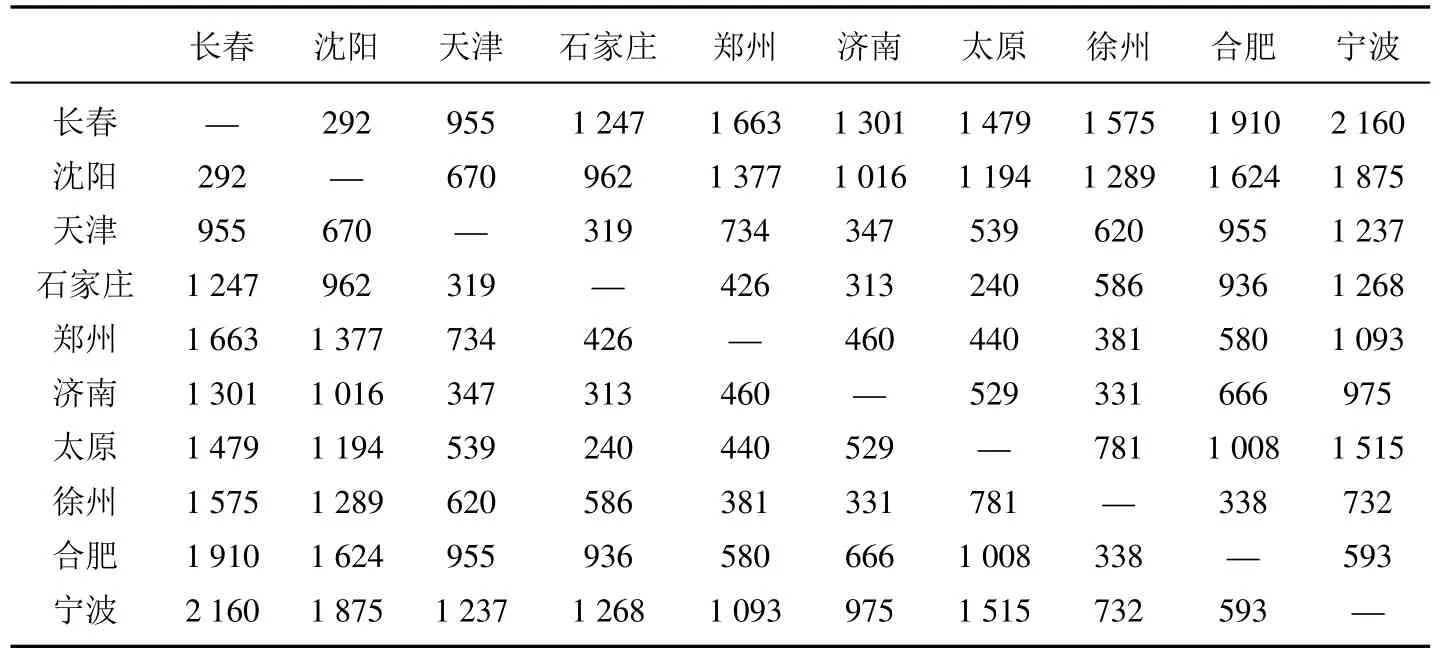
表9 各城市之间的陆上距离/kmTable 9 Land distance between cities/km

4.2 计算结果及分析

本文使用Python 语言编程,选用处理器为inter(R)i7-8750H,内存为8G 的计算机计算.遗传算法种群规模选为100,交叉概率0.7,变异概率0.02;禁忌搜索算法迭代次数为10 次,候选集个数为5,禁忌表长度为5.经计算得到完成全部投送任务共需24.14 d,运输方案为从长春和沈阳出发的选择由大连港出海;从天津和石家庄出发的由天津港出海;从济南和徐州出发的由青岛港出海;从郑州、太原和合肥出发的选择由铁路专列运输.

海上船舶运输的方案优化为:编号为1#船舶在第1 个航次从大连港承载1 400 人和200 台装备运到宁波港;其第2 个航次返回青岛港承载1 400 人和200 台装备再运到宁波港;编号为2#船舶在第1 个航次先从大连港承载700 人和100 台装备,然后再从天津港承载700 人和100 台装备运抵目的地宁波港;此后的第2 个航次则从青岛港承载700 人和100 台装备再运抵宁波港;编号为3#船舶从大连港空载出发到天津港承载1400 人和200 台装备后再运到宁波港(表10 和表11).

表10 下水港选择方案Table 10 Launching port selection plan

表11 铁路运输方案Table 11 Railway transportation plan

专列的运输方案为:专列1#的第1 个班次从太原承载500 人和80 台装备后行驶至宁波;第2 个班次从郑州承载500 人和80 台装备后行驶至宁波;第3 个班次从郑州承载150 人,中转合肥承载350 人和80 台装备后行驶至宁波;专列2#的第1 个班次从太原承载500 人和80 台装备后行驶至宁波;第2 个班次从郑州承载500 人和80 台装备后行驶至宁波;第3 个班次从合肥承载350 人和20 台装备后行驶至宁波;专列3#第1 个班次从太原承载400 人和40 台装备,中转郑州承载100 人和40 台装备后行驶至宁波;第2 个班次从郑州承载500 人和50 台装备后行驶至宁波(表10 和表12),运输路线如图6 所示,计算收敛过程如图7 所示.

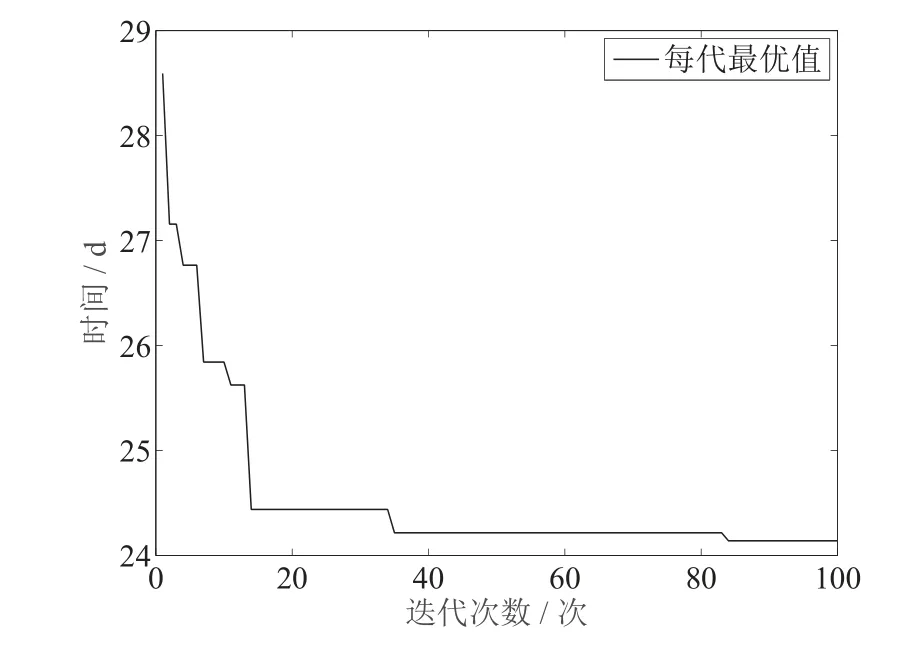
图7 本文算法运行过程性态示意图Fig.7 Schematic diagram of the running process of the algorithm

表12 海上运输方案Table 12 Maritime transportation plan

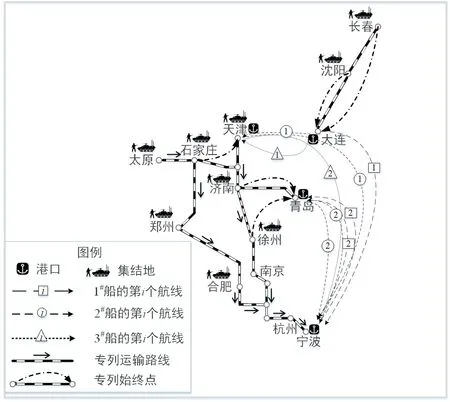
图6 东海战略投送运输图Fig.6 Strategic delivery map for the East China Sea

4.3 算法比较

本文用模拟退火算法(SA)及遗传算法(GA)的计算结果与本文算法(GTSA)进行对比, 其中模拟退火算法初始温度为1 000 度,蒙特卡洛内部循环为50 次; 遗传算法种群规模为100,交叉概率为0.7,变异概率为0.02.另外,为了进行敏感性分析,本文采用四个不同的算例规模分别计算10 次,设N=1 即为4.1 节的基本数据,N=2 时,将人员和装备数量均增加至2 倍,以此类推.测试环境均在处理器为inter(R)i7-8750H,内存为8G 的计算机上进行.结果显示, 在4 组算例中, 本文算法相对于模拟退火算法和遗传算法在运行时间上分别减少了4.96%～16.44% 和12.31%～20.39%; 在优化结果上分别改善了7.65%～10.48%和1.44%～6.14%;在算法稳定性上分别提高了50.74%～95.94 ˙%和5.33%～89.07%.在不同计算规模上,本文算法在计算时间、优化结果和计算稳定性等各方面均优于模拟退火算法和遗传算法.算法对比结果列于表13,其中不同规模下GTSA 与GA 的收敛曲线见图8.

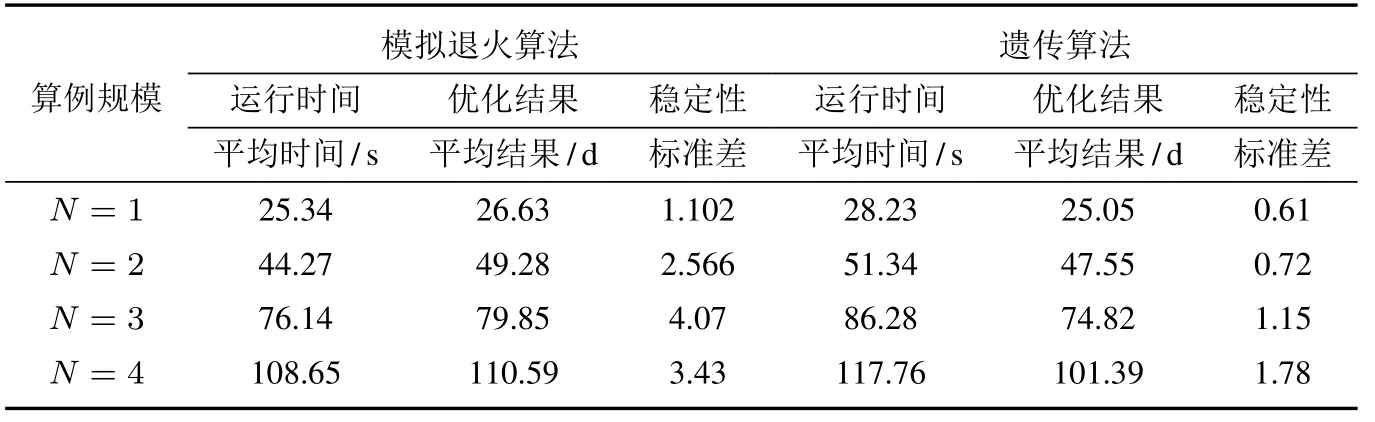
表13 不同算法结果对比Table 13 Comparison of different algorithms

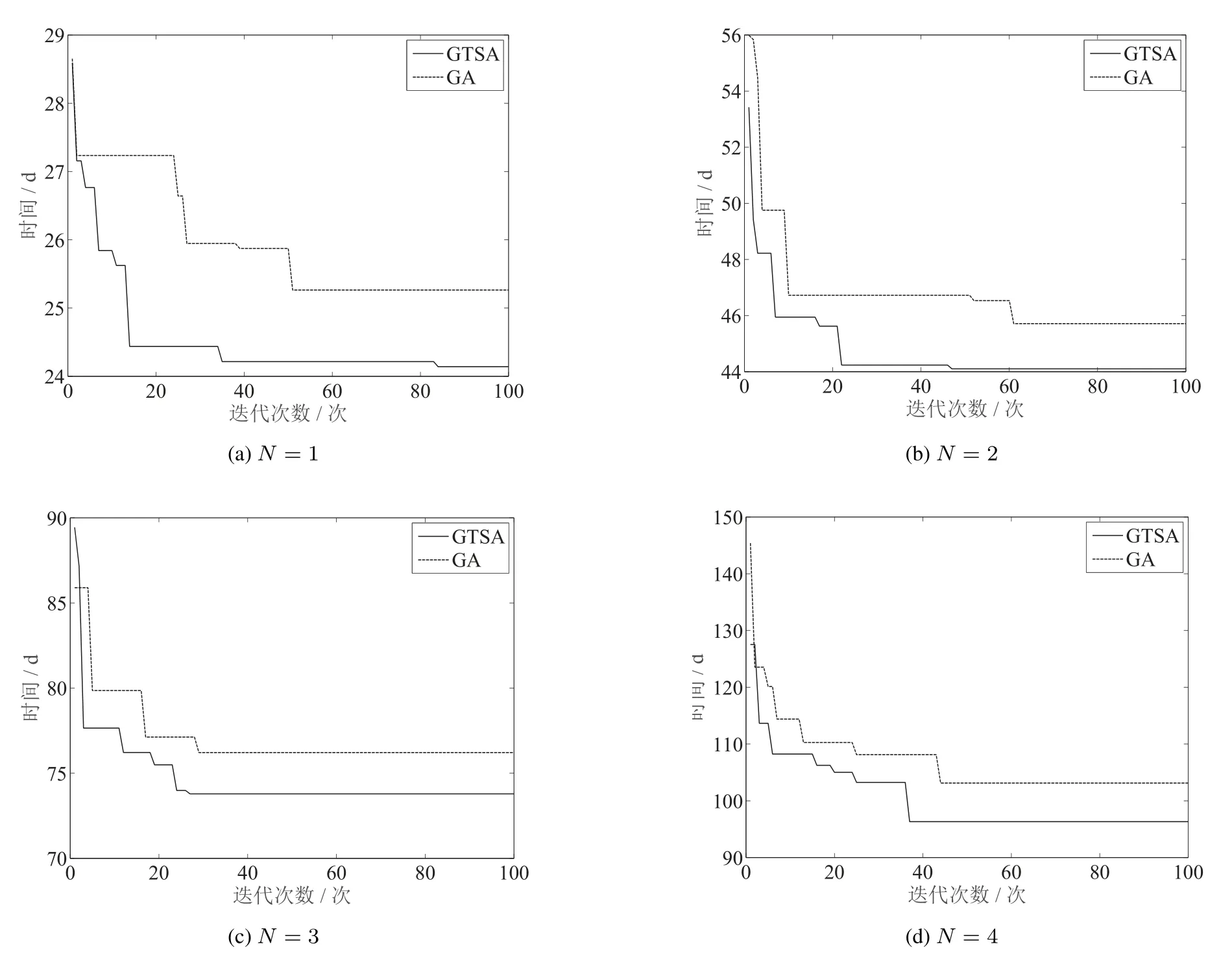
图8 不同规模下GA 与GTSA 收敛对比图Fig.8 Comparison of GA and GTSA convergence at different scales

此外,为进一步验证本文算法的有效性,将文中实例的数据带入CPLEX 软件进行求解.结果显示,当集结地及下水港的数量不变,仅增加投送规模时,本文算法求解的精度略低于CPLEX 的结果,但求解速度远快于上述软件(表14).进一步地,当集结地及下水港的数量增多时,上述软件的运行便发生困难,以至于难以求出最优解,而本文算法则仍可以在较短的时间内完成计算.

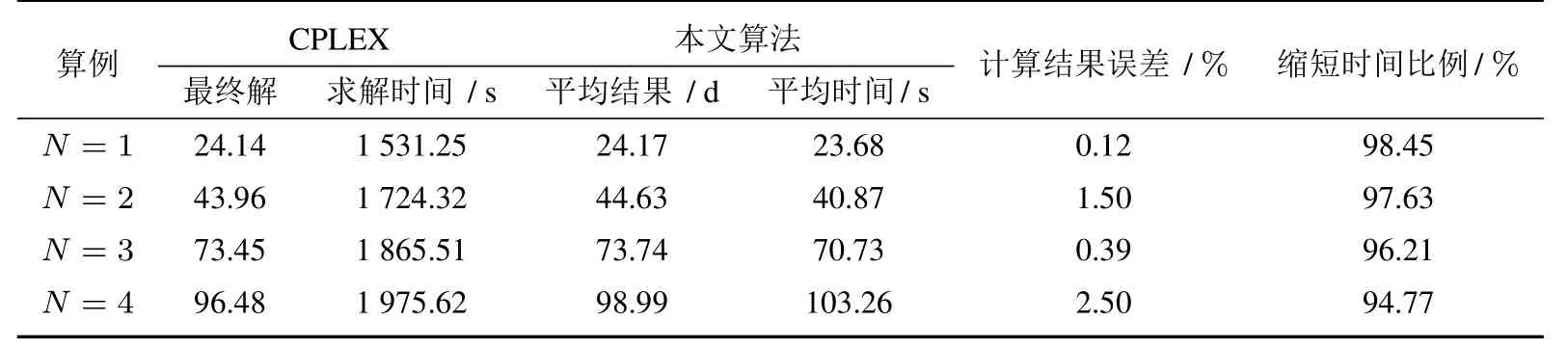
表14 本文算法与CPLEX对比结果Table 14 Comparison of the algorithm and CPLEX

续表13Table 13 Cotinues

5 结束语

与传统的LRP 问题相比,海铁协同并进的战略投送需解决运输方式和下水港的选择、船舶运输路线优化和专列运输路线优化等问题,其中混合着船舶的装船量、专列的装车量等约束条件,因而使得海铁协同并进的求解更为复杂.

为更有效地求解上述问题,本文以遗传算法解决运输方式和下水港选择问题;以禁忌搜索算法优化船舶和铁路专列的运输路线问题;利用仿真分别计算海上运输时间和陆上运输时间,通过内外层之间的协同优化,最终求得优化后的方案.最后,以我国向东海地区战略投送为例,得到运输时间最短的运输方案,说明以本文模型和算法求解此类问题是合理且有效的.通过与其他算法进行对比以及灵敏度分析,显示出本文算法在不同规模中均能在更短的时间内得到更优质的解,且具有更好的稳定.

需要指出的是,本文模型主要解决在正常约束条件下的战略投送问题,而在紧急情况下,由于军情是压倒一切的,实际中如需要可对部分道路、桥梁、车站、码头等交通设施实施军事管制,此时已有的常规性交通法规等约束将暂时失效,船舶和专列的调用将大大加快,相应的优化模型也将调整,如何解决此类问题是下一步的研究内容.