采出液温度对油水旋流分离器内流场及分离性能的影响

刘 冰，吴 震，高 群，谢 超，赵振江，李 栋，薛建良

(1.山东科技大学机械电子工程学院，山东 青岛 266590；2.山东科技大学安全与环境工程学院)

在原油开采、集输、炼制、加工等过程[1-2]中会产生大量含油废水，其成分复杂、可降解性差、有毒有害，因而处理难度较大[3]。对于油田采出废水，常用的处理方法有重力沉降分离、气浮处理、离心处理、膜分离处理，以及多种技术组合处理等[4-5]。其中，离心处理方法具有高效且简便的特点，是一种较为理想的选择[6]。油水旋流分离器(简称旋流器)是离心处理工艺的典型设备，被广泛用于含油废水的油水分离，其分离性能主要取决于其几何参数和操作参数[7-8]。

操作参数对旋流器分离性能的影响是不容忽视的[9]。Liu Bing等[10-11]讨论了旋流器入口流体速率与气液比(GRL，旋流器入口流体中空气所占体积分数，下同)之间的耦合关系，发现当入口流体速率为4～10 m/s、气液比为30%～40%时，旋流器的分离性能最佳。而Li Fing等[12]研究了旋流器入口流体速率与入口流体中油相体积分数对其分离性能的影响，发现入口流体速率为5～8 m/s、入口流体中油相体积分数为1%～9%时，旋流器的分离效率最高。王华健等[13]发现破胶程度降低会减少旋流器能量损耗，但同时也会降低其分离效率；马猛等[14]研究高含水稠油采出液黏度变化对旋流器分离性能的影响，发现导叶型轴向入口分离器对采出液黏度敏感度更小，适用范围更广；徐保蕊等[15]发现采出液黏度对三相旋流器的速度场影响较小，而对压力场影响较大，而合适的采出液黏度会使分离效率达90%以上。

受环境因素影响，含油废水的温度会有所变化，其物理性质也会随之不断变化，进而影响到旋流器分离性能。然而，目前有关含油废水温度对旋流器分离性能影响的研究很少。鉴于此，本课题以油水分离旋流器为研究对象，借助雷诺应力模型与混合模型相结合的数值模拟方法，并结合试验，在10～80 ℃温度范围内考察油水温度对旋流器分离流场、油相分布及分离效率的影响，通过分析旋流器内部流场参数及其分离性能指标，确定油水旋流分离性能最佳的温度范围。

1 数值模拟与实验

1.1 数值模拟模型

1.1.1 几何模型用于数值模拟和试验研究的旋流器为双入口双锥旋流器，其结构示意见图1(a)。其中，x，y，z为坐标方向；O为坐标原点，因旋流器柱段区域为油水分离的主要发生区域，故选取旋流器内流场中z=15 mm处横截面S1作为特征截面。综合考虑油水分离旋流器的几何特点、内部流场特性，采用六面体结构划分网格[16]，具体划分情况如图1(b)所示。

图1 双入口旋流器的几何模型与网格划分示意

1.1.2 数学模型考虑到旋流器内部流场是一个复杂的强各向异性旋转湍流多相系统，数值模拟选用雷诺应力模型(RSM)和混合模型(Mixture model)。RSM可以高精度求解各输运方程，适用于旋流器内各向异性的湍流流动模拟，其控制方程如式(1)所示[10-12]。

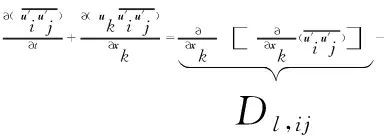
(1)

Mixture模型通过求解混合相的连续性、动量、能量以及第二相体积分数方程，模拟有较强耦合的两相流及相间流动，其连续性方程如式(2)所示[17-18]。

(2)

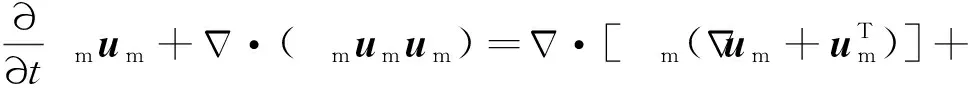
(3)

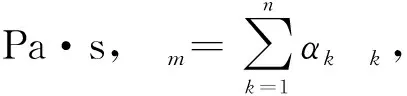
(4)

式中：Ek指k相所含有的能量，J；p表示k相压力，Pa；keff代表有效热传导系数；SE指所有含有的体积热源，J；T为温度，℃。由Mixture模型的连续性方程推得的第二相体积分数方程见式(5)。

(5)

1.2 模拟参数设置

混合模型中设水相为主相，油相为次相，次相以球形粒子的形式分散于主相中，其直径为1×10-5m。考虑到相间相互作用，采用Shciller-Naumann曳力模型，其中曳力因子采用Brucato模型；主次相碰撞恢复系数为0.9；滑移速度模型选用Manninen-at-al模型；主/次相表面张力系数设为0.041 6 N/m。设置入口边界条件为“速度入口”，主、次相均沿入口截面法线方向以10 m/s的初始速度进入旋流器，溢流和底流出口均设置为自由出口。离散相方程采用QUICK差分格式，压力-速度的耦合采用SIMPLE算法，设置壁面为绝热和无滑移条件。模拟介质为特定温度下油相体积分数为3%的油水混合物。

将旋流器按不同网格数(4.8×105，5.4×105，6.5×105，7.8×105)进行划分，并以旋流器S1截面上分离流场中油水混合物的切向速度(vt)为检验指标进行模拟对比，结果如图2所示。由图2可知，当网格数目超过6.5×105后，网格数目再增加，vt数值较接近、变化幅值不超过0.1%，表明数值模拟结果并不依赖于网格数量而存在[18-19]。因此，数值模拟选用的网格数为6.5×105。

图2 网格无关性验证■—4.8×105； ●—5.4×105； ▲—6.5×105；

1.3 模拟可靠性验证试验

模拟结果可靠性验证试验系统如图3所示。试验系统主要由油田采出液存储罐、净化水存储罐、分离油存储罐、油水混合搅拌器、旋流器、液体泵，温度计、流量计、压力计、开关等组成，均由耐压管路连接。

图3 油水分离试验系统示意

试验用油水混合物为油田采出液，由胜利油田提供；经预处理后，采出液经1号泵进入混合搅拌器混合、加热；达到预设温度后，经2号泵进入旋流器进行分离净化。分离后的油相从溢流口排至分离油存储罐，水相从底流口排至净化水存储罐。试验时，调整2号泵的功率，使旋流器入口采出液流速恰好达到10 m/s。由采样点A取样，测定旋流器入口的采出液中油相体积分数，同时读出入口压力(pi)和油水混合物入口流量(Qi)；待旋流器正常工作且处于稳定状态时，分别从取样点B、C取样，测定流经旋流器溢流口和底流口的油水混合物流体中油相体积分数，同时分别读取溢流口处的压力(po)和油水混合物流量(Qo)和底流口处的压力(pu)和油水混合物流量(Qu)。

对旋流器溢流分流比和压降比的模拟值和试验值进行分析，结果见图4。其中，溢流分流比(简称溢流比)为Qo/Qi；而压降比(PDR)[18-19]的计算如式(6)所示。

图4 试验验证结果溢流比，%：▲—模拟值； ■—试验值。PDR：模拟值； ●—试验值

(6)

式中，Δp1、Δp2分别指溢流压降和底流压降，MPa。

由图4比较旋流器溢流比的模拟值与试验值可知，在研究温度范围内其模拟值与试验值均随温度升高而增大，二者最大误差为2.54%，因而可认为在误差允许范围内旋流器溢流比的模拟值与试验值吻合。比较旋流器压降比的模拟值与试验值发现，PDR的模拟值与试验值相近，二者最大误差为2.13%，因而可以认为PDR的模拟与试验结果相一致。上述研究结果说明在研究温度范围内，数值模拟模型具有较好的适用性，模拟结果可靠。

2 结果与讨论

2.1 速度分析

2.1.1 油水混合物切向速度分离流场中油水混合物的切向速度决定了油水分离离心力的大小，因而比其径向速度、轴向速度更为重要[20]。因此，选取S1截面上的切向速度(vt)，绘制其在不同温度下随径向位置变化规律，如图5所示。由图5可知：vt成对称分布，且服从Rankine涡分布，为半自由涡区和强制涡区的组合[20-22]；温度对S1截面上vt的影响主要体现在半自由涡区域，而在强制涡区域温度对vt的影响较小，具体地说，vt与温度呈现正相关关系，半自由涡区域的vt受温度影响变化增幅最大，而在强制涡区，vt受温度影响变化幅度较小。

图5 不同温度下S1截面切向速度分布温度，℃： —10； —20； —30； —40； —50； —60； —70； —80。图9同

出现上述现象的原因是在半自由涡区域，油水两相的动力黏度随温度的升高而降低，所受黏性阻力减小，切向速度受温度影响而变化幅度增大；而在强制涡区域，因温度升高而使油水混合物的湍流加剧，扰乱因温度升高而产生的切向速度变化，使此区域内油水混合物的切向速度变化较小。

2.1.2 油滴粒子径向沉降速度油水旋流分离过程中，根据旋流器内部组合涡流场规律[20-22]，油滴粒子向轴心处迁移的过程中会受到向心浮力(Fp，N)、离心力(Fc，N)、黏滞阻力(Fs，N)和Magnus力(FM，N)的作用[23]，

其计算式分别如式(7)～式(10)所示。

(7)

(8)

Fs=3πμwdvr

(9)

FM=αρwd3ω×vr

(10)

式中：dp/dr为径向压力梯度，Pa/m；d为油滴粒子直径，m；r为径向位移，m；μw为连续相的动力黏度，Pa·s；vr为油滴粒子的径向沉降速度，m/s；α为比例系数；ω为油滴旋转的角速度，rad/s。

其中，Fp是油滴粒子迁移的主要动力，而Fc和Fs是阻力，FM的方向随着油滴粒子旋转方向的变化而变化[23]。由于FM数值较小而通常略去[23]，故对油滴粒子径向受力分析如图6所示。

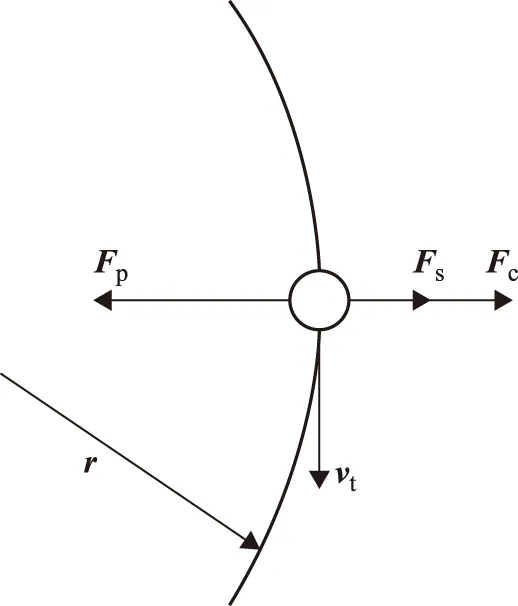
图6 油滴粒子径向受力分析

油滴粒子受力平衡方程如式(11)所示。

(11)

当旋流器内流场处于相对稳定时，油滴粒子沿径向作等速运动(即dvr/dt=0)，其所受力Fp，Fc，Fs达到平衡，油滴粒子的vr可用式(12)计算。

(12)

油滴粒子的径向沉降速度分布如图7所示。由图7可知：油滴粒子的径向沉降速度成对称分布；随着温度升高，油滴粒子沉降速度从旋流器的柱段向锥段沿中心轴线递增，其径向沉降速度零值区域(图中蓝色区域)逐渐增大；随着温度升高，中心轴线处油滴粒子径向沉降速度由最初的1.2 m/s增加至1.8 m/s，表明油滴粒子在流场中运动趋于稳定时，随温度的升高会增加其在轴心处的聚集率，从而提高油水分离性能。

图7 油滴粒子径向沉降速度分布

由式(12)可知：油滴粒子径向沉降速度与油水混合物切向速度的平方成正比关系；随着温度升高，vr的增幅远大于vt的增幅；正是在逐渐增大的径向沉降速度的作用下，油相粒子的体积分布更加集中。

2.2 压力分布

分离流场中油水混合物的压力分布不仅影响其分离性能，而且决定了分离系统的运行成本[22]。图8为不同温度下的分离流场中油水混合物压力分布云图；图9为不同温度下分离流场中S1截面上油水混合物的压力分布。由图8可以发现，随着温度升高，轴心两侧油水混合物的压力呈现明显增大趋势，而轴心区域因强旋流而形成负压，其数值随温度升高有减小的趋势，且油水混合物的最低负压位置随温度的升高而沿其轴向升高(图中蓝色线所示)，这为聚集在轴心处的油滴自溢流口排出提供了动力，从而使得油水分离效率提升。

图8 分离流场中油水混合物压力分布

从图9可以看出：在半自由涡区，随着温度升高，油水混合物内能增大、动力黏度减小，因黏性阻力等损耗的能量减少，同时油水混合物的机械能相对增加，压力和流速随着温度升高而升高；而在强制涡区，由于温度升高导致径向压降增大，流体在沿径向向轴心运动过程中，因湍流加剧而使其能量损耗增加，导致其动能和压力能相对降低，压力降低，因而油水混合物的最低负压位置随着温度升高而略有升高。

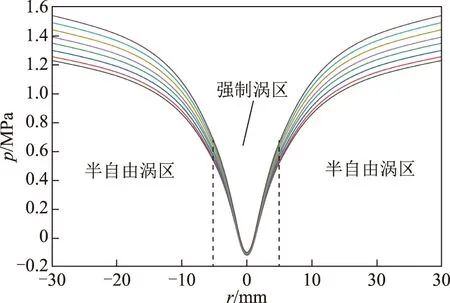
图9 不同温度下旋流器S1截面上油水混合物压力分布

2.3 湍动能分析

吕凤霞等[24]和邢雷等[25]先后对旋流器内部油滴破碎聚集现象进行了细致研究，他们发现湍流加剧会导致旋流器中油滴破碎，甚至乳化。因此有必要研究采出液温度对旋流器内油水混合物湍动能的影响规律。图10为不同温度下S1截面上油水混合物的湍动能分布的八分之一截图的组图。由图10可以看出：由旋流器边界沿径向至中心区域，油水混合物的湍动能由10 m2/s2逐渐增加至40 m2/s2；随着温度升高，旋流器轴心处流体高湍动能(红色区域)面积逐渐扩大，表明油水混合物的湍动能与温度呈现近正相关关系。

图10 旋流器S1截面上油水混合物湍动能分布

产生此规律的原因在于：S1截面轴心处存在较强的涡旋，油水混合物的速度、压力降低，其动能及压力能也减小，速度脉动量增大，流体湍动能增加；温度越高，油水混合物的速度脉动量越大，轴心处流体的湍动能越大；旋流器内部流场的速度、压力、湍动能等因此呈现较强的各向异性。

2.4 油相体积分布

不同温度下旋流器内油相体积分布的数值模拟结果如图11所示。从图11可以看出，油相主要集中于轴心区域，随着温度升高，油相在轴心处的富集程度提高(红色区域)，油相含油体积分数从85.21%上升到99.18%，提高13.97百分点，而旋流器中轴线上油相最低体积分数的位置也随着温度的升高而升高(图中红色虚线)。油、水的动力黏度均随着温度的升高而降低，油滴粒子受到的黏滞阻力降低，油滴粒子相对于连续相径向沉降速度升高，致使油滴粒子可以容易地穿过连续相而向轴心迁移，随着迁移到轴心附近的油滴粒子数目增多而使得油相富集程度升高。

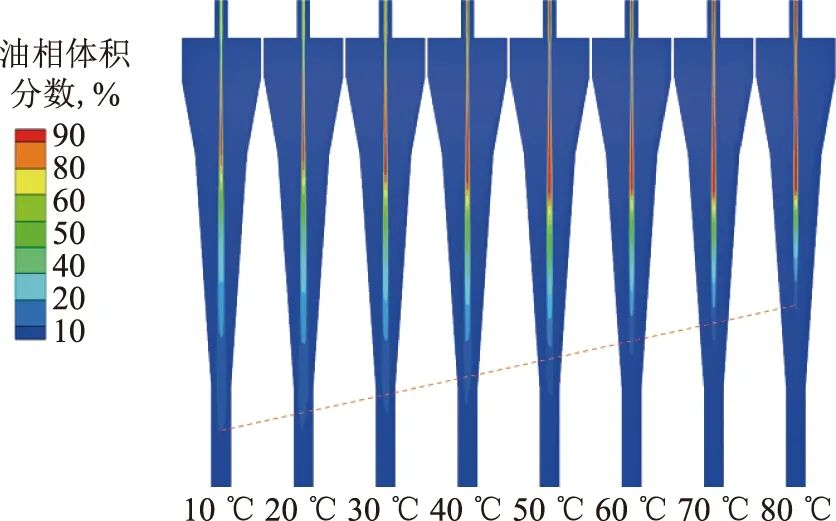
图11 不同温度下旋流器内油相体积分布

以油相体积分数不低于10%的油芯为研究对象，采用油相体积分布非均匀度来量化其体积分布的非均匀性，其计算式如式(13)所示。

(13)

式中：σ为油相体积分布非均匀度，%；domax和domin分别为油芯的最大直径和最小直径，mm。

图12为油相体积分布非均匀度和油芯平均直径随温度升高的变化曲线。由图12可知：σ与温度成负相关，随着温度的升高，σ从94.36%降至72.58%；随着温度升高，油芯的平均直径(da)减小，从2.94 mm减至2.78 mm，表明随着温度升高油芯分布逐渐均匀，油相逐渐聚集在轴心区域，并在轴向浮力的作用下经溢流口排出。

图12 不同温度下油相体积分布非均匀性及油芯平均直径■—σ； ▲—da

2.5 分离效率

旋流器的分离效率是评价旋流器分离性能的重要指标之一，通常以旋流器的实际分离效率来衡量旋流器的分离能力[16-17]，计算式如式(14)所示。

(14)

式中：E是旋流器的分离效率，%；wu和wi分别为旋流器底流口和入口油水混合物中油相体积分数，%。

旋流器分离效率的模拟值与试验值的对比如图13所示。由图13可知：旋流器分离效率与温度成非线性正相关；随着温度由10 ℃升至80 ℃，旋流器的分离效率由89.13%增至99.06%，增长9.93百分点；试验测得的分离效率与模拟结果基本一致。

图13 不同温度下旋流器分离效率的模拟值与试验值▲—模拟值； ■—试验值

综合分析图10～图13可知：当温度低于70 ℃时，旋流器的分离效率较低，小于99%，且油相分布不集中；当温度高于70 ℃时，油相分布更集中，旋流器的分离效率达99%以上。

3 结 论

基于RSM和Mixture模型，数值模拟了采出液温度对旋流器的分离流场、油相分布和分离效率的影响规律，并进行试验验证，发现：

(1) 旋流器流场中油水混合物的切向速度、压力、湍动能以及油滴粒子的径向沉降速度与温度均成正相关，随着温度升高，油滴粒子的径向沉降速度增大，油滴加速向轴心聚集；轴心处油水混合物的湍动能逐渐增大，最低负压位置升高，油相可顺利由溢流口排出。

(2) 随着温度升高，轴心处流体中油相体积分数提高13.97百分点，油相富集程度增加；油芯直径下降，油相分布更加均匀，有利于油和水的分离。

(3) 旋流器的分离效率与温度成非线性正相关。温度升高，油相分布更集中且分离效率提高；当温度高于70 ℃时，旋流器的分离效率达99%以上。