面向大规模并行的全隐式托卡马克MHD数值模拟*
蒋子超,江俊扬,孙哲,姚清河
1. 中山大学航空航天学院,广东广州 510006
2. 日本理化学研究所,日本东京197-0804
等离子体的MHD 不稳定性是限制托卡马克等磁约束核聚变装置长期稳定运行的主要因素之一。撕裂模等MHD不稳定性的发展容易导致磁面破坏、输运增强,从而导致等离子体的约束退化。因此,探索等离子体不稳定性的抑制手段已经成为目前磁约束核聚变研究中的关键问题之一[1]。
针对托卡马克中的磁流体不稳定性,目前学界多采用基于MHD方程的数值模拟方法进行研究。20 世纪90 年代, Barmin[2]和Nessyahu 等[3]已分别采用逆风格式和二阶精度高分辨率无振荡的中心差分格式求解一维/二维MHD 方程[4]。此后,学界开始尝试对三维托卡马克位形下的等离子体进行数值模拟,但是受制于有限的计算能力,针对托卡马克等离子体的仿真求解器多基于全显或半隐格式,且问题规模和模型精度也较为受限。Harned 和Kerner[5]以及Harned 和Schnack 等[6-7]首先提出了简化代数算子的方法以半隐格式进行求解,近年来经过多次改进与优化[5-7],目前已被广泛应用于MHD仿真计算领域求解器的开发,例如:XTOR[8]和NIMROD[9]。此外,较为成熟的托卡马克磁流体求解器还有M3D[10]、BOUT++[11]等;我国比较成熟的托卡马克等离子体求解器包括浙江大学马志为教授团队开发的CLT[12]/CLT-K[13]求解器。
虽然基于全显式和半隐式的求解器已经取得了许多计算成果,但是基于此开发的求解算法的时间步长严格受限于CFL(courant-friedrichs-lewy)条件。撕裂模等MHD 不稳定性的形成及饱和过程的模拟需要较长的时间跨度(通常大于104个Alfvén 时间),因此全显式和半隐式将导致过多的计算步数,而采用全隐格式则可解除CFL 条件的限制,实现较大时间步长的全局求解。此外,捕捉非理想等离子体不稳定性需要高分辨率网格,但对计算机内存以及计算机求解能力的要求就越严苛,一般的主机和集群无法满足要求。
基于上述因素,本文提出了一种面向大规模并行计算的MHD 方程组的全隐式数值求解方法,对托卡马克等离子体的撕裂模不稳定性进行了数值模拟。本研究以浙江大学马志为教授团队开发的显格式求解器CLT 为参考,采用了与之相同的稳态等离子体物理场数据与几何模型,并基于MPI和并行开源框架PetSc 开发了新型全隐式求解器。本研究在日本理化学研究所(RIKEN)的HOKUSAI 高性能计算平台上完成了对所开发求解器的并行可扩展性测试,并得到了托卡马克等离子体撕裂模的模拟结果。
1 数值模型及算法实现
针对托卡马克等离子体的撕裂模不稳定性,采用带Hall 项的非理想单流体MHD 方程[14-15],并假定等离子体为冷等离子体,即电子压力与流体压力相等,可得speed)vα=Bm(μ0a)1/2,上述参量均可由模型确定。



进一步,将方程(1)中电场和电流密度方程分别代入速度方程与磁场方程,即可消去待解变量E、J得到方程(2),从而减少待求解变量的数目,进而节约存储开销。
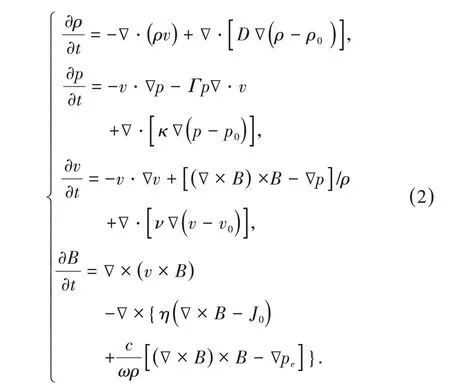
为了研究托卡马克中磁流体动力学效应,可取如图1 所示的几何模型,其中a为截面圆半径,R为截面圆圆心所在的大圆半径,简称环半径。

图1 托卡马克模型Fig.1 Tokamak model
对应的扰动模式,使体系产生不稳定性效应。等离子体处于平衡态时,方程(2)忽略了霍尔效应,且时间导数项为0,可以得到平衡态时的方程。借助专门针对平衡场求解的NOVA 程序[16],对图1所示的模型进行平衡态的求解,其结果可作为模拟等离子体不稳定性的初始分布场。对于图1所示模型中的撕裂模不稳定性,扰动模式如式(3)所示。式中φ为该点环向角,θ为该点的极向角;η0是背景电阻率,在计算过程中为固定值;ψ是磁通量,由具体模型确定;系数-ψ为磁轴位置,在本文算例中均取-0.095 83,系数δ为常数,取0.03。系数m与n确定了扰动模式的类型,如撕裂模对应m/n=2/1,扭曲模对应m/n= 1/1。
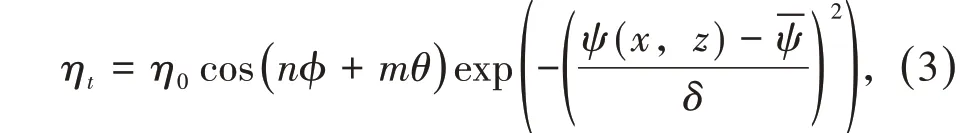
由式(3)可知,扰动模式与时间无关,且服从系数为-ψ与δ的高斯分布。在对方程(2)的实际数值求解过程中,需根据Maxwell 方程组计算出相应的磁场扰动Bp以引入计算,磁场扰动为
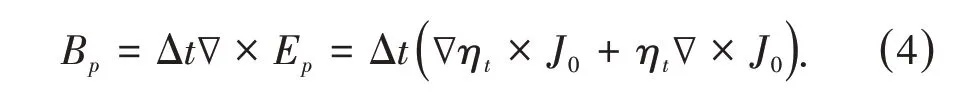
结合方程(2)的数值特性与磁流体不稳定性模拟中对求解精度的要求,本算法采用了全隐式的4阶Crank-Nicholson 格式进行有限差分离散以保证求解的数值精度与稳定性,对于离散后的非线性系统,本文采用了Newton-Krylov 法进行迭代求解,其流程如图2所示。
由图2可知,求解过程以平衡态下的物理场作为求解的初始条件,算法采用了两层嵌套的迭代计算:在每个时间步中,首先根据差分方程计算出雅克比矩阵,然后利用基于并行Krylov子空间的迭代法对所得线性系统进行求解,求得各牛顿步的增量,若该增量小于收敛判据,则推进至下一个时间步的计算。特别地,在计算开始的一定数量的时间步内(在本文中,取计算时间<1τa作为判据),在每个牛顿步收敛后将由式(4)计算的扰动磁场添加至计算结果中,随后进入下一个时间步的循环。

图2 求解器算法流程Fig.2 Algorithm flow of the solver
2 结果分析
为验证本文提出的数值模拟方法与求解器的可靠性,选择m/n= 2/1 的撕裂模算例,取η0=10-5,与CLT 求解器在同模型下的计算结果进行对比,如图3 所示。由图3 可明显观察到磁场的撕裂模不稳定性,本文提出的求解器与CLT 的计算结果在物理场分布上具有较好的一致性。
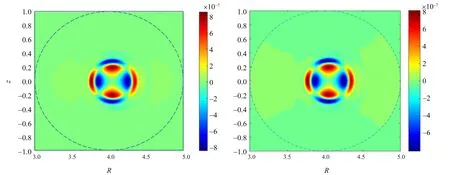
图3 70τa时环向磁场强度计算结果对比Fig.3 Calculation results of circumferential magnetic field strength when 70τa
为进一步验证本文提出算法的精度与结果的网格独立性,分别对同模型下取不同空间步长时的计算结果的相对误差进行校验。由于本物理模型不存在精确的解析解,在如图4所示的精度校验中,本文选用了具有最高空间网格密度的算例作为计算误差的基准算例,并以式(5)进行相对精度阶数的计算,具体误差数据如表1所示。计算误差数据选取环向磁场与环向速度场的计算结果,并以环向空间步长为1/8 时的算例为参考,计算其相对精度阶数。

表1 不同环向空间步长下环向磁场与速度场的相对误差与相对精度阶数Table 1 Relative error and relative accuracy order of Bφ,Vφ under different Δφ
相对精度阶数

式中u*表示网格密度最高的近似精确解。本文以环向空间步长Δφ作为空间网格密度的控制变量,并假设Δφ= 1/64 时的计算结果为近似精确解;可以证明,当趋近于解析解时,由式(5)计算得到的相对精度阶数趋向于实际精度阶数。
由图4 与表1 可知,在该托卡马克磁流体撕裂模不稳定性的算例中,算法表现出良好的网格独立性,且具有近似4阶精度,与算法所采用的差分离散格式的理论精度保持一致。
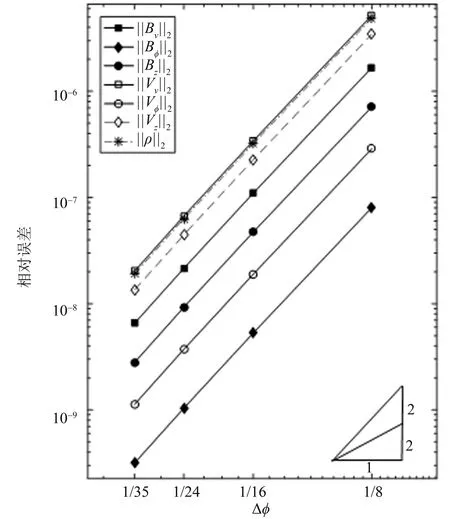
图4 不同环向空间步长下各待解变量的相对误差Fig.4 The relative error of variables under different Δφ
在并行效率与可扩展性方面,使用基于本文提出的求解器进行了测试,测试结果如图5 所示,其中相对加速比根据式(6)计算得到,直接反映了求解器对于计算资源的利用效率,即弱可扩展性。

图5 并行可扩展性测试结果Fig.5 Parallel scalability test results
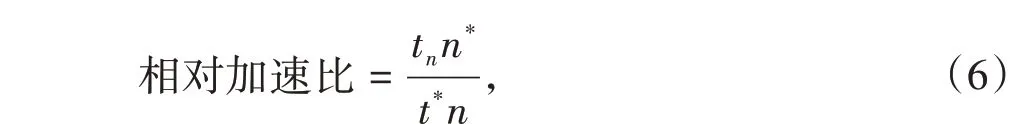
式中t*与n*分别为基准点核心数与计算时间(本测试中,选用160 核心作为基准测试点),tn为核心数为n时的计算时间。
本文采用的测试平台是日本理化学研究所(RIKEN)的HOKUSAI超级计算机,测试中分别对160、320、640、1 280核心下求解器的计算效率进行了测试。表2 中展示了单步求解的平均耗时数据,相对加速比参照式(6)计算。由图5 可知,对于一千核以上级别的大规模并行计算,基于本文提出的算法开发的求解器依然可以保持60%以上的并行效率,由此可见本求解器在实际的大规模磁流体仿真求解中具有较高的使用可行性与参考意义。

表2 100τa内单步求解的平均耗时及相对加速度Table 2 Average time consuming and relative acceleration of single step solution in 100τa
3 结 论
本文基于全隐格式有限差分法及大规模并行模拟提出了一种新型的并行求解MHD方程的算法,并基于该算法对托卡马克装置中的磁流体撕裂模不稳定性进行了验证性的仿真模拟,结果与基于全显格式开发的CLT求解器吻合良好。
在并行效率方面,求解器在HOKUSAI 高性能计算平台上进行了可扩展性测试,结果表明:该算法对于跨节点的并行平台具有良好的并行效率与可扩展性,可适用于大规模并行求解。这对于进一步研究更高精度格式与更接近真实托卡马克装置模型的仿真计算具有重要的参考意义。

