基于因子分析的供电营业厅评价与应用
王波,罗杨,王亮,胡静蕾
(1.国网宁夏电力有限公司吴忠供电公司,宁夏 吴忠 751100;2.国网宁夏电力有限公司,宁夏 银川 750001;3.济南银华信息技术有限公司,宁夏 银川 750001)
0 引 言
目前,利用因子分析进行综合分析评价的研究很多:杨帆[1]等建立的供电营业厅运营效率[2-3]模型实现了对营业厅整体服务资源[4]及运营效率的评估;王磊[5]等针对电能质量综合评估的特点,采用因子分析方法,提出了基于因子分析法的电能质量综合评估模型;宋新甫[6]等基于主成分分析法将电网精准投资影响因素进行降维分析,得到新的综合影响因素。本文构建基于主成分、因子分析法建立的综合分析评价模型,其评价结果能客观地评估营业厅的综合业务水平。
1 评价分析方法
1.1 主成分分析
主成分分析过程是一种数学降维的过程,从多个原始变量中提取出几个综合变量,并且这几个综合变量能够涵盖原始变量的绝大多数信息,且彼此之间没有相关性。
假设有n个样品,每个样品有p项指标,即X1,X2,…,Xp,这p个指标构成的p维随机向量记为X=(X1,X2,…,XP),得到如下原始数据矩阵:
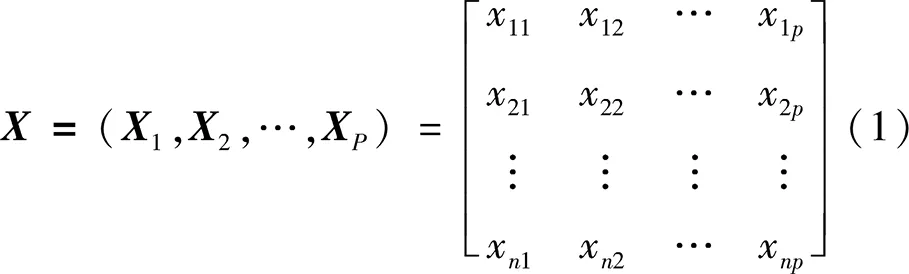
主成分分析就是将p个观测变量综合成为p个新的综合变量的过程,即:
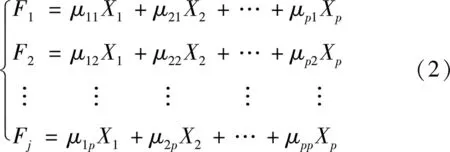
简化为Fj=aj1x1+aj2x2+…+ajpxp。
式中:j=1,2,……p。
式(2)要求模型满足以下条件:
①Fi,Fj互不相关(i≠j,i,j=1,2,…,p)
②F1的方差大于F2的方差大于F3的方差,依次类推。
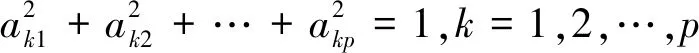
F1为第一主成分,F2为第二主成分,依此类推,Fp为第p个主成分。
1.2 因子分析
因子分析是主成分分析的一种延伸和应用,利用降维的思想研究原始变量相关矩阵内部的依赖关系,把一些错综复杂的变量归结为少数综合因子的统计分析方法。
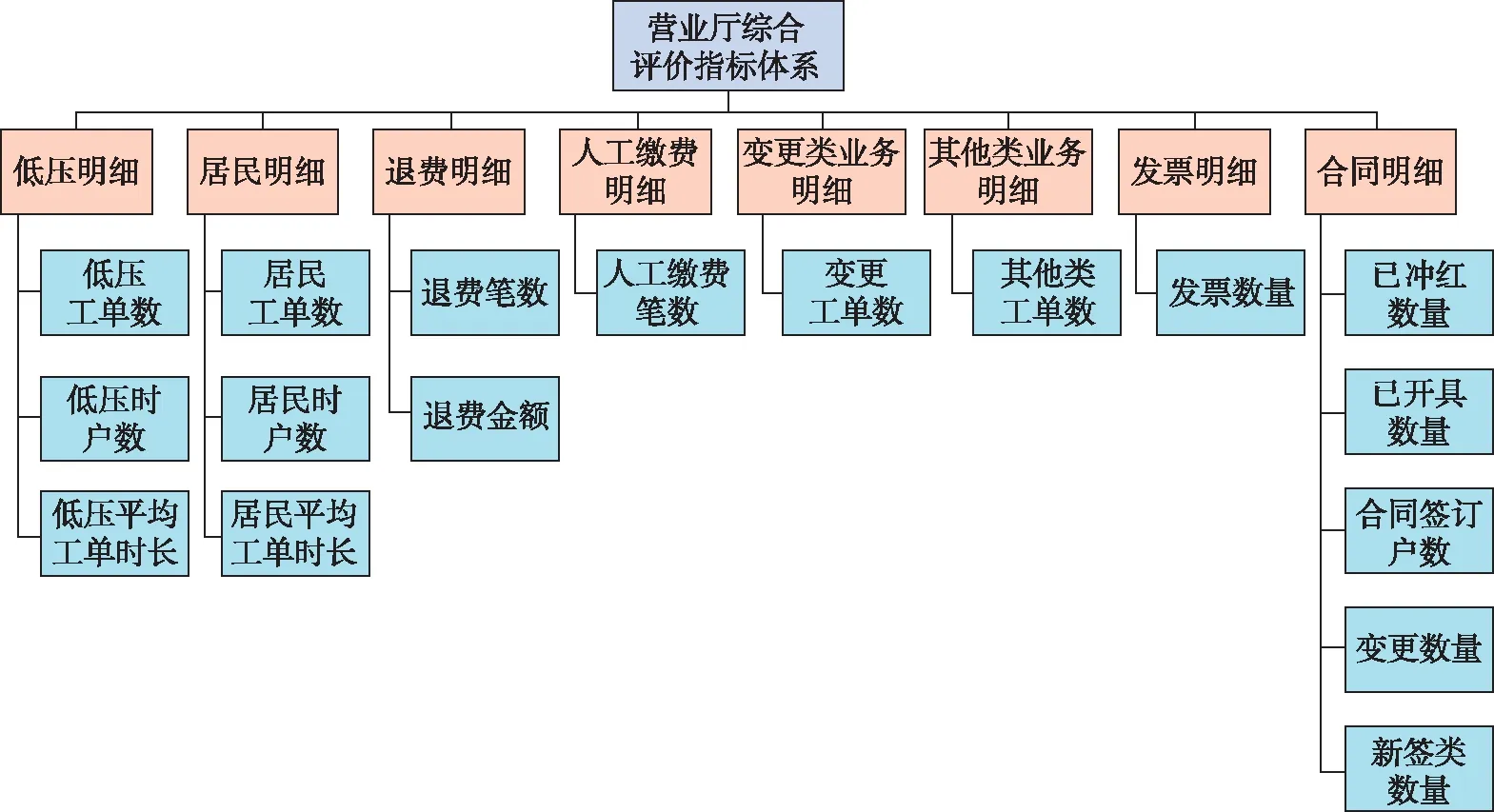
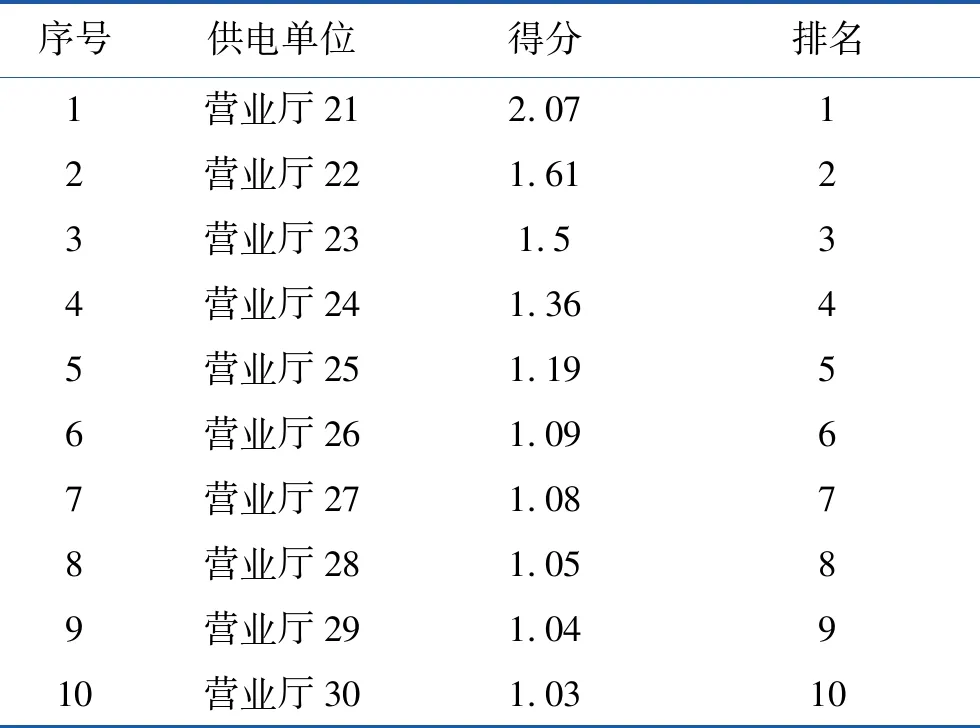
假设有n个样品,p个指标,要求所选取的p个指标间有很强的相关性。将样本观测值构成的数据阵进行标准化处理,数据阵标准化后的矩阵均用X表示,用C1,C2,…,Cm(m 1)X=(X1,X2,…,Xp)T是可观测随机向量,且E(X)=0,协方差矩阵S=cov(X),并且协差阵S与相关阵R相等; 2)C=(C1,C2,…,Cm)T(m ε=(ε1,ε2,…,εp)与W相互独立,E(ε)=0,ε的协方差矩阵Sε是对角阵: 即ε的各分量之间也是相互独立的。 则式(4)成为因子模型: 由模型及其假设前提可知,公共因子C1,C2,…,Cm(m 以营业厅前台人员优化调配为目标,依据跨行业数据挖掘标准流程(cross-industry standard process for data mining,CRISP-DM)数据分析方法论,以电力营销业务系统[7]营业厅线上7类业务17项指标数据为基础数据,构建营业厅分析评价指标体系,如图1所示。 2.2.1 选择指标数据并进行标准化处理 (5) 图1 营业厅综合评价指标体系 2.2.2 充分性与相关性检验 在做主成分、因子分析前要判断他们之间是否有较强相关性,如果指标彼此互相独立或相关性较小,则无法从中提取公共因子,判断能否进行主成分、因子分析的检验是KMO(Kaiser-Meyer-Olkin)检验[8]和Bartlett(巴特利)球体检验[8]。 KMO检验是Kaiser,Meyer和Olkin提出的抽样适合性检验,是对原始变量之间的简相关系数和偏相关系数的相对大小进行检验,取值在0~1之间,值越接近1,变量间相关性越强,偏相关性越弱,因子分析效果越好。计算公式为 (6) 式中:E—KMO检验; 巴特利球体检验主要用于检验相关阵中各变量间的相关性是否为单位阵,即检验各个变量是否各自独立。 (7) R—全体的均方误差MSE。 2.2.3 确定因子个数 因子个数的确定可以根据因子方差和累计方差贡献率来决定,只取方差大于1(或特征值大于1)的因子,按照因子的累计方差贡献率来确定,一般要达到60%才能符合要求。 2.2.4 计算因子得分和综合排名 利用最大方差旋转法对上一步中提出的公共因子进行旋转,使得各因子的方差差异达到最大,并计算公因子得分。 因子总得分=因子1×权重1+因子2×权重2+…+因子n×权重n 式中的权重计算方法,通常可以理解为已经提取的各因子的方差贡献率占累积方差贡献率的百分比,即累计方差占比。 本文使用Python分析工具,用factor_analyzer包进行主成分、因子分析。分析前,先对采集到的17类原始指标数据进行标准化处理,这17类指标分别为X1-低压工单数,X2-低压时户数,X3-低压平均工单时长,X4-居民工单数,X5-居民时户数,X6-居民平均工单时长,X7-退费笔数,X8-退费金额,X9-人工缴费笔数,X10-变更工单数,X11-其他类工单数,X12-发票数量,X13-已冲红数量,X14-已开具数量,X15-合同签订户数,X16-变更数量,X17-新签类数量。标准化处理部分结果如表1所示。 表1 数据标准化处理部分结果 3.2.1 充分性与相关性检验 经KMO检验,值为0.622,大于0.5;经巴特利球形度检验值p(Sig值)为0,拒绝原假设,因此适合做主成分及因子分析。 3.2.2 获取公共因子 这一步用主成分分析法来绘制碎石图,求解特征值,碎石图的横坐标指的是因子数量,纵坐标为因子特征值(可以理解为因子对样本整体的贡献),此碎石图显示特征值在第六个主分量之后开始形成直线,因此,剩余的主分量在变异性中所占比率非常小(接近于零),并且可能不重要。所以选择特征值大于1的6个因子(FAC1_1、FAC1_2、FAC1_3、FAC1_4、FAC1_5、FAC1_6)作为公共因子,也就是说剩下的因子都能由这6个来涵盖。其因子数与因子特征值如图2所示。 图2 因子数与因子特征值 3.2.3 计算综合得分及排名 以各公因子所对应的方差贡献率比例作为权重计算综合得分及排名。 综合得分Q=FAC1_1×33.041/83.12+FAC2_1×23.794/83.12+FAC3_1×9.445/83.12+FAC4_1×6.57/83.12+FAC5_1×5.61/83.12+FAC6_1×4.665/83.12。 对得出的综合主成分值,根据实际结果、经验与原始数据进行了检验,符合实际情况。根据综合得分公式计算营业厅得分及排名情况,营业厅综合得分及排名后20名见表2,营业厅综合得分及排名前10名见表3。 表2 营业厅综合得分及排名后20名 续表2 表3 营业厅综合得分及排名前10名 本文以主成分及因子分析方法为基础,通过构建营业厅分析评价模型,并将其运用于营业厅综合得分排名实证研究中。该模型从原始指标出发,寻找少数几个主成分[9]或共同因子作为新的评价指标,从而降低评价指标的维数,可以在信息量损失尽量少的情况下减少评价工作量。该方法具有客观性,评价数据来源于原始指标,不是人为确定,因此减少了人为判断因素造成评价结果的偏差。分析过程完成了去量纲、去相关性、降维、定权数等工作,最后建立1个营业厅综合评价模型,并计算出综合得分和排名。 通过分析营业厅综合得分及排名情况,业务部门可以结合实际情况,因地制宜地制定相关措施进行营业厅资源的合理配置[10],如条件成熟,可考虑撤并,在确保服务质量的前提下,实现营业厅工作提质增效。 本文充分利用电力营销业务系统营业厅线上指标数据,获取需要评价的各营业厅与工作量指标相关的17类指标数据,构建基于因子分析法的供电营业厅分析评价模型,计算营业厅得分及综合排名。通过分析评价结果,给出了排名较高及排名较低营业厅列表,为资源优化配置提供借鉴,能够在一定程度上反映营业厅资源效率的配置情况。
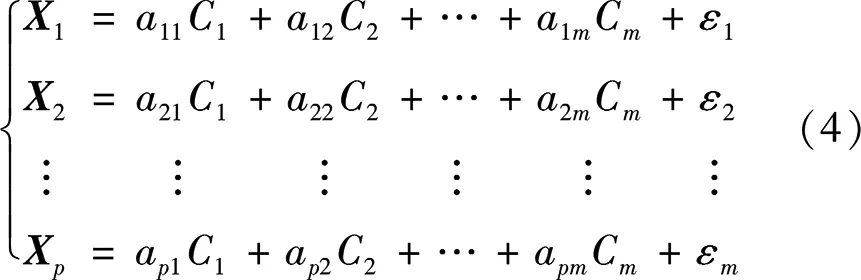
2 基于因子分析法的供电营业厅分析评价模型
2.1 建立营业厅指标体系
2.2 分析评价模型
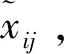
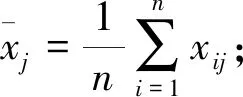
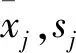
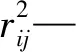
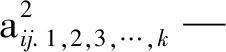
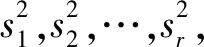
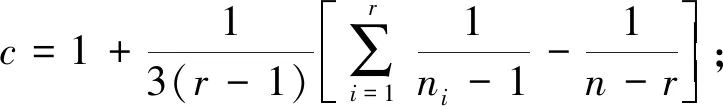
3 实例分析
3.1 数据处理
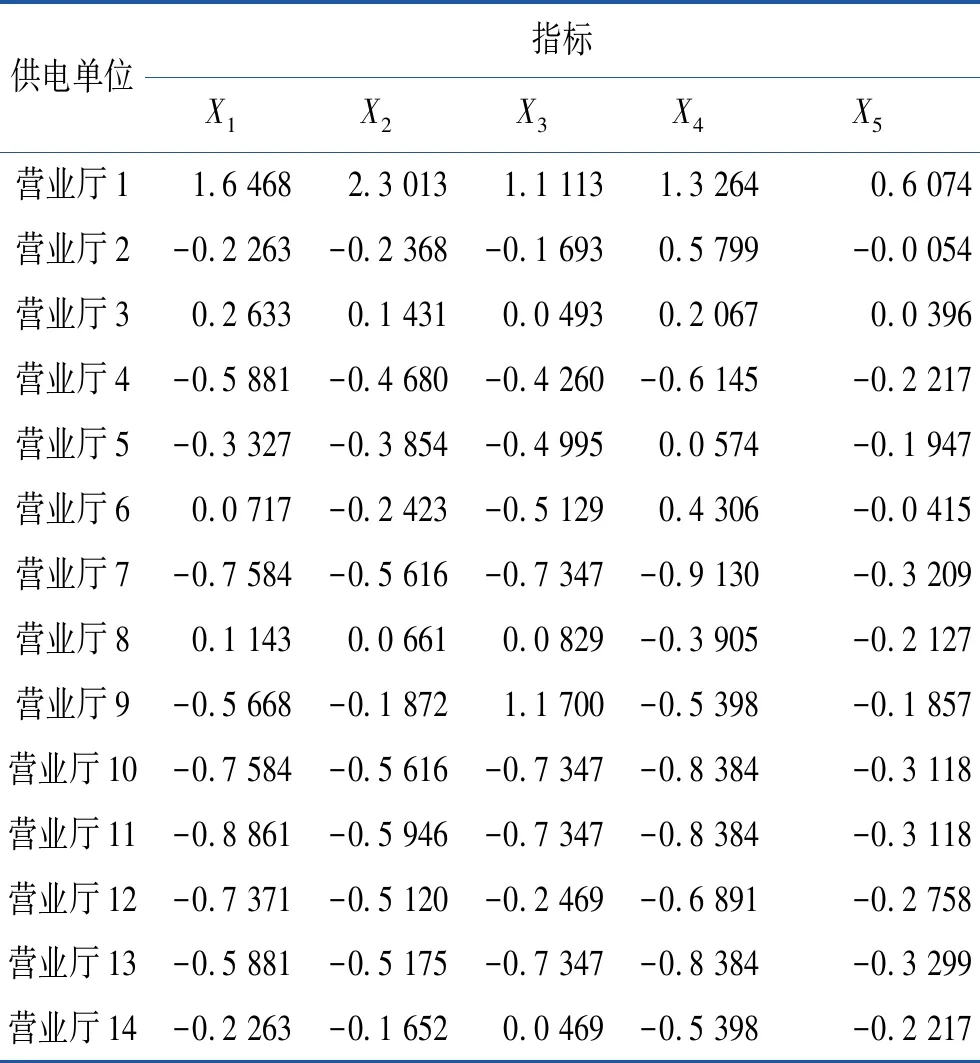
3.2 分析评价模型实现
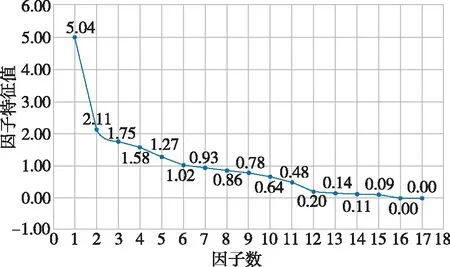
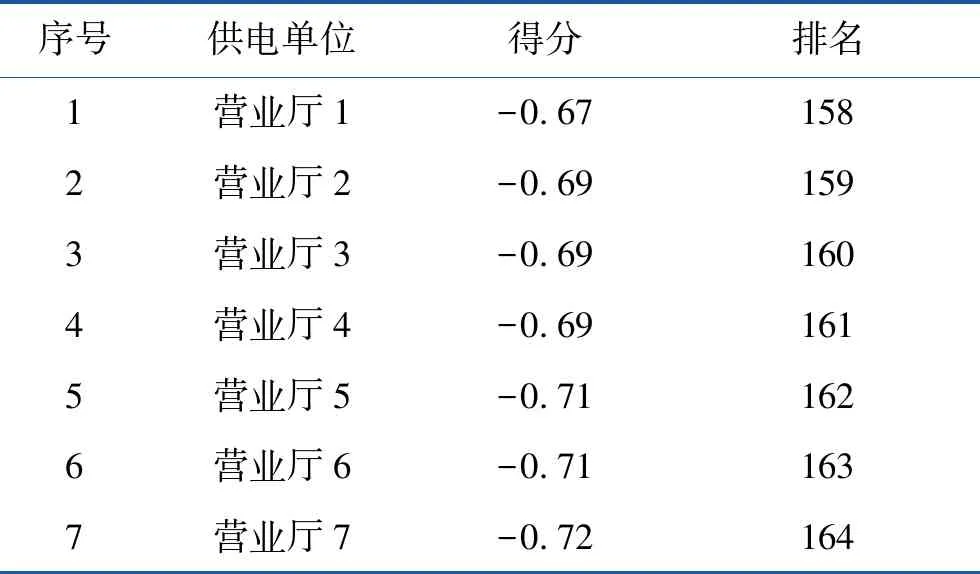
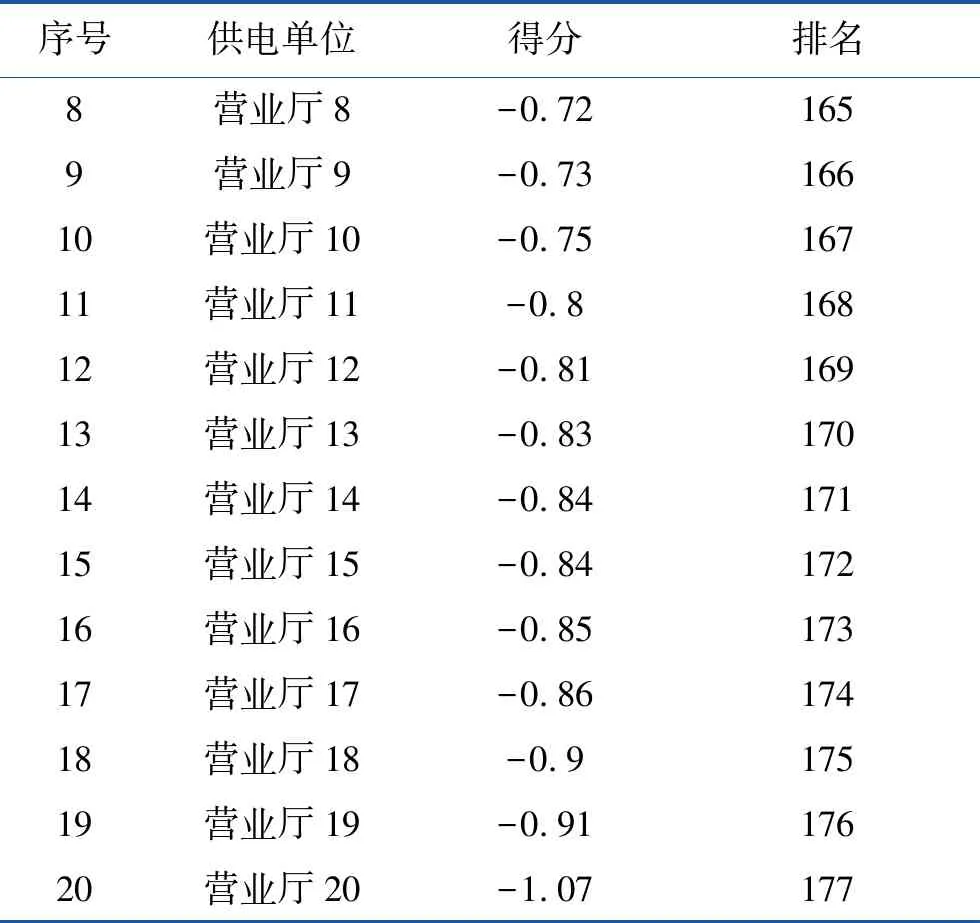
3.3 评价结果分析及建议
4 结 论

