转子过负荷保护中转化系数选取问题研究

朱建华，聂丽丽，关延伟，许立长，李雷，孙亮，余方令

(润电能源科学技术有限公司 电气技术中心，河南 郑州 450000)

0 引 言

励磁系统是发电机系统的重要组成部分，其正常运行对电力系统有着重要意义[1-3]。转子过负荷保护是保证发电机本体安全的重要保护之一，转子过负荷保护反映发电机强励工况下的允许运行时间，目前转子过负荷保护多采用励磁变电流作为保护的判定量，且研究多是针对转子过负荷保护与过励限制的配合[4-8]，整定转子过负荷保护定值时需将励磁直流电流等效为交流侧电流，目前转子过负荷保护定值整定计算中多采用触发角等于0°时的交直流电流转化系数，该值一般为0.816，但发电机励磁系统在强励时触发角一般大于0°，变化范围在10°～20°之间，故目前交直流电流的转化系数未考虑强励工况对交直流侧电流转化关系的影响。

目前转子过负荷保护整定研究中，文献[9]给出励磁变的交直流电流转化比值为0.816，且继电保护整定规程中也采用该数值。文献[10-11]给出了励磁整流器交流侧全波电流和直流侧电流之间的函数关系，该函数与触发角和换相角密切相关。文献[12-14]给出励磁整流器交流侧基波电流有效值和直流侧电流有效值之间的函数表达式，且该表达式是触发角和换相角的函数。目前的励磁交直流转化关系在触发角为0°时计算得出，实际励磁系统为了保证系统稳定性和设备安全，触发角一般大于10°，所以0.816的系数并没有反映强励工况下触发角的变化趋势，也没有准确反映各种工况下的交流侧基波电流和直流电流之间的转换关系。

本文通过理论分析和仿真计算结合的方法验证交直流侧电流的转化系数，拟通过本文研究，使得该转化系数能够反映发电机励磁绕组在不同的运行工况下的变化情况，研究成果对转子过负荷保护的参数准确整定有着重要参考意义。

1 转化系数的推导

励磁系统的功率整流器多采用三相整流器，三相整流器的换相过程如图1所示。

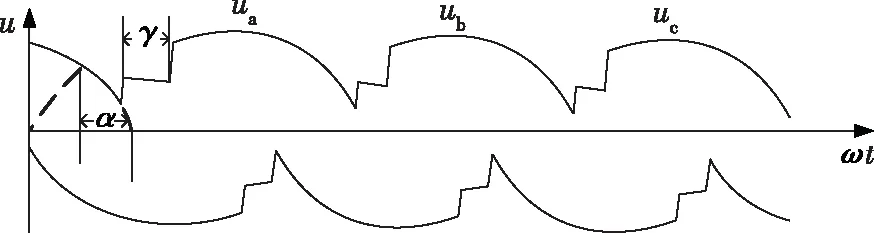
图1 三相变流器换相过程

图1描述的三相整流器的换相过程中主要变量：ωt为发电机角速度ω与时间t的乘积；α为触发角，具体指的是两相电压相等对应的时间点与下一次最近的电压等于零点时间差换算成的角度值；γ为换相角，表示待导通阀与将关闭阀的换流过程时间差值对应的角度值。

换相过程的等值电路如图2所示。

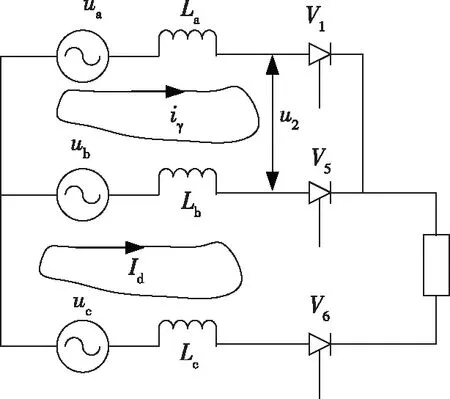
图2 换相过程的等值电路

图2中：ua，ub，uc为三相交流侧电源电压；La，Lb，Lc为三相电感；V1，V5，V6为阀组名称。图2所示的换相过程中，由于ua>uc，换相电流由a相流向c相。Id为整流桥的输出电流。

励磁整流器将励磁变的交流电流转化为直流电流时，交流侧电压U2需要经历换相过程，换相过程中电流方程[15]为

(1)

阀电流为整流桥的输出电流Id的表达式为

(2)

式中：Id—非换相期间的阀电流。

换相上升时段的电流公式为

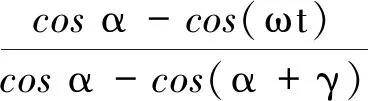
(3)

同样，换相过程下降时段的电流为

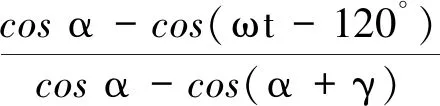
(4)

整个换相时段的阀电流IT(RMS)的表达式为

(5)

式中：ψ(α,γ)对应表达式为

(6)

需要特别说明的是，本文计算出的表达式与文献[10-11]并不相同。使用软件对比本文的值和文献[10-11]的值，发现根据文献[2-3]计算出的值在多数工况下均大于1/3。根据文献[11]中的公式(9)计算出的有效值转化系数为复数，违背电流表达式的计算规律，故本文采用形式如式(6)的表达式。

在同一个周期内，整流桥交流电流由两个同相阀的电流组成，故整流器交流侧电流的有效值与直流侧电流的关系为

(7)

同样的，交流侧电流的基波值I2b和直流侧电流的关系为

(8)

2 分析过程

2.1 转化系数对热容量系数的影响

采用不同的转化系数对发电机转子热容量系数的计算会产生一定影响，可以根据式(9)计算出对应的允许时间：

t=C/[(If/Ifbase)2-1]

(9)

式中：t—过励允许时间；

If—励磁直流电流；

Ifbase—励磁基准电流；

C—热容量系数。

热容量系数一般由励磁电流顶值对应的允许过励时间确定：

C=tmax[(Ifmax/Ifbase)2-1]

(10)

式中：tmax—最大励磁电流下的允许时间；

Ifmax—最大励磁直流电流；

Ifbase—励磁基准电流。

实际中转子过负荷保护整定计算中，转子过负荷保护一般采用励磁变交流电流代替励磁直流电流表示转子的过负荷特性，两者的转化关系为

C=tmax[(0.816Ifmax/Ifbase)2-1]

(11)

但实际中转子电流一般采集励磁变交流电流模拟量，再使用傅里叶变换计算出基波电流有效值，采用基波电流有效值计算出的热容量系数为

Cr=tmax[(0.78Ifmax/Ifbase)2-1]

(12)

式中：Cr—真实的热容量系数。

以常见的300 MW火电机组为例，一般允许最大过励电流为2.09倍额定励磁电流，允许过载时间为10 s，根据全波有效值计算出的0.816系数对应热容量系数为35.7，而根据基波有效值计算出的热容量系数为33.7。对比两者，根据全波有效值整定出的热容量系数可能超出发电机转子热容量极限，超出比例为6%左右，会对发电机的设备安全造成一定危害。

2.2 运行工况对转化系数的影响

发电机在不同运行工况下触发角和换相角会发生明显变化，特别在强励运行时转子过负荷保护可能会动作。为验证发电机转子过负荷保护动作的正确性，需要模拟发电机在不同工况下发电机的触发角和换相角的变化趋势，计算出交流量和直流量的转化系数。发电机在触发角保持恒定情况下，换相角不断变化，根据公式(7)计算出不同触发角和换相角情况下的转化系数，如图3所示。

从图3可以看出：触发角越小，对应的全波转化系数越小；发电机机端电压越低，对应的触发角越小。当机端短路时，对应的触发角最小，说明发电机在机端电压最低时，对应的全波转化系数最大，最小值约为0.8。

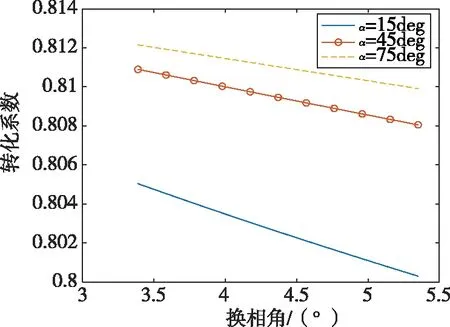
图3 不同工况下的全波转化系数

发电机在触发角保持恒定情况下，换相角不断变化，根据公式(8)计算出不同触发角和换相角情况下的转化系数，如图4所示。

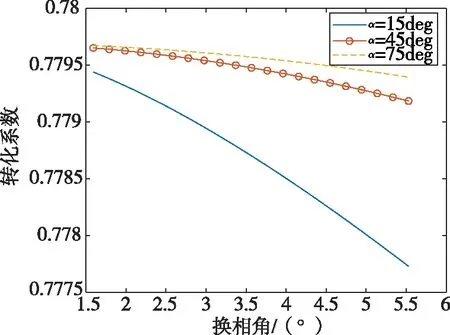
图4 不同工况下的基波转化系数

从图4可以看出：触发角越小，对应基波转化系数越小；换相角越大，对应的基波转化系数越小。基波转化系数变化规律与全波转化系数变化规律基本一致。且基波转化系数变化范围很小，最大值与最小值差异在0.25%左右。较小的差异性给转子过负荷保护整定基本上提供了便利，可以在参数整定时不考虑发电机工况的影响，选取恒定的转化系数，减轻了保护定值计算过程中的繁琐程度。

2.3 仿真模型

为验证转化系数计算的正确性，在仿真平台搭建6脉动整流器模型，输出励磁变的交流侧电流和励磁直流侧电流，比较两者的变化规律，对应波形如图5所示。

从图5可以看出，在整流器进入稳定状态后，即0.02 s后，直流侧电流和交流侧电流进入稳态，两者之间的比值恒定。直流侧电流有效值为318 A左右，交流侧电流有效值为124 A左右，计算出两者比值为0.779 9。与公式(8)计算出的转化系数基本一致，说明本文计算方法的有效性。

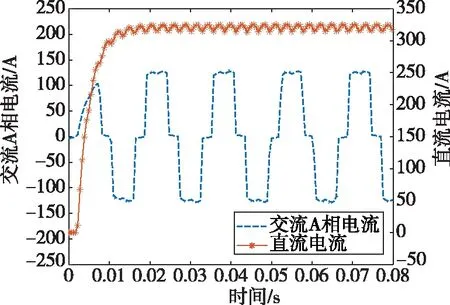
图5 交流电流和直流电流对比曲线

2.4 时域仿真

为进一步研究转化系数对转子过负荷保护动作的影响，在PSASP软件平台中搭建单机无穷大系统，发电机参数如下：

额定有功P=200 MW,额定机端电压UN=13.8 kV，d轴同步电抗Xd=1.305 p.u.,d轴暂态同步电抗Xd′=0.296 p.u.,d轴次暂态同步电抗Xd″=0.252 p.u.,q轴同步电抗Xq=0.474 p.u.,q轴暂态同步电抗Xq′=0.243 p.u.,q轴次暂态同步电抗Xq″=0.18 p.u.。基准功率为额定视在功率，基准电压为额定机端电压。

d轴暂态短路时间常数Td′=1.01 s,d轴次暂态短路时间常数Td″=0.053 s,q轴开路次同步时间常数Tq″=0.1 s。

惯性时间常数Tj=6.4 s。

升压变容量为210 MVA，变比为13.8 kV/220 kV，短路阻抗百分比为16%。

无穷大系数用10 000 MVA的发电机等值，发电机阶数为2阶，惯性时间常数设置为10 000 s，可以近似认为系统发电机转速恒定。

在发电机机端设置短路故障，故障开始时间为0.1 s，切除时间为0.5 s，采集发电机励磁电流，根据公式(9)原理计算出发电机的转子过负荷动作后累积的热容量系数，分别根据公式(12)将热容量系数等于35.7和33.7时转子过负荷保护启动时间记录下来，对应动作时间见图6。

从图6可以看出，在发电机机端发生短路时，采用基波算法时动作时间为12.7 s，采用全波算法动作时间为13.4 s，两者的误差在5.5%左右。说明不同的折算系数对转子过负荷保护动作时间产生一定的不利影响。

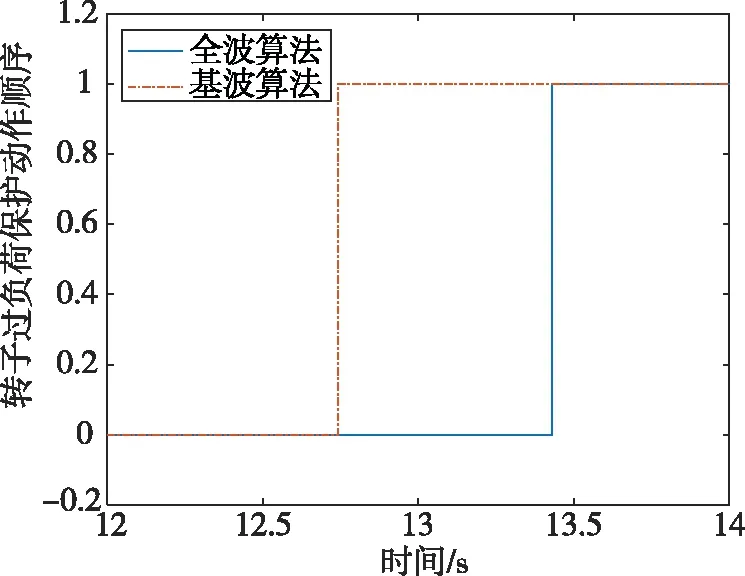
图6 机端短路时动作时间的差异

在高压侧机端设置短路故障，故障开始时间为0.1 s，切除时间为0.5 s，两种算法的动作时间差异如图7所示。

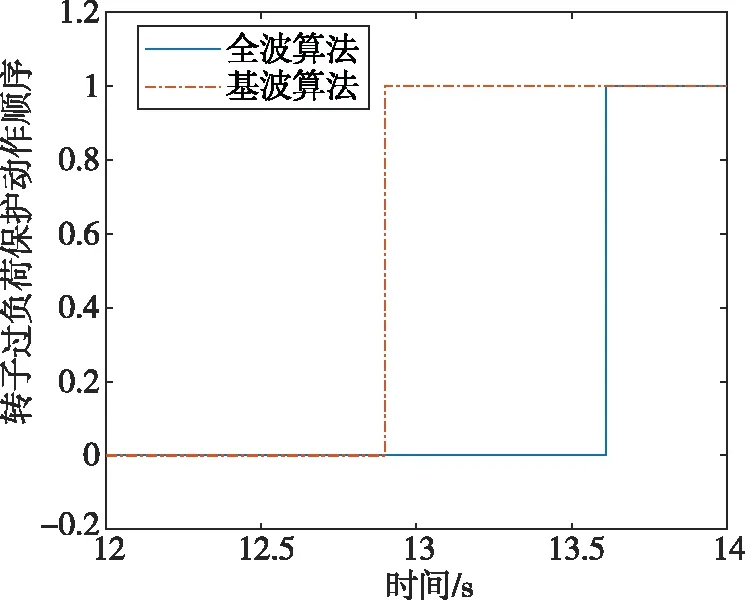
图7 机端短路时动作时间的差异

在机端电压短路时，两种算法的动作时间差异在0.7 s左右，基本上与机端短路时差异不大。

3 结 论

本文研究发电机转子过负荷保护中励磁交流电流和直流之间转化系数的选取问题，得出转化系数基本上保持恒定，受发电机工况变化影响很小的结论，且实际保护测量时多采用基波分量的有效值，建议用0.78系数代替目前普遍采用的0.816系数。该结论为发电机转子过负荷保护参数整定和采集励磁变交流电流用于监测励磁直流电流时的参数设置提供重要技术参考。