基于向量自回归和多元线性回归的区间序列预测方法

乌 兰, 曾祥艳, 周 伟

(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

面向区间序列的预测模型在大数据时代具有很好的应用价值。很多研究者已经提出了一些区间序列的预测方法,其中一类方法是将区间序列拆分成中点、半径、面积、灰度等精确数序列,再建立自回归移动平均模型(ARMA)、灰色模型(GM)等[1-3]。这类方法考虑了区间的整体性,预测效果主要依赖区间中点序列,但是并未使预测模型直接适用于区间序列。另一类方法是改进预测模型的参数设置,使模型能直接对区间建模。例如,将灰色模型的发展系数取为区间上下界点序列发展系数的加权平均值,使模型能直接对区间序列建模,但是这种加权平均方法弱化了区间上下界点序列各自的发展趋势,对振荡型区间序列预测效果较差[4-5]。

2011年,Maria等[6]提出了区间Holt 指数平滑方法(Holt)来预测区间序列。该方法将区间看作一个二维列向量,将Holt指数平滑模型的平滑系数由实数改为矩阵,再直接对区间进行平滑处理,考虑了区间上下界点的内在联系。文献[7]进一步将该方法与多输出支持向量回归(MSVR)结合,也取得了很好的效果。该方法也被引入灰色模型,构成一系列矩阵型灰色模型,对区间序列预测效果良好[8-10]。该方法类似于向量自回归模型(VAR)的建模机理,即考虑构成向量的几个内生变量之间的相互联系,所以VAR常用于预测相互联系的几个变量,是处理多个相关工程或经济指标的分析与预测的主流模型之一[11-13]。鉴于此,将区间看作列向量,用VAR 和向量多元线性回归模型(VMLR)进行预测考虑区间的上下界点之间的相互联系。

1 面向区间序列的向量回归组合模型

VAR是考虑了构成向量的几个内生变量之间的相互联系而建模的。多维移动平均(MA)和ARMA模型也是转换成VAR模型,所以近年来VAR模型受到越来越多的经济工作者的重视。

定义1 具有以下结构的模型称为面向区间序列的向量自回归模型(IVAR):

VAR模型只考虑了因变量序列的滞后性和前后影响,未考虑外在的关联因素对因变量的影响。因此,将进一步建立面向区间序列的多元线性回归模型(MLR)。目前,MLR 只适用于精确数序列,这里类似于VAR模型,将其向量化。

定义2 具有以下结构的模型称为面向区间序列的向量多元线性回归模型(IVMLR):

以下同时考虑被预测变量的内在和外在因素,给出面向区间序列的向量自回归和向量多元线性回归组合模型。

定义3 具有以下结构的模型称为面向区间序列的向量自回归和向量多元线性回归组合模型,简称为向量回归组合模型(IVAR-MLR):

2 模型定阶

建立IVAR模型需要解决以下2个主要问题:

1) 区间的下上界点这2个内生变量之间是否具有相关关系,要用“格兰杰因果性”检验确定。但是,只有平稳序列才能做格兰杰检验。所以,首先要做“单位根检验”,即平稳性检验,本研究采用ADF(augmented Dickey-Fuller test)检验序列的平稳性。若非平稳,进行数据预处理,如取对数、差分。

2)IVAR模型的最大滞后阶数p的确定。若p过小,则误差项可能存在自相关,会导致参数估计的非一致性;加大p值,可以消除～ε(t)中存在的自相关。但是p值过大,待估参数太多,自由度降低,影响参数估计的有效性。常用的p值确定方法是赤池信息量准则(AIC)和施瓦茨(SC)准则。在增加p值的过程中,当IVAR模型的AIC和SC同时达到最小即可。对年度和季度数据,p值一般增加到4;对月度数据,p值一般增加到12。当AIC和SC的最小值对应不同的p值时,就用似然比(LR)检验法。

IVAR-MLR模型的最大滞后阶数p的确定方法与IVAR模型的确定方法相同。

3 模型的参数估计过程

以IVAR 模型为例,根据矩阵的运算法则可以将式(1)进行分解,得到2个线性方程:

由式(4)估计预测区间上界点yU(t)的参数,令

4 模型的预测公式

IVAR模型的区间上下界点的预测公式即为式(4)和式(5)。IVMLR 模型的区间上下界点的预测公式由式(2)分解可得:

由预测公式可看出,IVAR模型、IVMLR模型或IVAR-MLR模型中因变量的区间上界点不仅受自变量上界点的影响,同时还受自变量下界点的影响。同理,因变量的下界点也同时受自变量上下界点的影响。因此,因变量的各个界点不仅与自变量对应的界点有关,而且受自变量上下界点的整体影响,使得模型的适应性和协调性更强。因此,IVAR将区间的2个界点序列联合起来对其中一个界点进行预测,体现了区间的上下界点的整体性和相互影响关系。

5 实证分析

5.1 发电量预测

国家统计局提供了2010年至2019年全国年主营收入2 000万元及以上的工业企业的发电量数据,其中部分月份的数据缺失,缺失部分由2个月份的累计值相减得到。 将火力发电量和水力发电量作为发电量的相关因子。将一年4个季度按季度分成4期,将每个季度中发电量的最大值作为区间的上界,最小值作为区间的下界。部分建模数据见表1。

表1 原始区间TW·h

采用2010 年到2018 年的区间序列建模,对2019年4个季度的区间观察值进行预测效果检验。对于二维列向量形式的区间序列,可以将检验区间序列是否平稳转化为检验上下界序列是否平稳。从表1可看出,2010年到2018年的发电量区间序列的上下界的平稳性检验结果都为非平稳序列,因此将上下界点序列进行一阶差分,重新进行单位根检验,结果表明,经过一阶差分后,区间上下界点序列皆为平稳序列。对一阶差分序列采用VAR 模型最优滞后阶数定阶法进行确定。不同阶数的LR、AIC、SC值如表2所示。从表2可看出,在显著水平0.05的条件下,综合LR、AIC和SC值,将模型阶数定为3阶较为合适。

表2 滞后阶数选择结果

参数估计后IVAR模型的具体形式为IVAR-MLR模型的具体形式为

将2010—2018年的数据采用最小二乘法得到的IVAR-MLR模型参数估计,如表3所示。3个模型对2019年4个季度的预测结果见表4。

表3 IVAR-MLR模型参数估计结果

表4 发电量区间预测值TW·h

将区间均方误差(MSEI)、区间平均绝对误差(MAEI)、区间平均绝对百分比误差(MAPEI)作为衡量模型预测结果精确度的指标。具体表达形式为:

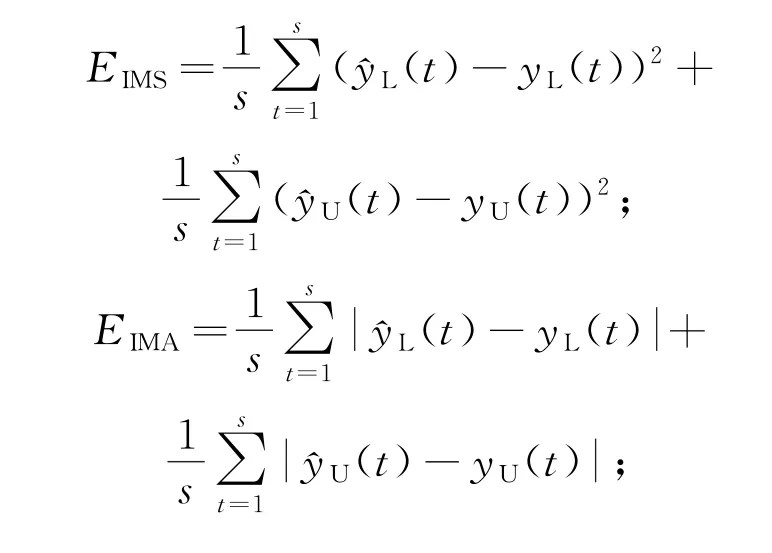
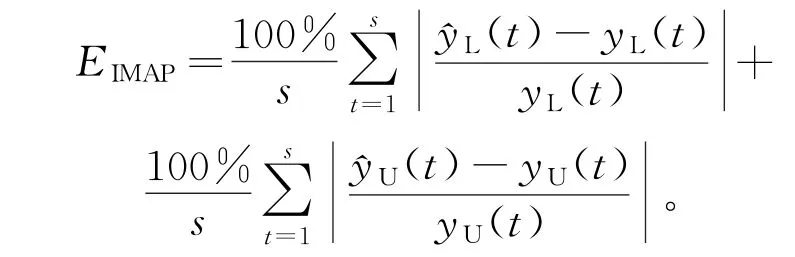
模型预测误差的具体结果见表5。

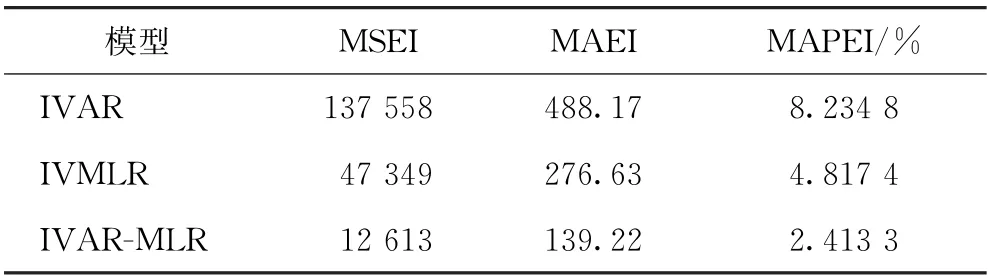
表5 预测误差分析

由表5可看出,IVAR-MLR 模型较其他2种模型的3 个指标更优,平均绝对百分比误差只有2.413 3%,精度较高。

5.2 客运量预测

国家统计局提供了2010—2019年全国客运量的数据～y(t),其中部分月份的客运量数据缺失,缺失部分由2个月份的累计值相减得到。将铁路客运量～x1(t)和公路客运量～x2(t)作为客运量的相关因子。将一年4个季度按季度分成4期,将每个季度中客运量的最大值作为区间的上界,最小值作为区间的下界。部分建模数据见表6。

表6 原始区间序列万

从表6可看出,从2010—2018年客运量区间序列的上下界的一阶差分序列为平稳序列。采用VAR模型最优滞后阶数定阶法,不同阶数的LR、AIC、SC值见表7。

表7 滞后阶数选择结果

由表7可知,在显著水平为0.05的条件下,综合LR、AIC和SC值,确定将模型阶数定为3阶较为合适。IVAR、IVMLR和IVAR-MLR模型的预测结果见表8,预测误差比较见表9。

表8 客运量区间预测值万

从表9可看出,IVMLR 模型和IVAR-MLR 模型的预测效果较好,平均绝对百分比误差只有1%左右,预测精度较高。

表9 预测误差分析

6 结束语

自回归模型考虑了时间序列的滞后性,多元线性回归模型考虑了时间序列的影响因素。本研究将区间看作列向量,将自回归、多元线性回归以及组合模型的参数设置为矩阵,使模型能直接对区间序列建模预测,拓广了他们的适用范围。分析结果表明,这种建模方法实质上是将区间的上下界点序列联合起来对其中一个界点序列进行预测,考虑了区间的整体性和上下界点的内在联系。在对发电量和客运量的预测中,组合模型预测效果稳定,表明了该区间预测方法的有效性。