一种求解稀疏逻辑回归问题的不精确邻近拟牛顿算法

杨 娅, 肖 斌, 胡清洁

(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.郑州商学院 通识教育中心,郑州 451200)

逻辑回归是一种针对二分类问题提出来的特殊的非线性回归模型,主要用于解决分类问题,在医学监测、文本分类等领域具有广泛应用。其中稀疏逻辑回归,也被称为l1正则化逻辑回归,是具有稀疏约束的经典逻辑回归模型,在神经网络[1-2]、深度学习[3]和生物信息学[4]等领域有着广泛的应用。

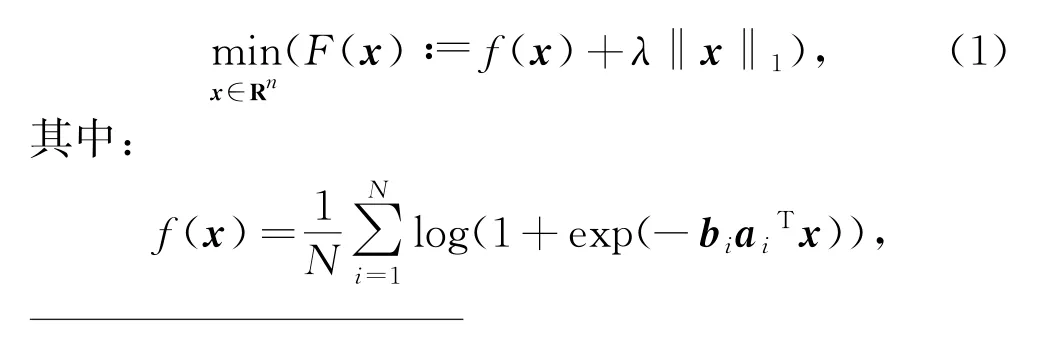
稀疏逻辑回归问题的数学模型表示为为平均逻辑损失函数;λ‖x‖1为l1正则化函数,λ>0。这个问题的输入数据是1个训练数据点集(a i,b i)∈Rn×{-1,1},i=1,2,…,N,N>0。由于问题(1)中的l1正则项可以产生稀疏解,从而在高维数据处理中占有显著优势,因此成为近些年来研究的热点。目前求解稀疏逻辑回归问题的算法有很多,例如快速迭代收缩阈值算法[5]、快速自适应收缩阈值算法[6]、交替方向乘子法[7]、邻近梯度算法[8]、邻近拟牛顿算法[8]等。

在利用邻近拟牛顿法求解问题(1)时,需要计算邻近算子[8],但在很多实际问题中,邻近算子问题无明显的解析解,或者有解析解但精确求解时计算量很大,所以很多情况下需考虑近似求解邻近算子。因此,针对问题(1),提出了求解该问题的不精确加速邻近拟牛顿算法,并给出相关收敛速度分析和数值实验。

1 不精确加速邻近拟牛顿算法

首先给出F(x)在点y的复合二次近似:

为在第k次迭代时计算出的不精确邻近算子的值。

基于Scheinberg等[8]提出的加速邻近拟牛顿算法,给出如下不精确加速邻近拟牛顿算法。

算法1 不精确加速邻近拟牛顿算法

8)k=k+1,转步骤2)。

该算法是文献[8]中算法5的一个不精确形式,在步骤3)计算邻近算子时引入不精确项εk。

2 算法的有关性质

为了分析不精确邻近拟牛顿算法的收敛速度,给出该算法的4个引理。首先给如下假设。

假设1:

1)f:Rn→R是光滑凸函数且梯度Lipschitz连续,其Lipschitz常数为L。

2)问题(1)是可解的,即存在x*∈Rn是F的最小值点。

3)对算法中矩阵序列{H k},假设存在正数m、M,对任意的k>0,有

该引理类似于文献[13]中的Remark27。

引理2[13]若f满足假设1,ε≥0,且

将式(2)与式(3)相加,可得

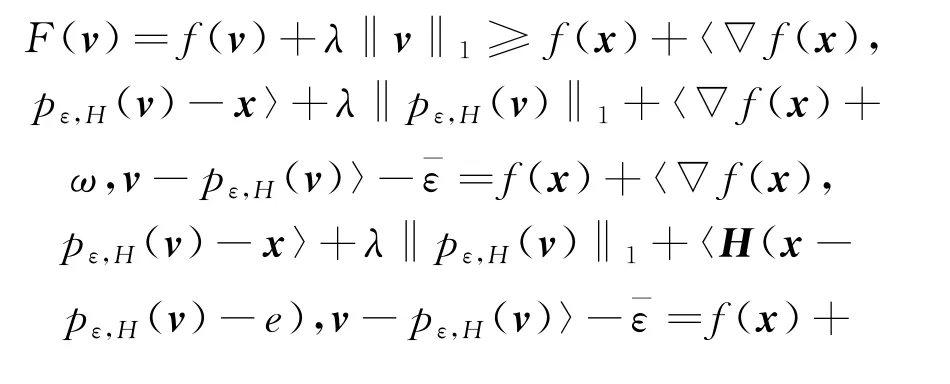
则下列不等式成立:

该引理来源于文献[13]中的引理3.3。

3 算法的收敛性分析

为了证明不精确加速邻近拟牛顿算法的收敛速度,给出如下假设:

假设2 给定a≥2,假设

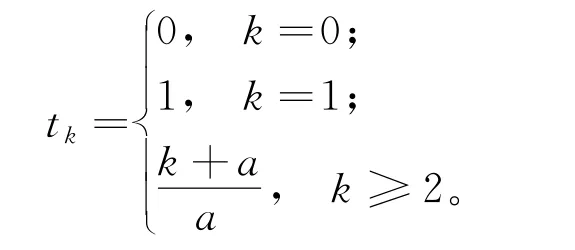
以下给出不精确加速邻近拟牛顿算法的收敛速度结果。

定理1 (收敛性)若假设1、假设2、假设3都成立,且σ0≤σk+1,定义

又由

故定理1得证。

4 数值实验

为了检验算法的有效性,将不精确加速邻近拟牛顿算法(NEWAPQNA)的数值结果与精确加速邻近拟牛顿算法(APQNA)[8]、不精确邻近拟牛顿算法(NEWPQNA)[8]、精确邻近拟牛顿算法(PQNA)[8]的数值结果进行比较。实验在MATLAB R2014b中运行,测试环境为Window 7 操作系统,intel(R)Core(TM)i5-6500 CPU@3.20 GHz,8.0 GiB RAM。

在NEWAPQN 和NEWPQNA 中利用随机坐标下降算法[8]求解不精确的邻近算子。经过调试,将最高迭代次数设为200次,将算法的终止条件设为10-8。

令ℓ=0.05,β=0.05,4种算法运行结果如图1、图2和表1所示。

表1 算法比较结果

图1 4种算法目标函数值相对误差变化

图2 4种算法迭代序列相对误差变化图

从图1、表1可看出,利用这4种算法求解稀疏逻辑回归问题所得的目标函数相对误差相近,但利用NEWPQNA 求解目标函数所需的迭代次数最少,效果更好。从图2可看出,APQNA、NEWPQNA、PQNA求解稀疏逻辑回归问题所得的绝对误差相近,但利用NEWPQNA相对误差稍优于其它3种算法,这表明不精确邻近拟牛顿算法效果更好。

5 结束语

为了更有效的求解稀疏逻辑回归问题,通过利用不精确算子,提出了一种不精确邻近拟牛顿算法,并证明了该算法的收敛速度。该算法改进了文献[8]中的加速邻近拟牛顿算法。数值试验结果表明,该算法对求解稀疏逻辑回归问题是有效的。