考虑孤岛源-荷不确定性的直流配电网可靠性评估

马 钰 韦 钢 李 扬 李 牧 邓申玮

（1. 上海电力大学电气工程学院 上海 200090 2. 国网浙江慈溪市供电有限公司 宁波 315300 3. 国网浙江省电力有限公司嘉兴供电公司 嘉兴 314000）

0 引言

直流配电网凭借其供电容量大、线路损耗小、更适于分布式电源（Distributed Generation, DG）接入等优势成为城市配电网研究的新方向[1-2]。为了适应DG 的接入，IEEE1547—2003 鼓励DG 以孤岛运行的方式向故障后停电的负荷供电，从而提高系统的可靠性及DG 的利用效率[3]。由于孤岛内DG 出力及负荷需求的波动性，孤岛形成具有较大的不确定性。因此研究考虑孤岛源-荷不确定性的直流配电网可靠性评估方法对直流配电系统的发展有着重要的实际意义。

目前国内外对于直流配电网的可靠性研究多集中于直流设备的可靠性建模，所采用的方法或模型主要有部件计数法、可靠性框图法、马尔科夫模型等。其中，部件计数法和可靠性框图法均仅根据设备的拓扑结构及元件数量建立设备的可靠性模型，未考虑设备的实际运行状态且忽略了元件的可修复性，适用于设备设计研究的早期[4-5]。随着直流设备逐渐投入工程运行，近年来马尔科夫模型在评估设备可靠性方面展现了其独特的优势。马尔科夫模型常用于描述系统的状态转移过程，文献[6]针对直流断路器建立了马尔科夫可靠性模型，证明了马尔科夫模型的有效性，但所建模型未考虑元件的运行状态且忽略了元件的冗余设置对设备可靠性的影响。

含DG 的配电网可靠性指标计算方法可分为解析法[7]和模拟法[8]两大类。解析法包括最小割集法、最小路法等；模拟法主要指蒙特卡洛法。文献[5]采用序贯蒙特卡洛法计算直流配电网的可靠性指标，有效地模拟了DG 的随机性，但并未考虑DG 自身故障及孤岛运行对直流配电网可靠性的影响。文献[9]利用最小割集法计算含DG 的直流配电网可靠性指标，考虑了孤岛运行方式对配电网可靠性的影响，但未考虑DG 及负荷的不确定性。文献[10]利用点估计法将孤岛运行期间内DG 出力及负荷需求按估计点组取为确定值，将对随机变量的概率可靠性计算转换为对多个估计点组的可靠性计算，在模拟DG 及负荷的不确定性方面不够准确。文献[11]提出计及DG 和负荷相关性的配电网可靠性评估方法，考虑了各随机变量间的相关性问题。文献[12]将DG等效为多容量状态的发电机，利用短期分析法计算孤岛形成概率，通过改进最小路法计算可靠性指标，但未结合DG 孤岛供电情况对最小路法进行改进。以上文献都考虑了DG 对配电网可靠性的影响，但仍然存在以下两点不足：①没有综合考虑孤岛内源-荷的不确定性和随机变量间的相关性对孤岛形成概率的影响；②由于孤岛内源-荷具有很强的不确定性，无法时刻满足供需平衡，孤岛内的负荷存在二次停电的风险[13]，因此需要考虑孤岛持续时间对系统可靠性的影响，但大多数研究未考虑这一因素。

针对以上问题，本文首先建立各直流设备计及运行状态和元件冗余度的马尔科夫可靠性模型；然后利用多场景技术模拟 DG 出力及负荷需求的特性，并在考虑孤岛持续时间的基础上计算孤岛形成概率；最后采用改进后的最小路法对直流配电网可靠性指标进行计算。

1 基于马尔科夫的直流设备可靠性建模

直流配电网能否安全可靠地运行与以电力电子器件为核心的换流器、直流变压器、直流断路器等关键设备的正常运行有直接的关系。本文采用马尔科夫模型对直流设备进行可靠性建模。

1.1 基于马尔科夫的直流设备可靠性模型

马尔科夫过程是一种随机过程，用以描述可修复系统中的状态转移过程。直流配电网中的直流设备是典型的可修复系统，设备中的元件可以在正常工作与故障两个状态之间切换，因此可以由马尔科夫状态过程描述。

1）马尔科夫过程

假设{X(t),t≥ 0}是取值在Q={0,1, …,n}上的一个随机过程，若对n个任意时刻点0＜t1＜… ＜tn，都有式（1）成立，则称{X(t),t≥ 0}为离散状态空间Q上的连续时间的马尔科夫过程。

2）基于马尔科夫过程做出的假设：①状态之间的转移是随机的，转移概率为常数；②同时出现两次及两次以上故障的概率为零；③系统和部件的状态均为互斥且离散的；④随机事件发生的时间服从指数分布。

1.2 换流器可靠性模型

模块化多电平换流器（Modular Multilevel Converter, MMC）的拓扑结构如图1 所示。MMC 由A、B、C 三相构成，每相分为上、下两个桥臂，桥臂由多个子模块（Sub-Modules，SM）与电抗器级联组成。SM 的拓扑结构有半桥型、全桥型、混合型三种，其中半桥型子模块由于可靠且经济而被广泛使用，因此本文选用半桥子模块对其进行可靠性分析。

图1 MMC 拓扑结构Fig.1 Topological structure of MMC

MMC 结构中的半桥子模块可以看作是由IGBT模块及电容器构成的串联系统，即只要有一个元件发生故障，系统就无法正常运行。其中，每个IGBT模块由一个绝缘栅双极型晶体管（IGBT）和一个反并联二极管构成。半桥子模块的故障率SMλ为

式中，λIGBT、Dλ和Cλ分别为IGBT、二极管、电容器的故障率。

MMC 中六个桥臂的拓扑结构完全相同，单个桥臂的可靠性在一定程度上可以表征MMC 的可靠性。为了有效提高MMC 的可靠性，桥臂上通常串联冗余的SM，使各模块互为冗余[14]。对于N+1 电平的MMC，其桥臂上通常串联N+M个SM，其中N为单个桥臂上为了保证换流器正常运行所必需的SM 数量，M为冗余SM 的数量。

换流器正常运行时，N个SM 全部投入运行，M个冗余SM 被旁路。当有一个SM 发生故障后，故障的SM 被旁路，冗余SM 从旁路状态切换为运行状态。故障的SM 可以通过维修或者更换，成为新的冗余SM。当故障SM 数量超过冗余SM 数量时，桥臂无法正常运行[15]。基于此，对于MMC 的单个桥臂进行马尔科夫可靠性建模，状态转移过程如图2 所示。

图2 MMC 单个桥臂的马尔科夫状态转移过程Fig.2 Markov state transition diagram of the single bridge arm of MMC

图2 中状态0 表示系统正常运行，状态 1,2, …,M表示系统中存在SM 故障，但系统仍能正常运行，状态M+1 表示系统故障。图2 中的SMλ、SMμ分别为SM 的故障率、修复率。根据状态转移图可得M+2阶系统状态转移密度矩阵为

列出系统的 Chapman-Kolmogorov 方程并设初始时刻系统处于正常运行状态，可得到微分方程组为

解式（5）可得系统的状态概率矩阵p(t)[16]。系统的可靠度函数R(t) 为所有非故障状态的概率函数之和，计算公式为

系统的平均无故障工作时间MTTF 和故障率λ计算公式为

1.3 直流变压器和直流断路器的可靠性模型

利用马尔科夫模型分别建立基于双有源全桥的输入串联输出并联（Double Active Bridge Input Series Output Parallel, DAB-ISOP）型直流变压器和混合式直流断路器的可靠性模型，具体过程与换流器的马尔科夫可靠性建模类似，由于篇幅限制，这里不再赘述。DAB-ISOP 型直流变压器和混合式直流断路器的拓扑结构图及对其建立的马尔科夫可靠性模型详见附录。

2 基于多场景技术的孤岛形成概率

DG 出力受环境因素影响较大且不可控，系统发生故障后DG 一般与储能设备相配合向孤岛内的负荷供电，从而改善系统的可靠性。本文采用多场景技术处理源-荷不确定性因素（包括DG 出力和负荷），在建立源-荷不确定性因素随机模型的基础上，通过拉丁超立方抽样（Latin Hypercube Sampling,LHS）、结合Nataf 变换的Cholesky 分解和同步回代场景缩减法（Synchronous Back Reduction, SBR）生成典型场景，计算典型场景下考虑孤岛持续时间的孤岛形成概率，以定量分析DG 接入对系统可靠性的影响。

2.1 不确定性因素的处理

2.1.1 风机出力随机模型

风机的出力PW(v) 与风速v有关，风速v可用Weibull 分布描述。当风速v位于切入风速vci和额定风速vrate之间时，风机出力的功率曲线可用线性函数表示[17]，则风机出力的概率密度函数为

2.1.3 负荷随机模型

采用正态分布描述负荷的不确定性，建立负荷的随机模型。i节点有功负荷为PL,i～N(μP,i,σP,i)，无功负荷为QL,i～N(μQ,i,σQ,i)，其中μP,i、μQ,i、σP,i和σQ,i分别为PL,i和QL,i的均值和方差。

2.1.4 多场景技术对不确定性因素的处理

1）LHS 技术生成场景

LHS 技术属于分层抽样，可以较好地解决蒙特卡洛法等随机抽样方法可能出现的抽样样本聚集的问题，保证样本可以全面覆盖变量的随机分布区域[18]。其核心思想是：将随机变量的分布取值空间[0,1]分成n个等间距不重叠的区间，再随机从各个区间内抽取一个值代表该区间的值，通过随机变量分布函数对应的反函数计算各区间的采样值。本文以1h 为单位时段进行分析，即t=1,2, … ,T，取T=24，对m个随机变量按时序依次进行抽样，可以得到24m×n阶样本矩阵R，R即为初始样本场景集。

2）结合Nataf 变换的Cholesky 分解

为获得随机变量相关性符合实际的样本，同时解决Cholesky 分解仅适用于服从正态分布的随机变量的问题[19]，采用结合Nataf 变换的Cholesky 分解，对不服从正态分布的随机变量的样本空间正态化处理并对样本进行重新排列，使样本值相关性接近随机变量之间的相关性。其主要步骤如下：

（1）随机生成24m×n阶顺序矩阵L，其中每一行元素由整数1,2, …,n随机排列而成，计算L的秩相关系数Lρ。

式中，新生成的顺序矩阵G中的元素不再是整数；D为下三角矩阵。

（4）令随机变量的秩相关系数矩阵为ρX，按式（12）对ρX进行Cholesky 分解，分别得到下三角矩阵Q和矩阵G*。

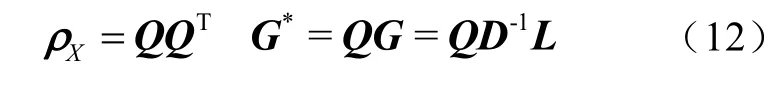
（5）根据*G中元素排列顺序对L中每行元素进行重新排列，生成的顺序矩阵记为*L。

（6）对初始矩阵R中每行元素按照*L中对应行元素的排列顺序重新排列，生成接近随机变量相关性的样本矩阵。

3）场景削减

LHS 技术生成的样本矩阵*R的场景数过于庞大，为提高计算效率，采用SBR 法对原始场景进行削减，筛选出能充分描述随机变量的典型场景集C（典型场景总数为C个），并计算出典型场景c出现的概率cπ，详细流程见文献[20]。

2.2 孤岛形成概率

为简化分析，文中以计划孤岛作为分析对象。根据DG 容量大小和负荷水平，以孤岛范围内的等值有效负荷最大为目标函数，在满足约束条件的基础上，采用广度优先搜索法[21]得到计划孤岛区域。

3 考虑孤岛形成概率的直流配电网可靠性评估

相较于模拟法，解析法具有模型准确、计算耗时少等优点。本文选用解析法中的最小路法[12]计算系统可靠性指标，在考虑DG 供电情况及孤岛形成概率的基础上对最小路法进行了改进，使其适用于含DG 的直流配电网的可靠性指标计算。

3.1 最小路、非最小路可靠性参数的计算与折算

首先通过Dijkstra 算法[23]得到所有负荷点至上级电源点的最小路集（负荷点i的最小路集为Si），再判断负荷点、馈线是否在孤岛内，分以下两种情况对负荷点的最小路、非最小路可靠性指标进行计算与折算。Case1：负荷点i在计划孤岛内，最小路或非最小路馈线不在计划孤岛内。Case2：负荷点i在计划孤岛内，最小路或非最小路馈线也在计划孤岛内；负荷点i在计划孤岛外。

3.1.1 最小路可靠性参数的计算

3.1.2 非最小路可靠性参数的折算

非最小路中的元件需要利用串联等效法将其可靠性参数折算到对应的最小路节点上。若非最小路馈线首端装有直流断路器和熔断器等能即时开断的设备，则该馈线故障对负荷点无影响。若非最小路馈线首端没有能即时开断的设备，则需判断能够隔离该馈线故障的开关是否在负荷点i的最小路上。

3.2 负荷点可靠性参数的计算

综上所述，孤岛外负荷点i的可靠性指标公式为

对于孤岛内负荷点i的可靠性指标计算，需考虑DG 供电情况对其进行修正，计算公式为

考虑孤岛运行方式对孤岛内负荷点可靠性指标的影响，对式（20）进行修正，利用全概率公式可得孤岛内负荷点i的可靠性指标公式为

3.3 可靠性评估流程

综上所述，考虑孤岛源-荷不确定性的直流配电网可靠性评估的计算流程如图3 所示，其中系统可靠性指标包括系统平均停电频率指标SAIFI、系统平均停电持续时间指标SAIDI、用户平均停电持续时间指标CAIDI 以及系统平均供电可用率指标ASAI。

图3 考虑源-荷不确定性的直流配电网可靠性评估流程Fig.3 Flow chart of reliability evaluation of DC distribution considering source-load uncertainty

4 算例分析

4.1 原始参数及测试系统

本文以改造后的IEEE-RBTS BUS6 主馈线F4系统[12]作为算例系统进行可靠性评估，其接线图如图4 所示。该系统采用双极直流供电，首端直流母线额定电压为±7.5kV，包含1 个换流器、23 台直流变压器、6 个直流断路器及23 个负荷点，负荷数据见附表1。每条负荷支路首端均配有隔离开关和熔断器。隔离开关操作时间γG=0.3h ，孤岛切换操作时间γF=0.2h，孤岛持续时间td=3h。在节点18、25处分别接入光伏机组和风电机组，风电机组、光伏机组参数如下：选取广西北海市涠洲岛全年8 760h的风速数据和光照强度数据进行拟合[24]，且PWN=1MW ，切入、切出和额定风速分别为3m/s、20m/s 和13m/s，PPVN=1MW 。储能设备容量上、下限为2MW · h和200kW · h，Pb,max=1MW 。

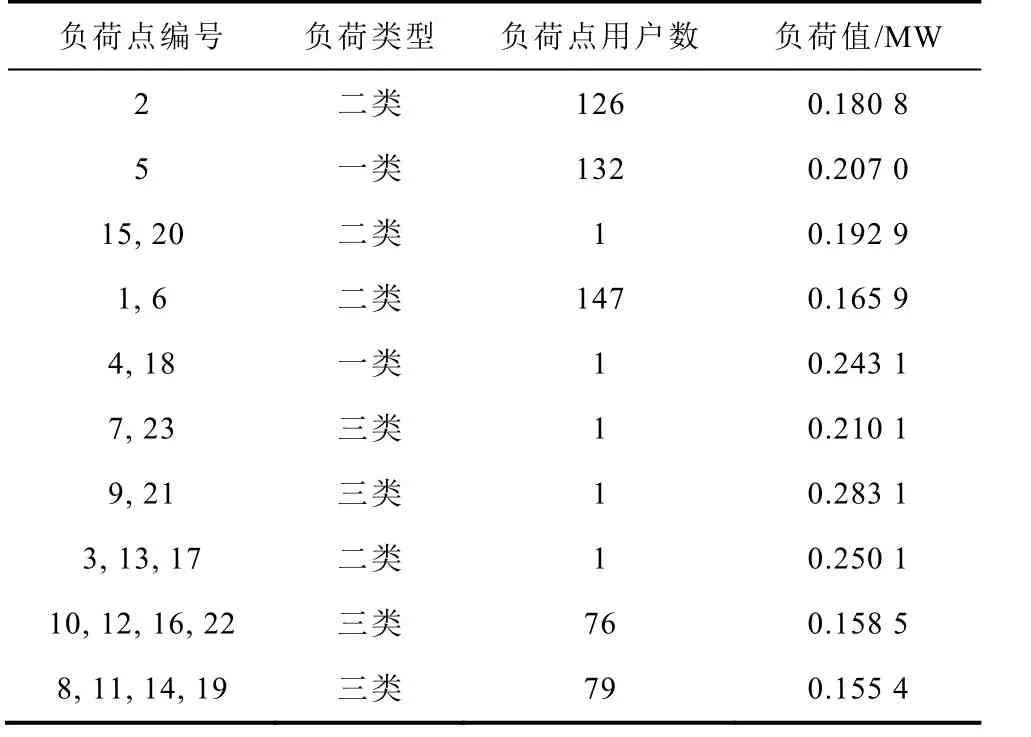
附表1 负荷数据App.Tab.1 Load data

图4 改进后的含DG 直流配电网可靠性测试系统Fig.4 Test system of DC distribution considering DG

4.2 可靠性指标计算与分析

4.2.1 直流设备可靠性指标计算

MMC 直流侧电压为 ±7.5kV，SM 中的IGBT 型号为1 700V/600A，各部件可靠性参数见附表2。根据直流侧额定电压和SM 额定电压计算单个桥臂上的SM 数量，考虑40%的冗余度，则单个桥臂需要七个SM，其中两个SM 为冗余SM。对MMC 的单个桥臂进行马尔科夫可靠性建模，可得单个桥臂的故障率为0.151 48，则MMC 的故障率为1.060 36。同理对直流变压器及直流断路器进行部件选型，并在考虑一定冗余度的情况下计算设备所需的元器件数量，分别建立直流变压器及直流断路器的马尔科夫可靠性模型，可得各个设备的可靠性参数，详见附表3、附表4。综上所述，直流配电网中关键元件可靠性参数计算结果见表1。

表1 直流配电网中关键元件可靠性指标Tab.1 Reliability indices of DC equipment

附表2 MMC 可靠性参数App.Tab.2 Reliability parameters of the MMC

附表3 直流变压器可靠性参数App.Tab.3 Reliability parameters of the DCSST

附表4 混合式直流断路器可靠性参数App.Tab.4 Reliability parameters of the hybrid DC circuit breaker

4.2.2 孤岛源-荷不确定性因素的模拟

采样规模n=500，典型场景数量设定为C=10 ，风速与光照强度、负荷的相关系数[25]分别为-0.2 和-0.25，光照强度与负荷的相关系数为0.4。利用2.1.4节的多场景技术得到随机变量典型场景如附图5～附图7 所示，各典型场景出现的概率如图5 所示。基于广度优先搜索法[21]对配电网进行最优孤岛划分得到的计划孤岛如图4 所示。计算不同场景下的孤岛形成概率结果见表2。

附图5 风机出力典型场景App.Fig.5 Typical scenarios of fan output

附图6 光伏出力典型场景App.Fig.6 Typical scenarios of PV output

附图7 负荷需求典型场景App.Fig.7 Typical scenarios of load demand

表2 各典型场景孤岛形成概率Tab.2 Probability of island formation in each typical scenario

图5 各典型场景出现的概率Fig.5 Probability of each typical scenario

为说明SBR 场景削减得到的10 个场景具有典型性，将其仿真结果与K-medoids 聚类方法[26]进行对比，比较两种方法的场景评价指标[26]，结果见表3。可以看到，本文SBR 方法生成场景的概率分布拟合方差和误差区间覆盖率指标均优于K-medoids 聚类方法，本文SBR 方法生成的场景更具典型性。

表3 场景评价指标对比Tab.3 Comparison of scenario evaluation indices

4.2.3 负荷点、系统可靠性指标计算

为了研究DG 不确定性和随机变量间相关性对直流配电网可靠性指标的影响，本文对以下四种情况进行计算分析：情况1——不含DG 的直流配电网；情况2——DG 接入，但不考虑孤岛期间DG 和负荷的不确定性（孤岛内供需始终平衡）及随机变量间相关性；情况3——DG 接入，考虑孤岛期间DG和负荷的不确定性，不考虑随机变量间相关性；情况4——DG 接入，考虑DG 和负荷的不确定性、随机变量间相关性。

用本文所提方法分别对上述四种情况部分负荷点及系统的可靠性指标进行计算，结果见表4、表5。同时为了验证本文综合考虑孤岛源-荷不确定性及孤岛持续时间影响下的孤岛形成概率的配电网可靠性评估方法的有效性，将本文方法与未考虑孤岛持续时间的计算方法[11]、DG 孤岛作用体现在对传统可靠性指标修正的方法[5]进行对比，结果见表5。

表4 不同情况下的部分负荷点可靠性指标Tab.4 Reliability indices of some load points of different cases

（续）

表5 不同情况下的系统可靠性指标Tab.5 Reliability indices of system of different cases

对比分析表4 中各种情况下负荷点可靠性指标可得：

1）DG 的接入对计划孤岛外的负荷的可靠性没有影响，计划孤岛内的负荷点故障率λ值有所上升，但是平均故障修复时间γ及年平均停电时间U指标都得到了一定程度的改善，这是因为计算孤岛内的负荷点故障率时需将DG 自身的故障率考虑进去，发生故障后孤岛成功形成可以减少负荷的停电时间。

2）对比情况2 和情况3 的数据可得，DG 的不确定性会影响孤岛内负荷点的可靠性指标，λ、γ和U值均略微上升。这是因为考虑DG 不确定性后，在td内孤岛内的供需并不是实时平衡的，孤岛具有很大的不确定性，负荷停电时间增加。

3）对比情况3 和情况4 的数据，考虑风速和光照强度、负荷负相关，光照强度和负荷正相关后，风机孤岛内负荷点15 的可靠性指标λ、γ和值均略微下降，光伏孤岛内负荷点23 的可靠性指标λ、γ和U值均略微上升。可以得出当风速（或光照强度）和负荷负相关时，DG 出力小于孤岛内负荷需求的概率减小，孤岛稳定运行的概率增大，负荷点可靠性增加；相反地，考虑正相关则可靠性指标降低。因此，为更精确分析孤岛运行对负荷点可靠性指标的影响，需要考虑随机变量的不确定性和相关性。

对比分析表5 各种情况下系统可靠性指标可得：

1）对比本文方法情况1～情况4：DG 接入系统后，SAIFI 值由情况1 的5.238 4 升至情况2、情况3、情况4 的5.6 左右，ASAI 值略微上升，其他系统可靠性指标均呈下降状，即系统平均停电频率上升但停电时间下降，供电可用率上升。对比情况2与情况3，可得DG 的不确定性使系统孤岛运行期间供需波动较大，系统的可靠性指标略微劣化。对比情况3 与情况4，情况4 的系统可靠性指标优于情况3，虽然光伏孤岛内负荷点可靠性指标劣化，由于风机出力波动远比光伏出力要小，风机孤岛2改善负荷点的可靠性指标程度要大于光伏孤岛1 劣化程度。随机变量的不确定性及相关性通过影响负荷点的可靠性参数，进而影响系统可靠性指标。

2）情况4 下对比不同方法计算结果：文献[11]方法计算结果优于本文方法，但由于未考虑孤岛持续时间，因此孤岛对系统可靠性指标改善作用更为理想，而本文考虑孤岛运行时间td计算可靠性指标更符合实际情况。文献[5]方法计算结果劣于本文方法，由于未考虑孤岛内源-荷不确定性，仅利用修正参数对传统可靠性指标计算公式进行修正，其计算结果主要取决于修正参数的选择，而本文方法充分考虑了孤岛内的源-荷不确定性，结果更为精确。

3）与文献[12]交流配电网可靠性参数比较，直流配电网的可靠性明显劣于交流配电网，主要因为直流配电网引入了各种可靠性水平较低的直流设备。随着电力电子技术的发展，直流设备的可靠性不断提高，未来直流配电网的可靠性指标可能会接近交流配电网。

附 录

1. 直流变压器可靠性模型

本文对DAB-ISOP 型直流变压器建立马尔科夫模型，其拓扑结构如附图1 所示。

附图1 DAB-ISOP 型直流变压器拓扑结构App.Fig.1 Topological structure of the DCSST

DAB-ISOP 型直流变压器由多个DAB 单元以高压侧串联、低压侧并联的方式连接组成。每个DAB 部分由高压侧电容器、高压侧全桥模块、电感器、高频变压器、低压侧全桥模块和低压侧电容器六个部件组成，任意一个部件发生故障都会导致整个直流变压器故障。基于此，对DAB 单元进行马尔科夫可靠性建模，状态转移过程如附图2 所示。

附图2 直流变压器的马尔科夫状态转移图App.Fig.2 Markov state transition diagram of DCSST

5 结论

本文建立了综合考虑设备可靠性、孤岛内源-荷的不确定性、相关性及孤岛持续时间的直流配电网可靠性评估模型，通过算例分析得到以下结论：

1）本文对各直流设备建立的马尔科夫可靠性模型考虑了设备的运行状态及冗余度，更符合实际情况，有效地描述了直流设备的可靠性。

2）DG 的接入能够缩短计划孤岛内负荷点的停电时间、提高系统可靠性水平。

3）在含DG 的直流配电网中，随机变量（风速、光照强度和负荷）之间的相关性对计划孤岛内负荷点和系统的可靠性均有影响，同时考虑DG 及负荷的不确定性和随机变量间的相关性使得评估更符合系统的运行实际。

4）采用多场景技术能有效地模拟随机变量的不确定性，孤岛内源-荷不确定性会影响孤岛运行时段内的供需平衡，综合考虑孤岛源-荷的不确定性和孤岛持续时间的孤岛形成概率可以量化DG 对直流配电网可靠性的影响，计算结果更为可靠。

附图 2 中，状态 0 为系统正常运行，状态i(i=1,2, …,6)分别表示直流变压器的六个部件发生故障导致系统发生故障。通过维修故障部件，系统状态可以从故障状态转移到正常运行状态。λi、μi(i=1,2, …,6)分别为高压侧电容器、高压侧全桥模块、电感器、高频变压器、低压侧全桥模块和低压侧电容器的故障率、修复率。根据状态转移图可得直流变压器的状态转移密度矩阵为

参考前述换流器的马尔科夫可靠性建模方法，根据状态转移密度矩阵可以列出直流变压器的 Chapman-Kolmogorov 方程，设初始状态后可以解方程组得到直流变压器的可靠度函数及故障率。

2. 直流断路器可靠性模型

直流断路器在直流配电网中主要起到隔离故障的作用。目前，学者们对于直流断路器的拓扑研究主要集中在三种类型：机械式直流断路器、固态直流断路器和混合式直流断路器。其中，混合式直流断路器结合了前两种断路器的优点，可靠性高、寿命长、通态损耗小，因此最具有大规模商业化应用的前景，为各方研究的重点。

混合式直流断路器的拓扑结构如附图3 所示，主要由超快速机械开关（Ultra-Fast Disconnector，UFD）、电流转移开关（Load Commutation Switch，LCS）、主断路器单元、避雷器构成，其中，主断路器单元由n个IGBT模块串并联而成。对直流断路器进行马尔科夫可靠性建模，状态转移图如附图4 所示。

附图3 混合式直流断路器的拓扑结构图App.Fig.3 Topological structure of the hybrid DC circuit breaker

附图4 混合式直流断路器的马尔科夫状态转移图App.Fig.4 Markov state transition diagram of the hybrid DC circuit breaker

附图4 中，状态0 表示直流断路器正常运行，其余状态表示因不同的部件故障而导致整个直流断路器发生故障。通过维修故障部件，系统状态可以从故障状态转移到正常运行状态。λ i、μi(i=1,2,3,4)分别为超快速机械开关、电流转移开关、主断路器单元、避雷器的故障率和修复率。由此可得直流断路器的状态转移密度矩阵为

同样，可以通过求解方程及设定初始状态得到直流断路器的可靠度函数、故障前平均工作时间及故障率。

储能设备的容量和充放电功率模型为