基于单管电路的恒流恒压无线充电系统研究

王春芳 岳 睿 李厚基 李 聃

（1. 青岛大学电气工程学院 青岛 266071 2. 青岛鲁渝能源科技有限公司 青岛 266071）

0 引言

感应式无线电能传输技术以其安全稳定、使用方便、电气与机械隔离等优点，在研究中越来越受青睐[1-4]。它可工作在水下、矿井等恶劣环境中[5]，同时也被广泛应用于无线供电和电池充电等领域，如LED 照明[6]、人工心脏供电[7]、手机电池的无线充电[8]、电动汽车的无线充电[9]等。在给电池充电的过程中，需要对电池进行先恒流后恒压的充电控制[10-11]。

利用无线电能传输（Inductive-Power-Transfer,IPT）实现恒流输出（Constant Current Output, CCO）和恒压输出（Constant Voltage Output, CVO）的方法可分为以下四类：①在无线接收端增加一个DCDC 变换器[12-13]，通过闭环控制实现CCO 和CVO；②利用拓扑本身特性单独实现 CCO[14-16]或单独实现CVO[17-18]；③用混合拓扑结构[19-20]通过改变辅助开关管的工作状态，在不同充电时刻切换为不同的补偿拓扑来实现CCO 和CVO；④在特定的补偿网络下通过切换开关频率的方式实现CCO 和CVO[21-22]。

第④种方法中所述的拓扑结构没有引入额外的直流变换器和额外的功率开关管，既节省了电路设计成本，也使控制策略得到简化。文献[21]提出了一种由双边LCC 补偿网络构成的全桥逆变IPT 系统，通过将开关频率由fCC切换至fCV，可使系统实现由恒流模式到恒压模式的转换。其一次线圈自感为16.18μH，二次线圈自感为15.52μH，耦合系数k=0.367。当增大传输距离到k降为0.2，且维持一次、二次线圈电感量不变时，电路的最低开关频率为3.2MHz。为了降低开关频率需要增加线圈的电感量，当一次、二次线圈的电感量均增加为100μH 且维持k=0.2 时，系统的最低开关频率为517kHz。在该双边LCC 补偿网络下为进一步降低电路开关频率，需要进一步增加线圈的电感量，这使得该补偿网络难以应用于小功率输出领域。且由于单管电路结构的特殊性[23]，传统的双边LCC 补偿网络不能应用于单管电路，否则当开关管关断时，一次侧补偿电感将会失去放电回路，所产生的电压尖峰将会损坏开关管。

为了解决上述问题，本文提出了一种基于单管电路（Single-Switch Circuit, SSC）的恒流、恒压补偿拓扑P-CLCL，同样可以通过切换开关频率实现由CCO 到CVO 的切换。且相比于全桥双边LCC 补偿网络结构，P-CLCL 的参数计算过程被大幅简化，在用相同的松耦合变压器的情况下，单管P-CLCL补偿网络的开关频率远低于双边LCC 补偿网络的开关频率，且由于只有单个开关管，其具有可靠性高、成本低、结构及控制策略简单等优点。但如果只依靠开环恒流、恒压拓扑本身的特性，并不能实现完全意义上的恒流恒压输出。因此，有必要引入闭环控制，进一步调控输出电流和电压。本文从电路的互感等效模型出发，分析给出了基于该补偿拓扑的参数计算方法，进行了等效输入电压波形的傅里叶分解以求取输入波形基波幅值，给出了一种利用“Mathcad”软件画图迭代拟合求取一次侧补偿电容的方法，设计了一种基于无线通信模块的闭环调频控制。最后，本文搭建了一台25.2W 的IPT 充电系统样机，对所提P-CLCL 补偿拓扑进行了开闭环实验验证。

1 P-CLCL 补偿拓扑的分析

图1 给出了基于单管电路P-CLCL 补偿拓扑的互感等效模型，CP为一次侧补偿电容，LP为一次线圈电感，LS为二次线圈电感，M为一次与二次线圈间的互感，iLP(t)为一次线圈电流，IBAT与VBAT分别为输出电流、输出电压，VDC为直流供电电源。

图1 基于单管电路的P-CLCL 补偿拓扑Fig.1 Single-switch IPT with P-CLCL network

图1 中，C1、L1、L2、C2构成了二次侧CLCL补偿网络。为了对图1 所示电路进行原理性分析，将电感L1分解为L11和L12，且采用松耦合变压器的互感等效模型，使图1 化简为如图2a 所示单管P-CLCL补偿拓扑的互感等效模型。图2 中，V˙in为单管电路等效输入电压源的基波值，图2b 为将图2a 进一步用戴维南定理化简后的结果。

图2 单管P-CLCL 补偿拓扑的互感等效模型Fig.2 Mutual inductance equivalent model of P-CLCL compensation network

1.1 恒压输出模式分析

假定当电路工作在频率fCV下时，电路将有恒压输出特性。由图2b 可知，当等效电感LS-M2/LP与电容C1在频率fCV下谐振时，将是一个与负载无关的电流源，图3 所示为恒压输出模式下的戴维南/诺顿等效电路。

图3 恒压输出模式下的戴维南/诺顿等效电路Fig.3 Thévenin’s and Norton’s equivalence in CVO mode

若C2与L2也在频率fCV下谐振时，则与负载无关的电压源将与负载Req并联，恒压输出。因此，当要求有恒压输出特性时，电路应满足

式中，ωCV为恒压工作下的谐振角频率。

而在全桥拓扑中，需要满足式（2）以同时实现全桥中4 个开关管的软开关和恒压输出特性[21]。

显然，由于引入了额外的参数限制条件，这将大大增加计算量和计算过程的复杂性，而在单管电路中，由于软开关可以通过设计一次侧补偿电容CP的值来实现，无需引入额外的限制条件，有助于简化计算过程。

因此，如图3 所示，在恒压输出模式下电路的输出电压计算式为

式中，V˙in的大小为输入交流电源电压峰值。显然，当松耦合变压器的值和输入电压确定时，恒压输出电压值只与开关频率fCV和补偿电容C2有关。

1.2 恒流输出模式分析

恒流输出模式下的戴维南/诺顿等效电路如图4所示。假定当电路工作在fCC频率下时，电路将有恒流输出特性。当T 网络具有图4 中T1的结构时，其输出可等效为一与负载无关的恒压源[24]。

图4 恒流输出模式下的戴维南/诺顿等效电路Fig.4 Thévenin’s and Norton’s equivalence in CCO mode

此时，角频率ωCC和T1网络的输出电压应满足

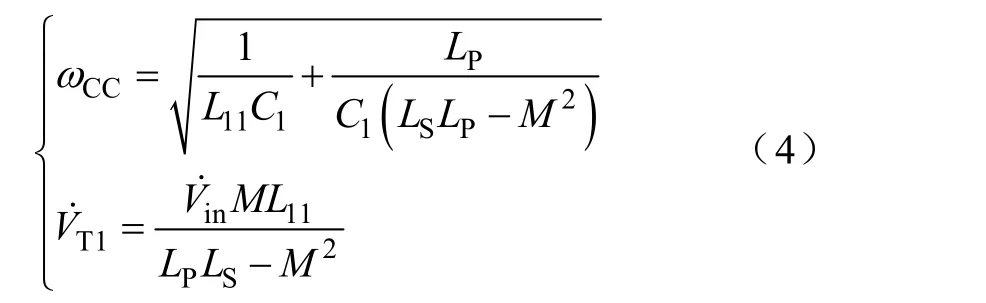
由戴维南定理可得，T2网络的输入电压源可被转化为图4 所示的电流源。如果设计L12和C2在频率fCC下谐振，则与负载无关的电流源将与负载Req串联，输出为恒流输出。因此，当要求有恒流输出特性时，电路应满足

因此，如图4 所示，在恒流输出模式下电路的输出电流可计算为

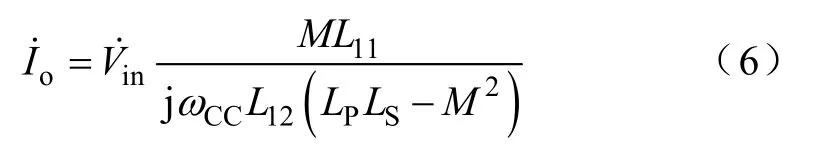
显然，当松耦合变压器的一次、二次侧自感、互感和输入电压确定时，恒流输出的电流只与开关频率fCC和补偿电感L1有关。

为了计算补偿网络P-CLCL 的参数，现引入一个角频率关联因子α，并假定ωCV=αωCC。因此，联立式（1）～式（4），可得参数L11计算式为

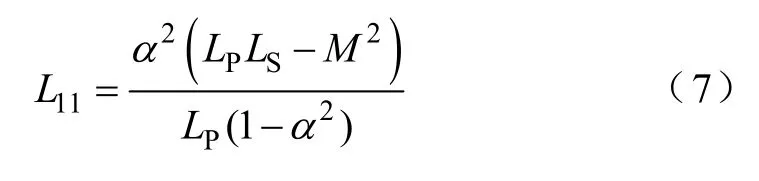
将式（5）、式（7）代入式（6），则恒流模式下的输出电流为

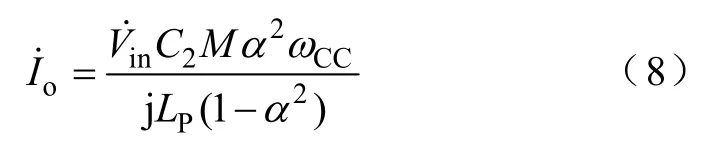
由式（3）、式（8）的输出电压和输出电流模值可得

为了便于参数的设计，可先给定ωCC的值。再由式（9）求得α和C2的值，进而由式（1）和式（5）求取P-CLCL 补偿网络的其他参数为

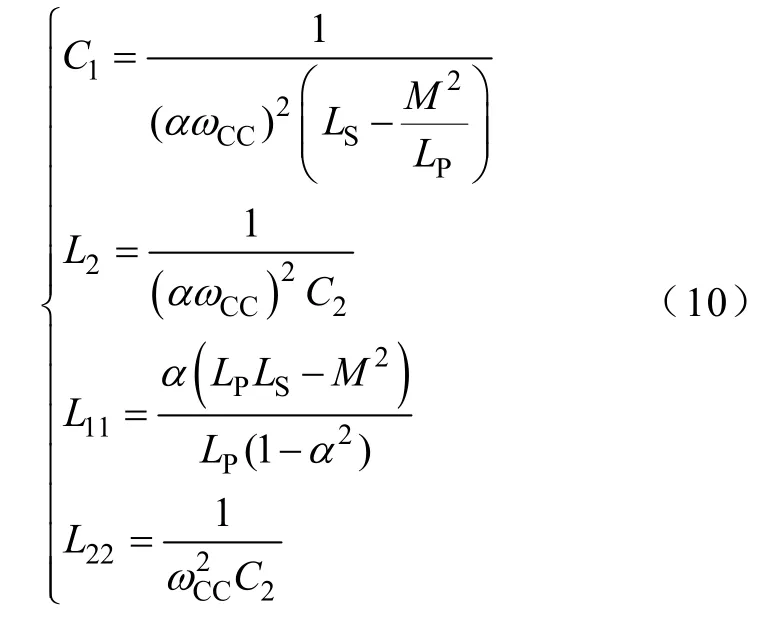
2 单管逆变电路等效输入电源的求解

图1 所示的单管逆变电路结构，其一次侧补偿电容CP两端的电压波形为整个补偿网络的供电电压波形，即为等效输入电压源的波形。其形成过程为：当开关管工作在正向和体二极管反向导通状态时，电容CP的电压值将被钳位为输入电源电压值；当开关管工作在截止状态时，电容CP的电压波形将由谐振网络决定，且其欠阻尼谐振峰值为A，单管电路等效输入电源波形如图5 所示。

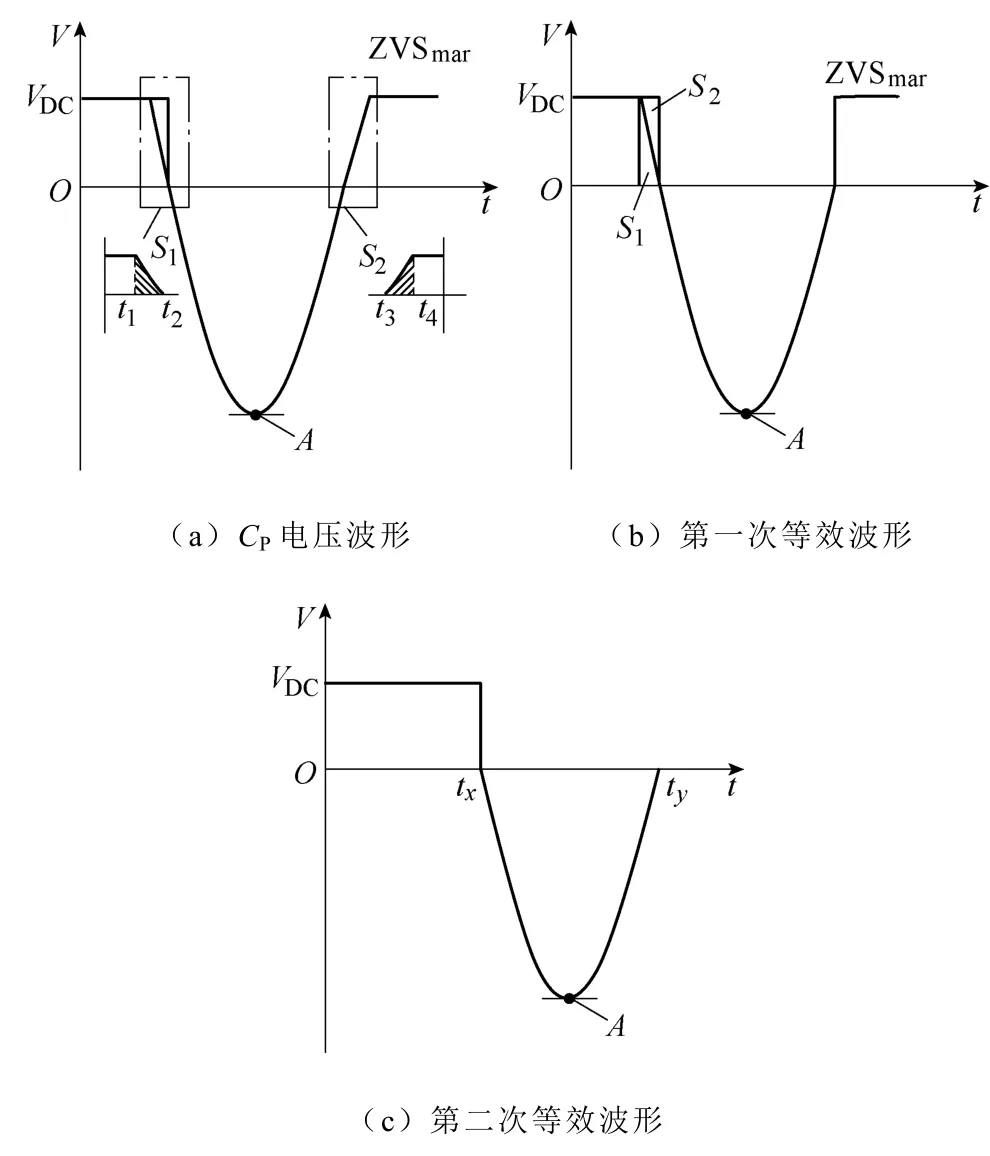
图5 单管电路等效输入电源波形Fig.5 The waveforms of equivalent input power source in single-switch circuit

为了便于分析，在开关管关断时，用正弦波代替CP中的谐振电压波形，并选取t2点作为时间起始点。因此，谐振电压波形的表达式可写为

图5a 中，当工作周期设为T，占空比设为D，

软开关裕度（ZVS margin）写为ZVSmar时，ω′为

现对图5a 作如下处理：将ZVSmar所示的t5-t4时间段，移至t1-0 时间段。合并t4-t3时间段的电压波形与x轴所围成的面积S2和t2-t1时间段的电压波形与x轴所围成的面积S1使其成为一个矩形，如图5c 所示。则vCP(t)的分段函数为

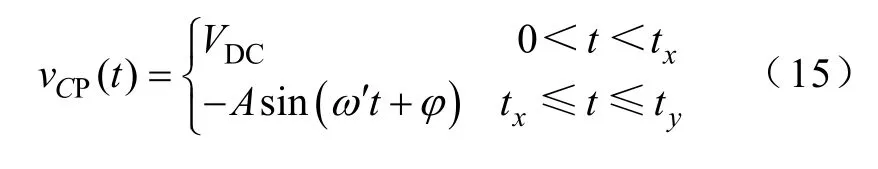
其中

由于式（16）的方程左右两边均为关于A的函数，无法直接根据式（16）求解得到A的值。因此，可令式（16）等号左右两个表达式为两个不同的以A为变量的函数P1(A)、P2(A)。利用“Mathcad”绘图工具求解P1(A)和P2(A)的交点，即可得A的值，CP谐振峰值的求解如图6 所示，图中，输入电压为32V，故可算得开关管耐压峰值为86V+32V=118V。

图6 CP 谐振峰值的求解Fig.6 Solution of resonance peak value in CP

图 5 所示的等效输入电源波形不是规则的波形，需要对其进行傅里叶分解以求取基波幅值。求解式（15）所示分段函数的基波幅值共有两种方法：①用Saber、PSIM 等仿真软件的傅里叶分解工具获取该波形的基波幅值；②使用傅里叶分解公式，手动求解基波幅值A1，即

当输出采用如图1 所示的整流桥和一个电容Co滤波时，滤波前后的电压与电流值[21]应满足

式中，Io、Vo为整流滤波前交流电流及电压峰值。

将式（17）的基波峰值A1和式（18）代入式（3）、式（8）、式（9），得到电路的输出电压、输出电流、α、C2的表达式为

3 一次侧补偿电容CP 的设计

为了分析计算CP的值，图1 所示电路应简化为图7，并规定了电容电压和电感电流的正方向（见图7）。图中，RL和Leq分别为恒流模式下，输入电源总阻抗Ztotal的实部和虚部，其值可由图2a 计算为

图7 图1 的简化电路Fig.7 The simplified circuit of Fig.1

图8a 和图8b 分别给出了单管逆变电路在正常工作状态及临界工作状态下的工作过程波形。显然，当开关管开通时，CP的电压将被钳位在VDC，当电路工作在图8b 所示的工作状态时，iLP(t)的状态方程可写为

图8 工作过程波形Fig.8 Waveforms of the operation states

需要注意的是，图8b 所示的工作状态是一种临界工作状态。当开关管导通时（如时间点t7），iLP(t)反向过零并开始增加，因此iLP(t)的初值为0。由图7 可知，当开关管开通时，VDC将给Leq充能，充能时间为DT；当开关管关断时，CP、Leq和RL将会发生零输入响应，uCP(t)和iLP(t)的状态方程可写为

在t6时刻，电容CP两端的电压达到VDC，电感电流iLP(t)将通过开关管的体二极管续流。此时电路的状态方程为

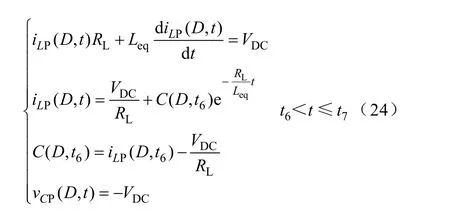
至此一个工作周期结束，在t7时刻电路将进入下一个工作周期。然而上述推导的状态方程只适用于如图8b 所示的临界工作状态。正常情况下电路均工作于图8a 所示的状态，其中t4-t1＞T，在t3时刻开关管开通时iLP(t)的值小于零。由于当电路工作在这种工作状态下时，式（22）中开关管开通时刻的iLP(t)初值iLP(DT)难以确定，因此也就难以列写如式（21）～式（24）所示的状态方程，随之也就无法根据求解零输入响应的时间求取CP的值。因此，下文给出了一种利用“Mathcad”软件图像迭代求取CP的值的方法。

分析图8 可知，对于单管电路，改变开关管的占空比不会影响CP上谐振电压的波形。这是因为早在开关管的体二极管导通时，开关管就已视为导通，与开关管的驱动信号是否到来无关，调节占空比只会改变软开关裕度ZVSmar。在输入电压确定的情况下，图5 中谐振峰值A将会是一个定值。

因此利用“Mathcad”图像求取CP值的步骤为：

（1）给定输入电压为VDC，占空比为D，软开关裕度为ZVSmar，欠阻尼谐振峰值为A，利用式（20）计算出RL及Leq的值（本文中，D=0.5，ZVSmar=8%，fCC=100kHz）。

（2）任意给定一个CP的值，用“Mathcad”画出式（22）中vCP(t)的波形，并手动修改iLP(DT)的值，使得图像中的谐振峰值等于-A（本文为-86V）。

（3）若设软开关裕度为0.08T，则根据图8，应使CP的谐振波形在(1-D-0.08)T时达到电源电压值。因此，要观测在步骤（2）中所设CP的值和iLP(DT)的值是否能够满足步骤（3）的要求。

（4）重复进行第（2）步和第（3）步，使得CP的谐振波形在(1-D-0.08)T时达到电源电压值，同时满足谐振峰值等于-A。最后CP的谐振电压波形如图9 所示。

图9 CP 的谐振电压波形Fig.9 The resonance waveform in CP

步骤（1）～步骤（4）的工作流程如图10 所示。采用此种方法，可以算得CP=80nF，考虑到现有CBB电容的规格，选为CP=82nF。

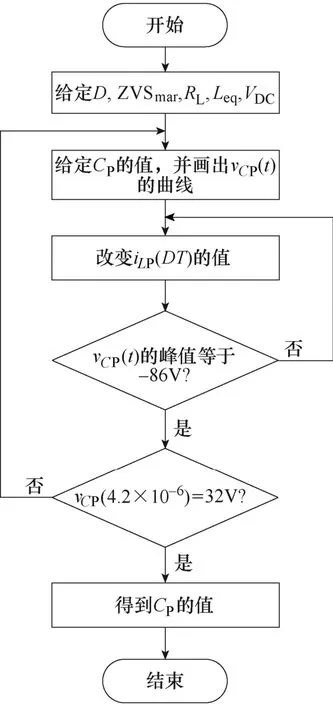
图10 电容CP 的设计流程Fig.10 The design flow chart of CP

然而CP的容值也可以由仿真软件直接仿真分析得到：在计算得到二次侧CLCL 补偿网络的所有电路参数之后，只需手动更改仿真中CP的容值，使得软开关裕度能够满足预期值即可，此时的CP容值即为满足设计需求的值。与手动计算相比，此方法更为简单快捷。

4 实验验证

为了验证上述分析，本文搭建了一台恒流输出为1A，恒压输出为25.2V 的实验样机，分别在阻性电子负载和锂电池（5 200mA·h）为负载的情况下进行实验验证。电子负载时的实验平台如图11 所示。其中，锂电池采用6 串2 并的结构，其单体电压为3.7V。当电池充满电时单体电压为4.2V，锂电池总体端电压为6×4.2V=25.2V。

图11 电子负载时的实验平台Fig.11 Experiment platform with electronic load

实验中设定直流输入电压VDC=32V，占空比D=0.5，软开关裕度ZVSmar=8%，恒流模式下的开关频率fCC=100kHz。任意绕制一次线圈LP=15.82μH，二次线圈LS=15.34μH，互感M=3.48μH（耦合系数k=0.223）的松耦合变压器。将由式（10）、式（19）算得的二次侧CLCL 补偿网络参数见表1。

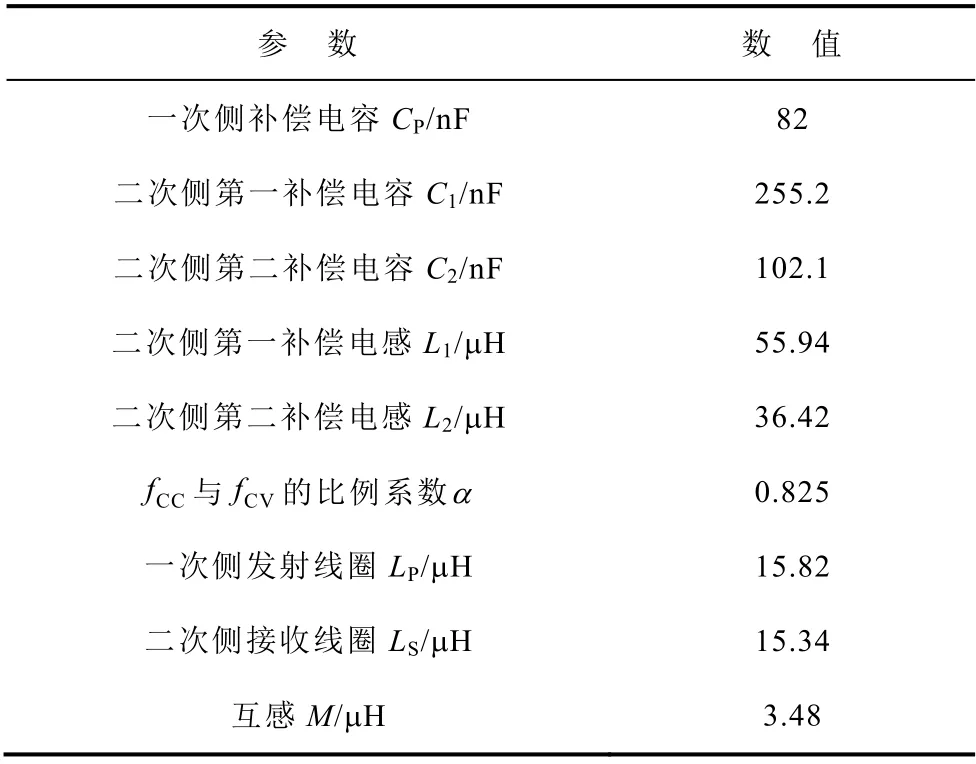
表1 单管P-CLCL 谐振电路参数Tab.1 Single-switch P-CLCL resonant circuit parameters

图 12a、图 12b 分别给出当电子负载阻值为25.2Ω 时在开环恒流模式和开环恒压模式的软开关波形及软开关裕度波形。图中，ΔX为ZVSmar所占时间。

图12 零电压软开关波形Fig.12 Waveforms of ZVS

如图12 所示，在恒流模式下，软开关裕度ZVSmar=(780/1000)×100%=7.8%，近似等于本文设计要求的8%，且其开关管电压峰值123V，近似等于由第2节所推导出的开关管电压峰值118V。实验值与理论值的差是因在器件选择过程中，器件实际参数与理论计算参数间的偏差导致的。理论推导与实验结果的一致性证实了上述推导结论的正确性。

为了验证电路的恒流恒压输出特性，图13 给出了开环恒流模式与恒压模式切负载实验波形。

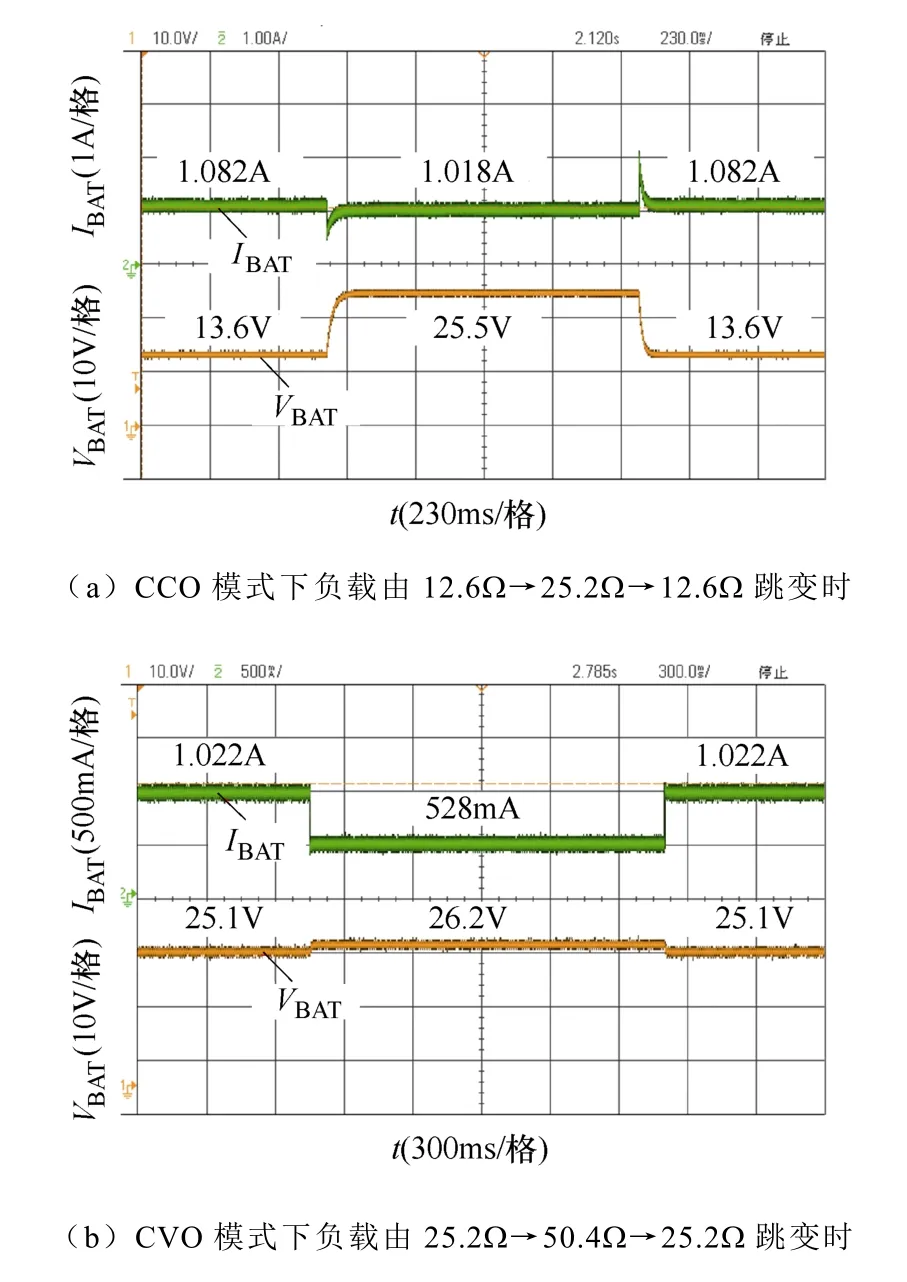
图13 负载跳变时开环输出电压电流波形Fig.13 Output waveforms when the load leap in open-loop

由图13a 的开环波形可知，当电路工作在恒流模式下时，即使负载在半载和满载间跳变，输出电流基本保持不变，而输出电压跳变为原来的2 倍，实现了恒流输出的特性。当电路工作在图13b 所示的恒压模式下时，负载在额定负载与额定负载的两倍之间跳变时输出电压基本不变，输出电流变为原来的1/2。开环实验证实了该电路具有良好的恒流输出特性和恒压输出特性。

图14 给出了闭环恒流模式与恒压模式切负载实验曲线。其中，闭环调频控制策略如图15 所示。

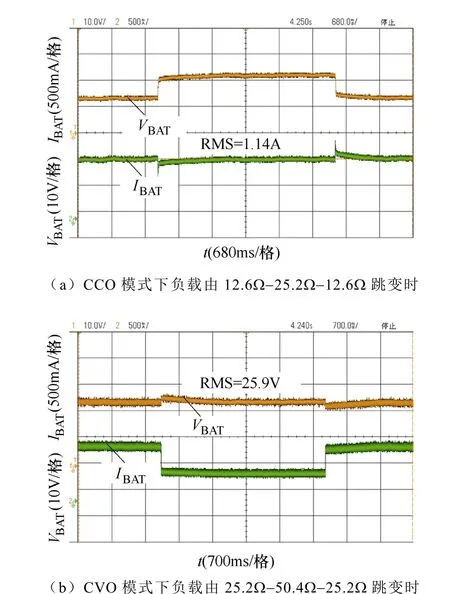
图14 负载跳变时闭环输出电压电流波形Fig.14 Output waveforms when the load leap in closed-loop

图15 闭环调频控制策略Fig.15 Closed-loop frequency modulation control strategy

由图14a 可知，在引入闭环后，负载跳变时，闭环控制系统总能将输出电流稳定在恒流输出额定值；由图14b 可知，在引入闭环后，负载跳变时，闭环控制系统总能将输出电压稳定在恒压输出额定值。其中，实验值与理论值的差是因在器件选择过程中，器件实际参数与理论计算参数间的偏差导致的。

将此电路用于电池充电时，虽然恒压模式下负载变化时，输出电压跳变不大，但它也已经超出了锂电池所要求的电压充电范围。有必要引入闭环调频控制，进一步精细调控输出电压。图16a 给出了在没有引入闭环时锂电池充电曲线，其中恒流输出设定为1A，恒压输出设定为24V，其松耦合变压器与本文所用一致，电路参数见表2。图16b 给出了用nrf24l01 无线通信模块进行一次、二次侧电路通信的闭环锂电池充电曲线。

图16 锂电池充电曲线Fig.16 Charging curves of lithium battery

表2 输出24V/1A 时补偿网络参数Tab.2 The parameters of compensation network when the output is 24V/1A

显然，从图16a 可看出，在不引入闭环的情况下，由于在充电过程中电池的端电压逐渐上升，当锂电池端电压上升至25.2V 时，为了安全起见需要断开充电电路，而此时充电电流只降为0.57A，这导致电池的电量无法充满。由图16b 可知，在恒流充电阶段充电电流保持稳定，电池端电压呈近似线性上升趋势。在恒压充电阶段充电电压保持稳定，电池的充电电流迅速下降。在充电的第315min 时，充电电流下降为0.12A，充电结束。该实验结果证实了所引入的调频控制的可行性及可靠性。

不同电子负载阻值和工作模式的开环效率曲线如图17 所示。

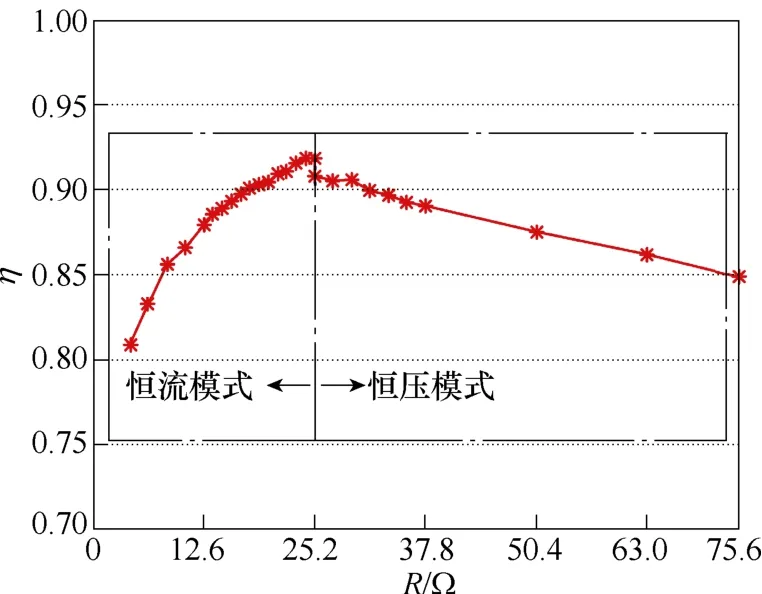
图17 效率曲线Fig.17 Curve of efficiency

当电路工作在恒流模式下，且其负载为25.2Ω时，可以达到最大的输出效率0.929。由Pout=I2R可知，当在恒流阶段，负载增大时，系统输出功率变大，则系统损耗相对降低，导致负载增大时效率也随之上升，恒压阶段则与之相反。由恒流模式转变为恒压模式时的效率突变是由于改变频率后，一、二次线圈上流经的电流增大，导致在线圈内阻上的功耗增加所造成的。

5 结论

单管逆变电路具有结构简单、可靠性高、成本低、体积小、质量轻、控制精度高等一系列优点，但一直无法通过切换开关频率实现恒流充电模式到恒压充电模式的转换，导致该电路的应用受到局限。为解决这个难题，本文构建了一种新型P-CLCL 补偿网络，给出了详细的参数计算分析方法。并通过开闭环实验证实了本文理论分析的正确性，拓展了单管电路的应用领域。本文的设计方法亦可推广至其他类型的单管电路（如Class-E 电路）的设计分析上。