基于声波时域特征的锂离子电池荷电状态表征

张 闯 孙 博,2 金 亮,2 刘素贞,2 杨庆新,2

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2. 河北省电磁场与电器可靠性重点实验室（河北工业大学） 天津 300130）

0 引言

根据美国先进电池联合会给出的定义，荷电状态（State of Charge, SOC）是电池在一定放电倍率下，剩余电量与相同条件下额定容量的比值[1]。它反映了锂离子电池的续航能力，已经成为新能源汽车电池管理系统（Battery Management System, BMS）中的主要监测指标之一[2]，也是动力电池组能量均衡的重要判据[3]。对SOC 的有效估计有助于实时获取剩余电量，准确地掌握电池工作状态，以及可靠地选择充电策略[4-5]。

锂离子电池SOC 表征技术一直是国内外的研究热点之一。根据测量原理，目前锂离子电池的SOC 表征方法主要基于电学参数[6-7]、热学参数[8]和声学参数[9]三类。其中，基于电参数的表征技术多以等效电路模型为基础，并结合数据驱动的方法实现SOC 估计，其短期估计误差小，但是计算成本高。此外，由于电参数方法无法直接反映电池内部结构老化对SOC 的影响，其长期累积误差依然较大。利用热学参数的估计往往不能与SOC 构成单一的映射关系，通常与电参数联合估计才能实现表征。依据声学参数的表征方法以电池的本体结构特征演变规律为基础，对SOC 的变化较为敏感，在电池状态评价和内部结构失效方面具有显著优势。

由于超声波可以检测材料构件中气泡、裂纹、夹杂异物等缺陷，并进一步判断材料的疏密、弹性模量、厚度等特性的变化，因此近年来超声技术主要应用于电池内部产气、电解液浸润情况、电池状态等领域的检测中。国内外学者对锂离子电池的超声检测研究主要集中于电池内部主要不同工况下电化学过程引发的副反应[10-11]、电池状态[12]和内部材料的分布特征[13]表征等方面。B. Sood[14]等对超声检测技术在锂离子电池健康状态（State of Health, SOH）监测的应用进行了初步探索，证明该技术具有检测锂离子电池内部结构特征的能力。文献[15]对电池内部力学本构关系进行数值模拟，证实影响SOC 与SOH 的动力学特性主要是材料的密度与杨氏模量，为声学方法在电池状态检测中的应用奠定了理论基础。锂离子电池中声学-电化学耦合的构效关系是多对多关系，如何从声学测量的实验结果中，唯一地解释某一种动力学特性变化的原因，还需要大量的基础研究。

当前基于声学参数对锂离子电池状态研究较少，主要采用常规的声学时域指标来表征。J. B.Robinson 等[16]通过分析超声信号幅值的变化来判别由嵌锂和脱锂引起的电极材料密度变化，结果表明充电过程中阳极与阴极密度变化随SOC 呈相反趋势。P. Ladpli 等[17]基于超声信号幅值、飞行时间（Time of Flight, ToF）建立了SOC、SOH 的预测模型，取得了较好的预测效果。文献[18]通过对比充放电过程中ToF 的变化趋势，分析了电极结构的动力学特性变化规律，并指出电极材料的杨氏模量与SOC 和外加电流具有相关性。W. Chang[19]等通过建立声学-电化学耦合模型，从宏观角度利用超声纵波测量出电池的整体有效刚度。由于电池的电化学、动力学过程涉及复杂的多物理场耦合问题，当前针对锂离子电池的动力学特征与电池状态的对应关系研究仍处于探索阶段，锂离子脱嵌过程引起的杨氏模量的规律性研究还不够深入。常用的声波时域指标中，信号幅值的测量容易受耦合剂、压力等影响且不同声波下的变化特征不统一，ToF 的获取计算量大、对硬件采样精度的要求高。此外，由温度等外界实验条件产生的实验结果变化显著[20]，需要规范实验过程降低实验误差。

针对上述问题，本文在现有研究方法基础上，引入声波振铃计数，设计了基于声学时域特征的锂离子电池SOC 在线检测方法。在恒温条件下，对正常工况下的商用钴酸锂（LiCoO2, LCO）离子电池进行循环充放电实验和超声信号处理；基于振铃计数描述电池整体有效杨氏模量对SOC 的依赖性，建立短期循环中二者之间的对应关系，并进行锂离子电池SOC 超声检测实验；结合幅值和ToF 偏移量归纳锂离子电池的短期循环动力学特性，并验证振铃计数对SOC 表征的可行性。

1 声学指标表征SOC 机理

本文以软包锂离子电池为研究对象，从超声检测机理和参数表征原理两个方面进行阐述。

1.1 锂离子电池荷电状态声学检测机理

单体锂离子电池充放电原理示意图如图 1 所示，单体电池内单电极单元主要由正极、负极、隔膜、集流体、电解液组成，将多电极单元经卷绕或折叠等工艺制成。以正极材料是LCO 的锂离子电池为例，在充电过程中，锂离子在层状结构的石墨材料和层状结构LCO 材料的层间嵌入和脱出，电极发生的化学反应为

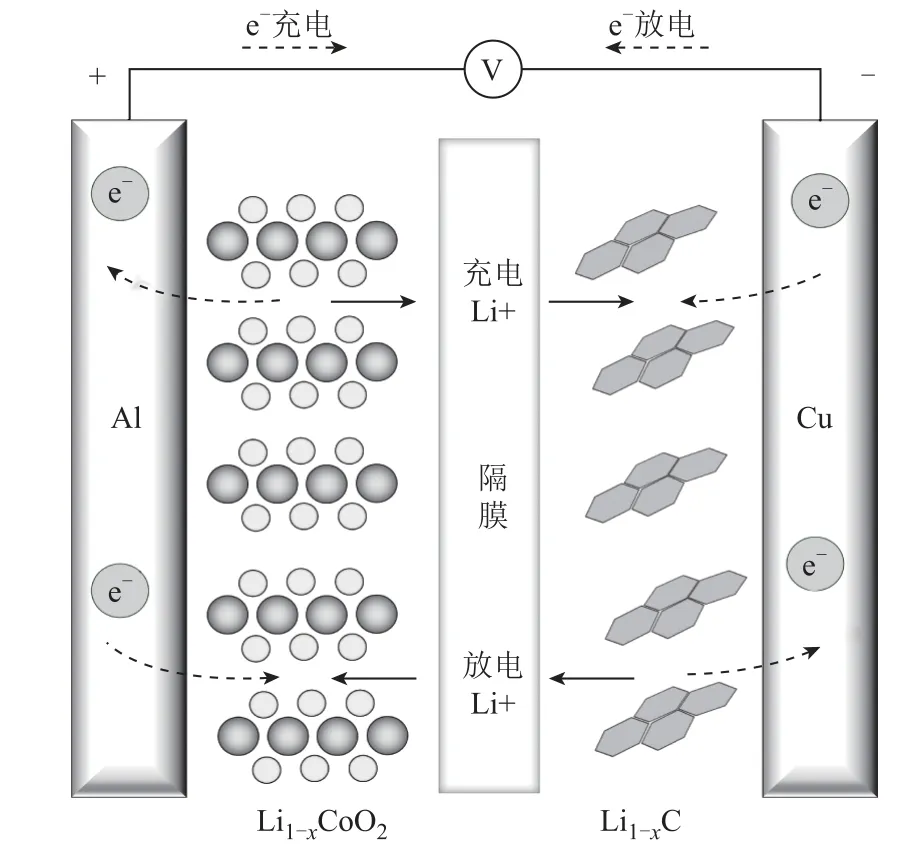
图1 单体锂离子电池充放电原理示意图Fig.1 Charging and discharging principle of single lithium ion battery

在电化学领域，SOC 表示锂离子电池电极颗粒中包含的电荷量，它的变化反映了锂离子在电极颗粒中的浓度分布[22]。可见，锂含量与电池SOC、电极杨氏模量均具有直接关联的关系，因此锂离子电池的电化学-声学耦合关系被建立起来。

纵波在电极中的传播速度取决于波所经过的介质的物理性质。描述纵波波速与动力学特性关系的方程为

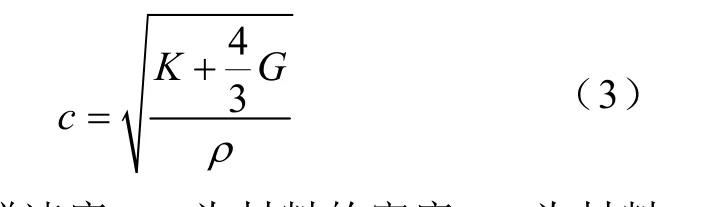
式中，c为纵波群速度；ρ为材料的密度；K为材料的体积模；G为材料的剪切模量。而K和G均与材料的杨氏模量E和泊松比ν相关，关系为

可见，材料的密度和杨氏模量共同决定了声速的大小。经半电池测试发现，声速主要由阳极模量、阳极密度和阴极密度三个因素决定[14]。

常见用于表征SOC 的声学指标有声波幅值和ToF，这两种指标表征原理为

式中，Z为电池整体声阻抗；t为声波传播时间；l为电池厚度。由于声阻抗变化影响了声波在介质中的衰减程度，导致接收波的能量改变，因此声阻抗的变化会影响声波的幅值。由于锂离子电池属于多层多相介质，声阻抗和衰减的建模计算仍是一项难题，目前未有完善的数学建模与求解方法[15]。但从以上公式可以看出，声波幅值、声传播时间均受到杨氏模量和材料密度的影响。

可见，在电化学-声学耦合关系中，若想独立分析杨氏模量对声学传播特性的影响，选取一个对该动力学特性具有强敏感性的声学指标尤为重要。

1.2 振铃计数与电池整体有效杨氏模量的关系

在无损检测领域，振铃计数通常用于声发射检测技术中裂缝产生和扩展的表征，能初步反映信号强度和频度, 通常用于材料内声发射活动性评价。本文引入振铃计数这一概念，在基于超声纵波的锂离子电池SOC 检测实验中，提取该特征参数用于对电池内部结构变化的评估。

根据Lemaitre 的应变当量原理，检测试样损伤本构模型可表示为

式中，σ为应力；ε为应变；D为损伤变量，试样未受损时D=0，试样完全受损时D=1。

由于随着循环次数的增加，锂离子电池结构趋于疏松，表现为在纵向深度方向产生微小膨胀。假设纵向深度初始截面为A，循环充放电过程中第i级加载时，纵向膨胀深度截面为Ad，则损伤变量Di为

式中，β为耦合系数。当试样整个截面完全膨胀变形时，采集到的总累计声发计数为Nm，则单位膨胀面积内计数No为

电池测试模块主要由新威高精度电池性能系统提供，包括下位机（CT-4008-5V6A-S1）和中位机（CT-ZWJ-4′S-T-1U）。电池选用3 435mA·h 软包锂离子电池（SP376080SI，天津力神），正极材料为钴酸锂，负极材料为石墨，尺寸为80mm×60mm× 3.76mm。锂离子电池充放电工步设置参数见表1。

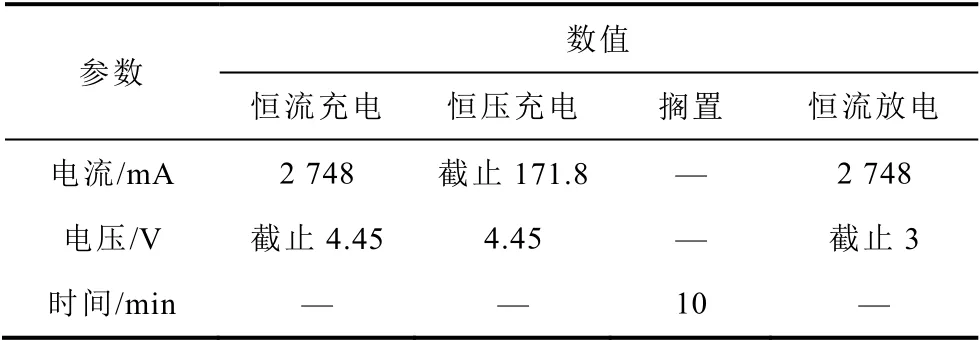
表1 锂离子电池充放电工步设置参数Tab.1 Setting parameters of charging and discharging step of lithium-ion battery

式（15）即为振铃计数与杨氏模量之间的映射关系表达式。Nm通常可在电池失效下获得，与电池材料、尺寸等有关，在检测对象不变时可看作常数。作为式（15）中的关键参数，获取的动态振铃计数Ni在一定程度上避免了电池整体有效密度变化对该参数的影响，且电极的锂化和脱锂化而产生的应力仅与充电倍率有关[19]，因此在单一充电策略下可以通过振铃计数分析杨氏模量与SOC 之间的关联关系。电化学-声学耦合模型中主要变量对应关系如图2 所示。

图2 耦合模型主要变量对应关系Fig.2 Correspondence of main variables in the coupling model

2 锂离子电池SOC 的超声检测实验

2.1 实验平台的搭建

本文提出的锂离子电池SOC 在线检测实验平台主要由电池测试模块、主机控制模块、恒温控制模块和超声检测模块组成。该实验平台的结构如图3 所示，其工作原理为：电池测试模块将电池以特定充电机制循环充放电；在充放电的同时触发超声测量模块，超声测量模块采用一发一收模式，从而测量由电池纵向深度方向接收到的超声纵波；将电池及夹具整体置于恒温箱内，以降低由温差影响产生的实验误差。

图3 锂离子电池SOC 超声检测实验平台示意图Fig.3 SOC ultrasonic test platform for lithium-ion battery

为保证电池充满，在恒流充电后需进行恒压充电，使锂离子在电极材料中达到均匀分布。由于锂离子电池厚度较薄，为避免由于波长过大引起的波的叠加，以及保证波的传输效率，选取频率为5MHz的压电探头（A405A-SB，日本奥林巴斯）以激发和接收透射波。在换能器与电池接触表面涂有油性耦合剂（B2 甘油耦合剂，日本奥林巴斯）以增强波传输效率，维持长时间的在线测量。利用夹具固定压电探头的位置，利用置于探头和夹具之间的压力传感器测量压力以保证夹具施加的压力一定，锂离子电池检测装置实验图如图4 所示。

图4 超声检测装置实验图Fig.4 Experimental drawing of ultrasonic testing device

2.2 实验数据的获取和处理

根据图3 搭建的锂离子电池SOC 在线测量平台如图5 所示。恒温箱温度设定为25℃，对锂离子电池进行60 次的循环充放电，已知该电池使用寿命为300 次，由此可认为60 次循环内为短期循环特性分析。超声模块施加经汉宁窗调制后的单周期正弦波信号，夹具对探头施加3N 的压力，单次充放电循环时长约为4h，利用PC 端对示波器接收到的信号每4min 保存一次，根据现有研究，纵波在正极为LCO的锂离子电池传播速度约为2 250m/s，因此接收到初至波时间约为2μs 左右，初至波完整波包时长约为5μs，调节示波器获取波形窗口时为8μs 左右。

图5 实验平台实物Fig.5 Physical picture of the experimental platform

将获取的实验数据首先进行平滑去噪处理，以滤除实验过程中由恒温箱、测试仪等引起的环境噪声产生的声信号。再进行去趋势处理，以消除传感器在获取数据时产生的偏移对幅值的量值和振铃计数阈值选取的影响。

3 声学指标的提取和分析

3.1 常规声学指标的提取

单循环周期内SOC 两极值（SOC=0 和1）下的波形对比如图6a 所示。不同SOC 对应的声波幅值差异显著，这说明锂离子在两个电极之间转移时，晶格结构相应变得强硬和弛豫，进而影响材料的阻尼及其衰减特性。通常情况下，更坚硬紧凑的材料具有更低的材料阻尼，能量衰减越少。因此SOC 较高时，阳极锂含量越高，衰减越小，幅值越大。

图6 SOC=0 与SOC=1 波形对比Fig.6 Comparison of SOC =0 and SOC =1 waveform

同时在声传输时间上有明显偏移。由于电池平均声速近似为电池整体有效杨氏模量与密度之比的二次方根，SOC 越高时该比值越大，声速越大，接收到信号时间越短。因此本文采用传统的声学指标为幅值和ToF 偏移量。其中，幅值取为信号的希尔伯特上包络的最大幅值，飞行时间偏移量取为波形包络线的幅值与基准波形幅值之间的时间差值，其基准波形为测试过程中第一次记录的波形（开路状态下），计算公式为

式中，t1为测试波形包络线幅值最大值对应的时刻；t基准为电池开路状态波形包络线幅值最大值对应的时刻。指标提取示意图如图6b 所示。

3.2 振铃计数的提取

锂离子电池组成主要由固相和液相两部分组成，简化电极结构，可以看成是固体骨架内充满了电解质。根据Biot 理论，波的能量损失是由于粘性的孔隙流体和固体骨架之间的相互作用。因此波在锂离子电池内部的传播中衰减特性值得注意。从图6a 中可以看出，SOC=1 时刻对应的波形较SOC=0 时衰减过程长。本文提出振铃计数的原理是通过设定阈值来统计信号超过阈值的次数，利用这个计数来表达结构的阻尼特性。

图7 描述了振铃计数的提取过程。声波在锂离子电池内传播中，一部分被反射，一部分经折射被换能器接收，在折射过程中由于材料的粘滞性以及其他阻尼特性所带来的能量损失是波衰减直至消失的主要原因。部分反射波在电极层内被多次反射，经折射后被传感器接收，该现象在多激励周期下可被明显捕捉。由于本实验采用激励时间短，信号微弱且不与主波包重叠，设其主波包的方均根（Root Mean Square, RMS）的10%为阈值电压，未超过阈值的波包将被滤除以针对主波包的计数提取，超过阈值信号的振荡次数则设为每组数据的振铃计数。

图7 振铃计数的提取Fig.7 Extraction of ringing count

3.3 数据分析

3.3.1 电池首次循环数据分析

经过信号处理，锂离子电池初期循环中振铃计数随SOC 变化规律如图8 所示。从电压曲线可以看出电池首次充电时间较短，这是由于电池购买后放置一段时间使用，使得电池进入休眠状态，此时容量低于正常值，首次充放电是对电池进行激活的过程。由于锂离子电池“无记忆性”，首次自然充电不会对后续容量产生影响，但由于处于激活过程，其对应时刻幅值数据杂乱无章，无明显趋势，说明此时锂离子电池内部未形成新的平衡态，电极结构不稳定。从第二次开始，其充放电特性恢复正常。

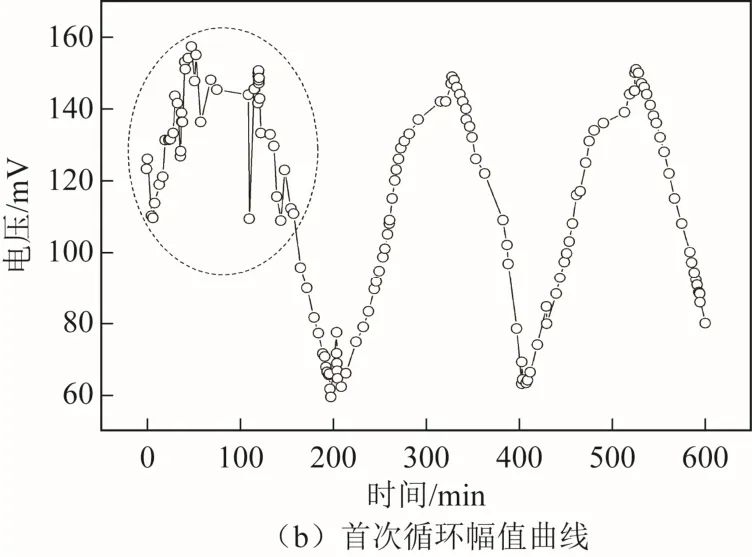
图8 首次循环数据对比Fig.8 Comparison of first cycle data

3.3.2 电池短期循环数据分析

经信号处理，图9a 展示了第3～11 个循环周期下，以振幅为例的电参数-声学参数对应曲线。在前60 次的早期循环中，超声波形具有可重复的趋势，并呈周期性变化，且与电化学循环同步。因此对于SOC 的表征研究，选取具有代表性的一个周期数据进行具体分析。

图9 初始循环充电数据对比Fig.9 Comparison of initial cycle charging data

充电过程中，振铃计数主要显示出阶段性特征，分为平稳期、上升期和下降期。不同阶段振铃计数对应的电化学状态不同，根据锂离子电池的工作原理，单次循环中影响振铃计数的因素可归纳为：①可循环锂离子浓度；②锂离子分布均匀度；③充电机制。由于杨氏模量与SOC 存在内在联系，导致不同SOC 对应的振铃计数变化规律存在差异，针对振铃计数的不同演变时期进行分析。

充电过程中，首先对电池进行恒流充电，锂离子电池内部发生大量的正极脱锂和负极嵌锂。充电初始，对于电池来说，因为突然施加大电流激励，电池端电压会有一段阶跃升高过程，这是由快速的电极反应使电极表面液层内反应离子的浓度迅速变化导致的，即浓差极化。而此时振铃计数与幅值ToF偏移量一样，显示出短暂的快速衰减现象。充电中期，振幅和ToF 偏移量变化趋势平稳，这说明浓差极化得到了抑制。而此时振铃计数在充电中期几乎保持平稳，可见此时锂离子电池整体有效密度不断升高，而杨氏模量的变化微小，不足以影响到计数的变化。充电后期，电压达到阈值改为恒压充电，由于锂离子浓度分布不均而在其内部极容易产生较大的内阻，即欧姆极化效应。为了改变这种分布不均，给电池施加一个恒定的电压以避免电压虚高。由于电极材料的电化学刚度在充电中期升高、充电后期降低[18-19]，振幅和ToF 偏移量的变化率在该充电机制转换中发生了改变，最终导致振幅在充电中期增长率小、后期的增长率大，ToF 偏移量在充电中期衰减、在充电后期增加。但从实验数据可以发现，振幅的增长率变化不明显，ToF 偏移量变化存在延迟，说明这两种指标表征充电机制转换过程时并不灵敏。从图9b 中可以看出，此时振铃计数处于上升期，表明电池内部杨氏模量变化明显，可见电流逐渐减小导致的密度变化差异对声传播特性影响权重降低。其中，相关系数（R2）用于表示拟合曲线和实测曲线的线性相关程度。计数可以唯一地表示与杨氏模量的对应关系，进而将杨氏模量的变化趋势凸显出来。

放电过程中，采用恒流放电模式，电极经历相反的电化学过程。初始循环放电数据对比如图10 所示。此时振铃计数整体呈下降趋势，由于放电采用单一模式，从振铃计数和幅值可以看出，其整体有效杨氏模量对SOC 有较强的依赖性，电池整体有效密度与杨氏模量均随SOC 的减少而降低。这可以解释为在锂离子从负极脱锂时，电极内的交换电流密度变化产生的结果[23]。交换电流密度可以用来描述电化学反应的严重程度。因此放电阶段，电极内锂离子浓度逐渐降低，进一步电解所需的动力学阻力就越大，此时声阻抗越大，接收到透射波的频度和强度均减弱，计数逐渐减少。此外，通过对比图9 和图10 可知，声波计数、电压、幅值、ToF 偏移量曲线中充电数据与放电数据不完全重合，称为锂离子电池的迟滞现象，而迟滞特性是由于锂脱嵌产生的扩散应力引起的，这也说明声学时域特征能够描述锂离子电池的材料属性，从充电和放电实测数据可以看出，振铃计数实际变化不会均匀增加或均匀下降，而是呈阶梯性浮动，这也体现了在电池充放电循环过程中，若性能完好无明显损伤（鼓包、断裂等），在电池的服役过程中其动力学特性演变较为平缓。

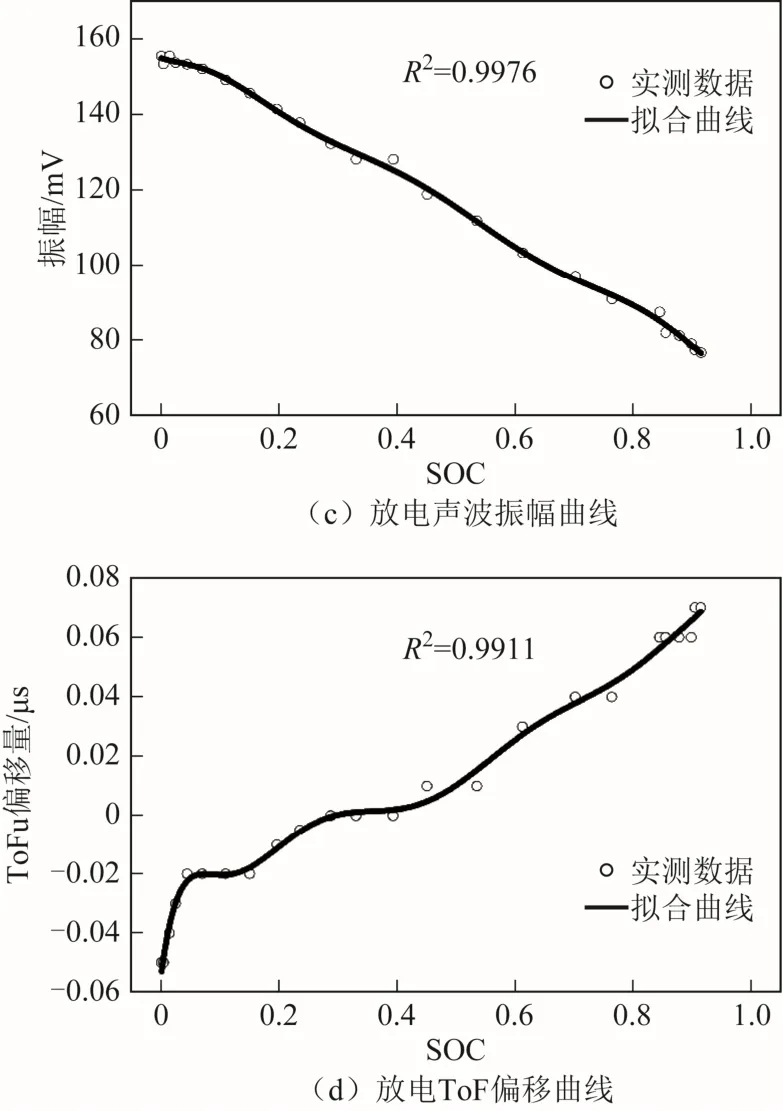
图10 初始循环放电数据对比Fig.10 Comparison of initial circulating discharge data

通过对比充放电过程中振铃计数与常规声学指标随SOC 的变化规律可以得出，由于振铃计数与杨氏模量唯一的对应关系，在充放电过程中不仅可以展示出常规声学指标的表征功能，还能进一步详细地揭示杨氏模量的演变规律，这是常规的声学指标所不能体现出来的独特优势。在充放电过程中随着SOC 的变化，在充电后期根据振铃计数变化可以得出杨氏模量与SOC 呈接近线性相关。但是由于振幅和ToF 偏移量指标整体变化存在非单调性，计数在充电中期也存在平稳期，因此在实际中通常采用多个声学指标的融合估计。

3.3.3 多特征声学指标的融合估计

为了说明引入计数指标对表征精度等方面的优势，本文基于高斯过程回归对不同指标下SOC 的估计误差进行了对比。高斯过程回归适用于小样本且非线性的数据的估计。该原理是建立在贝叶斯框架下，并且模型性质由均值函数和协方差函数确定，其中协方差函数（即核函数）类型的好坏直接决定了最终预测精度的大小。本文选取的核函数为平方指数型协方差函数，其预测过程为：将给定的样本数据集通过预处理提取得到声学指标，并分为测试集和训练集。训练集用来训练高斯过程回归模型，最后用测试集对模型进行测试，并根据测试结果分析预测的效果。高斯过程回归预测流程如图11 所示。

图11 高斯过程回归预测流程Fig.11 Gaussian process regression prediction flowchart

图12a 为采用振幅与ToF 偏移量指标对SOC 的估计结果。图12b 为采用振幅、ToF 偏移量与计数指标的估计结果。通过图12a 和图12b 的对比可以看出，增加计数指标可以降低由于振幅和ToF 偏移量所产生的估计偏差，尤其是在充电前期和充电后期。

图12 多特征声学指标估计精度对比Fig.12 Comparison of estimation accuracy of multifeature acoustic indexes

为了能够更全面地评价引入计数指标后的预测精度，本文采用平均绝对误差（Mean Absolute Error,RMAE）及相关系数（R2）作为评判标准，其定义为

基于声学指标对SOC 估计精度对比见表2。可以看出引入计数指标后，RMAE从0.065 下降至0.016，且R2从0.864 提升到0.952。因此能够得出，声波时域特征不仅可以描述大部分的电化学循环过程，且多特征声学信息对SOC 的融合估计也能够有效地提升估计精度。

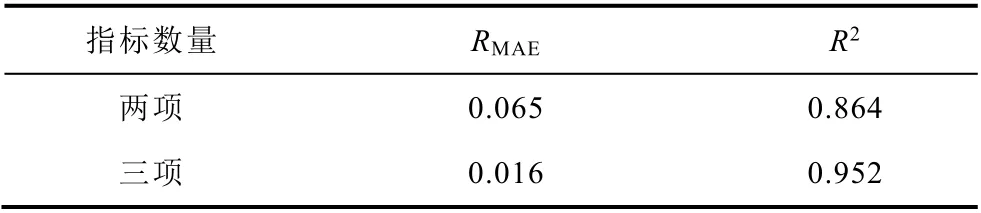
表2 估计精度对比Tab.2 Comparison of estimation accuracy

3.3.4 不同放电情况超声计数特性分析

电极结构的老化对电池的各种状态均会产生影响，老化程度越深，电池电能存储能力越弱，SOC衰减得越快。在电池内部，老化通常是由于电化学循环过程带来的副反应产物（如锂金属镀层、气体、固态电解质界面膜等）的出现，引起了结构的膨胀和疏松，在动力学特征上体现为杨氏模量的降低，相应地导致了声阻抗特性的变化。因此基于声学信号表征电池SOC 时，可以体现电池内部结构老化对SOC 的影响。

在相同循环次数下，温度、倍率等因素与电池的老化直接相关[24]。本文获取了循环次数为50 次的不同循环倍率、不同温度下的电池放电过程中计数数据，并绘制拟合曲线如图13 所示。温度相同时，更快的充放电倍率增强了锂离子浓度分布的不均匀性，进而加速了电池的老化。倍率相同时，更高的温度下锂离子的扩散率更大，相同循环次数时更容易诱发副反应产物的产生，进而加速了电池的老化。这两种情况最终均会导致相同SOC 下电池的稳定性更差，即电池维持电量的能力减弱。而在电化学过程中，体现为锂离子浓度的迅速衰减以及副反应产物的产生。与前文提到的浓差极化现象类似，锂离子浓度的降低将导致声波幅值变弱，副反应产物的声阻抗与电极材料本身的不匹配程度致使波在界面层之间来回反射，削弱了声波的能量，在获取的透射波信号上强度与频度均被减弱，计数的平均水平降低。由图13 可知，相同循环次数下，在温度为25℃、放电倍率0.8C时，超声计数最高，而更高的放电倍率或更高的温度，都将导致超声计数降低。因此，实验数据验证了计数在不同放电情况下表征SOC 的可行性，同时也反映了电池结构老化对SOC的影响。

图13 不同放电情况的计数对比Fig.13 Comparison of counts for different discharge conditions

本文针对锂离子电池早期循环的声响应特性进行了阐述，建立了声学指标与SOC 之间的对应关系，进行了相关的定性分析，给出了初步的估计精度。然而电池SOC 的在线表征和估计常常面临更复杂的实际工况，如环境温度的变化、动态电流的波动等。若想获取更为精准的SOC 估计值，对声学参数的鲁棒性提出了更高的要求。此时，丰富的历史数据和有效的预测模型必不可少。若外界环境温度改变，需要在算法中给予一定的温度补偿。若遇到复杂工况，则需要及时地对模型参数进行辨识和修正。必要时，需要多特征参数的融合才能更准确地获得实时的估计结果。因此，有效的声学指标是获取精准表征结果的重要前提。

此外，不同循环周期中表现出可重复性规律，虽然周期与周期之间声学指标变化很小，但这些微小的变化表明声学特性与电池的老化特性存在强相关性，或者可以用来表征锂离子电池的SOH，这表明通过超声计数、幅值、ToF 偏移量等指标的融合分析，可为锂离子电池失效提供可靠的先兆信息。因此，未来有必要深入开展基于循环周期间声学指标差异的电池老化状态与健康状态评估研究。

4 结论

本文搭建锂离子电池SOC 在线检测平台，通过信号处理，引入振铃计数参量，结合常规时域指标对锂离子电池整体有效杨氏模量规律演变进行分析，并进行了锂离子电池SOC 表征研究，得出以下结论：

1）推导了振铃计数于杨氏模量之间的对应关系。根据基于Lemaitre 应变等效原理推导出的对应关系可以体现振铃计数唯一地揭示整体有效杨氏模量的演化规律的能力。

2）获得了锂离子电池整体有效杨氏模量变化规律。基于SOC 与杨氏模量、振铃计数之间的对应关系，根据振铃计数变化趋势的可以得出锂离子电池杨氏模量单次循环中总体表现出“稳→升→降”的趋势和阶梯性变化特征。实验结果表明，超声计数可以体现电池结构老化对SOC 的影响，该指标在电池健康状态与剩余寿命评估方面具有巨大的应用潜力。

3）初步实现了基于声波时域特征的锂离子SOC表征。从实验数据可以看出，杨氏模量在充电后期与SOC 呈近似线性的对应关系，基于高斯过程回归法对SOC 的估计误差对比发现，计数指标的增加可有效提升表征精度。因此，超声计数与幅值、ToF 偏移量相结合可以对锂离子电池SOC 进行有效表征，为锂离子电池短期循环特性的可靠判定提供参考依据。