基于对抗式迁移学习的含柔性高压直流输电的风电系统次同步振荡源定位

陈 剑 杜文娟 王海风,

（1. 新能源电力系统国家重点实验室(华北电力大学) 北京 102206 2. 四川大学电气工程学院 成都 610065）

0 引言

近年来，随着新能源电力系统规模的不断扩大，风机的装机容量不断提升，柔性高压直流输电（Voltage Source Converter based High Voltage Direct Current Transmission, VSC-HVDC）凭借其快速灵活的调节能力、与弱交流电网互联的方便性以及不存在换相失败等诸多优势得到了广泛应用，经VSCHVDC 并网已成为风电场等分布式电源采用的最有效的并网方式[1-3]。

然而，风电场经VSC-HVDC 并网可能引发振荡不稳定事件，广东南澳风电场经柔性直流并网工程、德国北海海上风电经柔直并网工程，以及云南鲁西柔性直流输电工程均曾发生过宽频振荡事件[4]。已有研究证明，风电场并网时风电机组与外部接入系统的动态交互容易导致系统失稳，如文献[5]研究单风机与弱电网的动态交互作用以及交互作用引起的振荡稳定性；文献[6]研究多风机多换流器之间强交互作用对系统稳定性的影响；文献[7]指出风机与HVDC 也存在动态交互的风险。因此，风电汇集外送系统存在次同步振荡的风险，且已经成为威胁系统安全稳定运行的关键因素。为了抑制风电场振荡保证系统安全稳定运行，定位风电场次同步振荡源是迫切需要解决的实际问题。

目前，关于振荡源定位的研究主要分为两类。一是基于机理分析的数值仿真方法。如文献[8]提出暂态能量流计算方法，通过在汽轮发电机组多质量块详细模型下推导能量流的组成说明次同步振荡中暂态能量流和阻尼的关系，并根据计算网络中的振荡能量流和能流功率定位扰动源。文献[9]提出基于分流系数的次同步振荡源定位方法，通过分析次同步频率分量的传播路径，与实际系统中通过监测装置得到的次同步电流的分布规律对比，根据差异确定振荡源。从现有的基于机理分析的次同步振荡源定位方法来看，能量函数法或其衍生的方法在低频振荡源定位方面取得了较为成功的应用[10-11]，但由于次同步振荡的频率范围宽，诱发机理复杂，关于次同步机理的研究尚存在不足，低频振荡源定位的相关方法在次同步振荡源定位方面的普适性还有待进一步考证。

二是基于数据驱动的方法。数据驱动方法是更面向工程实际的方法，也是实现无参数建模最为有效的方法。文献[12]提出基于阻抗法的振荡源定位方法，通过相量量测单元（Phasor Measurement Unit,PMU）获得节点数据，并采用阻抗法计算等效阻抗并判断是否为振荡源。然而，等效阻抗的计算与谐振点的准确度有很大关系，且阻抗法严重依赖快速傅里叶变换（Fast Fourier Transfer, FFT）或Prony 算法等频率分析方法，导致该方法定位精度不高且处理速度过慢。因此，文献[13]针对次同步振荡（Subsynchronous Oscillation, SSO）的定位提出基于数据的能量流方法，通过对低频振荡的能量流方法进行推广，该方法不需要构造能量函数，通过量测数据计算系统的总能量与振幅，从而判断消耗能量的元件对振荡衰减的贡献。然而，该方法虽然能够在某些特定的算例下得到正确结论，但其适应性有待进一步验证。

此外，在基于数据驱动的方法中，机器学习方法是近几年新兴的方法，如文献[14]通过对PMU 量测的振荡信号采用多分类器集成学习方法确定量测信号与振荡源位置标签的关系模型，实现扰动源定位。文献[15]提出基于平滑伪Wigner-Ville 分布图像和深度迁移学习的方法，通过图像转换与模型迁移的方法实现振荡源定位。然而，目前深度学习在电力系统中应用的最大挑战是，现有的模型对仿真系统更有效，而仿真系统得到的模型能否适应实际系统是亟待解决的问题。因此，文献[16]提出基于特征迁移的方法，在含直驱风机风电场系统中进行了振荡源定位的初步验证分析，其采用最大均值差异对仿真系统和实际系统的量测数据进行分布度量，然而，这种度量方式存在核函数高度非线性化的劣势，在定位模型的优化计算方面仍存在较大的不足。

鉴于此，本文针对大规模风电场经VSC-HVDC接入电力系统而发生次同步振荡的场景，研究将对抗式迁移学习方法用于振荡源定位。该方法通过对仿真系统与实际系统的样本进行对抗学习，缩小仿真系统与实际系统的域差异，相比于传统深度学习该方法将会更适应于实际电力系统，从而为实际系统中的风电场次同步振荡源在线定位提供了一种解决思路。

1 基于特征的深度迁移学习方法

1.1 深度迁移学习

迁移学习[17]是将一个领域内学习到的知识应用到另一个相似的领域中去，即采用机器学习算法将已有知识从源任务迁移进目标任务。迁移学习和深度学习密切相关。迁移学习的目标是关键因素的泛化，这也是深度学习的目标，即开发具有鲁棒性的学习模型并具备指导迁移的能力。而迁移学习与传统深度学习的不同之处在于，迁移学习目标是泛化不同样本集合之间的共性，而深度迁移学习则是侧重于样本之间的共性，其示意图如图1 所示。

图1 迁移学习示意图Fig.1 Schematic of transfer learning

假设用于学习的数据样本划分为源域Ds和目标域Dt，且任意数据域都由其特征空间X及概率分布P(X)构成。对于源域与目标域内的任务（学习目标）由标签空间和预测函数f(x)组成，记为Ts={Ys,fs}和Tt={Yt,ft}。其中，Ys与Yt分别表示源域和目标域的标签空间，fs与ft分别表示源域和目标域的映射函数，或条件概率Qs(Ys|Xs)和Qt(Yt|Xt)，即f(x)=Q(Y|X)。如果源域与目标域的数据特征完全一致，此时利用源域数据学习到的任务，迁移到目标域中也能适应目标域中的任务。但实际上，由于源域与目标域的特征是不可能完全一致的，从数据分布来说主要体现在两个数据域系统的边缘分布与条件分布不同，因此，迁移学习就是利用两个域的数据样本，通过优化的方法找到能够使两个域的学习任务均达到最优的学习。为了更好地描述上述问题，给出数学定义为：给定有标签源域Ds={(Xs,Ys)}={(x1,y1),…, (xn,yn)}，与无标签目标域Dt={(Xt)}={xn+1,…,xn+m}, (x∈Xs,y∈Ys)，并且满足Xs=Xt,Ys=Yt,Ps(Xs)≠Pt(Xt),Qs(Ys|Xs)≠Qt(Yt|Xt)，迁移学习即学习预测函数ft:xt→ yt使其在目标域上的泛化误差最小。则，由＜Ds,Dt,Ts,Tt,ft(·)＞确定的学习即为迁移学习，假设其中预测函数ft(·)是深度表征函数，即为深度迁移学习。

稳态运行数据充足，而振荡失稳数据相对匮乏且价格昂贵是电力系统数据不平衡的典型特征。为了克服系统数据样本的不平衡状态，仿真系统成为电力系统分析的重要手段，因此，传统的深度学习大部分的做法是利用同一个仿真系统获取数据样本进行训练与测试，而采用迁移学习的目标是在仿真系统中训练得到的模型能够实现泛化到实际系统中。深度特征表示的目的是提取不同系统数据域间的不变结构，从而保证训练模型具有较强的泛化性，因此，本文提出采用含有特征提取器的对抗式网络用于仿真系统与实际系统的不变特征学习，从而建立次同步振荡源定位的深度学习模型。

1.2 对抗式的特征迁移原理

由于仿真系统是由实际系统做了诸多假设而得到的理想系统，因此，仿真系统与实际系统差异较大，那么，从两个系统中获得的数据域也存在较大差异。为了解决上述问题，采用特征迁移的方法通过在抽象的特征空间中量化差异并缩小该差异。设仿真系统为源域，实际系统为目标域，其中源域是有标签的系统，记为Ds={(X1,Y1),…,(Xn,Yn)}；目标域是无标签系统，记为Dt={Xn+1,…,Xn+m}。对于基于特征的迁移学习方法，实际上是从源域与目标域中学习一对映射函数{φs(·),φt(·)}，实现源域与目标域数据映射到公共特征空间，而对抗式迁移学习模型是采用对抗式网络获得这个公共特征空间。将源域与目标域中的数据映射到公共特征空间之后，迁移学习便可以利用两个域的数据来训练模型。

为了实现域不变的特征迁移学习，Y. Ganin 等提出域对抗的神经网络（Domain-Adversarial Neural Network, DANN）来学习域不变特征[18]作为可供迁移的特征。该网络由三个子网络构成：①在域间共享的特征提取器（F）；②用于源域分类的标签分类器（C）；③域判别器（D）。其网络结构如图2 所示。

图2 DANN 结构示意图Fig.2 Structure of DANN

图2 中，特征提取器和标签分类器构成了一个前馈神经网络，而特征提取器与域判别器构成了反馈神经网络，通过一个梯度反转层连接。该网络首先将数据映射到特定的特征空间，然后通过调整网络参数使标签预测器输出的损失最小化，以及域判别器输出的损失最大化，从而获得域不变特征。因此，该网络的损失由标签分类器损失Lscls和域判别损失Ld两部分构成。

标签分类器损失Lscls由特征提取器与分类器两个子网络的输出构成，表示为

式中，GC为标签分类器的输出函数，选择Softmax作为激活函数；GF为特征提取器的输出函数，(Xsi,Ysi)表示源域第i个样本。

同理，域判别器损失Ld表示为

式中，GD为以Sigmod 函数作为激活函数的域判别器的输出；bi为第i个样本属于源域或目标域的二元标签，bi={0,1}。

因此，为了提取源域与目标域的不变特征，需要标签预测器与域判别器不断对抗式更新网络参数，从而使标签预测器的输出损失最小，域判别器的输出损失最大[19]，即

式中，W、v分别为提取器网络的权重及偏置参数；b、c为标签预测器参数；u、z为域判别器参数；E表示期望；上标“∧”表示更新值。

虽然DANN 目的是最小化源域分类误差项和最大化域分类误差项，但整体目标函数是最小化问题，因此在域分类误差项前加了负号，并且引入超参数λ作为权重平衡参数[19]，则，该网络的优化目标函数可表示为

式中，ns、nt分别为源域数据样本和目标域样本数量；F、C、D分别为特征提取器、标签分类器、域判别器的参数。

最终计算求得网络参数即为对抗式迁移网络参数，将该网络应用到目标任务从而在实际系统中对振荡源进行识别定位。

2 风电场经VSC-HVDC 并网的振荡源定位深度学习模型

2.1 风电场经VSC-HVDC 并网的振荡源诱发机理

风电场经VSC-HVDC 接入交流电网的结构示意图如图3 所示，其中风机通过风电场交流拓扑网络汇集到公共耦合点PCC，经过整流换流器、高压直流输电线路和逆变器注入交流系统。风电场侧整流换流器与风电场直接相连，控制目标是维持风电场出口节点的交流母线电压恒定。

图3 风电场经VSC-HVDC 并网结构Fig.3 Structure of wind farms connected to the power system via VSC-HVDC

为研究风电场次同步振荡的诱发机理，将图3 风电场系统中每个风电场用一台风机等效，在某一运行点下，风电场系统的线性化状态空间方程表示为

图3 系统中，除风电场系统外，含VSC-HVDC 的部分称为剩余子系统，剩余子系统状态空间方程[20]表示为

式中，ΔYw为输入变量，由风电场向剩余子系统的注入功率构成；ΔVw为输出变量；Ad、Bd、Cd、Dd分别为剩余系统系数矩阵；ΔXd为剩余系统状态变量，由剩余子系统所有状态变量构成。

将式（6）和式（7）写成传递函数形式，即

式中，H(s)为风电场的前馈子系统传递函数矩阵；G(s)为剩余系统的反馈子系统传递函数矩阵。

联立式（6）～式（9），可得全系统闭环互联模型，如图4 所示，风电场经VSC-HVDC 并网系统的闭环状态方程表示为

图4 风电场经VSC-HVDC 并网闭环互联模型Fig.4 Closed-loop interconnection model of wind farms connected to the power system via VSC-HVDC

式中，As为全系统的闭环特征矩阵。

风电场系统与剩余系统构成一个互联系统，系统稳定性由开环子系统稳定性及其闭环互联系统稳定性所决定。当ΔVw=0，图4 所示互联系统开环，此时，系统稳定性由开环子系统稳定性所决定。系统的开环模式包括风电场开环子系统的开环振荡模式λw（矩阵Aw的特征值）和剩余子系统的开环振荡模式λd（矩阵Ad的特征值）。当ΔVw≠0 时，说明风电场系统与剩余子系统之间发生动态交互过程，系统处于闭环状态。此时，系统的闭环模式包括第j个风电场的开环模式λwj对应闭环模式λˆwj和剩余系统的第i个开环模式λdi对应的闭环模式λˆdi，则开闭环模式变化可表示为Δλw=λwˆj-λwj，Δλd=dˆiλ-λdj。根据开环模式谐振理论[21]可知，当两个系统的开环模式接近时，即λdi≈λwj（记为系统第k个特征根λsk，对应矩阵As的特征值），两个系统可能发生强烈的动态交互，由于λwj是H(s)的极点，λdi是G(s)的极点，则当两个系统开环模式接近时，闭环系统的传递函数可能会非常大，使得反馈环节对前馈环节的影响增大，从而引起系统振荡失稳。

已有研究证明，当风电场中风电机组数目增多可能会增强风电机组与VSC-HVDC 送端换流器的相互作用，引发次同步振荡[22]。因此，及时确定参与交互的风电场，并在发生振荡时减少该风电场的运行机组，能够尽快平息振荡。考虑振荡的诱发是由于风电场参与交互，因此，将主要参与交互的风电场定义为振荡源。

2.2 风电场振荡源定位的深度学习模型

传统的模式分析法是根据电力系统线性化模型状态矩阵的特征根及参与因子判断振荡源，具体步骤为：①建立如式（10）所示的电力系统线性化状态空间模型；②当振荡发生时，根据式（10）状态矩阵As可以计算出此时系统所有闭环模式ˆsλ及相应的参与因子PFsk；③根据振荡模式ˆskλ及其对应的参与因子，确定参与交互的风电场。根据2.1 节的分析可知，当风电场系统模式与剩余子系统中VSCHVDC 系统对应的模式接近时，可能发生谐振现象，体现在参与因子上为闭环振荡模式ˆskλ对应模式有风电场系统及VSC-HVDC 的参与因子两部分交互。因此，通过计算参与因子能够确认振荡源是哪个风电场和VSC-HVDC 系统。采用模式分析法确定振荡源的计算步骤为

式中，→表示计算顺序关系流向；j,i为振荡模式λsk对应的参与因子编号；PFsk为系统闭环模式ˆskλ的参与因子，表示受第s个状态变量激励的第k个模式在该状态变量时域响应中的参与程度，定义为

式中，wkT和vk分别为特征值λsk对应的左、右特征向量。

然而，建立线性化状态方程需要获知全部系统元件参数（运行参数和实际参数），这在实际系统中很难实现，且建立线性化模型的过程耗时较大，难以在线建模实现振荡源定位的应用。因此，为了能够实现离线建模并在线应用，提出数据驱动的替代方法。

在图3 系统中，风电场与VSC-HVDC 之间的汇集母线是风电场与外部系统进行能量交换的端口，而由图4 的全系统闭环互联模型可知，ΔVw与ΔYw作为输入、输出变量能够表征系统的整个状态，且变量均能够测量。由文献[16]，将ΔVw与ΔYw记为运行量测量Pw，则当系统结构确定时，不同运行条件下的运行量测量对应不同的系统状态矩阵As，即式（11）所包含的振荡模式或参与因子信息均包含在运行量测量中。根据式（11）的计算步骤及振荡源的定义，振荡源与参与因子及量测量之间的关系为

式中，S为风电场编号，S={0,1,…,M-1}，M表示风电场个数；g(·)为振荡源与参与因子的关系函数；f(·)为输入量Pw和输出量PF的函数。

综上所述，理论上如果能够获得系统所有运行条件下的运行量测量Pw，则系统的状态矩阵可近似确定，式（13）的关系也可近似拟合。然而，从实际系统获得所有运行条件下的运行量测量是不现实的，但可以确定的是由系统状态矩阵As得到的振荡源标签与量测量Pw存在如式（13）所示的确定关系，则可以通过离线仿真系统获得大量量测样本及振荡源标签，即式（13）的关系建模可以扩展到深度学习问题。其中函数g(f(·))即振荡源定位的模型。该模型没有精确解，根据深度学习方法，通过获取运行量测变量作为输入变量与振荡源真实标签作为输出变量的样本，训练对抗式迁移网络GDANN，训练好的网络可近似拟合振荡源定位模型记为

式中，Pw-real为实际运行量测数据。

该网络反映了运行量测数据与振荡源标签的映射关系。该网络在实际系统中通过给定真实量测数据，输出预测振荡源标签完成在线应用。

3 风电场经VSC-HVDC 并网系统振荡源定位实施方案

根据对抗式迁移学习的原理，以及风电场经VSC-HVDC 并网系统的振荡源定位模型，采用离线学习与在线应用相结合的方法，实现该系统的振荡源定位。具体实施方案分为系统构建与数据样本获取、离线模型训练和在线应用测试三个部分。

3.1 仿真系统等效建模与数据样本获取

实际系统中，风电场中风机数量庞大，复杂的动态特性与风机间的耦合关系使得式（6）所示的风电场状态空间模型阶数较高，仿真实施困难，因此，仿真系统通常采用恰当的假设或降阶模型，对风电场系统进行等效处理。基于电力系统等值理论[23]，针对并联结构的风电场，其子系统特征矩阵可通过选取参考风机及风电场线路拓扑结构信息进行估计。

在仿真系统中，根据开环模式谐振理论，模拟风电场次同步振荡的情况（本文主要考虑风电场中风机与VSC-HVDC 交互或风电场内部风机交互的情况）并进行时域仿真，设置仿真的采样频率为2kHz，仿真时长为2s。在进行时域仿真时，0.1s 时在系统并网节点随机施加85%～125%的功率扰动。设置各机组的额定功率按照同比增加或减少0～30%，负荷按初始值的80%～120%设置，从而更好地模拟实际系统的运行点范围，且比其运行范围更宽。记录每个风电场并网端口的样本数据集[Pw1,Qw1,Vw1,Vwθ1,…,Pwm,Qwm,Vwm,Vwθm]，系统的主导模式Yd=[λw1,…,λwM]，以及系统参与因子Ypf=[pw1,…,pwM]，并根据Yd、Ypf对每一个样本标注，形成测试系统的真实标签集Y。根据1.2 节的对抗式迁移学习原理可知，模型训练样本来源于仿真系统以及实际系统的少部分，因此，同上述过程，取实际系统中历史数据样本Xt，根据已知的振荡风电场，标注样本构造真实标签集Yt，形成目标域训练样本Dt。

3.2 风电场振荡源定位模型离线训练

3.2.1 网络搭建与参数设置

按照1.2 节提出模型搭建对抗式迁移网络，其网络参数设置主要包括三个子网络的输入输出层，卷积、池化层个数，卷积核、池化核相关参数。由于电力系统样本为振荡曲线，目标任务并不复杂，其特征不需要太过精细，因此，对原DANN 结构进行了适当缩减，并且在分类器网络只采用单隐藏层结构。本文采用的网络结构参数见表1。

表1 对抗式迁移学习网络参数设置Tab.1 Configuration of DANN

此外，进行模型训练还需要设置网络的学习率、激活函数、优化器和批次大小等。本文采用的网络训练超参数设置见表2。

表2 对抗式迁移学习网络训练参数设置Tab.2 Configuration of DANN training

3.2.2 模型评价与迭代更新

本文定义定位准确率指标LAI 来评价训练模型以及测试结果的精度。

式中，TN0为真预测为稳定的样本数目；TN1为风电场1 真预测为振荡源的样本数； 类似地，TNn为风电场n为振荡源的真预测样本数；Ns为参与评价样本总数。式（15）表示分类正确样本数占参与评价样本总数的百分比，表征训练模型的定位精度指标。

在模型训练时，通过留出法[24]对模型进行评估，即将数据样本（训练样本）划分为训练集与验证集。然后采用训练集进行训练（用训练集计算网络损失），并按照式（15）计算验证集精度。如果随着训练次数增加，验证集的精度能不断提高且最终稳定在较高精度，则说明得到了较好的稳定模型。本文中训练样本的定位精度都是验证集的精度。

对于每次训练，按照损失函数随机梯度下降方式迭代，更新网络参数，损失函数的计算在1.2 节中已做介绍，这里不再赘述。直到达到训练次数或训练集与验证集的定位精度均达到设定的阈值，停止训练，保存模型（本文为了设置对照实验，只设置了训练次数上限）。

3.3 振荡源定位的在线应用流程

在实际系统中获取量测数据，并按照网络输入规范输入数据，通过保存的离线模型输出定位结果。在进行一次计算输出后即完成一次，直到达到设定次数，停止输出。

综合以上次同步振荡源定位模型及实施流程，本文提出的方法的具体流程可分为三步：

1）针对实际系统案例基于系统等值理论构建仿真系统，并根据时域仿真及实际系统量测构造训练样本。

2）采用文中提供的对抗式迁移学习网络对训练样本进行学习，直至达到设定的阈值，停止并保存网络，此时的网络即为次同步振荡源定位模型。

3）将保存的模型应用于振荡源在线定位分析，当给定即时输入量测数据时，输出为振荡源标签。

因此，对于实际的多风电场经VSC-HVDC 并网系统的次同步振荡源定位问题均可采用以上方法流程进行振荡源定位模型的建模与应用。基于DANN的次同步振荡源定位流程如图5 所示。

图5 基于DANN 的次同步振荡源定位流程Fig.5 Scheme of SSO source locating based on DANN

4 算例

4.1 多风电场经VSC-HVDC 并网电力系统

在 Matlab 2019a 平台上搭建风电场经 VSCHVDC 并网的仿真系统用以模拟实际系统，其系统结构如图6 所示。其中两个风电场各包含10 台同型的风机，不同风电场的风机不同型，通过母线PCC汇集经过VSC-HVDC 系统接入交流主网（本文采用三机九节点系统代替交流主网）。根据前述的理论分析可知，风电场内风机可能与VSC-HVDC 系统发生动态交互，而本文设计的方法目的是定位参与交互的风电场。

图6 风电场经VSC-HVDC 并网系统Fig.6 Wind farms connected to the power system via VSC-HVDC

本文采用上述仿真系统模拟实际系统。为了模拟风电场与VSC-HVDC 发生次同步振荡，首先基于开环模式谐振理论调整系统两个风电场中风机及VSC-HVDC 的参数，设置风机与VSC-HVDC 发生次同步振荡的场景，并设置两个风电场分别是振荡源，详细参数设置见附表1。设置风电场1 与风电场2 及同步发电机总有功出力不变，而各机组的额定功率按照同比增加或减少0～20%，并网节点处负荷按初始值的90%～110%设置，得到若干运行点来模拟实际系统运行情况。

附表1 测试系统参数设置App.Tab.1 Parameter configuration of simulation system

图6 所示系统有两个作用：一是模拟实际系统产生测试样本；二是模拟实际系统产生少量目标域训练样本。根据系统任务，按照以下规则进行时域仿真，获得测试集与目标域训练集：

1）测试集：为了测试训练模型在此系统中定位次同步振荡源的准确性，采集不同运行条件下的样本进行测试。在风机与同步机发生交互场景下，任取一组发生次同步振荡的参数，随机在系统运行点下进行时域仿真，设置仿真的采样频率为2kHz，仿真时长为2s。暂态仿真时，在0.1s 时在系统并网节点施加85%的功率扰动。记录每一个运行点状态下，图中两个风电场并网线路上的有功功率P、无功功率Q以及节点d1与d2的电压幅值V、电压相角Vθ，形成样本数据集[Pw1,Qw1,Vw1,Vwθ1,Pw2,Qw2,Vw2,Vwθ2]，记录该运行点下系统的主导模式Yd=[λw1,λw2]，以及系统参与因子Ypf=[pw1,pw2]。重复上述仿真流程，生成200 个有效样本，剔除潮流不收敛的无效样本并对所有获取的电气量进行去均值处理及插值处理，形成测试集Dtest1={Xtest,Ytest}，其中Ytest表示根据系统的关键特征值与参与因子标注每一个测试样本，形成测试系统的真实标签集。

2）目标域训练集：同测试集的仿真流程，在风机与VSC-HVDC 交互的参数设置下进行时域仿真，并记录数据与系统主导模式及参与因子，生成500个有效样本，并构造测试集Dt={Xt,Yt}。需要注意的是在风机与VSC-HVDC 交互的参数设置下，由于运行点的变化也会存在稳态情况。

4.2 模型训练与测试结果

根据3.3 节提出的次同步振荡源定位方法的实施流程，针对图6 的实际系统，基于系统等值理论搭建仿真训练系统，得到仿真训练系统如图7 所示。

图7 风电场经VSC-HVDC 并网等效系统Fig.7 Equivalent system of wind farms connected with VSC-HVDC

在图7 所示仿真训练系统中，按照3.3 节中的流程，进行时域仿真，获得源域样本Ds。附录中以一个样本的形成为例，介绍了其仿真方法。将获得的源域样本与目标域训练样本统一形成训练样本，获得训练样本3 811 个，其训练样本主导特征根如图8 所示。

图8 训练样本主导特征根分布Fig.8 Distribution of eigenvalues of training samples

采用Facebook 公司发布的Pytorch1.2.0 框架搭建学习网络，并构建迁移学习的振荡源定位模型算法。计算机配置为Intel Xeon Gold-5217 (x2) 处理器，128G 内存， 搭配两片NVIDIA Tesla V100-16G GPU。采用图2 的网络对获得的样本进行训练。给出训练样本经过DANN 网络训练前后的对比如图9所示，采用t-SNE 对样本进行降维显示。

图9 训练样本经DANN 网络训练前后对比Fig.9 Comparison of training samples before and after DANN training

由图9 可知，训练前训练样本源域与目标域距离较大，训练后的数据样本更加接近，且有部分数据重合，说明DANN 通过学习提取两个域的公共特征，其域适应能力有效。进而，给出损失函数与训练精度的曲线如图10 所示。

图10 模型训练过程Fig.10 Model training process

由图10 可知，总损失函数呈下降趋势，说明网络收敛效果好，源域很快就可达到很高的定位精度，再增加训练次数，精度指标变化不大；目标域的训练集上精度波动较大，但其损失函数一直平稳下降，说明模型在不断对抗学习其公共特征。在训练到1 500 次左右，BatchSize 累计达到一半时，模型在两个域均达到很高的精度，并趋于稳定，可以用于模型迁移测试。

为了验证该模型的泛化性，本文给出不同域的训练样本的测试集精确度，与目标域测试样本进行对比。由于对抗学习在学习过程中通过博弈保存最优模型，为了对比不同模型的泛化性，分别对训练1 000 次与2 000 次保存最好的模型进行测试，结果见表3。

表3 模型测试结果Tab.3 Results of the trained model

由表3 的结果可知，训练1 000 次保存的模型虽然在源域具有很高的定位精度，但在目标域中的表现却不尽人意。而继续训练至2 000 次，源域定位精度保持不变，目标域定位精度不断提升，说明对抗网络不断学习来缩小两个域差异。由此可知，训练域样本达到较高的精度时，并不代表目标域也能有良好的表现，需要两个域均达到较高精度时，模型才会有较好的泛化性。从最终的目标域测试样本的测试结果可知，最后定位精度可达到100%，说明两个系统具有明显的公共特征，且振荡源具有易于区分的特征。

5 不同深度学习方法的效果对比

5.1 与传统卷积神经网络模型对比

卷积神经网络具有较强的特征提取能力，被广泛应用于深度学习中。为了对比验证本文所提方法的有效性以及对差异较大系统的泛化能力，采用传统卷积网络对源域训练样本进行学习，得到基于CNN 网络的振荡源定位模型，采用的网络结构见附图3。

在训练样本测试集与目标域测试集上分别对CNN 模型进行了测试，由于模型在1 000 次以后会严重过拟合，因此选择训练500 次与1 000 次的模型进行测试，其测试结果见表4。

由表4 的结果可知，传统CNN 模型在源域测试集能快速达到较高的精度，但在目标域的表现较差，模型呈现泛化性严重不足。并且在模型训练过程中，为了防止过拟合，通过增加正则的方式来缓解，但从测试结果看，是否加正则对模型泛化性的影响不大，这说明当系统差异较大时，该模型难以在实际系统中获得应用。

表4 传统CNN 模型测试结果Tab.4 Test results of the traditional CNN model

5.2 与传统模型迁移学习方法对比

传统的迁移方法以模型迁移居多，模型迁移又称为基于参数的迁移学习，该方法认为相似的任务之间会共享一些参数或者先验的超参数分布，将源域数据训练得到的网络参数直接移植入目标任务网络，并根据需要在已移植参数的网络后增加一个相对简单的网络，进而通过参数微调方法在此基础上进行微调，能够很快稳定训练出适合完成目标域任务的模型。因此，本文采用VGG16 网络进行迁移，通过冻结前4 层（共13 层），并在卷积层后增加全连接层与Softmax 分类层构成迁移网络。在该网络下，对源域样本只进行全连接层与分类器的训练，得到基于模型迁移的振荡源定位模型，采用的网络结构见附图4。

在训练样本测试集与目标域测试集上分别对该模型进行了测试，其测试结果见表5。

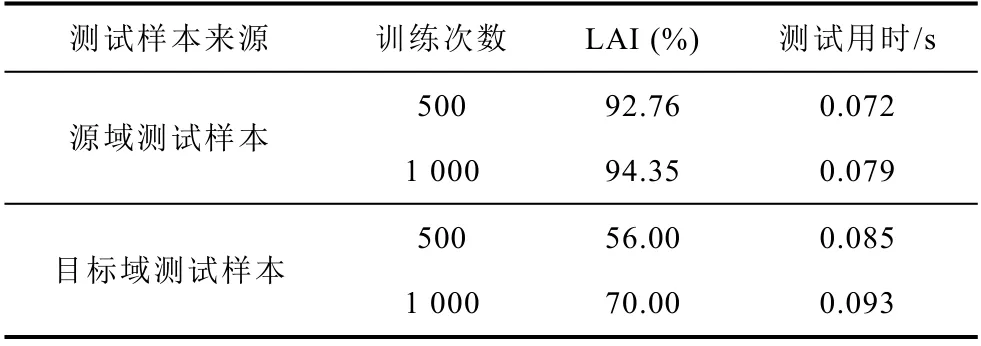
表5 传统的模型迁移学习方法测试结果Tab.5 Test results of the model transfer learning

由表5 的结果可知，与传统的CNN 学习方法类似，采用模型迁移的方法能够在源域测试样本获得较为精确的定位效果，但在目标域中的表现不佳，同样难以在实际系统中获得推广应用。该方法的优势在于训练速度可以得到快速提升，但从测试用时来看没有明显提升，而对于实际系统，并不需要在线建模。因此，模型迁移的方法在振荡源定位问题中适用性不强。

6 结论

本文基于对抗式迁移学习方法提出了多风电场经VSC-HVDC 并网的次同步振荡源定位的方法，并给出了该方法在实际应用时的具体实施流程。该方法通过对仿真系统与实际系统的样本进行对抗学习，从而缩小仿真系统与实际系统的域差异。通过设计多风电场经VSC-HVDC 并网系统案例验证了本文所提方法具有较高的定位精度。相比于传统的基于Prony、能量函数法等数值算法，本文所提供的方法不需要在线建模且定位速度快，更利于实现在线应用；而相比于其他深度学习算法，该方法基于特征迁移原理，具有更强的特征提取能力，对实际系统具有更强的泛化性。

综上所述，本文基于对抗式迁移学习网络，将深度学习在电力系统振荡稳定评估上的应用进一步发展，对未来实现大规模风电场振荡源在线定位有重要意义。智能电网的发展需要与计算机技术充分融合，而深度学习在其他领域的成功案例为在智能电网中的应用提供了良好的借鉴，充分考虑其差异性并发展强人工智能是未来实现电网智能化的目标。

附 录

1. 算例系统参数设置

（续）

2. 仿真样本的产生方法（以一个样本为例）

1）如3.2 节提供的仿真流程所述，根据开环模式谐振理论，在搭建的图7 所示线性化仿真系统中，调整参数使系统发生次同步振荡，参数设置为：风电场1 的d 轴外环比例积分系数为Kpd=0.8(pu)，Kpi=1 000(pu)；风电场2 的d 轴外环比例积分系数为Kpd=3(pu)，Kpi=100(pu)，风电场1 的出力为P1=1.2(pu)，风电场2 的出力为P2=1.5(pu)，并网节点上负荷无功功率为QL=0.05(pu)。此时，系统振荡模式为：0.31+j92.53，对应的参与因子如附图1 所示，则此时样本标注为1 号风电场是振荡源。

附图1 振荡模式对应参与因子App.Fig.1 Participation factor corresponding to the oscillation mode

2）进行时域仿真，在0.1s 设置扰动为额定功率的90%，并在0.2s 时切除。记录各风电场并网节点处的量测量，其波形图如附图2 所示。

附图2 仿真样本示意图App.Fig.2 Schematic diagram of a simulation sample

3. 测试所用网络结构

传统CNN 网络架构如附图3 所示。

附图3 传统CNN 网络结构App.Fig.3 Structure of traditional CNN network

模型迁移网络架构如附图4 所示。

附图4 基于VGG16 的模型迁移网络结构App.Fig.4 Structure of transfer network based on VGG16 model