轴系结构方案正向设计数字化方法研究

郭宇名，邱 俊，王德伦

(大连理工大学机械工程学院, 辽宁 大连 116024)

轴系一般由轴、轴承以及传动构件组成，是传动系统中重要的组件，其主要功能是传递运动和转矩。几乎所有的机械系统都有轴系，例如齿轮箱各传动轴、机床主轴、风电传动轴系等。轴系结构方案的设计决定着轴系的性能，如寿命、强度、经济性等。

传统的轴系结构方案设计的基本方法是采用可行方案校核迭代的方式进行轴系结构方案设计[1-3]，但是生成的可行方案仅仅停留在性能满足要求上，对体积、质量等参数无法做到控制和优化。随着计算机技术的发展，计算机辅助设计轴系结构成为重要的研究领域，且因为计算机的运算能力使得轴系结构方案的优化成为了可能。文献[4]以体积最小为优化目标优化了高速轴系主轴的结构参数；文献[5]以飞轮质量最小为目标优化了飞轮储能系统轴系。然而以上两种优化方法均未考虑轴承的尺寸和性能，具有一定的局限性。计算机辅助设计的另一个巨大优势就是图形变换和实体造型技术，能以更高的效率输出工程图和三维模型[6-7]，但是上面提到的计算机辅助设计方法仅能实现简单的选型和校核运算，无法对轴系结构进行从无到有的设计。

综上，传统的轴系设计只能满足性能要求和尺寸约束，无法优化结构参数。引入计算机辅助设计技术后可以得到更优的参数，进行更快捷的表达，但是可优化的参数太少，设计流程也并非从无到有。本文提出的正向设计数字化方法实现了轴系结构从无到有的正向设计，且优化时考虑了轴和轴承的总体尺寸和性能，运用该方法可以生成多种不同的轴系结构方案供用户选择。

1 轴系布局设计

从力学模型的角度出发，轴系可以简化为轴、支撑点、载荷点的组合，轴系布局设计的实质是支撑点、载荷点相对位置关系的确定。

载荷点为轴系承载外载荷的受力点，支撑点为轴系支撑对轴承产生支反力的作用点。轴系布局设计即在给定载荷点和支撑点的前提下将载荷点和支撑点进行排列组合，得到多种不同的轴系布局方案，每种方案对应着不同的力学模型。设该轴系有n个载荷点、m个支撑点，载荷点是互不相同的，要区分顺序，支撑点不区分顺序，基于此得到轴系布局的方案数Pmn的计算公式如下：

(1)

式中：A是数学中的排列数。

当n=2、m=2时，轴系布局方案共有6种，其示意图如图1所示。

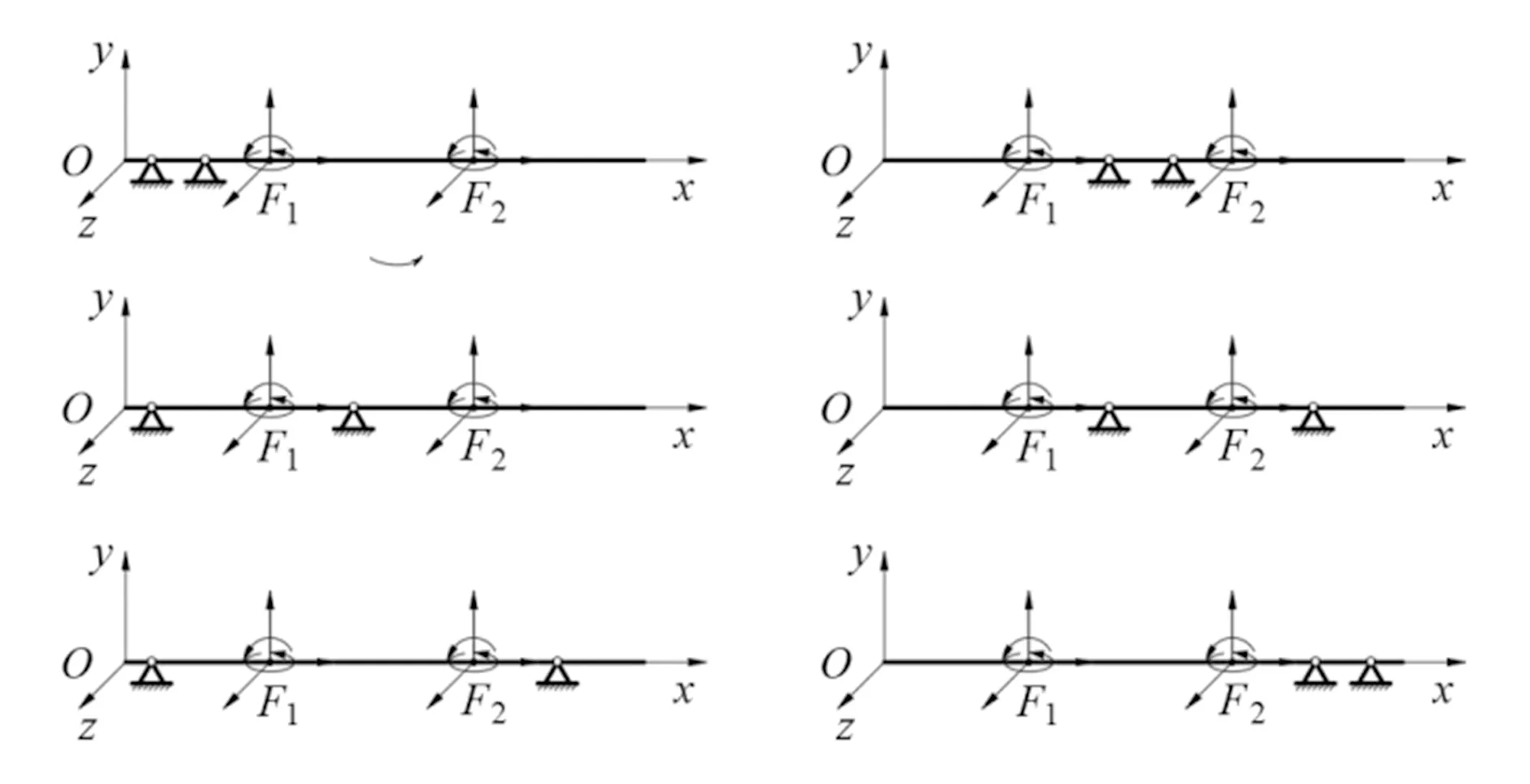
图1 n=2、m=2时轴系布局方案示意图

2 支点结构化设计

2.1 轴系约束与定位

轴系坐标系以轴端面与轴向中心线的交点为原点，轴向中心线为x轴，轴的两个径向分量分别为y轴和z轴，如图2所示。

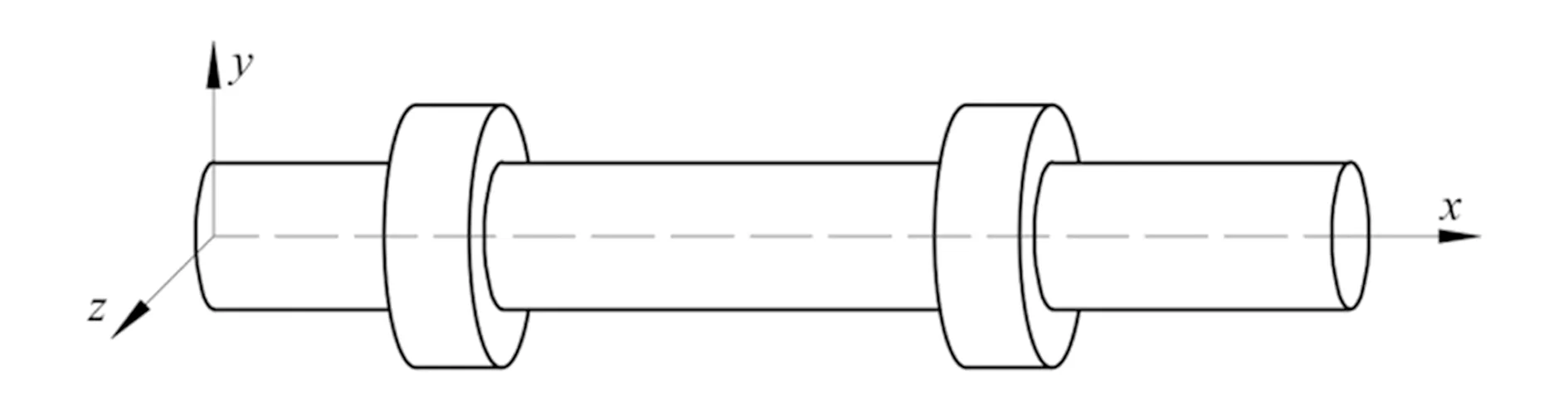
图2 轴系定位坐标系示意图

在此引入约束向量A来表达几何约束形式限制的自由度信息[8]：

A=[x,y,z,Rx,Ry,Rz]T

(2)

式中：x,y,z为移动自由度；Rx,Ry,Rz为转动自由度。式中元素取0时表示未限制自由度，取+1表示正向自由度被限制，取-1表示负向自由度被限制；取1表示正向或负向的单向自由度被限制，取±1表示双向自由度均被限制。

向心轴承i(i=1,2)对轴的约束向量Ab1，Ab2可表示为：

Abi=[xbi,±1,±1,0,0,0]Ti=1,2

(3)

式中：xbi为轴承i在x轴上对轴的约束，会根据轴承结构的不同而变化。当两个轴承共同支撑一个轴时，其约束向量的组合结果即为轴的约束向量，且轴在轴系中只有确定的回转运动。设轴上其他零件对轴的约束向量为Ac，轴的总约束向量为As，可得如下约束向量方程：

As=Ab1∪Ab2∪Ac=[±1,±1,±1,0,

±1,±1]T

(4)

轴沿y和z方向的双向转动约束可以由两个以上向心轴承的组合提供，轴在x方向的移动约束包括轴承的移动约束和轴上其他零件的移动约束。根据回转副的矩阵分解原则，轴在x方向移动自由度的分解结果为：

(5)

这3种分解结果分别对应轴承的3种配置方式：双支点单向固定、单支点双向固定、两端游动。

2.2 工况驱动结构设计

轴系的工况即为轴系的运行状态，包括转速和载荷，这些状态会影响方案选择的合理性。程序应根据工况对支点结构化进行定性排序，避免用户在选择方案时被过多的非常用方案分散精力。在此给出一般性的排序原则：

1)转速高(大于10 000 r/min)时应优先使用球轴承，转速低(小于10 000 r/min)时应优先使用滚子轴承。

2)当轴系载荷为纯径向力时优先使用径向接触轴承，当轴系载荷存在轴向力时优先使用成对角接触向心轴承方案，也可选用单支点双向固定的方案。

经过筛选得到多组轴承组合类型和轴承配置方式，然后进行轴承型号的初选。初选轴承时需要计算轴的最小直径，以确定轴承的内径。由于轴的结构未知，因此需根据轴的材料、转速和功率求出轴的最小直径dmin，最小直径计算公式为：

(6)

式中：P为轴的功率，kW；n为轴的转速，r/min；A0为轴的材料系数。A0的计算公式如下：

(7)

式中：[τr]为材料的许用扭转切应力。

得到最小轴径后可以确定轴承内径，初选轴承型号，然后进行校核，若校核成功，则得到该轴系的轴承型号，若不成功，则在该内径下选用更大尺寸的轴承，直至轴承校核成功为止。

3 轴系力学模型与数字模型

3.1 轴系力学模型

力学模型用于求解轴上各受力点所受的力。力学模型求解包括轴承支反力(轴承所受径向力)求解和轴承所受轴向力求解。

轴承支反力求解只需根据受力平衡方程计算即可，因此对于所有轴承而言计算支反力的方法是一样的。在此以载荷点数为2、支撑点数为2的情况为例，建立轴系力学模型简图如图3所示。

图3 轴系力学模型简图

图中Fx,Fy,Fz分别为各点x,y,z方向的作用力，Mx,My,Mz分别为各点绕x轴、y轴、z轴的力矩。将轴上最外侧的受力点设置为原点，将所有的受力均假设为集中力，正方向均为坐标轴正方向，下标x1,x2,x3,…为受力点的坐标，可得6个方向的受力平衡方程为：

(8)

式中：MyFi和MzFi分别为轴上第i个受力点沿y和z方向的作用力在原点处产生的力矩，计算公式为：

(9)

由此可解得轴承在xy平面的支反力：

(10)

相比于xy平面，xz平面的力矩正方向为顺时针方向，同理解得xz平面支反力：

(11)

式(10)和式(11)由式(8)的受力平衡方程求解得出，当轴承点(此处等价于支撑点，安装轴承的点)所属的受力点序号或载荷点数量发生变化时可同理得到相同形式的结果，因此其他情况的通式本文不作赘述。

假如使用的轴承包含角接触向心轴承，则在计算完轴承所受的径向力后还需计算轴承所受的轴向力，轴承所受的轴向力计算方法取决于轴承的配置方式和轴承型号，计算方法见国家标准，本文不做赘述。

3.2 轴系数字模型

为了运用计算机进行轴系结构方案的自动设计，需要建立计算机可识别的轴系方案数字模型。轴系方案数字模型包括布局数字模型、力学数字模型和结构数字模型。

布局数字模型即轴系布局的数字化表示方法，根据第1章的轴系布局受力点类型和受力点相对位置关系，定义布局向量S：

S=[s1,s2,…,sp]

(12)

式中：p为受力点的总数量；si为轴上第i个受力点的类型。在此将滚动轴承用B表示，齿轮用G表示，如轴上零件的安装序列为典型的“滚动轴承—齿轮—齿轮—滚动轴承”序列，则轴的构型向量为[B,G,G,B]。需要注意的是该序列基于图2坐标系中的x轴正方向定义，且根据x轴正方向进行顺序编号，即轴承1—齿轮1—齿轮2—轴承2。

力学数字模型表征轴系上受力点信息，配合布局数字模型可完全确定轴系各受力点的属性(载荷点或支撑点)、位置和大小。力的3个要素分别为大小、方向和作用点，力的大小和方向可以用3个坐标轴方向的分力和分力矩的大小来表示，作用点则用受力点在x轴上的坐标来表示。在此定义轴的受力矩阵F和载荷点坐标矩阵XF：受力矩阵的各列对应各载荷点的受力信息共6行，表征该点6个维度的受力；载荷点坐标矩阵为行向量，各列对应各载荷点的位置信息。

结构数字模型表征轴系各部分结构参数，包括轴系各零件的结构参数和装配参数。零件结构参数即表征零件尺寸的参数；装配参数为表征轴上零件相对位置尺寸的参数。

4 轴系尺寸参数设计

4.1 目标函数

对于实际工程而言，轴系的设计应保证结构紧凑，占用空间小，因此本文的优化目标为轴系的体积V最小。轴系体积包括两个部分：轴承的体积Vb和轴的体积Vs，计算公式如下：

(13)

式中：Tbi,Rbi,rbi分别为第i个轴承的副高(轴承的最厚尺寸)、外圈半径和内圈半径；ns为轴段总数；li为第i个轴段的长度；dsi为第i个轴段的直径。

4.2 优化变量

优化变量为除轴承轴段外的其他轴段轴径，所有载荷点位置和所有轴承型号，对于不同数量的轴承点和载荷点的方案，优化变量数量不同。在此以轴承1—齿轮1—齿轮2—轴承2的典型布局序列为例，优化变量组成的向量X可表示为：

X=[x2,x3,x4,d2,d3,d4,c1,c2]

(14)

式中：x2，x3，x4分别为第2,3,4个受力点的位置；d2,d3,d4分别为第2,3,4个轴段的直径；c1，c2为轴承的型号。因为根据图3所示的坐标系，x1的值恒为0，所以x1不是优化变量。又因d1和d5为轴与轴承配合的轴段直径，与轴承型号关联，所以d1和d5也不是优化变量。

4.3 约束函数

轴承基本额定寿命均大于等于整个轴系需求的基本额定寿命：

min{L10i|i=1,2,…,m}≥[L10]

(15)

式中：L10i为第i个轴承的额定寿命；[L10]为用户设定的整个轴系需求的基本额定寿命；轴承额定寿命计算公式[9]为：

(16)

式中：C为轴承的额定动载荷，由轴承型号决定；Ps为当量动载荷；ε为寿命指数，球轴承ε=3，滚子轴承ε=10/3。

轴的轴肩过渡应满足如下要求：轴承定位轴肩所在轴段直径应满足轴承定位直径约束；定位轴肩高度应大于较小轴径固定倍数的值；过渡轴肩高度应大于轴肩的过渡圆角半径的2倍。现列出通用公式：

(17)

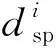
轴上的零件实体不能发生干涉，各零件的间距应大于等于用户设定的最小间距，如下式：

xBi-xBi-1≥0.5(Bi+Bi-1)+gmin

(18)

式中：xBi为轴上第i个受力点对应的零件宽度中心在力学模型坐标系中的坐标；Bi为轴上第i个受力点对应的零件宽度，对于轴承则是副高；gmin为轴上零件的最小间距。

轴的疲劳强度应满足要求：

(19)

式中：Ss为轴的疲劳强度安全系数；Sσ为轴的弯曲疲劳强度安全系数；Sτ为轴的扭转疲劳强度安全系数；SP为轴的许用疲劳强度安全系数。

式(19)是针对危险截面的，根据弯矩和剪力的微分关系可知轴上的受力点是弯矩的极大值点，所以危险截面的位置为各受力点的位置。当所有危险截面均校核通过时轴的疲劳强度满足要求。

轴系长度La应控制在一定范围内。轴系长度为轴系最外侧两个零件的外端面之间的距离，在此引入轴系长度允许变动量，即设计出的轴系的长度相较于最紧凑结构(轴上所有零件的间距为最小间距)下轴系长度的差值，用δ表示，该约束的表达式为：

(20)

4.4 算法与初始值

本文所提出的优化模型为单目标优化模型，且目标函数为非线性函数，约束函数也为非线性函数，故使用序列二次规划法(SQP)对其进行求解。

载荷点位置初始值可依据零件间均相隔最小间距来计算确定，轴径初值可根据式(17)中约束的下边界来确定。

5 算例分析

设某二级齿轮箱减速器功率为3.4 kW，三根轴沿同一水平线平行放置，两对齿轮均已设计完毕，现需要设计中间轴轴系的结构方案。已知中间轴转速为114.56 r/min，中间轴上齿轮参数见表1。

表1 齿轮参数表

经计算，该轴系的扭矩为70.23 N·m，齿轮受力的计算公式如下：

(21)

式中：Ft为齿轮所受切向力；Fr为齿轮所受径向力；Fa为齿轮所受轴向力；T为轴系传递扭矩。

轴系坐标系及齿轮受力示意图如图4所示。

图4 轴系坐标系及齿轮受力示意图

经计算可得两个齿轮的受力，本例中两个齿轮即为两个载荷点。结合轴系坐标系方向，可以得到两个载荷点受力矩阵，见表2。

表2 齿轮受力表

本例中轴的材料为45钢，采用双点支撑，设计输入参数见表3。

表3 设计输入参数

因采用双点支撑，且有两个载荷点，所以轴系布局有6种，如图1所示。本文从中筛选出纯简支布局的方案进行设计和优化，由此可得该布局下的构型向量为[B,G,G,B]。

由表2可知，轴系在轴向受较大载荷，根据2.2中工况驱动结构设计的筛选规则，优先使用圆锥滚子轴承+圆锥滚子轴承或角接触球轴承+角接触球轴承等可以承受双向轴向载荷的轴承组合。该方案的轴系通用结构及各轴段编号如图5所示。

图5 轴系通用结构示意图

本例中的优化目标为轴系的体积，优化变量为除轴承轴段外的其他轴径、所有载荷点位置和所有

轴承型号。轴系的轴径约束如下：

(22)

式中：da max 1，da min 1分别为轴承1定位的最大和最小直径。

为了表示方便，单列圆锥滚子轴承、双列圆锥滚子轴承、圆柱滚子轴承分别用TRB，DTRB，CRB表示；双支点单向固定、单支点双向固定分别用编号1和2来表示。程序计算出的两个方案结果如表4～表6所示。表中所涉及的符号含义如图5所示。

表4 各方案轴结构设计结果表

表5 各方案轴承设计结果表

表6 各方案键设计结果表 单位：mm

注：bk1，bk2分别为键槽1，2的宽度；hk1，hk2分别为键槽1，2的深度；Lk1，Lk2分别为键槽1，2的长度。

两种方案的轴系结构示意图如图6所示。

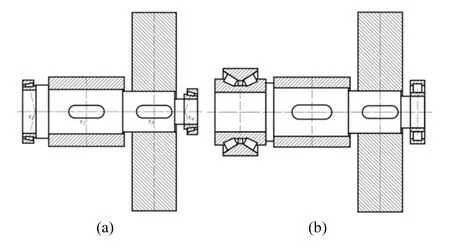
图6 设计结果结构示意图

6 结束语

本文实现了轴系结构方案的正向数字化设计。

以轴系布局设计、支点结构化设计和轴系尺寸参数设计为设计路线，研究了轴系从基本工况和性能条件到结构方案的自动化设计方法，并建立了轴系的力学模型、数字模型和优化模型，实现了计算机辅助的自动化设计。最后通过算例详细说明了从最初需求到形成方案的过程，并输出了其中两种方案的结果参数。