基于有限元仿真的齿轮滚切稳定性建模与分析
陶振雷,濮潇楠,田树飞,汤海川,郝继铭,王禹林
(1.南京理工大学机械工程学院,江苏 南京 210094)(2.重庆大学机械工程学院, 重庆 400044)(3.重庆蓝黛动力传动机械股份有限公司, 重庆 402760)
随着科学技术的发展,高速干切加工已成为最广泛、最先进的齿轮加工技术之一。在滚齿干切加工过程中,当系统结构参数或滚削参数选用不当时,刀具与工件之间会产生颤振,这已成为限制滚齿加工精度的重要约束[1]。颤振在齿轮表面留下的振纹,会降低齿面质量,影响产品的合格率。此外,颤振还会带来机床损伤、刀具磨损加速等不良影响[2]。
抑制或避免颤振的可行途径是确定滚齿加工参数,使其远离所预测的颤振发生临界条件[3-4]。稳定性叶瓣图分析法是颤振临界条件预测的主流方法之一,叶瓣图可以简单而清晰地描述刀具切深与刀具主轴转速的对应关系,通过加工参数落在叶瓣图上的位置预测加工系统的稳定性,因而在切削颤振分析中得到广泛应用[5]。
目前,稳定性叶瓣图分析法主要应用在切削深度恒定的车、铣削工艺中。邓聪颖等[5]针对机床运行状态切削稳定性的准确预测问题,提出一种切削稳定性叶瓣图研究方法,但建模参数需通过试验确定,试验方案繁琐。赵铁民等[6]针对铣削稳定性中经常出现的颤振现象进行了研究,分析了铣削颤振稳定域。夏玉等[7]通过滚齿切削力模型研究了滚齿颤振机理。陈鹏等[8]建立了一种齿轮高速干切工艺参数优化模型,基于工件材料属性和相关试验推算滚刀转速与切削厚度的推荐值。以上研究都没有解决叶瓣图建模参数获取问题。将叶瓣图运用于滚齿加工时存在以下两个难点:1)叶瓣图所需的动力学参数一般通过实验获取,但由于滚齿运动复杂,相关试验不易开展;2)滚齿运动由一系列展成运动构成,不是单纯的正交切削,而滚削过程中的切削方向随着刀刃切入切出而不断变化,其极限切厚不可控。本文将针对这两个问题展开研究。
本文针对叶瓣图应用于滚齿稳定性分析时动力学参数获取困难等问题,通过模态和切削力有限元仿真方法,获取滚刀系统的模态参数和动力学参数,建立滚齿稳定性叶瓣图。
1 滚齿叶瓣图理论模型
首先通过滚齿动力学模型建立滚齿加工系统的微分方程,推导建立滚齿稳定性叶瓣图模型所需关键参数,基于有限元模态和动力学仿真获取模态和动力学参数并绘制出叶瓣图,再通过经验公式建立滚齿进给量和切厚的函数关系,从而确定合理的工艺参数。
1.1 滚齿动力学模型
为方便研究,将滚齿系统简化为由滚刀和毛坯组成的振动模型,并建立振动模型的特征方程,利用特征方程求解维持系统稳定的加工参数。滚齿的二维平面动力学模型如图1所示。
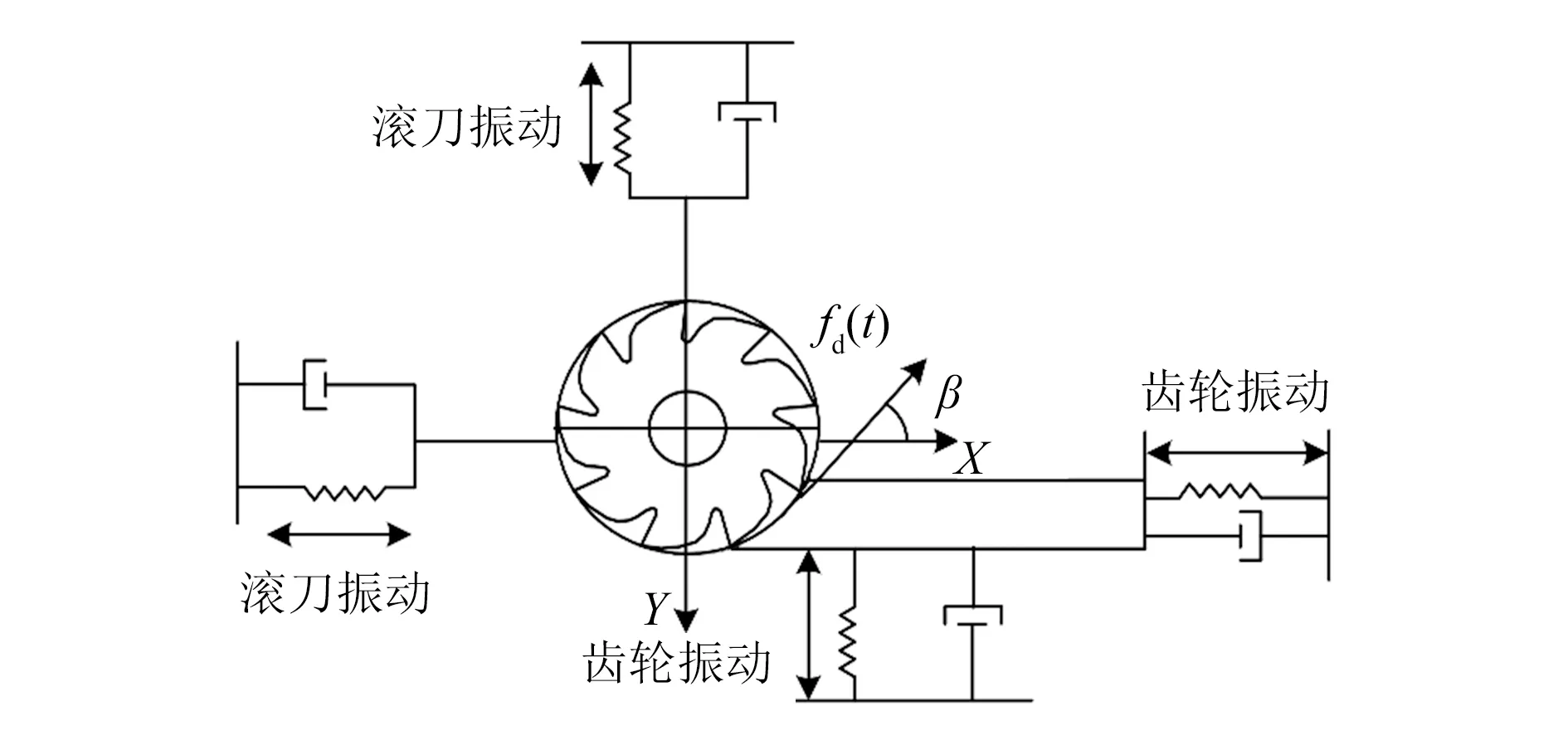
图1 滚齿的二维平面动力学模型
通过滚齿动力学模型建立的振动系统运动微分方程为[9]
(1)
式中:t为时间;x(t)为振动位移量;fd(t)为动态切削力;me为振动系统等效质量;c为振动系统等效阻尼系数;k为振动系统等效刚度;β为螺旋角。将切削力代入式(1)得
(2)
式中:kf为切削刚度系数;b为切削宽度;T为前后两转的延时时间。对式(2)进行拉普拉斯变换,得到其传递函数Γ(s)为
(3)
式中:ωn为无阻尼自然振荡频率;ξ为阻尼系数;s=σ+jω,且仅当实部σ=0时,系统处于临界状态,ω为系统的颤振频率。其极限切削宽度blim可以表示为
(4)
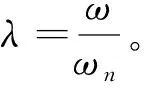

在其他参数都确定的情况下,可根据式(4)确定极限切削宽度blim与主轴转速n的关系,构建滚齿系统的稳定域极限,对于极限切削宽度blim,还未确定的参数有滚刀系统模态参数以及动力学参数。
1.2 滚齿加工参数确定
与车削、铣削加工相比,滚齿切削的运动方式更为复杂,其运动由两个方面组成,分别是滚刀与毛坯件之间的展成运动和滚刀沿坯件轴线方向的进给运动。因此,滚齿切削加工的切宽主要表现为滚齿展成运动过程中的滚刀顶刃最大切削厚度h1max。Fabre等[10]建立了滚刀顶刃切削厚度与工件每转的轴向进给量关系式。
本文研究的齿轮参数为法向模数1.7,齿数37,全齿高5.275 mm,齿轮外径79.15 mm。滚刀参数为外径70 mm,刃数10,头数3,中心距70 mm。由已知参数可以建立滚齿进给量fa与切削厚度h1max的函数关系,获得叶瓣图与滚齿加工参数的对应关系。
2 滚齿系统模态参数确定
2.1 滚刀系统模态仿真
为获得构建滚齿稳定性叶瓣图所需的系统模态参数,采用ABAQUS有限元分析软件对滚刀进行了有限元模态分析。滚刀材料为M35钢,其具有高硬度、高红硬性和高耐磨性等特点,宜用来制造强力切割用耐磨、耐冲击的工具。在分析步中将阶次设置为4阶。滚刀材料属性表见表1[11]。

表1 滚刀材料属性表
模态仿真结果图如图2所示,滚刀模态参数见表2。

图2 模态仿真结果

表2 滚刀模态参数
2.2 滚刀系统模态力锤试验
为验证滚刀模态分析的正确性,采用锤击法对滚齿机床滚刀系统进行模态力锤试验,以获得相应的模态参数。
通过力锤试验获得的滚刀系统前4阶固有频率及其对应的阻尼比见表2。通过模态仿真获得的滚齿系统固有频率参数与模态力锤试验获得的固有频率相近,从而为滚齿稳定性叶瓣图的建模提供了固有频率及阻尼比。
3 滚齿系统切削力系数确定
首先确定材料的相关参数,本文所采用的齿轮毛坯材料为20CrMnTi,查找相关文献[12]得到其性能参数,见表3,其中A,B,n,C,m为材料本构常数。

表3 20CrMnTi齿轮材料性能参数
本文采用Jonhson-Cook强度模型作为本构模型,采用Jonhson-Cook剪切失效准则作为刀屑分离的准则。20CrMnTi齿轮的失效参数D1~D5见表4。

表4 材料失效参数
滚刀以其螺旋升角安装在滚刀轴上,滚齿进给量fa采用0.5 mm/r,转速为450 r/min,持续时间选取1 s,进行滚削仿真。
在实际的加工中,切削力系数与切削参数、切削条件、刀具-工件材料组合有关,由其切削力及切削总量共同决定,通过滚削力仿真,得到滚削时间为0.2 s内的滚削力图,并通过布尔运算求得此期间的滚削总量为2.356 mm3,对滚削力每个波峰波谷所得出的切削力变化量进行加权平均并除以滚削量,得到kf=2.414×1011N/m3。至此已获得建立叶瓣图所需所有参数。
4 滚齿叶瓣图建模及加工试验
4.1 叶瓣图建模
颤振稳定性叶瓣图可以直观说明转速与切厚的关系,是颤振稳定性分析的常用方法。叶瓣图分为稳定切削域、不稳定切削域和条件稳定域。在实际加工中,稳定切削域越大,机床的稳定性能越好。
通过2和3中的仿真及试验获得模态参数和切削力系数,结合式(4),可绘制出滚齿加工稳定性叶瓣图,如图3所示。
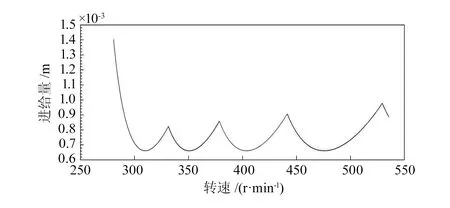
图3 滚齿加工稳定性叶瓣图
图中曲线下方为稳定切削域,上方为不稳定切削域,曲线附近为条件稳定域。波谷处的极限切厚为0.65~0.67 mm,下文将取各极限切厚下对应的转速进行滚齿试验,以验证叶瓣图的正确性。
4.2 滚齿加工试验
4.2.1试验系统及条件
在仅改变进给量和转速的情况下,若系统出现激烈振动且伴随强烈噪声,则认为系统处于不稳定状态,通过分析振动加速度传感器采集的振动信号来判断是否发生颤振,并将转换得出的最大切削厚度h1max与所建立的叶瓣图模型取值进行对比,验证叶瓣图的正确性。试验参数设定见表5。

表5 试验参数设定值
将带磁座的振动加速度传感器安装于滚刀轴的X和Y进给方向上。传感器安装位置如图4所示。

图4 振动传感器安装位置
4.2.2试验分析
由于试验数据量大,受篇幅限制,本文仅以转速480 r/min为例进行试验数据分析,其他试验数据分析方法相类似,不再赘述。此转速下各进给量通过经验公式可转化为对应的最大切厚,分别为0.2,0.4,0.6 mm。空转及各切厚下振动信号幅值如图5所示。

图5 振动时域图
由图5可知,当滚刀顶刃最大切削厚度为0.2 mm时,振动幅值均在5 m/s2以下,当切削厚度增加到0.4 mm时,振动幅值略有增加,但仍在5 m/s2附近,当增加到0.6 mm时,振动幅值发生明显突增,突变处增加到7 m/s2,由此判断出当切削厚度为0.6 mm时滚齿系统处于不稳定状态。
分别对切削厚度为0.2 mm和0.6 mm时的振动信号进行傅里叶变换,得到频域下系统的振动幅值图如图6所示。
由图可知,在切削厚度为0.2 mm时,滚刀轴在800 Hz左右处振动幅值最大,为2.8 m/s2,当切削厚度增加到0.6 mm时,800 Hz处的振动幅值明显增大,为7 m/s2,并且振动频率与仿真所得的固有频率值接近,说明滚刀系统的颤振频率在800 Hz附近。
对3种进给量下加工出的齿轮产品进行质量检测,检测项目为齿形和齿向,检测结果见表6。
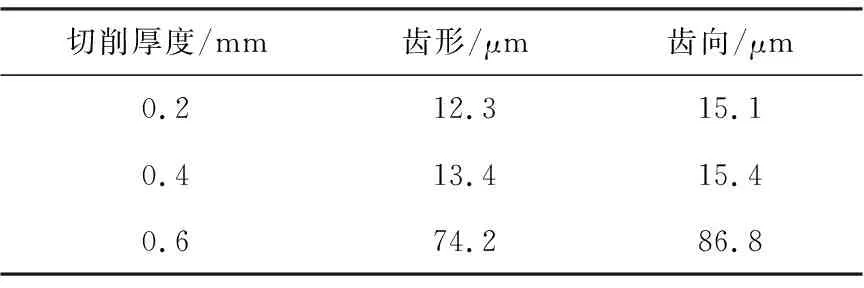
表6 加工试件齿形、齿向检测值
根据滚齿粗加工质量检测标准,当试件的齿形、齿向检测值在20 μm以下时,认为零件为合格产品。由表6可知,当切削厚度为0.2和0.4 mm时,被加工试件的齿形、齿向平均检测值均小于标准值,当切削厚度为0.6 mm时,齿形、齿向平均检测值远大于标准值,由此可知,此时滚齿系统处于不稳定状态,加工出的试件为不合格产品。
对比试验得到的极限切厚点与基于仿真方法绘制的稳定性叶瓣图中的相关数据点可知,图3所示的滚齿稳定性叶瓣图得出的波谷处的极限切厚值为0.66 mm,与试验所得的极限切厚0.6 mm相接近,说明通过仿真参数建立滚齿稳定性叶瓣图来分析滚齿加工稳定性具有可行性。
5 结束语
本文通过模态和滚齿有限元仿真分析获得模态和动力学参数,并建立滚齿稳定性叶瓣图模型。基于稳定性叶瓣图设计开展不同转速和进给量下的滚齿切削试验,并以480 r/min下的试验数据为例进行分析,所得极限切厚约为0.6 mm,略小于叶瓣图所示的极限切厚值0.66 mm,验证了通过仿真参数建立稳定性叶瓣图并分析滚齿加工稳定性的可行性。本文通过仿真方法解决了滚齿加工动力学参数获取困难的问题,可为滚齿工艺稳定性分析、切削参数选择提供参考。

