多种失效模式下高速公路复杂网络可靠性研究

王晚香，张佳垚，郭瑞军

(大连交通大学 交通运输工程学院，辽宁 大连 116028)

路网可靠性是道路交通网络达到某种服务水平的可靠程度[1]，对特定路网可靠性进行综合评价，对于道路管理者来说不仅有助于针对不同时段的交通流量对路网进行优化，提高路网整体的通达性，也能够在路网中出现事故或自然灾害而导致路网整体结构被破坏时提出合理可行的应急方案，减少道路使用者的行程时间，提高运输效率.

研究路网结构及运行的指标有抗毁性、可靠性和鲁棒性等，道路运输系统的抗毁性[2]是其对于交通事件的敏感程度，交通事件可导致道路网络服务能力的减少.1995年日本神户发生大地震以后，交通学者对交通网络可靠性进行了深入研究，特别是在出行时间可靠性方面有了许多研究成果[3].Sohn Keemin等[8]提出了估计路段行程时间动态变化的方法，为准确计算行程时间可靠性奠定了基础.Sumalee等[9]指出动态行程时间可靠性的关键是动态行程时间分布估计，设计了一种抽样过程估计路段行程时间的概率质量函数，分析了路段行程时间在随机和动态变化下的分布特征，并在此基础上计算了行程时间可靠性.孙健[10]利用VISSIM仿真软件研究了不同突发情况下区域路网的连通可靠性、行程时间可靠性和路网容量可靠性.方雅君等人[11]根据路段容量的约束建立了可靠性双层模型，利用灵敏度分析的方法比较不同路段服容量的路网性能.陈琨[12]等分别考虑路段相关和路段独立两种情况，建立了基于对数正态分布的路径行程时间可靠性评价模型.Higatani Akito等人[13]于2009年利用实地采集数据研究了Hanshin高速公路网络行程时间可靠性.郭志勇等[14]利用浮动车调查数据，在不同的时间段内计算出了路径的行程时间可靠性，并基于此建立了城市区域控制系统运营效率的评价模型.许良[15]选取了连通可靠性、出行时间可靠性和能力可靠性指标作为城市道路交通网络设计问题的优化目标，分别建立了相应的城市道路交通连续网络设计模型.柏喜红[16]总结了变异系数、缓冲时间、延迟行程及行程时间分布等行程时间可靠性指标.

实际的交通网络中不同道路的设计速度有很大不同.假如不同等级道路上的所有车辆速度统一计算其平均速度，可靠性计算则变得不可靠，因此，大部分路网可靠性模型只适用于单条道路，对于大规模路网则不适合.

本文通过对某区域高速公路网的对偶法拓扑结构建模，求出了拓扑网络的节点度，针对随机攻击和选择攻击，总结路网连通可靠性的变化规律，并提出了计算行程时间可靠性的新方法，研究在不同行程时间系数和延迟系数下，路网的行程时间可靠性的变化规律，在道路阻断与拥挤的混合条件下，计算了路网的可靠性.

1 公路复杂网络的可靠性相关参数

复杂网络的各项指标中本文仅介绍节点度和可靠性指标，其中可靠性又包含连通可靠性、行程时间可靠性以及路网可靠性三种可靠性指标.

1.1 节点度

设k(vi)代表节点度，表示与第i个节点连接的连线数量，公式为

(1)

式中：N为节点总数；dij表示节点vi与节点vj的连接情况，若连接取dij=1，反之取dij=0.

1.2 连通可靠性

连通可靠性为路网中任意两个节点之间至少存在一条路径连通的概率[13].对于整个路网只要任意两点间存在通路则认为该公路网在某种程度上是可靠的.其计算公式为：

(2)

式中：RC为网络连通可靠性，0≤RC≤1全连通网络时取值为1；ω为移除节点后所形成的子网数量；Ni为第i个子网所能贯通的节点数量；di为第i个子网的平均最短路径.

1.3 行程时间可靠性

1.3.1 路段行程时间

一般以BPR函数计算路段行程时间，具体形式如下：

(3)

式中：Ta为路段a上的行程时间；xa为路段a上的交通流量；Ca为路段a的通行能力；β、n参数需根据实际情况标定.

1.3.2 基于变异系数的行程时间可靠性

基于数理统计的方法是统计车辆的行程时间数据，将其变异系数作为行程时间可靠性[12]，其计算公式如下：

方差S(t)为：

(4)

标准差σ为：

(5)

变异系数CV(t)为：

(6)

1.3.3 基于延迟行程指标的行程时间可靠性

延迟行程指标利用行程遭遇指数来表示路网的不可靠性[17]，主要针对突发事件时高速公路的可靠性研究.计算公式为：

(7)

1.3.4 基于延迟系数的行程时间可靠性模型设计

考虑到变异系数、遭遇指数和BPR函数三种方法只能计算单条路段行车时间的局限性，本文设计基于延迟系数的行程时间可靠性模型如下：

以最大限速为v可得单位距离的行程时间，作为最小单位行程时间tmin.由每条高速公路的平均行程速度可以计算其单位行程时间，并求第i条(i=1,…,n,n为道路条数)高速公路的单位行程时间ti与最小单位行程时间的相对比值，称为行程时间系数，其均值Δx称为路网行程时间系数，如式(8)所示.设定第i条公路临近阻断状态的单位行程时间ti,d(例如，当车辆平均速度为10 km/h时)，计算此时的行程时间系数Δi,d，称为阻塞系数，其均值Δd称为路网阻塞系数，如式(9)所示.

引用文献[17]中基于延迟行程的指标比例，设第i条高速公路的80%行程时间为ti,80，即将行程时间按照从小到大顺序排在后20%的时间均值，或行驶速度按照从小到大顺序排列在前20%的速度均值，如式(7)所示.ti,80与最短单位行程时间tmin的相对比值称为延迟系数Δi,80，其均值Δx,80称为路网延迟系数，如式(10)所示.最后利用Δx、Δd和Δx,80计算路网行程时间可靠性，如式(11)所示，其表示路网在拥堵或临近阻断等状态下能够完成出行的概率：

(8)

(9)

(10)

(11)

式中：Δx为路网行程时间系数；Δd为路网阻塞系数；Δx,80为路网延迟系数；Rt为路网行程时间可靠性；ti为第i条公路的单位行程时间；ti,min为第i条公路的最小单位行程时间；ti,d为第i条公路临近阻断状态的单位行程时间；ti,80为第i条公路的80%行程时间；n为道路条数.

1.4 路网可靠性

实际路网可靠性可由连通可靠性和行程时间可靠性表征，并由连通可靠性和行程时间可靠性加权求得，路网可靠性R的计算公式为：

R=αcRc+αtRt

(12)

式中：αc为连通可靠性的权重；αt为行程时间可靠性的权重；αc+αt=1.

2 高速公路网建模及拓扑指标计算

对于某区域高速公路网，对其32条公路进行标号，如图1所示.

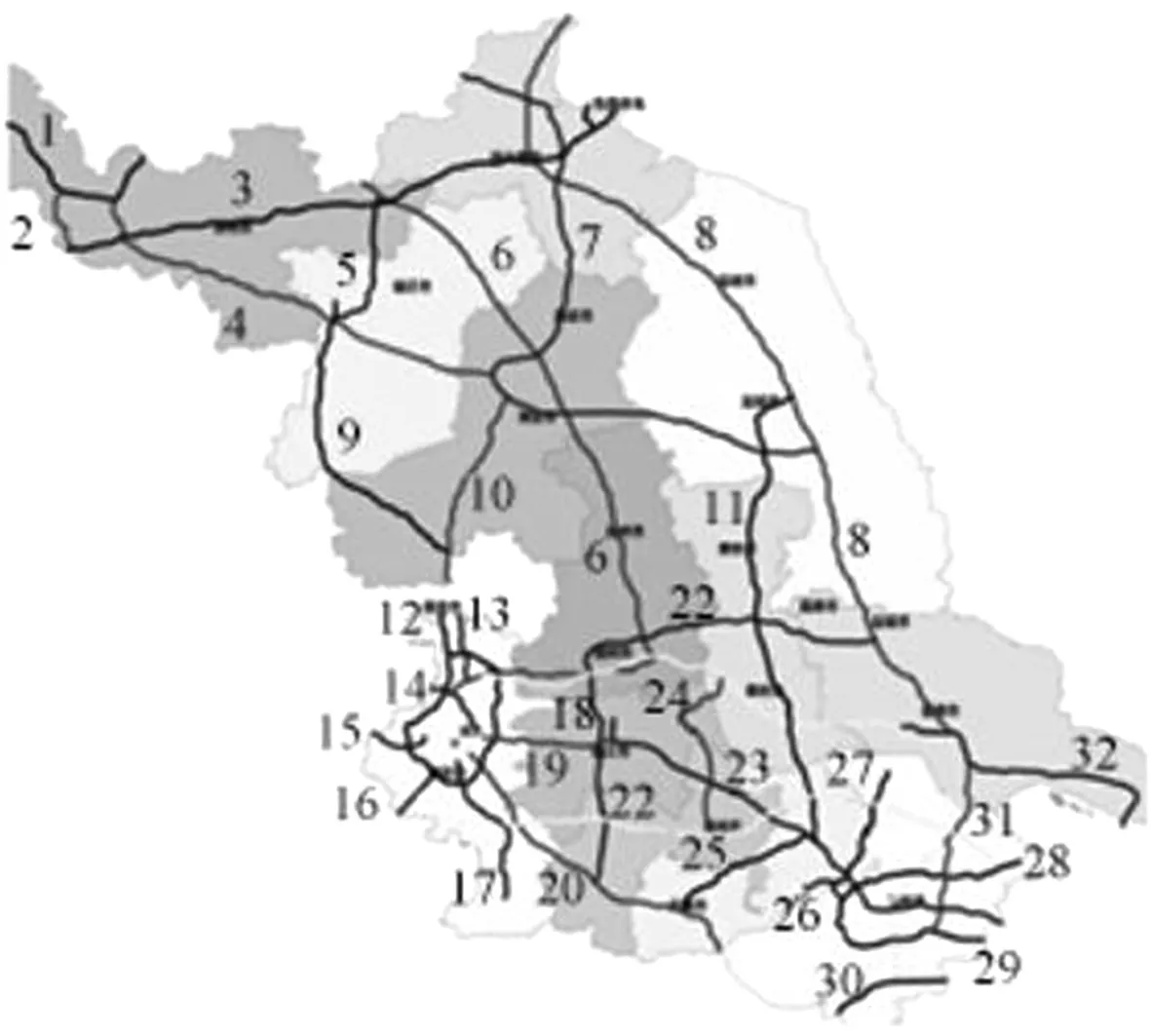
图1 区域高速路网标号图

利用对偶法得到区域高速路网拓扑结构，如图2所示.

图2 区域高速路网对偶拓扑图

利用Ucinet软件计算拓扑网络关于各条道路节点度指标，具体结果如表1.

表1 高速公路网各个节点的度

节点节点度节点节点度节点节点度节点节点度129317225222102186262361161932734412920428553132219294681422273017615123931585161243323

3 路网连通可靠性分析

3.1 逐个移除节点的路网连通可靠性

在道路网络中，“攻击”可理解为道路阻断，如由自然灾害引起的道路损毁、交通事故等.分别计算随机攻击和选择攻击下逐个移除节点后的路网连通可靠性，其中随机攻击移除节点的顺序按随机产生的32个数值排序，选择攻击移除节点的顺序按节点度从大到小排序.

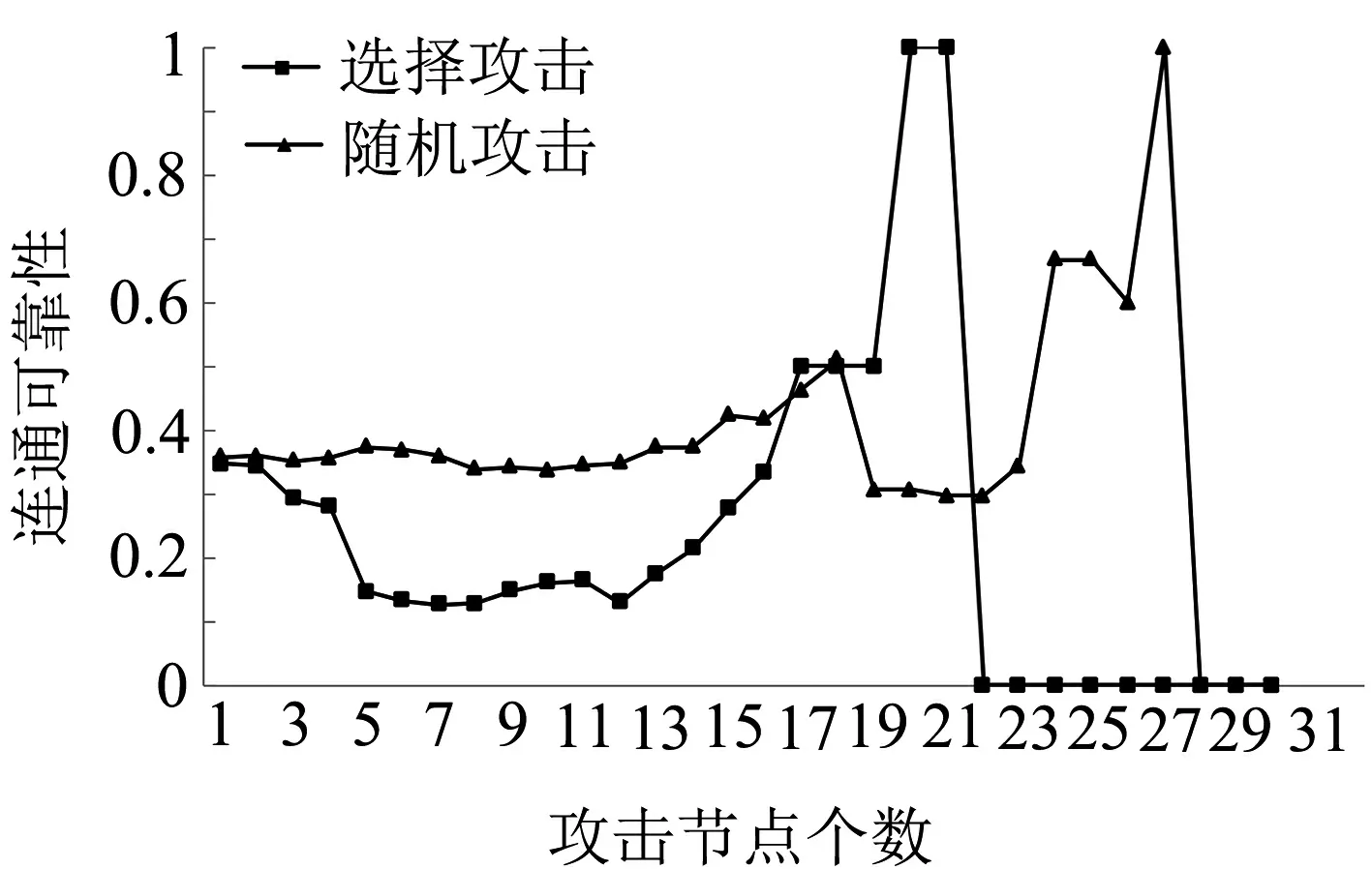
图3 选择攻击与随机攻击条件下的路网连通可靠性

由图3可知，随机攻击时经过28步可使得网络连通可靠性降为0(所有节点均孤立，表现为路网瘫痪，所有道路均互不连通)，而选择攻击经22步即可使网络连通可靠性为0；且在16步以内，选择攻击的连通可靠性始终低于随机攻击，从第17步开始，选择攻击的剩余网络是由3个两节点子网组成，而随机攻击的剩余网络是一个含11个节点的连通子网.综上，当有选择地将节点度大的点移除后，路网的连通可靠性大幅下降.而当任意移除节点时，路网的连通可靠性下降较为缓慢.

3.2 移除多个节点的路网连通可靠性

设计以下情景，当路网中有2条或3条道路阻断，统计移除节点的节点度之和，并计算和分析网络的连通可靠性变化情况，如图4所示.

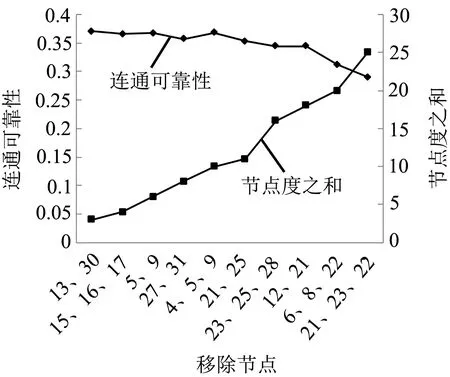
图4 移除多个节点后的连通可靠性与节点度之和的关系

由图4可知，随着移除节点的节点度之和的增加，网络连通可靠性有明显的下降趋势.在该区域实际高速公路网中，占区域总面积约1/3的南部区域，高速公路里程占了区域的一半以上，对应节点的节点度较高，高速网络的连通可靠性较高，而中北部则相反.因此，合理的提升路网密度，增加北部高速公路的数量及其连接性，可以提高区域高速公路网络的连通可靠性.

4 路网行程时间可靠性分析

连通可靠性反映了路网整体结构的连通状况，并不能反映出路网的交通运行情况，为此，假定路网车辆的不同运行速度，用行程时间来反映路网运行的可靠性.

4.1 不同行程时间系数下的行程时间可靠性

以调查时间内的路网所有车辆为统计对象，通过统计每条高速公路的运行车辆平均速度，得每条高速公路的单位行程时间，同时亦可得每条道路单位行程时间的均值及方差.设定高速公路网每条道路的车辆数相同，且假设路网所有车辆速度服从正态分布.当最大限速和临近阻断速度给定时，Rt仅与每条道路的车速有关，即不同行程时间系数下的拥挤道路行程时间可靠性和不同延迟系数下拥挤道路行程时间可靠性.

给定临近阻断状态的车辆平均速度vd=10 km/h，每条高速公路的最大限速为120 km/h，高速公路网所有道路的畅行速度均为110 km/h，用式(9)计算可得阻断系数为Δd=11.假设其中一条或多条道路处于低速状态(如介于10 km/h与110 km/h之间)，利用式(11)计算路网行程时间可靠性，此时路网的连通可靠性不变.

设定所有道路的80%速度均为50 km/h，此时单位行程时间的方差为0.605 min2.设各条道路车辆速度均值为70、90、100 km/h，对应的方差分别为0.166、0.40、0.508 min2.当部分道路的速度变化且不同速度下的低速道路条数逐渐增加时，根据不同方法计算的路网行程时间可靠性的变化规律如表2、图5、图6所示.

表2 路网行程时间可靠性变化规律(部分)

低速道路条数行程时间行程时间可靠性vi=70km/hvi,80=50km/hvi=100km/hvi,80=50km/h总均值/min总方差/min2基于延迟系数基于变异系数基于延迟行程指标1310.555 0.594 0.738 1.390 0.221 2300.565 0.584 0.736 1.353 0.206 3290.574 0.572 0.735 1.317 0.198 … ……… … … … 2930.828 0.215 0.694 0.560 0.101 3020.838 0.199 0.693 0.532 0.103 3110.847 0.182 0.691 0.504 0.103 3200.857 0.166 0.690 0.475 0.104

由表2可知，随着低速道路条数的增加，各种方法的路网行程时间可靠性均为降低趋势，基于延迟系数的方法变化最缓慢，基于变异系数的方法变化最明显.当路网低速道路条数到32条时，基于延迟系数的路网行程时间可靠性较其他两种计算方法，路网运行是相对可靠的.

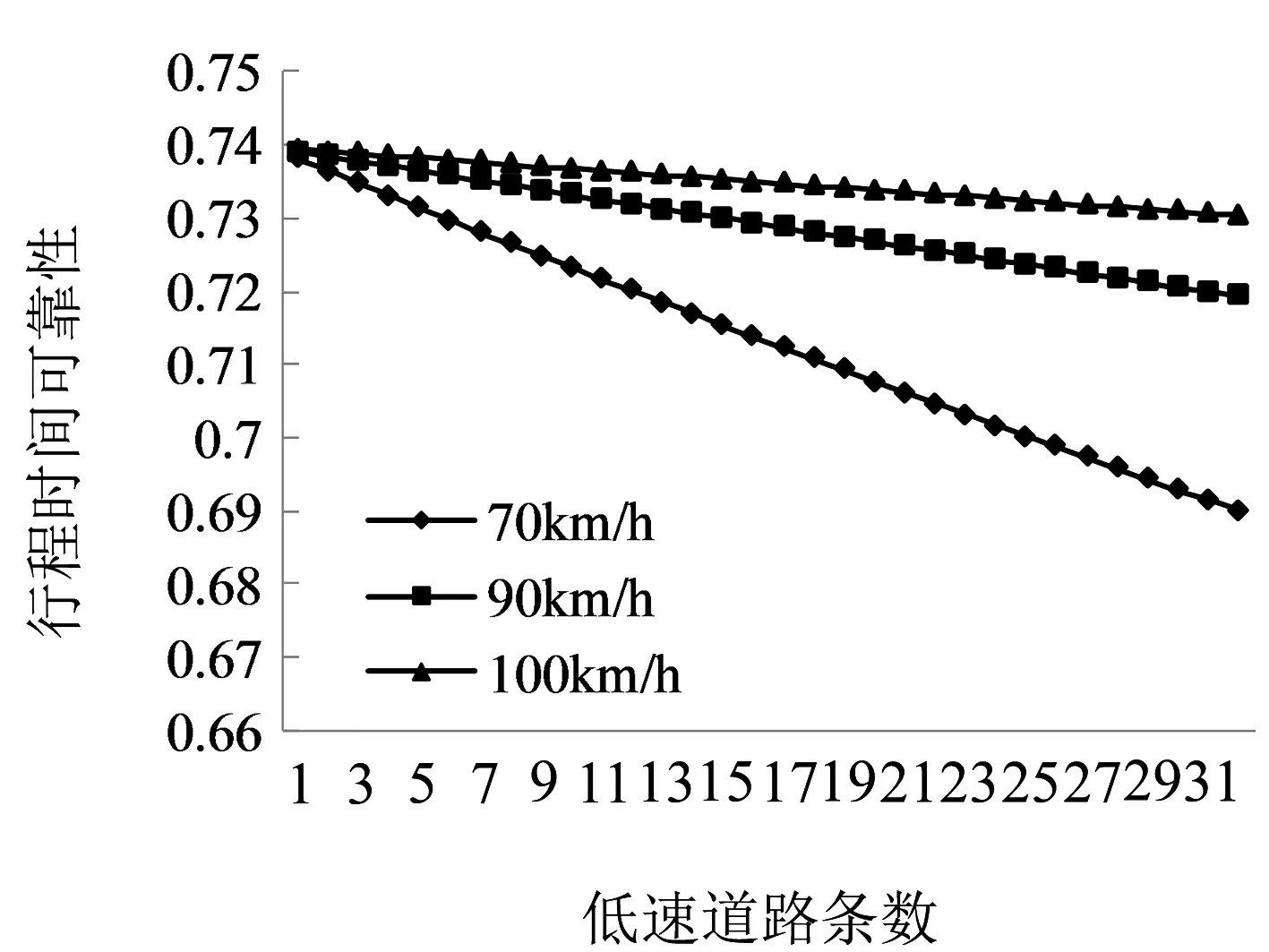
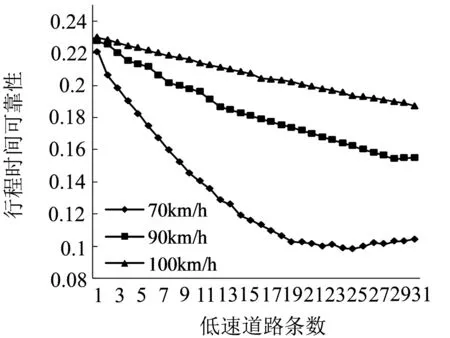
图5 基于延迟系数的行程时间可靠性

由图5可看出，在延迟系数不变的条件下，随着低速道路条数的增加，路网的行程时间可靠性降低.当速度为90 km/h时，虽有多条低速道路，但路网行程时间可靠性降低不大，甚至所有道路均拥挤时，行程时间可靠性仍为0.719；当低速值均为70 km/h时，行程 时 间 可 靠 性 为 0.69，路网运行是相对“可靠的”，而当速度降低时，路网的行程时间可靠性有加速降低的趋势，符合实际路网的运行状况.

(a) 变异系数

(b) 遭遇指数
图6 行程时间可靠性

通过对比图5、图6可看出，在延迟系数不变的条件下，当行程时间系数最小时，也就是当高速公路网所有道路的速度都达到畅行速度100 km/h时，行程时间可靠性与变异系数和遭遇指数的数值都达到最大值，且随着低速道路条数增加，行程时间可靠性降低，三者变化规律基本一致.

4.2 不同延迟系数的行程时间可靠性

当平均行驶速度为60、90和110 km/h，而80%的平均速度为50，80和100 km/h时，也就是当高速公路网的道路的单位行程时间的均值有1、0.667和0.545 min这三种情况时，且对应的方差为0.056、0.009和0.004 25 min2时，随着低速道路的条数不同，其行程时间可靠性的变化如表3、图7所示.

表3 基于延迟系数的行程时间可靠性

模拟场景低速道路条数行程时间可靠性vi,80=50vi=60vi,80=80vi=90vi,80=100vi=110基于延迟系数场景115260.858110210.845115160.833120110.82212560.812场景252520.782102020.758151520.736201020.71625520.697场景314270.86128220.841312170.823416120.80652070.791场景403200.80500320.88532000.670

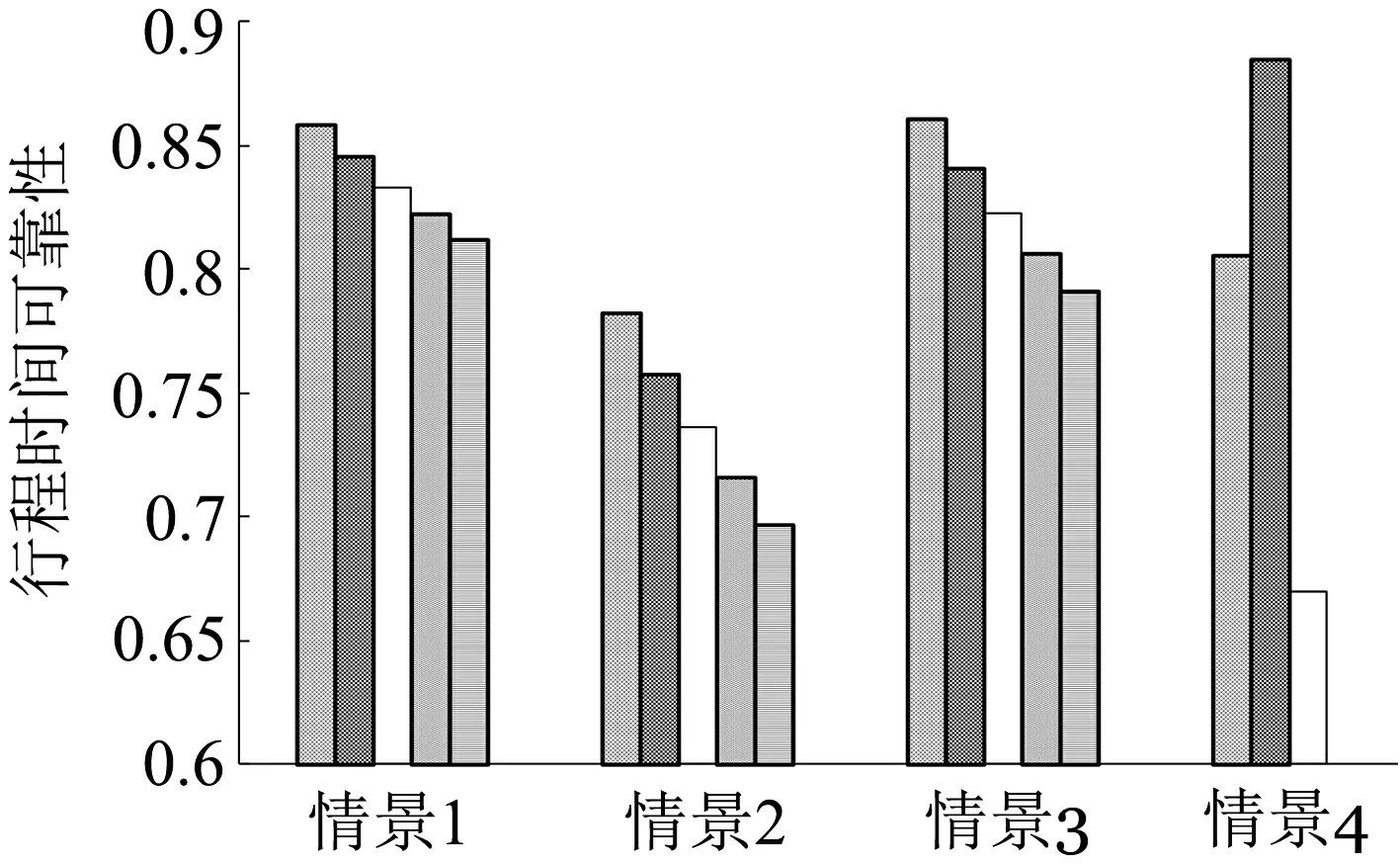
图7 基于延迟系数的行程时间可靠性

由图7可以看出，随着低速道路的条数增加，路网行程时间可靠性降低.通过模拟4可以看出，当路网的平均行驶速度和80%速度都较大时，此时路网的行程时间可靠性是最大的，并且与平均速度和80%速度都较小时的行程时间可靠性差距比较明显； 通过对比其他三种模拟情景可 以 看出，当平均速度和80%速度的道路条数相差不大的情况下，行程时间可靠性变化不大.

5 道路阻断及拥挤状况下的路网可靠性

当发生交通拥堵时人们更关注行程时间；而发生道路阻断时则更关心路网的通达状况.选取该区域高速公路网密度较高的一条道路阻断，周围有多条道路拥堵，此时假设速度为10 km/h，vi=90 km/h,vi,80=60 km/h.则路网可靠性如表4和图8所示.

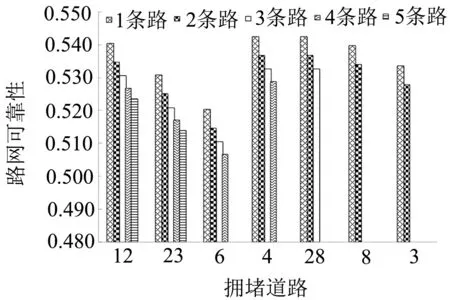
图8 道路阻断及拥挤状况下的路网可靠性

对于和其他道路连接性较好的高节点度高速公路，其道路阻断会影响邻近区域的多条道路，从而引起道路可靠性的快速下降，如节点12、23、6等对应的高速公路.对其交通诱导或应急处理就应更加重视.

表4 道路阻断及拥挤状况下的路网可靠性

阻断道路拥堵道路低速道路条数行程时间可靠性连通可靠性路网可靠性121310.955 0.3550.54113,1420.937 0.3550.53513,14,1530.923 0.3550.53113,14,15,1640.9120.3550.52713,14,15,16,1750.901 0.3550.524232210.9560.3410.53122,2420.9380.3410.525 22,24,2730.923 0.3410.52122,24,27,2940.9120.3410.517 22,24,27,29,3150.901 0.3410.514 6710.9560.3260.5217,420.9380.3260.5157,4,1030.923 0.3260.5117,4,10,340.9120.3260.5074510.9560.3580.5435,920.9380.3580.5375,9,230.923 0.3580.5335,9,2,340.9120.3580.529282310.9560.3580.54323,2920.9380.3580.53723,29,3130.9230.3580.5338310.9560.3540.5403,720.9380.3540.534 3210.9560.3450.5342,420.9380.3450.528

6 结论

本文针对现有计算行程时间可靠性方法，提出以时速为基准的路网行程时间可靠性计算思路，建立了基于延迟系数的行程时间可靠性模型并设定多种失效模式.结果显示：基于延迟系数的行程时间可靠性模型对于道路阻断和拥挤情况均适用，拥挤道路越多，路网行程时间可靠性有加速降低的趋势；随着行程时间系数和延迟系数的增加，路网行程时间可靠性有降低的趋势，且当行程时间系数和延迟系数均达到最小值时，此时的路网行程时间可靠性的值最大.

通过设计实验分析了多种失效模式下路网时间可靠性的变化规律，路网可靠性模型符合实际路网的运行情况.多种失效模式下的区域高速公路网可靠性评价，可为各省市的交通主管部门以及路网运行监测与服务中心的日常工作及应急管理提供决策依据.