空间非合作目标未知构型重建质量评估方法
李荣华,李 恒,林婷婷,王 蒙
(1. 大连交通大学机械工程学院,大连 116028;2. 上海宇航系统工程研究所,上海 201109)
0 引 言
在轨服务技术和空间碎片清除技术是太空探测技术的重要组成部分,如何在复杂空间环境下有效保护空间轨道资源,进行卫星维修、寿命延长及垃圾清理是目前亟需解决的关键问题[1]。要解决上述问题,必须获得空间非合作目标运动参数及三维形貌信息,并通过质量评估方法验证三维形貌精度,只有符合精度要求,服务航天器才能接近目标航天器实施在轨服务[2]。
目前在对空间非合作目标进行三维形貌恢复时,重建方法主要分为两种:第一种是采用序列图像的重建方式[3-4]。第二种是采用激光雷达设备获取精度较高的三维数据,再经过目标运动特性分析、点云预处理、点云配准、三维重建等技术手段,获得三维模型[5-6]。激光雷达突破了传统的成像概念和模式,具有极高速度分辨率、且工作距离长、受光照条件影响小,可以快速获取目标某个视角的三维空间信息[7]。与传统的几何建模相比,基于激光雷达的三维模型重建方法更加精确、高效,应用领域也更加广泛[8]。
三维重建完成后,重建点云是否可用于控制服务航天器对目标航天器进行在轨服务,三维模型是否可用于目标航天器的状态和关键部位识别,进而引导平台接近服务目标等,都是未知的[9]。可见,对重建结果进行质量评估是非常重要的环节。Javaheri等[10]通过选定的客观质量指标与人类质量评估的相关性进行评价。陈凤等[11]对基于序列图像获得的三维重建结果提出点云精度、重建目标识别完整性和吻合度等评估方法。Cheng等[12]提出一种双目标卷积神经网络,可以估计图像的退化类型和质量评分。Arora等[13]提出一种模型中的图像质量评估方法,包括水平和垂直质量评估以及对角线和反对角线质量评估的混合。于康龙等[14]基于结构相似度和尺度空间理论,提出一种针对超分辫率重建图像的弱参考质量评价算法。田阳等[15]对三维重构误差传播机理进行分析,给出了三维重建误差计算方法。文献[16]从噪声、密度、完整性、准确性等方面对采集的点云数据进行质量评价。陈西江等[17]将误差椭球引入到点云精度分析中,重点分析了误差椭球与点位协方差的关系。
上述评估方法多数都是针对图像序列三维重建或有已知模型进行对比分析,而对于线阵激光雷达测量未知构型的空间非合作目标重建质量评估研究相对较少,还没有统一的评判标准及评估方法。如何基于激光雷达测量的空间非合作目标未知构型三维重建结果建立有效而又简便的质量评估体系,是亟需解决的关键问题。因此,本文提出空间非合作目标未知构型重建质量评估方法。该方法着重解决空间非合作目标未知构型重建质量评估问题,确保服务航天器能够精确实施在轨服务。
1 重建质量评估流程
基于线阵激光雷达测量的空间非合作目标三维重建结果直接影响在轨服务质量。由于目标是非合作的,将无法利用重建模型与真实模型进行对比来验证重建算法是否达到预期效果。因此,针对非合作目标三维重建结果,必须建立合理、完善的评估体系,确保在轨服务能够顺利进行。因此,本文从重建点云密度、重建几何性质、重建表面完整度以及建立的多因素综合评估对空间非合作目标重建结果进行分析,获得对重建结果的满意度,其流程如图1所示。

图1 质量评估流程图Fig.1 Quality assessment flowchart
2 3σ优化拟合
这里主要认定基于激光雷达测量获得的重建点云模型表面多数为空间平面与直线,再结合人眼视觉特性判断重建点云中的平面与直线位置,构建数学模型,即在指定表面或直线上选取一定数量特征点,利用这些特征点进行拟合;然后利用3σ法则不断循环去除效果不好的数据点,优化拟合结果。
2.1 空间平面拟合
根据三维重建结果,选取模型平面点云数据(Xi,Yi,Zi),i=1,2,3,…,N,进行区域均匀采样,获得部分采样点(xi,yi,zi),i=1,2,3,…,n。依据采样点拟合出最优平面,使得每一个采样点到平面的距离的平方和最小,其流程如图2所示。

图2 平面拟合流程图Fig.2 Flow chart of plane fitting
平面方程的一般表达式为:
Ax+By+Cz+D=0,(D≠0)
(1)
两边除以D得到:
则有:
ajx+bjy+cjz+1=0,j=1,2,…,n
式中:
所有采样点到平面距离的平方和为:
(2)
只有当S最小时,才能获得最优平面,因此应满足:
(3)
化简整理:
采用克拉默法则求解线性方程组得到aj,bj,cj,即求得平面方程为:
ajx+bjy+cjz+1=0,j=1,2,…,n
(4)

图3 正态分布示意图Fig.3 Schematic diagram of normal distribution
在图3正态分布中,很容易发现:
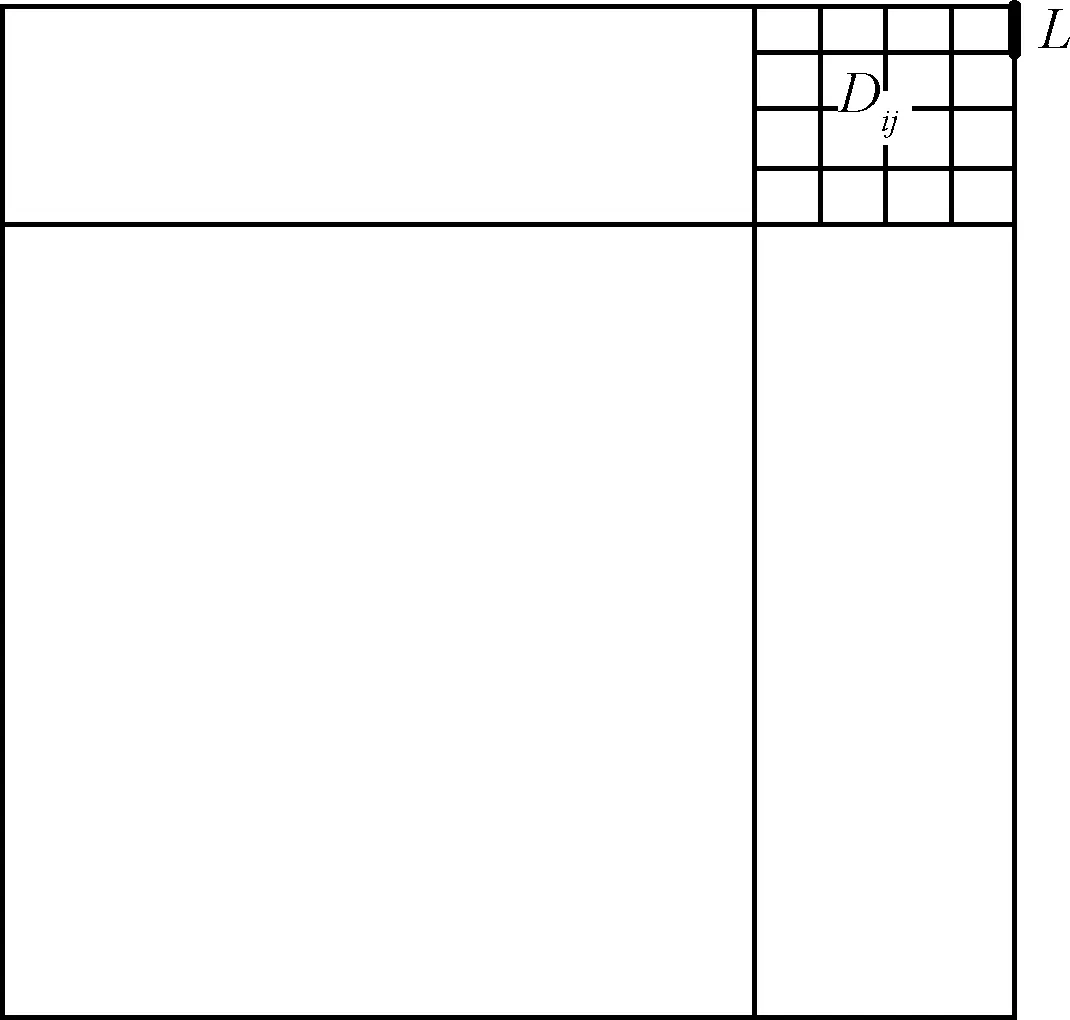
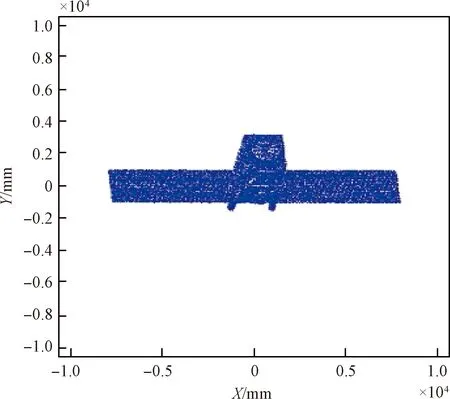
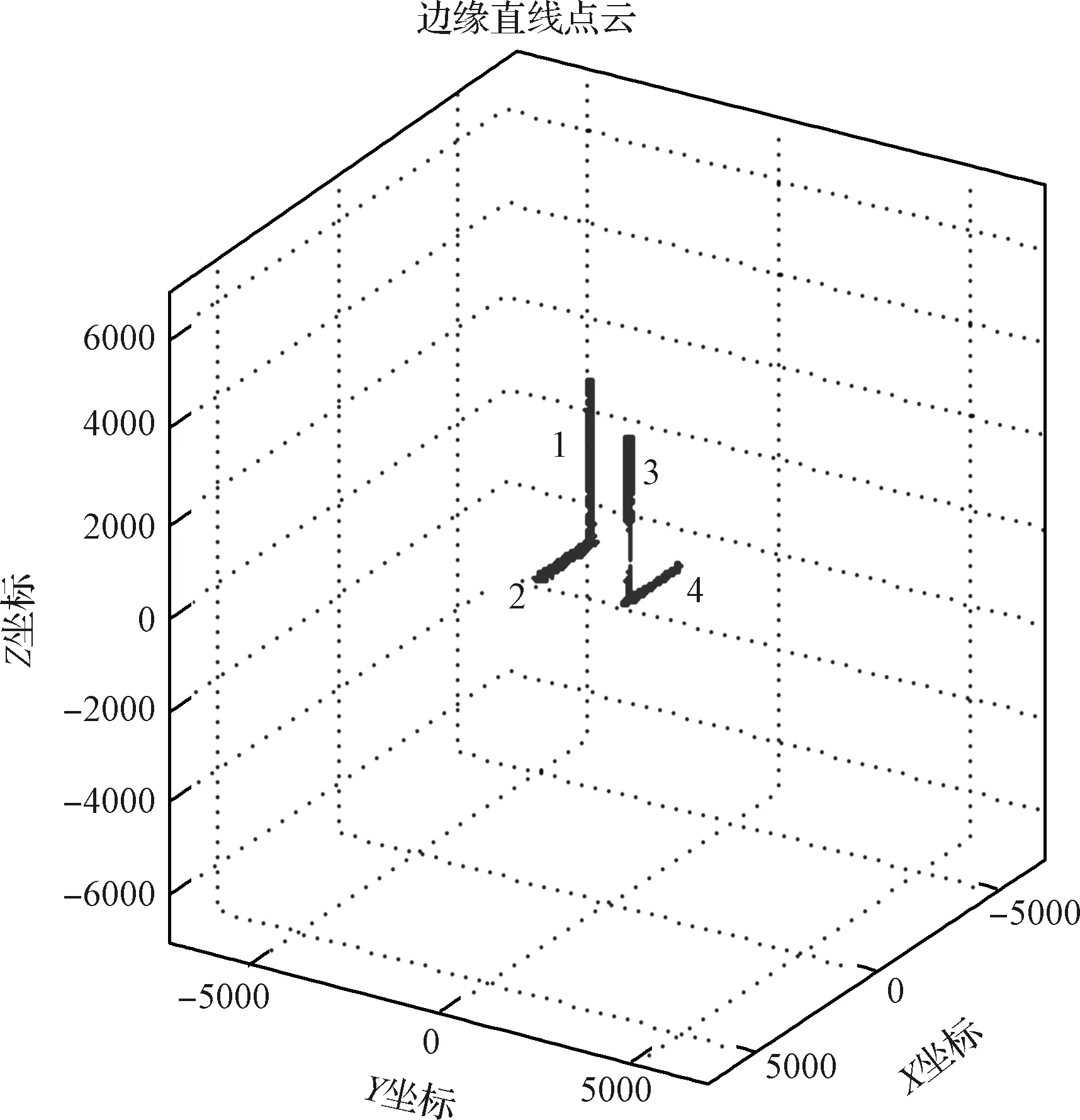
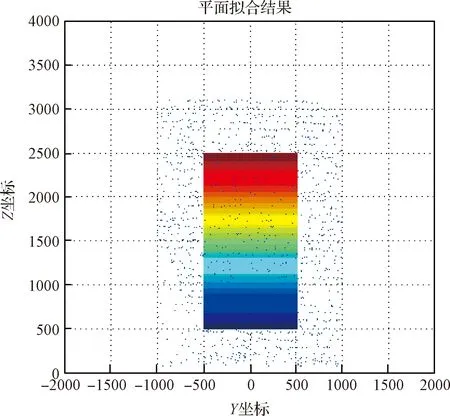
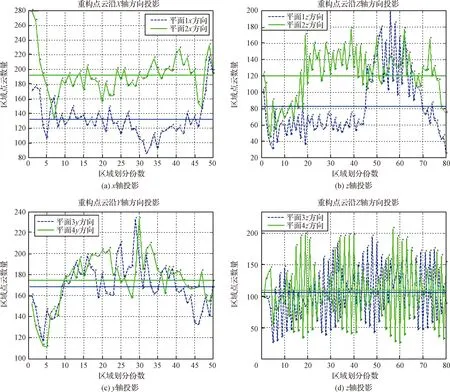
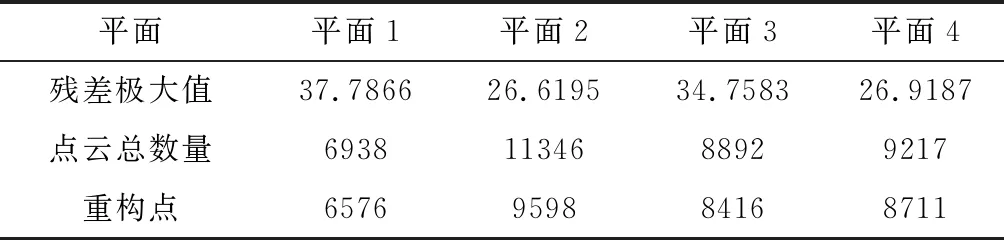
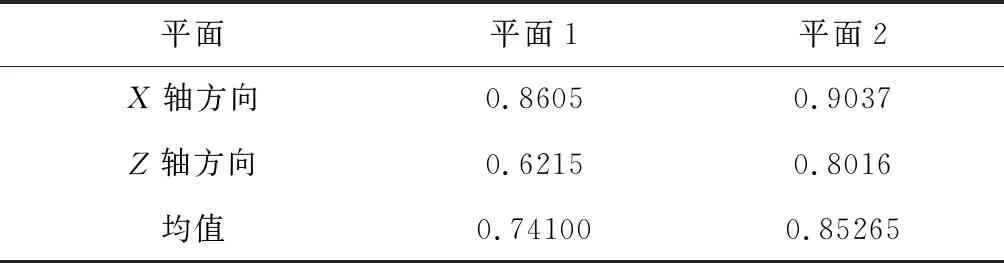
P(μ-3σ 意味着在(μ-3σ,μ+3σ]以外的概率不到0.3%,几乎不可能发生,称为小概率事件。因此,要精确得到平面方程就必须将上述获得的平面方程采用3σ法则循环剔除误差较大的点,直到没有瑕疵点参与拟合平面为止,获得最优空间平面拟合结果。 首先进行阈值设定,选取直线点云数据(Xj,Yj,Zj),j=1,2,3,…,N,再从中进行区域均匀采样获得部分采样点(xj,yj,zj),j=1,2,3,…,n。依据采样点进行空间直线拟合。 设空间直线方程为: (5) 整理获得XOZ与YOZ平面的直线射影方程: (6) 式中: 因此,空间直线可以看作上述两个平面相交的直线,如图4所示,分别对2个方程进行数据拟合。设式(7)表示按拟合方程x=az+b求得的近似值。一般地,它不同于实测值xi,两者之差由式(8)所示: (7) (8) 同理得: (9) 图4 空间直线示意图Fig.4 Schematic diagram of space line 当满足下列方程时Q值最小,即可获得方程的系数a,b,c,d的值。 (10) 令: (11) 则方程组可写成: FFTA=FX,FFTB=FY 式中: 根据n组数据点解方程组获得a,b,c,d的值,即求得直线方程。同理,采用上述3σ法则循环剔除误差较大的点,直到没有瑕疵点参与拟合直线为止,获得最优空间直线拟合结果。 空间非合作目标三维形貌结果是否满足精度要求至关重要。因此,本文建立三个评估指标以及多因素综合评估对重建结果进行评价,验证空间非合作目标重建精度及满意度。 选取重建点云平面分布范围为M×N,点云数量为Q,将其均匀划分成m×n块,用Kd表示含有点的分块个数,用Kt表示总的分块数,Md表示点云的密集程度。 (12) (13) 令Nc为分割小块的点云总数量,Dij为块内点云密度,如图5所示。其中i,j为整体点云第i行j列的小分块,设小分块正方形的边长为L,可由式(14)求得。因此小分块正方形的面积Sc为: (14) (15) 且正方形的面积也可以由点云数据的X、Y坐标值范围求得: Sc=(ymax-ymin)×(xmax-xmin) (16) 因此可得块内点云密度的计算公式为: 图5 分块点云密度计算Fig.5 Block point cloud density calculation 其中:Md对整体点云密度也有影响。可能存在点云数量多,但Md较小,意味着有较多分块不存在点云,导致局部密度很大,因此本文密度计算公式如下所示: (17) Dden受分块阈值影响,因此,本文采用先确定阈值,再自动确定m与n值。同时密度的标准为D标准,实际应用中应考虑实际情况加以选用。 采用2.1中平面拟合结果,分析平面与平面之间的平行度与垂直度关系。由于测量存在误差,导致获得的目标示意图如图6所示: 图6 目标示意图Fig.6 Schematic diagram of the target 则面与面之间夹角为: (18) 采用2.2中直线拟合结果,分析直线与直线之间的平行度与垂直度关系。则直线与直线之间夹角为: (19) 通过下式计算出模型平面所有点云数据到拟合平面距离: di=ajXi+bjYi+cjZi+1,i=1,2,…,N,j=1,2,…,n (20) 将平面沿着Z方向投影,则残差值的极大值为: max|zi-(-1-a0xi-a1yi)/a2|,i=0,1,2,…,n-1 (21) 当前观测点到拟合平面的距离小于各观测点与拟合平面残差绝对值的极值,则当前观测点在选择的表面上重构,即为表面重构点。 (22) 假设将最优结果100%对应数学描述为5,即可通过计算反求得点云密度、几何性质以及表面完整度对应的数字S密度,S几何,S完整度。 S总=S密度×γ+S几何×η+S完整度×μ (23) 其中:γ+η+μ=1 采用偏大型柯西分布和对数函数作为隶属函数,如下式所示: (24) 其中:α,β,a,b为待定系数: 将满意度划分为5个等级,分别对应数学描述为5、4、3、2、1。 当对评估结果“很满意”时,隶属度设为100%,即f(5)=100%; 当对评估结果“较满意”时,隶属度设为80%,即f(3)=80%; 当对评估结果“很不满意”时,隶属度设为1%,即f(1)=1%。 将上述结果代入上式即可求得: 所以隶属函数为: 将评估结果S总代入上式即可获得多因素评估结果满意度。 1)定义非合作目标坐标系、平台雷达坐标系、世界坐标系,明确其之间的关系;建立可测点云提取机制,精确提取某一视场角数据;依据线阵激光雷达工作原理与扫描机制,采用MATLAB模拟空间环境,建立仿真系统,实现激光雷达环绕目标做360°绕飞跟踪扫描,如图7所示;再利用坐标系之间的转换关系,获得N帧可测点云数据,如图8所示。 图7 雷达采集数据示意图Fig.7 Schematic diagram of radar acquisition data 图8 可测点云数据Fig.8 Measurable point cloud data 2)将上述获得的可测点云数据进行粗配准,再经过点云聚类分割后,采用最近迭代点(Iterative closest point,ICP)进行精配准,即可获得旋转与平移矩阵,其结果如图9所示。 图9 点云配准Fig.9 Point cloud registration 3)根据ICP点云配准方法得到的差分扫描点云数据之间的位姿增量关系,采用逆序三维重建方式,获得重建点云模型[6],如图10所示。 图10 三维重建结果Fig.10 Three-dimensional reconstruction result 根据要求,分别提取主体点云数据的四个面,如图11所示,进行评估实验。 图11 主体的四个平面点云Fig.11 Four plane point clouds of the main body 采用2.1中平面拟合方法,获得4个面的法向量为: 采用2.2中直线拟合方法,获得图12中4条直线的方向向量,见表2。 1)点云密度 本文根据需求D标准=0.02 m,设分块大小为200 mm×200 mm,将主体各平面点云划分成10×15块小正方形,各平面点云数量为6864、11233、8814、9021,通过计算获得各面点云密度见表3: 表1 各平面法向量Table 1 Normal vector of each plane 图12 直线点云Fig.12 Straight line point cloud 表2 各直线的方向向量Table 2 Direction vector of each line 表3 各平面点云密度Table 3 Point cloud density of each plane 2)几何性质 根据拟合的直线公式,获得图13的直线拟合结果,再计算出直线之间的平行度与垂直度,见表4与表5。根据拟合的平面公式,获得图14的平面拟合结果。 图13 直线拟合结果Fig.13 Straight line fitting result 表4 直线平行度Table 4 Straight line parallelism 表5 直线垂直度Table 5 Straight line perpendicularity 图14 平面拟合结果Fig.14 Plane fitting result 计算出平面之间的平行度与垂直度,见表6与表7: 表6 平面平行度Table 6 Plane parallelism 3)表面完整度 进行重构点筛选后,将平面1与2中重构点数量沿着x轴方向投影与z轴方向投影,结果如图15(a)与图15(b)所示;将平面3与4中重构点数量沿 表7 平面垂直度Table 7 Plane perpendicularity 着y轴方向与z轴方向投影,结果如图15(c)与图15(d)所示。各平面的点云总数量如表8所示。再依据表面完整度计算公式,求得平面1与2的表面完整度如表9所示,平面3与4的表面完整度如表10所示。 图15 重构点云数量投影折线图Fig.15 Reconstructed point cloud number projection line chart 表8 各平面重构点数Table 8 Number of reconstruction points for each plane 4)多因素综合评估结果 根据获得的点云密度、几何性质及表面完整度,求得对应的数字描述为: 表9 平面1与2表面完整度Table 9 Surface integrity of plane 1 and 2 表10 平面3与4表面完整度Table 10 Surface integrity of plane 3 and 4 S总=(S密度+S几何+S完整度)/3=4.467275 将S总代入式(24)中得到满意度为: f(x)=95.5889% 综上所述,本研究针对空间非合作目标重建质量评估问题,利用3σ优化法则进行平面与直线拟合,从点云密度、几何性质与表面完整度三个方面进行评估,再进行多因素综合评估获得满意度。仿真结果表明,该重建模型点云密度达到标准的概率为97.41%,表明重建结果较好;该重建模型几何性质达到标准的概率为93.72%,重建几何性质较好;该重建模型表面完整度达到标准的概率为76.9075%,是由于点云分布的比较随机,因此重建表面完整度较差一些;多因素综合评估满意度为95.5889%,表明整体重建结果较好,符合要求。该研究不仅能够验证基于线阵激光雷达测量空间非合作目标重建结果的准确性,且建立的多因素综合评估方法还为未知构型评估提供一种新的研究方向。2.2 空间直线拟合

3 空间非合作目标重建质量评估
3.1 重建点云密度
3.2 重建几何性质
3.3 重建表面完整度
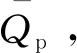
3.4 多因素综合评估

4 目标重建实验评估结果
4.1 目标三维重建结果



4.2 拟合结果

4.3 质量评估结果









5 结 论

