一种深度强化学习制导控制一体化算法
裴 培,何绍溟,王 江,林德福
(1.北京理工大学宇航学院,北京 100081;2. 北京理工大学无人飞行器自主控制研究所,北京 100081)
0 引 言
拦截导弹的制导和控制通常被当作两个回路来分开设计,内回路是产生舵指令的自动驾驶仪控制回路,外回路是生成加速度指令的制导回路[1]。内回路跟踪外回路的加速度指令产生舵偏角控制量,内外回路分开设计的主要问题是制导控制系统存在着时间滞后问题,无法拦截高速和高机动的目标。传统的外回路采用比例导引制导律设计,比例导引算法的主要思想是产生加速度指令使零控脱靶量在有限时间收敛到零[2]。虽然理论上已经证明了导引增益为3的比例导引制导律对于常值速度的飞行器是能量最优的[1],对于终端速度最大的情况也是最优的[3];并且比例导引及其多种变化形式已经被广泛的用来控制终端落角和飞行时间[4-6]。但是过去经典的制导算法的推导和理论证明都是基于忽略气动力后的线性化运动方程得到的。当考虑制导控制一体化问题的时候,由于引入了弹体气动模型,制导系统的模型就变得非线性和时变性,无法利用比例导引的形式求解。滑模控制[7]、反步法[8]和连续时间预测控制[9]等方法被用来求解制导控制一体化问题。查旭[10]针对打击固定目标,采用终端滑模理论设计制导控制一体化算法。赖超[11-12]将其扩展成为在三维情况下打击机动目标的制导控制一体化算法。虽然采用滑模控制可以实现目标拦截,但滑模控制会导致能耗增加,且容易出现控制饱和现象。这些形式的制导控制一体化算法控制律形式复杂,需要设置的参数多,针对不同的初始情况和弹体参数需要人工调整参数的取值来获得良好的制导控制表现。简化控制律的形式和自主进行参数调节是改进制导控制一体化算法的方向之一。
随着嵌入式元器件计算能力的快速发展,计算制导算法的发展引起了学者的日益关注[13]。计算制导算法不同于传统的制导律算法,它没有一个解析形式的制导律,而是通过大量的在线计算来产生制导指令。计算制导可以分为基于模型和基于数据两个类型。文献[14]中提出了一种基于模型的三维终端落角约束计算制导算法,算法基于模型预测静态规划算法[15]。模型预测静态规划算法将动态规划问题转化为静态规划问题从而提高计算效率,因此许多制导问题利用模型预测静态规划的高效性来求解,例如终端落角控制制导律[16]和再入制导[17]。然而基于模型预测静态规划方法求解制导律需要一个很好的初始猜测值来保证算法收敛[18]。
基于模型的算法要求模型的信息是完全已知的,所以基于模型优化方法的表现与模型的精度有很大的关系。制导控制一体化问题中存在着很大的模型不确定性,例如目标机动、气动不确定性等,因此不适合使用基于模型的优化方法求解。基于数据的优化算法不需要模型的精确信息,因此比较适合用来求解制导控制一体化问题。采用强化学习理论解决控制问题的研究大都应用在机器人上,很少用于解决航空航天中的制导问题。文献[19]提出了一种基于强化学习的制导算法,首先将强化学习应用到了制导领域,然而文章只考虑了一种固定的情形,鲁棒性差。深度强化学习技术还被应用于求解火星着陆制导问题[20]和再入制导问题[21]。文献[22]利用强化学习技术来学习经典的终端落角约束制导律制导增益,并将算法应用到近直线轨道的相对运动制导问题中。文献[23]利用Q学习方法根据传统比例导引制导律,提出了基于强化学习的变系数比例导引制导律,然而其需要两千次以上的迭代学习来保证结果收敛。
针对制导控制一体化问题存在的高度不确定性和控制律设计复杂的问题,本文基于无模型强化学习理论,研究了一种基于深度强化学习理论的制导控制一体化算法,算法可以通过学习自动生成制导控制智能体,无需人工进行参数调整。为了应用强化学习算法,将导弹的运动学和动力学过程建模为环境,舵偏角指令建模为智能体的行为,并且提出了权衡制导精度、能量损耗和飞行时间的奖励函数。强化学习模型框架建立后,采用深度确定性策略梯度(Deep determinstic policy gradient, DDPG)算法学习出一个从导弹观测量到舵偏角指令的行为策略。数值仿真表明提出的算法可以实现在各种不同的初始情况下的精准拦截,同传统算法相比能耗更优,能够避免控制饱和现象,并且算法对于弹体参数和气动不确定性具备良好的鲁棒性。
1 强化学习算法
强化学习的最优策略可以通过最大化值函数和最大化行为值函数得到。然而直接最大化值函数或者行为值函数都需要精确的模型信息,很难在模型不确定的情况下使用。而无模型的强化学习算法放松了对于精确模型信息的需求,因此,在存在高度模型不确定性的情况下可以使用无模型的强化学习算法。
无模型的强化学习算法可以分为值函数方法和策略梯度方法两类。值函数方法只适用于离散行为空间的情况。著名的深度Q学习[24]就属于此类。与之相比,策略梯度算法可以应用于连续控制系统的问题中。由谷歌Deepmind提出的深度确定性策略梯度算法是策略梯度算法的最新解决方案之一[25]。
1.1 深度确定性策略梯度算法
对于制导控制一体化问题,强化学习的主要目的是产生舵偏角指令控制导弹拦截机动目标。为了解决这个问题,本文使用了DDPG算法设计了一个制导控制一体化算法。DDPG是一个执行-评价算法,其基本概念框架如图1所示。

图1 DDPG算法基本概念框架图Fig.1 Basic concept of DDPG
1.2 训练DDPG智能体
为了避免在探索状态空间的过程中总回报函数陷入局部最优,DDPG在执行器网络的行为上增加一个随机噪声vt:
a′t=at+vt
(1)
式中:at为执行器网络输出的行为。
并且在后面的系统中使用这个含噪声的行为。随机噪声vt使用Ornstein-Uhlenbeck过程进行更新
(2)
式中:μv为噪声的均值;N(0,∑t)为0均值∑t方差的高斯分布;βattract是平均吸引常数,代表噪声被平均值吸引的速度;Ts是采样时间。随着训练过程经验的增加,方差∑t以速率ε指数级衰减:
Σt=Σt-1(1-ε)
(3)
DDPG的伪代码如算法1所示。

算法1 深度确定性策略梯度算法1 使用随机权重μ和w来初始化执行器和评价器网络2 使用权重μ'=μ和w'=w来初始化目标执行器和评价器网络3 初始化经验缓冲区D4 for片段=1:最大片段个数do5 for t=1:最大步数do6 执行器依据当前状态产生行为at=Aμ(st)7在行为中增加噪声来探索a't=at+vt8执行行为a't得到新的状态st+1和奖励9将转移经验e(t)=(st,at,rt,st+1)存入经验缓冲区D10从经验缓冲区D中均匀抽取组随机样本ei11计算时序差分误差δδt=Rt+ηQw'(st+1,Aμ'(st+1))-Qw(st,at)12计算损失函数L(w)L(w)=1N∑Ni=1δ2i

13 使用梯度下降法更新评价器网络-12ΔwL(w)=1N∑Ni=1δiΔwQw(si,ai)wt+1=wt-αwΔwL(w)14使用策略梯度下降法更新执行器网络ΔμJ(Aμ)=1N∑Ni=1ΔμAμ(si)ΔatQw(si,ai)μt+1=μt+αμΔμJ(Aμ)15更新目标网络μ'=τμ+(1-τ)μ'w'=τw+(1-τ)w'16if任务结束then17终止当前片段18end if19 end for20 end for
式中:s,a,r分别为强化学习马尔可夫过程中的状态量,行为和奖励,A和Q是分别由μ、μ′和w,w′参数化定义的执行器和评价器神经网络,γ为定义的权重值,τ≪1为很小的目标网络更新速率,αμ,αw分别为执行器和评价器神经网络的学习速率。
2 制导控制一体化强化学习模型建模
这个部分将制导控制问题转化到强化学习的框架中。
2.1 相对运动学模型
考虑一个二维平面寻的阶段,如图2所示。惯性坐标系由(X,Y)所示。变量的下标M和T分别代表导弹和目标。λ和r分别表示视线角和导弹目标相对距离。γ为由惯性坐标系定义的弹道倾角。速度和侧向加速度分别由V和a表示。则描述导弹和目标的相对运动关系方程可以表示为:
(4)
(5)
(6)
(7)
式中:aTraTsin(λ-γT),aTλaTcos(λ-γT)分别为目标沿着视线和垂直于视线方向的加速度;aMraMsin(λ-γM),aMλaMcos(λ-γM)分别为导弹沿着视线和垂直于视线方向的加速度。
弹道倾角和侧向加速度之间存在以下关系:
(8)
2.2 动力学模型
导弹的加速度由气动力提供,导弹的平面动力学模型可以被表示为[8,26]:
(9)
式中:α表示弹体攻角;m表示弹体质量;ωz表示弹体俯仰角速率;g是重力加速度;Jz是弹体的转动惯量;θ是俯仰角。L和M分别表示升力和俯仰力矩,可以由下式计算得到[8,26]
(10)
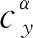
(11)
2.3 强化学习问题建模
为了使用DDPG算法求解制导控制一体化问题,需要将原问题转化到强化学习的框架中,首先要建立一个马尔可夫决策过程。式(4)~(11)的运动学和动力学方程构成了强化学习马尔可夫决策过程中的环境,环境st由过程状态可以表征为:
(12)
对于制导控制一体化问题,马尔可夫决策过程中智能体的行为定义为舵偏角指令δz。假设导弹装备有主动雷达探测器,可以测量与目标的相对距离r和视线角λ以及他们的导数。并且导弹装备有惯导装置,可以测量自身的俯仰角θ、俯仰角速率ωz和弹道倾角γM,经过组合导航算法后,可以得到攻角α,则马尔可夫决策过程中智能体的观测量ot可以定义为:
(13)
因此定义的马尔可夫决策过程是全状态可观的。
相对运动学方程(4)~(10)、过程状态(12)、智能体观测量(13)、智能体行为和一个合适的奖励函数构成了制导控制问题的马尔可夫决策过程。制导控制一体化问题的强化学习框架的概念流程图如图3所示。

图3 制导强化学习框架概念流程图Fig.3 Conceptual flowchart of the proposed guidance RL framework
2.4 定义奖励函数
采用DDPG算法求解制导控制问题最重要的部分是设计一个合适的奖励函数使导弹稳定的拦截目标。最直接的奖励函数是当导弹成功拦截目标时给智能体一个奖励,否则给智能体一个负的惩罚奖励。然而我们的实际测试表明这种简单的奖励是无效的,因为在随机初始猜想条件下导弹成功拦截目标的概率非常低,智能体在有限数量的片段性学习中几乎得不到正向激励。
因为零化零控脱靶量可以实现零脱靶量拦截[1],所以本文使用零控脱靶量来建立奖励函数。在任意时刻,零控脱靶量定义为从t时刻起,如果导弹和目标都不机动,导弹和目标最近的距离。将零控脱靶量定义为z,其形式为[26]:
(14)
舵偏角的大小直接量化了由诱导阻力导致的速度损失。考虑到这个情况,奖励函数同样需要考虑控制能耗。并且由于寻的阶段通常非常短,需要导弹快速的拦截目标。因此,将奖励函数定义如下:
Rt=Rδ+Rz+RVr+Rr
(15)
其中
(16)
(17)
(18)
(19)
式中:kδ,kz,kVr和kr是定义奖励函数的四个常数。δzmax为受导弹物理结构限制的最大允许的舵偏角,z0代表零控脱靶量的初始值。
从式(15)中可以看出,奖励函数的前两项惩罚的是归一化后的控制能耗和零控脱靶量。在奖励函数中使用归一化处理的原因是舵偏角大小和零控脱靶量具有不同的单位和尺度,很难在没有归一化的情况下直接比较。第三项rVr是激励导弹持续减少相对距离来实现快速拦截。这一项同时也对任务失败做出惩罚,因为如果在剩余飞行时间到0之后,导弹没有命中目标,导弹和目标之间的相对距离就会增加。第四项rr是当相对距离小于一个正常数rd之后给予奖励。这一项仅在导弹接近目标的时候产生作用,因此与经典优化控制问题中终端约束代价类似,用于约束终端状态。简而言之,本文提出的奖励函数允许智能体在拦截精度、能量损耗和飞行时间之间进行权衡。由于强化学习的过程具有随机性,目前针对奖励函数参数的选择没有一个定量的解析形式,但是可以通过训练结果定性的调整参数的取值。
kδ:通常选取比较小的数值,训练的首要目的是命中目标,其次是降低能耗,当训练结果保证命中目标后可以适当增大取值
kz:驱动零控脱靶量持续减少,参数取值过小零控脱靶量无法收敛到零,无法命中目标,参数取值过大训练目标变为零控脱靶量减小最快而不是零控脱靶量收敛到零。
kVr:驱动相对距离持续较少,参数取值过小无法驱动相对距离持续减少,参数取值过大训练过程无法适应相对距离先增大后减小的情况。
kr:类似终端奖励,初始值可以给的较大,参数取值过小无法命中目标,参数取值过大不利于降低控制能耗。
rd:定义为导弹的毁伤半径。
通过二分法调整参数取值,通过进行大量的数值仿真后,形成奖励函数的超参数见表1。进行训练采取的导弹速度为VM=1000 m/s,目标速度为VT=600 m/s,初始攻角为α0=0°,初始俯仰角速率为ωz0=0 (°)/s,初始俯仰角θ0等于导弹弹道倾角初始值γM0,其他初始条件参数见表2,弹体动力学参数如式(26)所示。

表1 奖励函数的超参数取值Table 1 Hyper-parameters in shaping the reward function
3 训练DDPG制导控制智能体
这个部分定义了DDPG制导控制智能体的训练过程。智能体能够直接学习控制指令δz,产生一个直接从观测量到舵偏角指令的映射:
(20)
式中:fs是一个非线性函数。
训练DDPG制导控制智能体包含三个主要步骤:1)提出训练方案;2)创建执行器和评价器网络;3)调整超参数。
3.1 提出训练方案
在本文中,考虑一个导弹迎头攻击的情况。为了更好的使用已经学习到的经验,首先采用几个特定的初始状态条件进行训练。初始条件从状态的最大值最小值中间选取,其数值见表2。首先基于这些初始条件序列的训练DDPG制导控制智能体,当智能体采用一种特定的初始状态进行训练到收敛后切换到另一种初始状态进行训练。通过大量的经验测试,我们发现提出的智能体在一种初始条件下200个片段以内就能收敛。在特定的初始条件训练完成之后,片段进行随机初始化训练,初始状态从这些状态的最小值和最大值之间均匀随机选取。这种启发式的训练方法比直接从随机状态开始训练收敛快的多。

表2 训练初始条件取值范围Table 2 Initial conditions in training
3.2 创建网络
根据原始的DDPG算法[25],使用四层全连接的神经网络来表示执行器和评价器的网络,这种四层网络结构在深度强化学习中广泛应用。这两个网络每一层的大小如表3所示。除了执行器的输出层以外,其他层的每一个神经元都由一个整流线性单元(Relu)函数激活,该函数定义为:

(21)
由于其线性特性,能够比其他非线性激活函数提供更快的收敛速度。
并且受弹体结构限制,执行器输出的行为舵偏角大小受限,因此执行器网络的输出层由双曲正切函数激活:
(22)
执行器网络使用双曲正切激活函数的优点是限制执行器输出为(-1, 1),避免控制输入饱和问题。执行器的网络输出层由常数amax进行缩放。

表3 网络层结构Table 3 Network layer size

(23)
式中:(·)0表示变量(·)的初始值,当初始值为0时,取值为1避免奇异现象。
为了解决稳定学习过程中的过度拟合问题,执行器和评价器网络都使用带L2正则化的Adam优化器来训练。在使用L2正则化的情况下,执行器和评价器的更新方式变为:
(24)
(25)

为了增加网络训练过程的稳定性,采用梯度截断来限制执行器和评价器网络的更新,也就是当梯度的范数超过了一个给定的上界ρ,梯度就被缩放到等于ρ。这种方式有助于防止训练过程中出现数值溢出或者下溢现象。
3.3 调整超参数
当导弹和目标之间的相对距离小于rm=2 m或者时间步数超过了允许的最大步数,每一个片段训练终止。本问题中DDPG算法训练使用的超参数见表4。调整超参数对于DDPG算法的性能有很大影响,并且这种调整过程在不同的应用范围内是不同的,不同问题有不同超参数集。在大量数值仿真经验总结下,给出了表中的超参数取值。

表4 超参数设置Table 4 Hyper parameters setting
4 仿真结果
仿真训练中与升力和俯仰力矩相关的参数为:
(26)
4.1 训练结果
根据训练方案,首先采取10个固定的初始条件来序列的训练DDPG制导智能体。每一种初始条件采取200个片段进行DDPG制导控制智能体训练。图4给出了前四次固定初始条件下的学习曲线。曲线中的平均奖励是最近30次片段奖励的平均值。从图中可以看出在前四次固定初始状态训练中,提出的DDPG制导控制智能体的训练结果能够在200个片段训练内收敛。当使用这些固定的初始状态训练完成之后,训练片段的初始化变为从状态量的最小值和最大值之间随机均匀取值。随机初始条件训练过程的学习曲线如图5所示。从图中可以看出即使是在随机初始条件的情况下,经过10次固定的特定初始训练条件训练之后的DDPG制导控制智能体的平均奖励仍然能在200个片段训练内收敛到一个稳态值。训练过程能够收敛的原因是智能体已经在固定初始条件的训练中得到了一些经验。在我们的数值仿真测试中,我们发现使用启发式的训练过程比使用随机初始条件开始训练的收敛速度要快的多。

图4 特定初始条件下的学习曲线Fig.4 Learning curves with some fixed characteristic initial conditions

图5 随机初始条件下的学习曲线Fig.5 Learning curves with random initial condition
为了体现在训练DDPG制导智能体的过程中对观测量和行为进行归一化处理的重要性,图6给出了第一种固定初始条件下有无归一化处理的200个片段训练平均奖励函数的对比结果。从图中可以看出使用归一化处理能够使学习过程具有更快的收敛速度和更高的平均奖励稳态值,不采取归一化处理训练曲线无法收敛。归一化处理使得观测量的每个元素的权重都相等,可以使训练过程更有效、更高效。如果没有归一化处理,各个元素之间的尺度相差非常大,例如相对距离的量级就比视线角速度大得多,不利于执行器和评价器网络的训练。

图6 有无归一化处理过程学习曲线对比Fig.6 Learning process comparison with respect to normalization
4.2 结果测试
为了测试提出的DDPG制导智能体的拦截表现,将训练得到的DDPG制导智能体应用到拦截机动目标的仿真测试中,仿真初始条件为相对距离初值r0=5000,初始弹目视线角λ0=0°,初始导弹弹道倾角为γM0=20°,初始目标弹道倾角为γT0=150°,目标常值加速度机动,加速度为20 m/s2。受弹体结构限制,舵偏角指令限制为|δz|≤δzmax。为了与传统设计方法进行对比,文中采用了两种方法进行对比,第一种是制导增益为3的比例导引制导律(Proportional navigation guidance,PNG)与自动驾驶仪组合来产生舵指令,自动驾驶仪采用极点配置法设计,第二种是采用反步法设计的制导控制一体化算法[23],仿真结果如图7所示。其中三种算法的拦截精度见表6,可以看出由于采取了大量的数据进行训练,提出的DDPG制导控制算法精度更高。从图7(a)可以看出,三种制导算法都能够成功拦截目标。攻角曲线如图7(b)所示,舵偏角曲线如图7(c)所示,提出的算法由于惩罚了舵偏角并且采用双曲正切函数作为输出层,抑制了舵偏角指令饱和现象。图7(d)中的加速度曲线表明,当反步法制导控制一体化算法得到的最大加速度约200 m/s2时,攻角约为40°,DDPG制导控制算法得到的最大加速度约为-100 m/s2时,攻角约为-20°,验证了式(11)中导弹的侧向加速度由攻角和重力加速度共同作用产生,同时,舵偏角作用下,为了得到更大的攻角,弹体姿态的运动更大,因此攻角过大不利于导弹稳定飞行,提出的制导控制智能体产生的最大攻角比传统反步法低,更利于工程实现。从图7(e)中的舵偏角指令控制能耗曲线可以看出,提出的DDPG制导算法在三种算法中能耗最优。从图中曲线可以看出提出的DDPG制导控制算法和反步法制导控制一体化算法曲线类似,但是由于惩罚了舵偏角指令,提出的制导算法得到的舵偏角比反步法制导控制一体化算法得到的舵偏角小,减小了控制能耗。

图7 目标机动情况下仿真测试曲线Fig.7 Test results with random initial conditions for non-maneuvering target
为了验证算法在工程应用的可行性,考虑到从组合导航算法中得到的数据存在噪声,在仿真过程中引入噪声,对算法进行仿真分析。定义加入的噪声满足高斯分布,其标准差的值见表5。从图8(a)中的飞行轨迹曲线可以看出提出的算法在噪声作用下仍然能拦截目标,但是由于存在噪声,脱靶量增大为1.12 m,图8(b)给出了舵偏角指令的曲线,可以看出控制量由于观测量存在的高斯噪声产生了高频抖振。
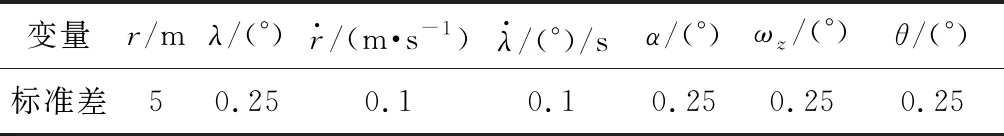
表5 噪声高斯分布标准差Table 5 Standard deviation of Gaussian distribution noise
为了测试算法对比其他两种算法的鲁棒性,对参数(26)负向拉偏40%后,采用3种算法分别进行仿真,仿真结果如图9所示。仿真结果表明,在参数进行负向拉偏后,比例导引和反步法制导控制一体化算法控制量饱和部分增加,而提出的DDPG制导控制算法由于惩罚了舵偏角指令且采取了抑制饱和的输出层,很好的抑制了饱和效应。三种算法的脱靶量见表6,可以看出参数负偏导致了制导律脱靶量增大,但是相比之下提出的算法精度仍然最高。
为了展现算法的鲁棒性和泛化性,对训练采用的参数(26)分别正向拉偏40%和负向拉偏40%后,

图9 参数负向拉偏三种算法对比仿真Fig.9 Simulation results of three guidance algorithm with parameters negative deviation
采用训练得到的制导控制智能体进行制导控制仿真,结果如图10所示。仿真结果表明在参数存在不确定性的情况下,提出的制导控制智能体仍然能保证导弹命中机动目标,制导控制智能体对气动参数和弹体参数的不确定性具有良好的鲁棒性,系统不确定性对舵偏角指令产生影响。
最后,为了更进一步测试算法的鲁棒性,初始条件在设定值的最大值最小值外浮动10%,参数(26)在标准参数的基础上正负随机偏差40%,采用不同随机初始条件对三种算法同时进行蒙特卡洛数值仿真,仿真次数设置为100次。在每个测试周期中,目标的侧向加速度为常值,均匀随机从最小值-20 m/s2和最大值20 m/s2之间取值。三种算法的脱靶量结果如图11所示,坐标信息为相对于目标位置的相对信息,同时仿真脱靶量的统计结果见表6,可以看出由于采取了大量的数据进行离线学习,提出的制导控制一体化算法在三者中精度最高。

图10 参数不确定性测试结果Fig.10 Test results with parameters uncertainty
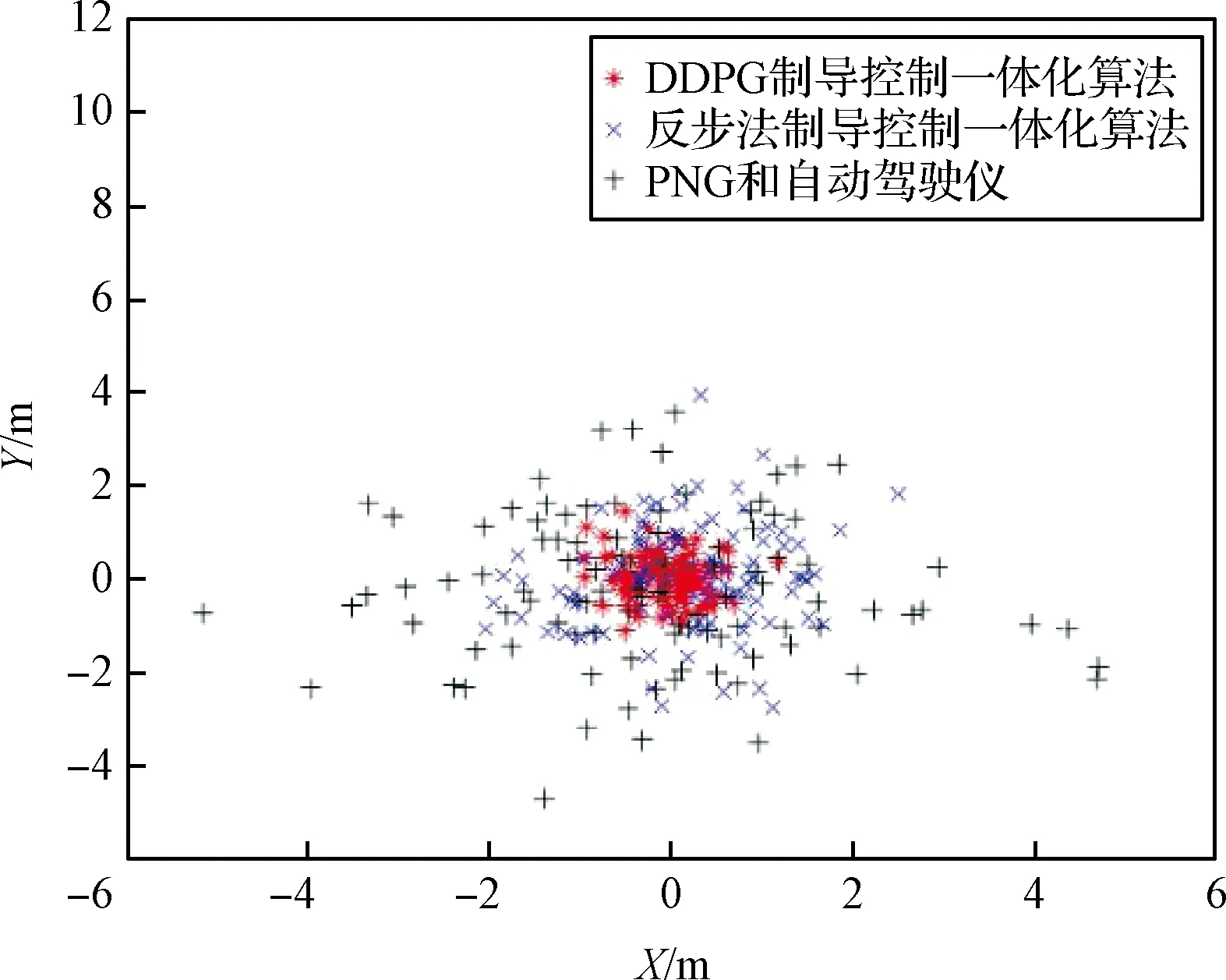
图11 三种算法蒙特卡洛仿真结果Fig.11 Monte Carlo simulation results of three guidance algorithm

表6 不同仿真情况下三种制导算法脱靶量数值Table 6 Missdistance of three guidance algorithm for different simulation cases
5 结 论
本文基于深度强化学习理论提出了一个针对导弹目标拦截问题的制导控制一体化算法。将制导控制一体化问题转化为一个强化学习优化问题,并且提出了一种启发式的奖励函数使导弹能低能耗且快速稳定的拦截目标。采用深度确定性策略梯度算法来训练强化学习制导控制智能体,使总回报的期望最大化,生成从观测量到行为映射的确定性策略,即生成了从观测量到舵偏角指令的映射。大量的数值仿真验证了提出算法的有效性和鲁棒性,同传统制导控制设计方法对比说明了提出的算法能耗更优。

