小学数学计算教学三部曲：明意，懂理，得法

郑杏桃

【摘要】计算是数与代数领域里的重要组成部分，纵观小学12册教材，无一不涉及计算教学内容。计算能力更是学生学习数学的基础。以往，教师会用大量的练习提高学生的计算能力，而新课标提出要减少单纯的技能性训练。不训练如何才能提高计算能力呢？笔者认为该从新授课入手，使学生明确计算对象的意义，懂得计算过程的道理，从而自主概括得到计算的方法。本文以《异分母分数加法》教学为例，浅谈计算教学的普适性方法。

【关键词】小学数学;计算教学;明意;懂理;得法

整数、小数和分数的计算一脉相承，环环相扣，它们的算理相通。因此，教师可运用相同的教法教，学生也可运用相似的学法学。《异分母分数加法》是人教版小学五年级下册的教学内容，教师是在学生已熟练掌握整数、小数以及同分母分数加减法的基础上进行教学的。教学可分为明意、懂理、得法三个层次。

一、明意

计算就是对数按计数单位进行拆分再合并，因此，明确数的意义、理清数的结构是学会计算的前提。小学生还处于形象思维阶段，在计算新授课一开始，教师可以借助直观，帮助学生回忆数的意义，理清数的内部结构。

在教学《异分母分数加法》时，运用学生熟悉的生活垃圾分类为素材引出一个异分母分数相加的问题，学生通过自主分析数量关系，列出算式+。教师让学生观察算式并提出疑问：和分别表示什么？

生1：表示把单位1平均分成10份，有这样的3份;表示把单位1平均分成4份，有这样的1份。

师：把单位1平均分成10份和把单位1平均分成4份，每份一样大吗？

生1：不一样。

生2：表示3个，表示1个。

教师利用课件出示两个等圆，其中一个平均分成10份，涂色占3份，表示，另一个平均分成4份，涂色占1份，表示。

此环节，教师引导学生从等分和度量两个维度理解和的意义。追问学生：把单位一平均分成10份和平均分成4份，每份的大小一样吗？以及利用几何直观，以数形结合的方式呈现两个分数的图像，旨在使学生多重感受和的大小不同，为异分母分数不能直接计算作铺垫。

二、懂理

新课标指出：学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在运用知识的过程中不断巩固和深化。计算教学中，算理为算法提供理论依据，要得算法，必须懂算理。

在探究的计算方法时，学生自主尝试计算，并把各种计算方法呈现在黑板上：

三种算法，两个答案，谁对谁错让学生在小组里进行讨论评判后再全班交流。

生3：我们小组一致认为第三种算法是错的，因为都大于，再加上，更要大于。第一和第二种算法都是先把两个加数通分，再按同分母分数的计算方法计算，是对的。

师：为什么要通分呢？不通分直接算不行吗？

生4：不通分的話表示3个，再加上1个，得到4个不知道是什么了。

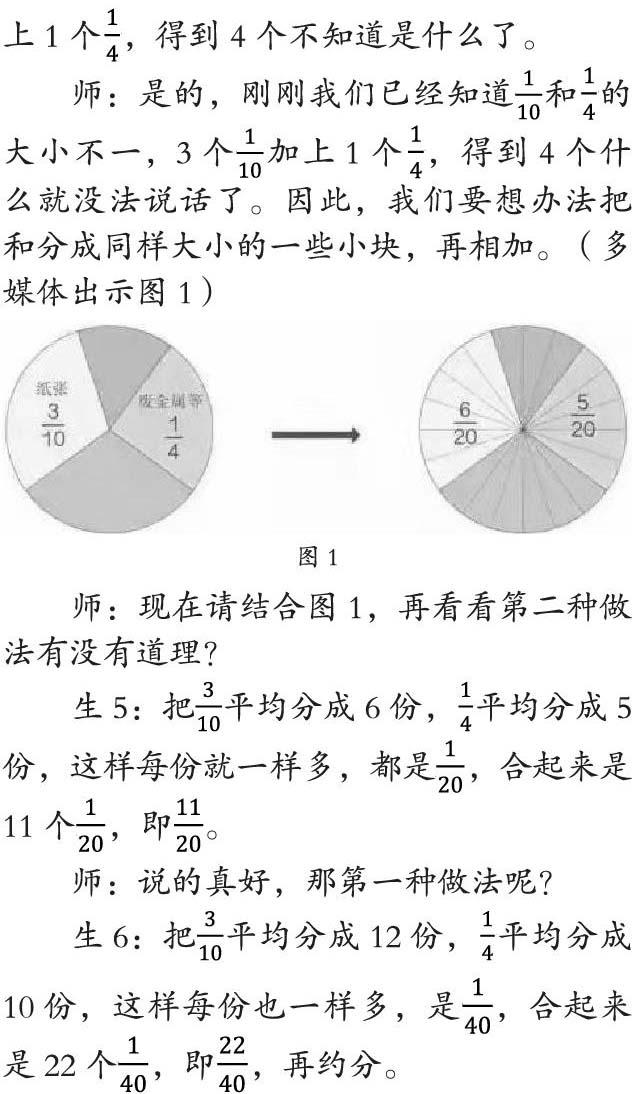
师：是的，刚刚我们已经知道和的大小不一，3个加上1个，得到4个什么就没法说话了。因此，我们要想办法把和分成同样大小的一些小块，再相加。（多媒体出示图1）

师：现在请结合图1，再看看第二种做法有没有道理？

生5：把平均分成6份，平均分成5份，这样每份就一样多，都是，合起来是11个，即。

师：说的真好，那第一种做法呢？

生6：把平均分成12份，平均分成10份，这样每份也一样多，是，合起来是22个，即，再约分。

师：结合图1说说第一种方法和第二种方法有什么异同？

生7：都是先分成同样大的小块，再计算，但两种方法分成的小块大小不一样。

师：对，分成同样大的小块其实就是对两个异分母分数进行通分，通分以后两分数的分数单位相同，分数也跟整数一样，只有在相同计数单位上的数才能计算。第二种方法通分时用的是原来两个分母的最小公倍数作为公分母，算出的结果已经是最简分数，不需化简;而第一种方法通分时没有用两分母的最小公倍数作公分母，这样算出的结果不是最简分数，因此还需化简。

异分母分数具有不同的分数单位，不能直接计算，对小学生来说是比较难理解和掌握的。本环节以数形结合的方式理解算理，呈现对应的图形，以图形来表达分数，用图形进行计算，借图形来解释算理，从而使学生在直观形象中理解算理，发展思维。

三、得法

算法就是计算的方法。计算教学的最终目标是使学生在理解算理的基础上获得计算的方法。有了以上的学习过程，在总结计算方法的时候可以让学生自主总结与归纳。

师：通过以上的计算，你能归纳出异分母分数加法的计算方法吗？

让学生先同桌交流，然后再全班交流。

生8：异分母分数加减法时，先把异分母分数通分，然后按同分母分数加法的计算方法进行计算。

师：可以怎样验算呢？

生9：可以按照整数加法的验算方法进行验算。

师：对，异分母分数相加，先通分，然后按同分母分数加法的计算方法进行计算，验算方法与整数加法的验算方法相同。

让学生用自己的语言概括异分母分数加法的计算方法是知识不断内化的过程，再通过教师对语言的提炼，让学生的认识在理解的基础上不断科学规范，最终达成知识的结构化，获得计算的方法。

四、结束语

整数、小数和分数的计算方法从表面上看截然不同，但本质是相同的，就是相同单位上的数相加或相减。因此，先明确计算对象的意义，再理清计算的道理，最后总结出计算的方法在整数、小数和分数的计算教学中同样适用。

[本文系广东省2019年教育信息化教学应用创新实践共同体项目“‘互联网+数学精准扶贫援藏创新实践共同体”（课题立项号：GDSJGTT245）研究成果]

参考文献：

[1]教育部.义务教育数学课程标准（2011年版）[S].北京师范大学出版社，2012.

[2]吴正宪.小学数学教学基本概念解读[M].教育科学出版社，2014.

[3]史宁中.基本概念与运算法则[M].高等教育出版社，2013.

责任编辑  杨  杰