超声相控阵任意点悬浮优化算法

黄俊康，邓恺潇，范千千，林家弘，何庆麟，彭 力，2

（1.华南师范大学 物理与电信工程学院，广东 广州 510006；2.华南师大（清远）科技创新研究院有限公司，广东 清远 511517）

声波可以在空气、水、生物组织等多种介质中传播.因此，可以利用超声波来产生声辐射力，用以平衡物体的重力，可以使泡沫小球、液滴、生物组织等物体稳定地悬浮.

超声悬浮技术是无容器处理的关键技术之一，在液滴蒸发［1］、析出动力学［2］、纳米微粒操控［3］、蛋白质结晶［4］等领域有广泛的应用.超声相控阵可以对轻小物体进行精细地操控，有很广泛的应用前景［5］.2015 年 Marzo［5］等人利用并比较了声镊、声涡和声杯三种声势阱的特点，拓宽了超声相控阵对粒子的操控方式，可以实现粒子的三维移动和原地旋转.在此之前，超声相控阵主要通过改变驻波的位置来实现对粒子的操控，这种方式在粒子操控范围上和操控粒子的数量上都有很大的局限性.2018年，Marzo［6］等人使用 16×16的超声相控阵实现了全息声镊，其具有与全息光镊相似的功能，它可以独立操控多个多种材质的粒子，并且适用于多种媒介（如空气、水、生物组织）.

超声相控阵对粒子精确操控的关键技术之一是求出各换能器的最优相位延迟.通过优化调控换能器的相位延迟，使各换能器处于最优相位延迟，以便在粒子悬浮位置产生稳定、抗干扰的声势阱，从而使粒子稳定地悬浮.但是在目标函数的计算上，实现难度较大.若方法使用不恰当，容易导致计算出的结果不是最优解，且计算的效率低.Marzo［6］等人使用了IB算法对相位延迟优化计算，但IB算法优化计算相位延迟时只达到了 π/16的精度.姜兆田［7］分别使用了BFGS算法和自适应遗传算法（AGA）对相位延迟优化计算，得到了AGA算法在计算较大规模超声相控阵时比BFGS算法更具优势的结论.

本文设计了一种改进的AGA算法，其优化相位延迟的精度达π/256.将其与传统遗传算法（GA）和AGA算法比较，发现改进AGA算法具有多种优势.本文使用该算法计算了空间中4个悬浮点的目标函数，发现都有很好的优化结果，并通过计算另两种阵列模式下的目标函数，验证了该算法对阵列规模不敏感.此外，本文还搭建了超声相控阵平台，将优化算法计算得到的结果运用到对轻小物体的任意点悬浮实验中，发现实验结果与仿真结果相符合，验证了该改进AGA算法的可靠性.

1 问题分析

超声相控阵实现轻小物体的任意点悬浮一般是通过控制各个换能器，使它们的相位处在最优相位延迟，在轻小物体位置处形成一个稳定、抗干扰的声势阱，从而实现轻小物体的稳定悬浮.目标函数是需要优化计算的函数，产生稳定、抗干扰的声势阱要求目标函数 O取得最大值［5］.

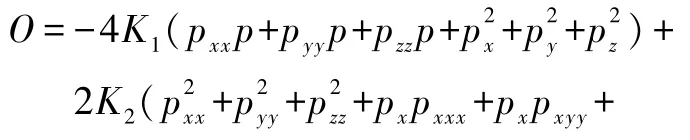
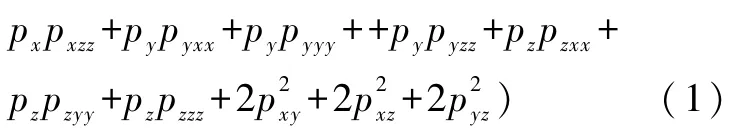
其中 K1、K2为

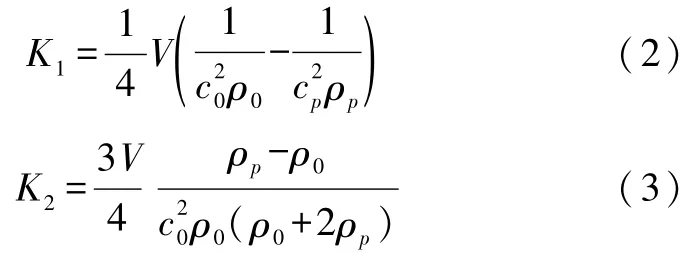
式中 V表示球形微粒的体积，ρ0是空气的密度，ρp是悬浮物体的密度，c0是媒介的声速，cp是悬浮物体中的声速.

声压 p 为［8］

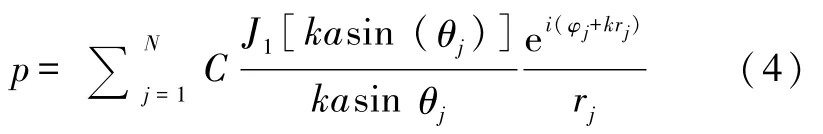
式中N为换能器个数，ω为圆频率，ua是最大振幅，a为换能器半径，θ是换能器中心和空间点的连线与法线的夹角，r为换能器中心与空间点的距离，k为波矢，φ为换能器的相位延迟，J1为一阶贝塞尔函数，图1为换能器辐射的示意图.

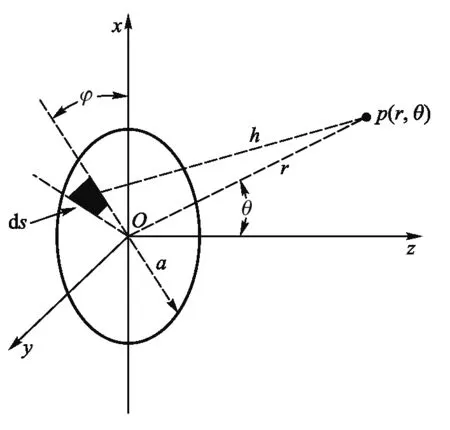
图1 换能器辐射示意图

在本文中，不需要让换能器阵列移动，因此在这里不需考虑换能器位置的变化.此时声压p只是相位延迟的函数，因此目标函数O也只是相位延迟的函数.但需要计算出各换能器的最优相位延迟，才能使目标函数O值达到最优值，从而在粒子悬浮位置产生稳定、抗干扰的声势阱.下一节将主要从个体编码、遗传算子两个方面重点介绍用于计算最优相位延迟的改进AGA算法.

2 遗传算法的改进

2.1 个体编码

遗传算法中个体的编码可采用二进制编码的方式［9］.编码出的染色体长度由换能器个数以及相位延迟精度决定.换能器的相位延迟一般是［0，2π］之间的数，若相位延迟需达到 π/2m的精度，则需要用m+1位二进制数编码.若总共有n个换能器，则染色体总长度为n（m+1）.例如，若总共有2个换能器，相位延迟分别为 φ1＝0.75π，φ2＝0.25π，精度要求为π/4，则可以用二进制数011001来表示.

为了保证计算结果有足够的精度，相位延迟精度需达到π/256.因为相位延迟在［0，2π］范围内，故每个换能器的相位延迟需用9位二进制数来表示.若有50个换能器，则50个换能器的相位延迟数据需用450位二进制数表示.这说明染色体长度应为450，可见染色体长度很长.为了加快收敛速率、使收敛更稳定和避免出现早熟现象，本文的遗传算子采用了自适应的交叉和变异算子（AGA算法与GA的区别），同时改进了选择算子（改进AGA算法与AGA算法的区别）.

2.2 改进遗传算子

在传统的遗传算法（GA）中，交叉概率 Pc和变异概率Pm固定不变.当Pc设置过大时，交叉操作容易对适应度较高的个体的结构产生破坏；当Pc设置过小时，会减慢遗传算法对最优解搜索的速度.当Pm设置过大时，遗传算法容易变成随机搜索算法，从而失去遗传算法的优势；而当Pm设置过小时，很难产生新的个体结构.

考虑到以上的种种缺陷，本文选用自适应的交叉和变异算子，该方法根据进化的情况在搜索过程中动态地调节交叉概率和变异概率，其公式为

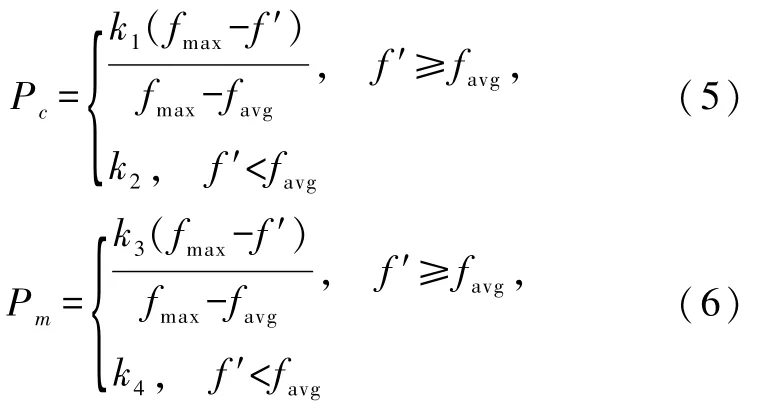
其中每代种群中的最优个体的适应度值为fmax，种群所有个体的平均适应度值为 favg，f为变异个体的适应度值，f′为准备交叉的两个个体中适应度较大的个体对应的适应度值的数值.k1、k2、k3、k4为系数，其值在［0，1］之间.

在AGA算法中，根据个体的适应度值自适应地调整 Pc和 Pm，从式（5）、式（6）可以看出，当个体适应度值接近最大适应度值时，交叉概率Pc和变异概率Pm将变小，当个体适应度值等于最大适应度值时，交叉概率Pc和变异概率Pm将变为0.这样保证了适应度高的个体的优良性状可以更好的保持下来，不被破坏，加快了算法的收敛速率；适应度低的个体交叉和变异概率较高，可以加快其进化速率，产成优良性状，避免出现早熟现象.

为了进一步提高收敛速率和收敛的稳定性，采用轮盘赌法结合精英选择策略的改进选择算子.在轮盘赌法中，个体被选择进行遗传的概率与其适应度值f成正比.适应度越高，被选中的概率越大；适应度越低，被选中的概率就越小.首先对种群中所有个体的适应度值求和:

可以计算出某个体被选中的概率为

然后计算得到某个体的累计选择概率为

选择的规则:随机生成一个［0，1］的实数 r，若r＜Qi，则选择第i个个体，否则使 i+1，然后继续进行比较.

让轮盘转动N次，每次都按照以上规则来选择个体.这样计算的结果与目的是:适应度高的个体有更高的概率将自身优良性状遗传给下一代；适应度低的个体因为遗传给下一代的概率较小，在代数不断更迭过程中，会逐渐地被淘汰，从而加快了算法的收敛速率.

精英选择策略的核心思想是:当前种群中适应度最高的个体直接替代适应度最低的个体，并且不参与本次的交叉和变异（若有最高/低适应度的个体有多个，则只取其中一个）.

从上面的分析可以看出，轮盘赌法并不能保证适应度高的个体一定会被遗传到下一代.为了最大限度地保证当前种群中适应度高的个体可以将自身优良性状遗传给下一代，使算法收敛更加稳定.因此采用轮盘赌法和精英选择策略相结合的改进选择算子，在加快算法收敛速率的同时，也能使算法收敛更加稳定.

改进AGA算法的基本步骤流程图如图2所示.

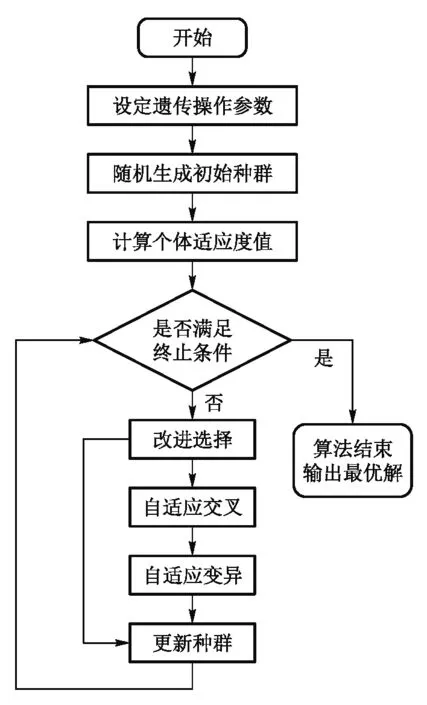
图2 改进AGA算法基本步骤流程图

3 实验结果

3.1 实验参数的设定

本文中，换能器半径为5 mm，发射超声波频率为40 kHz，空气中声速取346 m/s，由这两值可求得声波的波数为726 m-1.悬浮物为聚丙乙烯（EPS）小球，密度为 29 kg/m3，声波在 EPS中传播速率为900 m/s，空气的密度为 1.18 kg/m3.因为在本实验中目标函数只需取相对值，所以 K1、K2、C取相对值，分别为:1.759×10-16、2.945×10-16.种群规模一般设置在30～160范围内，本文综合考虑了算法最优解的搜索效率和计算时间，将种群规模设置为50［9］，并将遗传算子参数 k1、k2、k3、k4分别设为 0.7、0.2、0.4、0.2，并采用随机生成的方式初始化种群.

3.2 改进AGA算法测试

分别使用改进AGA算法、AGA算法和GA算法计算相同的目标函数，得到三者的执行结果如图3所示.

从图3中可见，AGA算法在收敛速率和最终解两方面都优于GA算法，说明自适应的交叉和变异算子可以有效地提高算法的收敛速率和最终解最优个体的适应度值.在收敛效果方面，改进AGA算法更稳定，AGA算法收敛存在频繁跳变的情况；在最终解方面，改进 AGA算法的最优个体适应度值较AGA算法更大.所以改进遗传算子，使改进AGA算法在收敛速率、最终解最优个体的适应度值和收敛的稳定性三方面较AGA算法和GA算法更有优势.

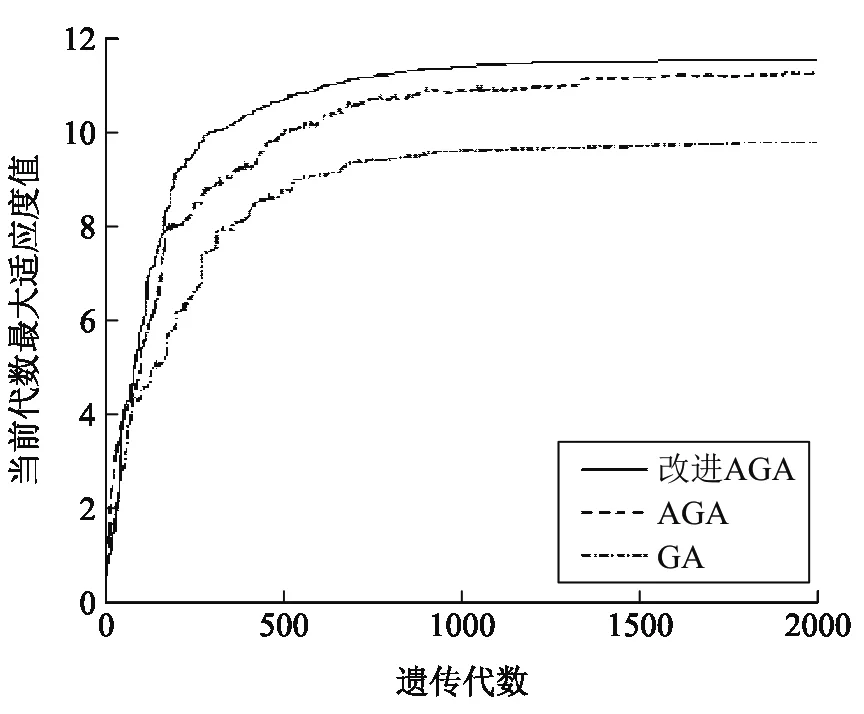
图3 三种遗传算法执行结果图

3.3 任意点悬浮实验仿真结果

为了验证改进AGA算法对空间任意悬浮点都有良好的优化效果，以上下5×5阵列为例，并在装置中轴线上取了不同高度的两点（25，25，30）mm，（25，25，45）mm，以及装置中轴线外的不同高度的两点（15，25，30）mm，（15，25，45）mm（如图 4所示，小球悬浮位置即为图4中黑点处）.使用改进AGA算法计算这4个悬浮点的各换能器的最优相位延迟，并得到了如图5所示的对应目标函数优化结果（圆圈处为小球悬浮位置）.

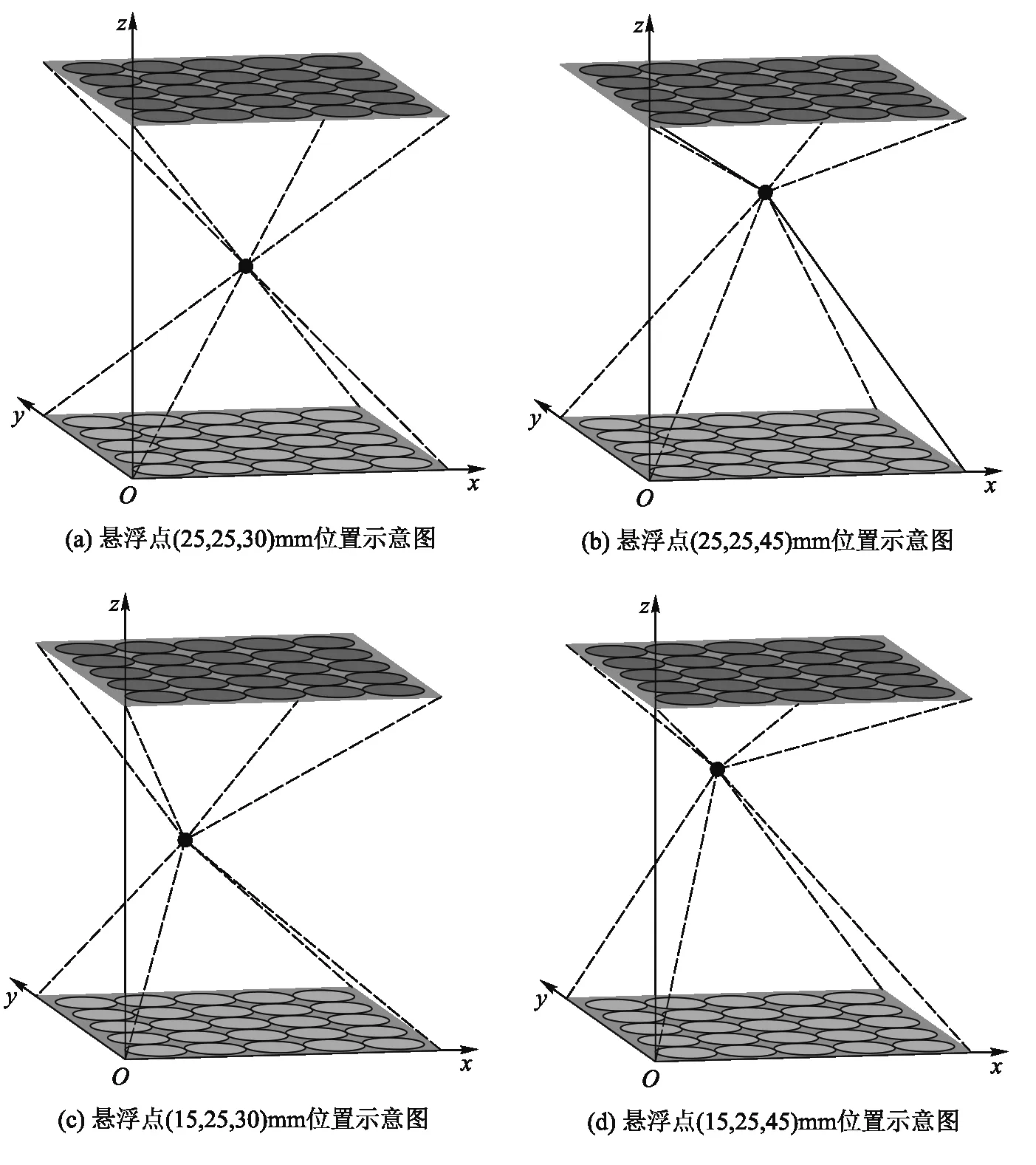
图4 悬浮位置示意图

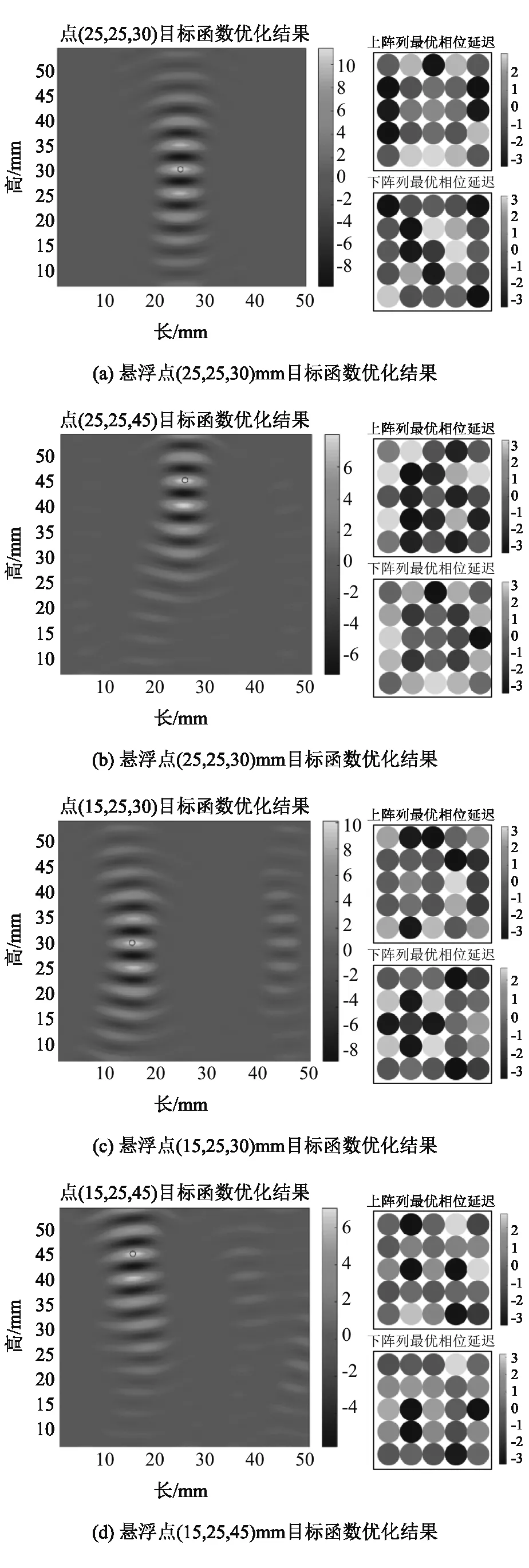
图5 任意点悬浮目标函数优化效果图

从图5中可以看出，在4个悬浮点（图中圆圈）周围目标函数取得了最优值.在悬浮点处产生了稳定、抗干扰的声势阱.

3.4 改进AGA算法敏感性分析

为了探究改进AGA算法对阵列规模的敏感性，采用了上下4×4阵列和6×6阵列两种规模的阵列（如图6所示）.小球悬浮位置即为图中黑点处，坐标分别为（20，20，30）mm，（30，30，30）mm.

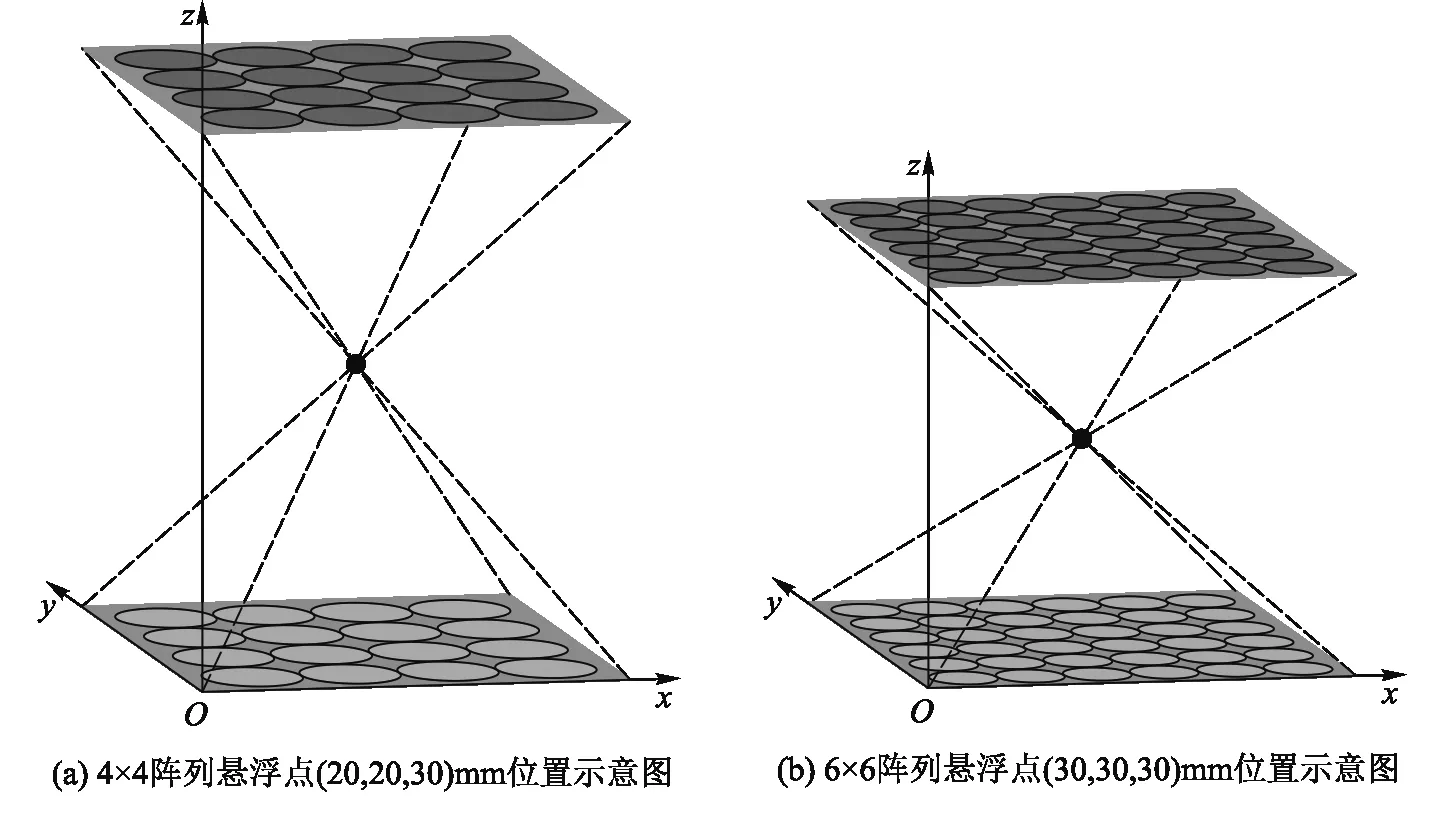
图6 两种规模阵列悬浮点位置示意图

使用改进AGA算法优化目标函数，分别计算出这两种阵列模式的各换能器最优相位延迟.目标函数的优化结果以及各换能器最优相位延迟如图7所示.

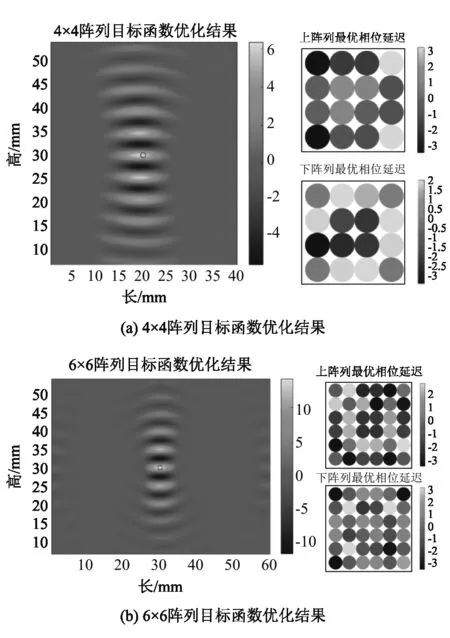
图7 不同规模阵列优化结果和最优相位延迟图

在两种阵列模式的目标函数的优化结果图中（图7），可见在小球悬浮位置处都取得了最优的目标函数值，说明该优化算法对不同规模的超声相控阵都适用，即的改进AGA算法对阵列规模不敏感.

3.5 任意点悬浮现场实验

本文搭建了上下平行5×5的超声相控阵，利用FPGA产生两组25路40 kHz的方波信号，并且方波的相位延迟控制精度可达到π/1 250.通过电脑串口可以将计算得到的各换能器最优相位延迟数据传输到FPGA上，从而实现对各个换能器相位的操控.装置示意图如图8所示.

图8 装置示意图

将各个换能器最优相位延迟数据传输给FPGA后，分别在（25，25，30）mm、（25，25，45）mm、（15，25，30）mm、（15，25，45）mm 四个位置处放置小球，经后期处理将目标函数优化结果的图像与实验拍摄的实物小球悬浮图像叠加起来（如图9所示）.从图中可见实物小球悬浮位置处于目标函数最优区域，实验结果与实验仿真结果吻合，验证了算法的可靠性.

图9 任意点悬浮实验图

4 结论

相位延迟优化算法是超声相控阵实现任意点悬浮的关键，也是难点.本文将轮盘赌法和精英选择策略相结合作为选择算子，改进了AGA算法.该改进AGA算法在对目标函数的优化上，与GA算法以及AGA算法比较，有收敛速度更快、收敛更稳定以及目标函数最优解更优的优势.本文对算法进行了敏感性分析，发现算法对阵列规模不敏感，算法适用于多种阵列规模.此外，通过实验仿真和现场实验验证了运用该算法，能够在悬浮点处产生稳定且抗干扰的声势阱，从而实现轻小物体的任意点悬浮.