小磁体在金属管中下落的阻尼运动研究

王铠泽，陶小平

（中国科学技术大学 物理学院，安徽 合肥 230026）

电磁阻尼是法拉第电磁感应定律预言的重要结果［1，2］，把一个小圆柱形永磁体沿竖直金属管轴线的上端放入管口，圆柱直径小于黄铜管的内径.在磁体沿铜管轴线下落的过程中，小磁体上方铜管的磁通量减小，下方铜管的磁通量增大，铜管中产生感应电流，感应电流的磁场将对下落的小磁体产生阻力作用.如铜管足够长，磁体下落到管子的一定深度后，速度将达到某一定值，在铜管中作匀速直线运动.现有的实验已经比较完整地探究了带有电磁阻尼的动力学过程［3-7］，本文在此基础上将这种运动特性用于金属电导率和小磁体磁矩的测量上，设计实验方案并对相关物理参数进行定量测量.

1 实验原理

1.1 磁场对涡流的作用力

在磁体沿黄铜管轴线下落的过程中，由于铜管所有部分以相同的速度作切割磁感线运动，所以铜管的任一部分都相当于是电源.如图1所示，铜管的内半径为 r1，外半径为 r2，满足 r2-r1＜＜r1，平均半径 a＝（r1+r2）/2，当铜管与小磁体的相对速度大小为v时，铜管中长度为Δz的任一小段沿圆周绕行一周的动生电动势为

图1 磁场对涡流的作用

式中Brz是小磁体在铜管上产生的磁感应强度的径向分量.

长为Δz的一段铜管沿圆周绕行一周的电阻为RΔL，电导为 GΔL.离轴心 r处，截面为 Δzdr沿圆周绕行一周的电导为

所以

式中ρ为铜管电阻率.

Δz段的电流为

Δz段的电流受到磁场的作用力

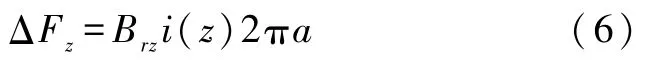
即

1.2 小磁体产生的磁感应强度

图2 铜管与运动磁体的作用力

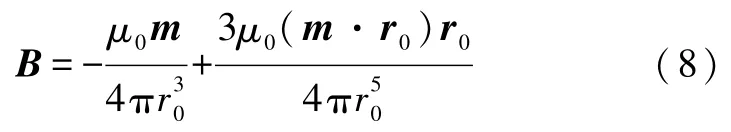
小磁体在铜管上产生的磁感应强度的径向分量为

所以

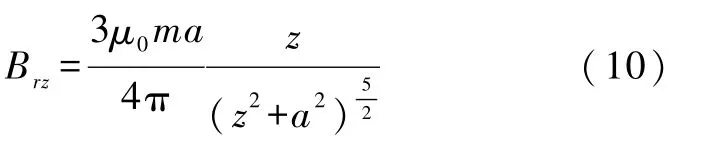
1.3 小磁体在金属管中作匀速直线运动的速度

当小磁体运动到铜管中部位置附近时，铜管所受磁体向下的作用力为

当 L＞＞a时，对式（11）积分并化简得

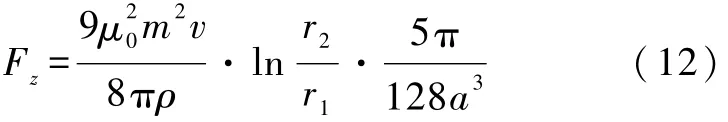
当Fz＝m0g时，小磁体作匀速直线运动的速度为

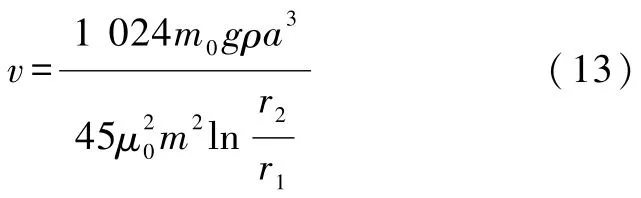
式中 m0是小磁体的质量，ρ为铜管的电阻率，r1、r2分别为铜管的内、外半径，a为铜管的平均半径，m为磁体的磁矩，μ0为真空中的磁导率，g为重力加速度.

如果能判断出小磁体在铜管中部作匀速直线运动，并测出其匀速运动的速度，则根据式（13）可确定小磁体的磁矩.

2 实验装置

实验装置如图3所示.电阻率为ρCu的黄铜管一根，铜管中部附近有一些等间距（间距为1.0 cm）的水平小孔.小圆柱磁体的直径为 8.0 mm，高度为10.0 mm，质量为10.00 g.小磁体在铜管中的下落速度，可用光电门进行测量［8］.

图3 实验装置

为测量铝的电阻率，本实验还提供一根与铜管几何尺寸相同的待测铝管.

3 实验结果及分析

3.1 确定小磁体在黄铜管中匀速下落的速度

小磁铁在铜管中下落时会受到电磁阻力最终达到匀速运动的稳态.可以通过改变光电门的位置，判断小磁体在铜管中部附近匀速下落的区间，测量出小磁体在铜管中匀速下落的速度.本次实验采取在中部附近打孔，设置光电门，两个光电门相距 l＝10 cm.测量20次所得的运动时间如表1所示.

由表1的测量数据得小磁体平均运动时间为

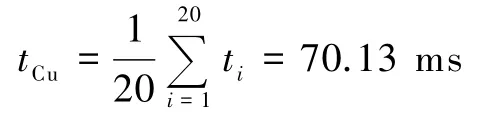
所以小磁体在铜管中匀速运动的速度为

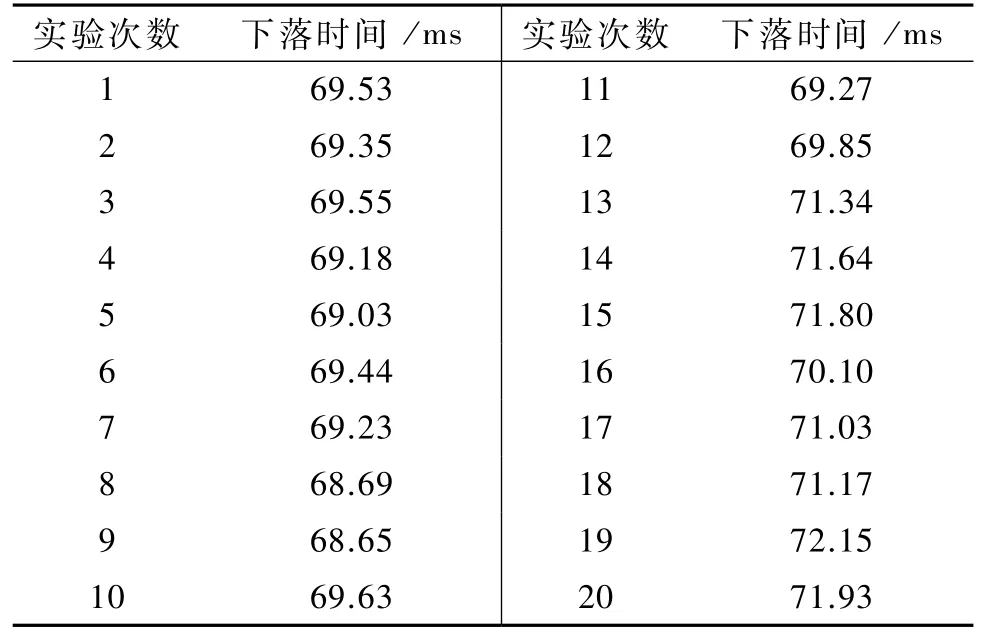
表1 小磁体在铜管中运动时间

3.2 测量圆柱形铝管的电阻率

测量出待测铝管（与铜管具有相同几何尺寸）的长度，内、外半径以及小磁体在铝管中匀速下落的速度等物理量，在已知铜的电阻率情况下，可以确定圆柱形铝管的电阻率.

测量小磁体在铝管中下落的运动时间如表2所示.由表2得到平均运动时间为

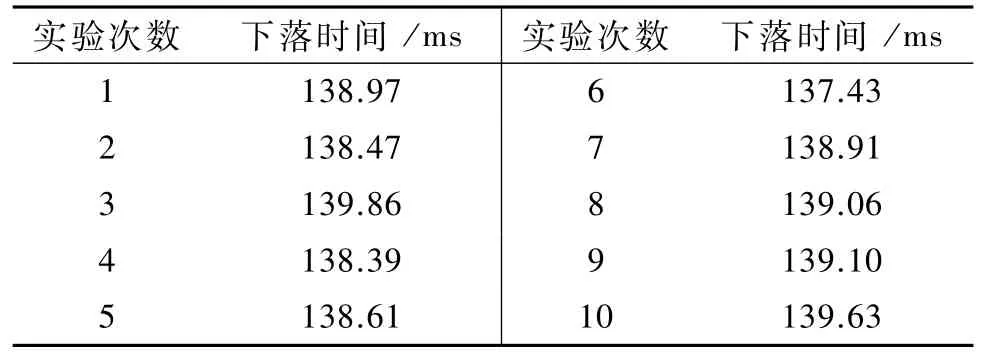
表2 小磁体在铝管中运动时间

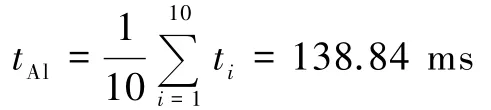
所以小磁体在铝管中匀速运动的速度为

根据式（13），得到黄铜管和铝管的电阻率之比为

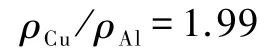
3.3 测量小磁体的磁矩

测量管的长度、内外半径以及小磁体在黄铜管中匀速下落的速度，可确定小磁体的磁矩.铜管内外半径的测量值为:r1＝5.48 mm，r2＝ 7.97 mm，黄铜的电阻率为 ρ＝7.10×10-8Ω·m.由式（13）得

代入求值得

4 结束语

本文研究了在电磁阻尼作用下小磁体在金属管中的下落运动特性，设计了可以用于测量金属电阻率和小磁体磁矩的实验方案.实验操作简单易行，数据测量具有较高精度，为磁矩和金属电阻率等物理量的测量提供了实验方法.