离散型（s，S）随机存储模型中有关问题的教学思考

周亚平，郭晓龙，吴春旭

（中国科学技术大学管理学院，安徽 合肥 230026）

存储论是运筹学的重要内容，在库存管理决策中有着广泛的应用。对于随机性存储问题，可供选择的策略主要有（1）定期订货；（2）定点订货；（3）定期订货与定点订货相结合，即（s，S）型存储策略。（s，S）型存储模型是随机性存储问题中的重要模型，其基本假设是：决策者每隔一段时间检查一次库存，如果库存量高于s则不订货，库存量小于s则订货，使库存量达到S。该模型有两种典型的情形，一是需求量为连续型随机变量，二是需求量为离散型随机变量。在（s，S）型存储策略中，涉及存储费、缺货费和订货费。存储费和缺货费与商品数量有关，订货费则与商品数量无关。只要订货就存在一次性的订货费用，若不订货则不产生该费用。（s，S）型存储策略的基本决策思路：如果决定订货，则求出最优的库存上限S，使存储费、缺货费和订货费之和的期望值最小。考虑当库存不是太低时，是否可以不订货。其条件是，当本决策阶段不订货时，存储费和缺货费（此时不存在订货费）之和的期望值低于订货至S时各项费用之和的期望值。容易证明，这样的期初库存（本阶段不订货更有利）是存在的，满足上述条件（存储费和缺货费之和的期望值低于订货至S时的费用的期望值）的最小期初库存量为（s，S）型存储策略中的s。

作为存储问题中常用的模型，（s，S）型存储策略受到了很多学者的关注。文献[1]表明最优的最大库存量和最优的重新订购点是关于需求分布、订单成本和缺货成本的函数[1]。文献[2]提出了广义的（s，S）存储策略，并且发现在一个n周期的问题中，广义的（s，S）存储策略是最优的[2]。国内广泛使用的运筹学教材[3-6]对于离散型（s，S）存储策略的建模与求解方法存在一些可改进或可拓展之处。基于此，本文给出了离散型（s，S）存储策略的分析模型、结论的证明及求解步骤。

1 基本模型

设商品的需求量为随机离散的，可能的取值为r0，r1，r2，…，rm（从小到大排列），其概率分别为。设C1为每单位商品存储一个决策阶段产生的存储费，C2为每单位商品缺货一个决策阶段产生的缺货费，C3为订货费（与订购的商品数量无关），商品的单价为K（K＜C2）。（s，S）存储策略需要确定：（1）当期初库存小于什么水平时，必须订货；（2）如果订货，库存上限为多少？

为解决上述问题，需要确定订货时应该将库存上限控制在什么水平。将库存上限S作为被优化的变量，设期初库存为I，则本阶段订货所需要的订货费为C3+K(S-I)，需要支付的存储费的期望值为，需要支付的缺货费的期望值为，各项费用之和的期望值为

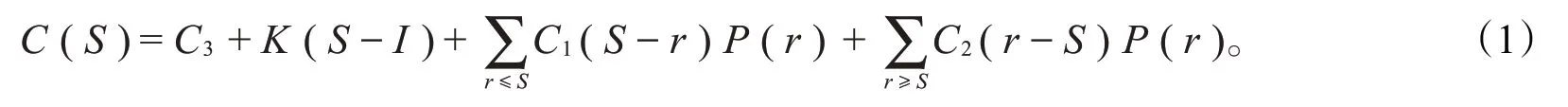
使式（1）达到最小的S即最优库存上限。在较为流行的教材中，对于该问题的处理是将最优库存上限S只从r0，r1，r2，…，rm中取值作为假设[3-6]。而事实上，S的取值也可能存在其他情况，下面讨论最优库存上限S的可能结果，并给出上述问题的具体结论。

2 模型解法

设r-1=-∞，rm+1=∞，当ri-1≤S≤ri时，

对于i=0,1,2,…,m+1，C(S)形成了m+2段直线，其斜率从K-C2（小于0）逐渐增加到K+C1（大于0），且该分段函数是连续的，具体证明过程如下。

当ri-1≤S≤ri时，

当ri≤S≤ri+1时，

对于S=ri的情况，显然S-ri=0，ri-S=0。所以，无论用式（2）或者式（3），均有C(S)=C3+，即C(S)是关于S的连续函数。又上述每一段都是关于S的线性函数，所以，C(S)为关于S的分段连续线性函数。因为函数C(S)的斜率从负到正逐渐增加，所以C(S)存在极小值，且该极小值通常在转折点（r0，r1，r2，…，rm中的一个）上出现。若C(S)在ri处取极小值，则有该点左边直线的斜率小于等于0，右边直线的斜率大于等于0。因此，当S≤ri时，≤0；而当S≥ri时，≥0，即

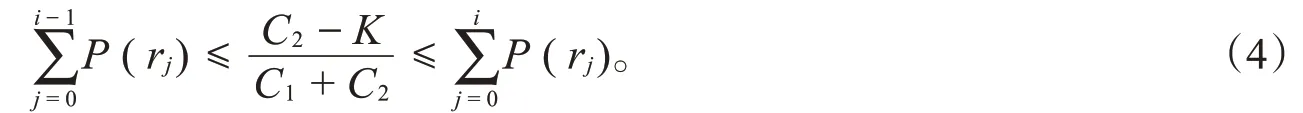
若问题中的各参数满足条件，则S=ri。注意到该条件中的左边等价于当ri-1≤S≤ri时，C(S)在这段的直线斜率小于等于0，如果此时等号成立，则C(S)在ri-1≤S≤ri的直线斜率等于0。此时，函数C(S)在整个区间ri-1≤S≤ri中的任意点均为极小值点。同理，如果，则函数C(S)在整个区间ri≤S≤ri+1中的任意点均为极小值点。

根据上面的讨论，在多数情况下，C(S)的极小值会是r0，r1，r2，…，rm中的一个。但如果出现了条件（4）的左边取等号或者右边取等号的情况，则意味着此时有无穷多个解。此时，为了保证解的唯一性，通常将条件（4）改为

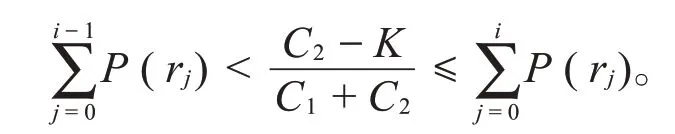
这一更改虽然保证了解的唯一性，但在个别情况（如条件（4）的左边取等号）下会导致解的遗漏。

本文模型的另外一个问题是，期初库存水平高于多少时，不订货更优？对于该问题的具体求解方法如下。

假设期初库存为s时，不订货比订货更有利，即期初库存s需要满足下列条件：

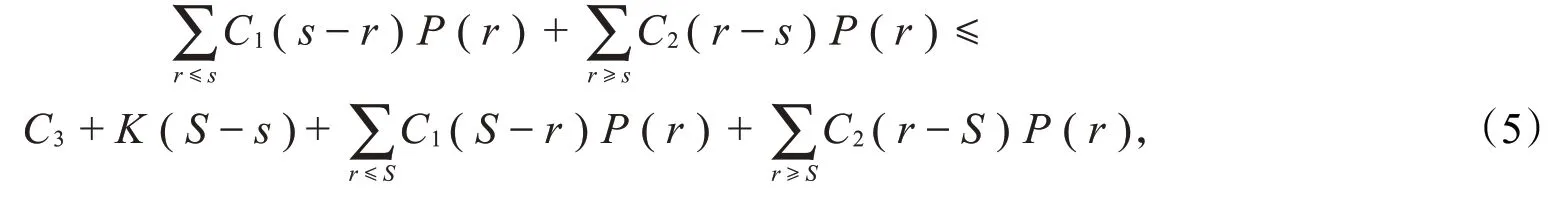
上述条件的不等号左边是期初库存为s，并且不订货时存储费与缺货费之和的期望值。显然，上述条件等价于

容易看出，满足上述条件的期初库存s是存在的，由于订货费C3＞0，当s=S时，上述条件成立。当s偏离S时（注意S是条件右边的极小值点），由于C3＞0，所以存在一个使条件（6）成立的s的取值范围（要求s＜S），满足该条件的最小的s就是要寻找的期初库存临界点。当期初库存低于该水平时，本阶段需要订货，并且将库存量增加到S是最佳的决策；当期初库存高于该水平时，本阶段不需要订货。

3 算例与结论

算例1设某公司利用塑料作原料制成产品出售，已知每箱塑料购价为1 600元，订购费C3=300元，存储费每箱C1=80元，缺货费每箱C2=2 100元，原有存储量I=20箱。已知对原料需求的概率分别为P(r=60)=0.20，P(r=80)=0.20，P(r=100)=0.40，P(r=120)=0.20，其中，r表示货物箱数，求该公司订购原料的最佳订购量。

解根据条件（4）容易求得最优库存上限S=80箱。又因原有存储量I=20箱，所以该公司应订购塑料60箱（如果订货的话）。下面求当期初库存为多少时可以不订货，即求（s，S）存储策略中的s。

由基本模型的讨论可知，是否订货的库存临界值为满足条件（6）的最小的s。经计算可得条件（6）的右边等于162 220，当s=60时，条件（6）的左边等于163 200，大于右边，条件不成立，故是否订货的库存临界值在60～80之间。由条件（6）可以求得，1 205/16为满足该条件的最小的s。因此，当期初库存大于1 205/16时，无须订货；当期初库存小于该值时，订货至库存量等于80。

算例2某厂对原料需求量的概率分别为P(r=160)=0.1，P(r=170)=0.2，P(r=180)=0.3，P(r=190)=0.3，P(r=200)=0.1，订货费C3=6 000元，K=1500元，存储费C1=100元，缺货费C2=2 200元，求该厂存储策略。

解由条件（4）容易求得最优库存上限S=180。将S=180代入条件（6）的右边，得到结果为287 400；将s=160代入条件（6）的左边，得到结果为286 200，因286 200＜287 400，故知s＜160。

而s的具体数值则根据条件（6）进行计算：当s＜160时，条件（6）的左边为1500s+2 200×[(160-s)×0.1+(170-s)×0.2+(180-s)×0.3+(190-s)×0.3+(200-s)×0.1]，令该表达式等于287 400，可得：s=1108/7。因此，该厂的存储策略为当期初库存大于1 108/7时，无须订货；当期初库存小于该值时，订货至库存量等于180。

综上所述，本文提出的模型给出了离散型（s，S）存储策略的求解方法，证明了S的取值范围与解的判别方法，拓展了s的求解方法与结论。以上两个算例说明本文的模型是有效的。因此，在实际教学过程中，要注重学生独立思考与批判性思维能力的培养，不唯书、不唯上、只唯实，这样才能提高学生分析问题和解决问题的能力。