数理融合在中学物理教育中的意义与实践简介
摘 要:物理离不开数学,数理融合、发挥数学在物理中的效能有助于培养学生的物理核心素养.但在实际教学中数理的融合度不高,且培养学生数理结合思维和应用能力的相关研究较少.本文从数理融合的现状与意义着手,通过具体路径及案例说明其对物理教学的价值.
关键词:数理融合;建模;物理核心素养;关键能力培养
中图分类号:G633.7 文献标识码:B 文章编号:1008-4134(2021)22-0026-03
基金项目:江苏省教育科学“十三五”规划重点资助课题“指向科学思维的初中物理‘证据课堂构建研究”(项目编号:E-a/2018/05).
作者简介:钱嘉(1987-),男,江苏无锡人,本科,中学二级教师,研究方向:“证据课堂的建构”研究.
1 中学物理教学数理融合的背景概述
1.1 数理融合的现状
经调查发现,教师缺少数学对于物理功能的开发,對学生数学思维方法和应用培养不够;而学生则认为数学与物理联系不大,缺乏将数学与物理专业模型结合的能力.这样的现状没有发挥数学对于物理的价值,学生数理结合思维和数学应用能力得不到提升.数学与物理自古并肩发展.随着课改的推进,数理融合在中学物理教学中的需求愈发明显.
1.2 数理融合的意义
视角不同,思维深度不同.利用数学视角审视物理问题能让思维对科学理解更深刻.在中学物理教学中进行数理融合的意义在于:
第一,数理融合遵循物理学发展规律.牛顿借助微积分描述万有引力,麦克斯韦通过纤维丛理论描述电磁波.可见数学和物理是相互促进,彼此依存的关系.
第二,物理是架设初等数学思维到高等数学思维的桥梁.大学物理具有明显的数理结合特征,学生的学习过程需要将高等数学思维和具体模型相结合,达到训练学生专业模型数学化的教学目标.这就需要教师在中学物理教学中进行数理融合训练,做好充分的准备.
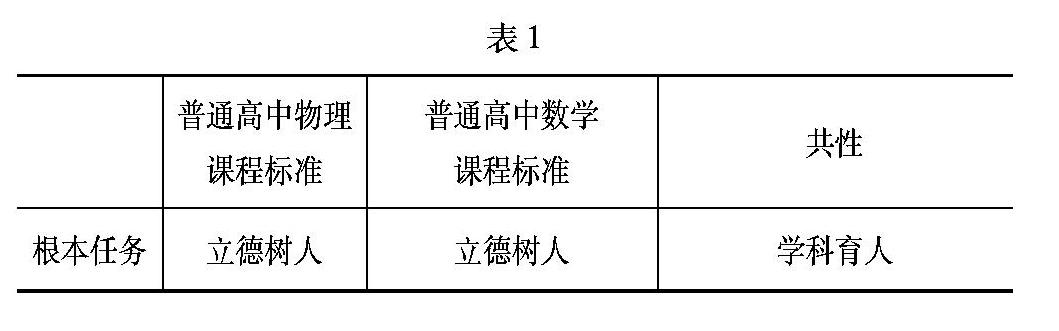
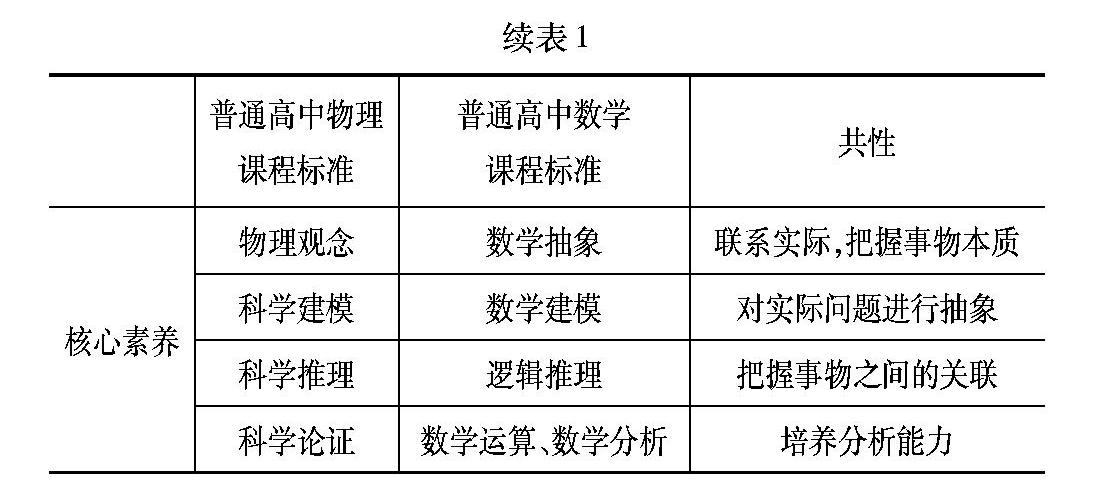
第三,数理融合有助于物理核心素养的提升.费米说过“One way, and this is the way I prefer, is to have a clear physical picture of the process that you are calculating”.物理图像(physical picture)属于物理范畴,而图像基于几何建立.对比普通高中课程标准不难发现数学与物理既相互独立,又彼此交融.物理和数学的课程标准存在很多共性(见表1).可见数理融合对学生关键能力的培养意义非凡.
2 数理融合的实践路径简介
笔者就数理融合在物理教学中的应用进行实践,并取得良好效果.本文就实践路径进行介绍,并辅以具体案例.
2.1 物理建模过渡为数学建模
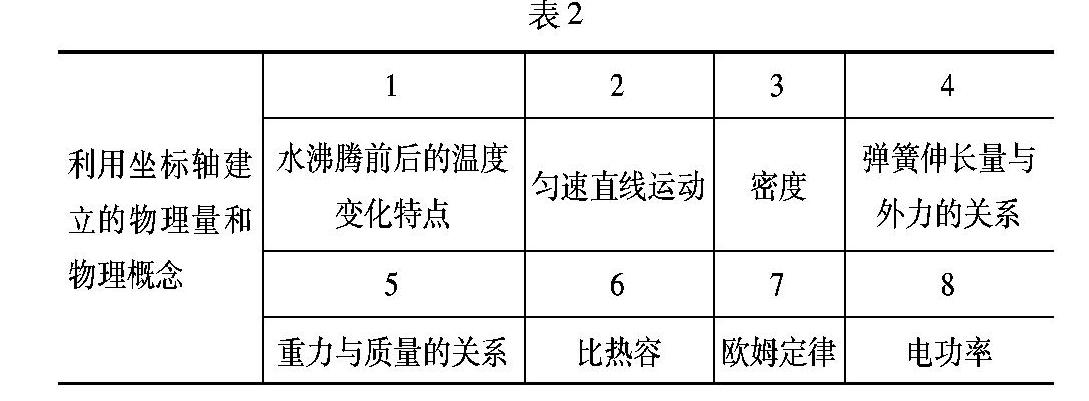
在物理教学中,规律和概念虽然内容不同,但得出流程相似,大致经历:(1)基于生活创设物理情境;(2)提取物理模型,科学建模;(3)物理模型转为数学模型;(4)分析数学模型;(5)总结物理规律和概念.运用数学模型来设计物理教学使复杂的物理问题简单化.以坐标轴为例,其贯穿于整个初中物理教学,使物理问题简洁而又深刻(以苏科版物理教材为例,见表2).
案例1 引入坐标轴建模牛顿第一定律
牛顿第一定律是初中物理最为重要的定律之一.教师在教学中最大难点在于思维的跨越:让学生从对物体受到阻力的分析跨越到对物体不受力情况的推理.在实际教学中大部分学生能就实验阻力对运动的影响(如图1所示)得出“阻力越小,小车运动得越远”的结论,但无法科学推理小车在不受力时的运动.从阻力小到不受力看似简单,但思维的跨度极大.
利用数学模型——直角坐标系科学推理牛顿第一定律使复杂的问题简单明了.由于小车在同一斜面的同一高度处由静止释放,到达水平面的初速度相同.我们用坐标轴来描述小车在不同水平面上的v-t图像(起始点选取相同的初速度).
首先分析小车在毛巾表面的运动情况.由于运动过程小车在水平面只受到摩擦力作用,因此小车做减速运动,据此画出小车在毛巾表面运动的v-t图像(如图2所示).
其次分析小车在棉布表面的运动情况.由于压力一定,接触面粗糙程度变小,小车所受摩擦力变小.所以小车在水平面运动得更远,速度减小得更慢.对比图2画出小车在棉布表面的v-t图像(如图3所示).
最后分析小车在木板表面的运动情况.同理可得小车在更为光滑的木板运动时间更长,由此画出小车在木板表面的v-t图像(如图4所示).
处理坐标轴4可得:阻力越小,直线的倾斜程度(斜率)越小.那么更为光滑的接触面v-t图像是什么样的?倾斜程度越小直至为零.当运动的小车不受力时,就保持匀速直线运动(如图5所示).
2.2 一题多解实现数理深层融合
近年,中考压轴题都可应用不同的解法得出最终结果,借助数学方法和数学思维对试题进行一题多解,更能促进数理的深层次融合.对同一问题用不同方法进行分析,如此举一反三可拓展学生的科学思维.
案例2 动态电路问题
如图6所示,电流表量程0~0.6A,电压表量程0~3V,电阻R0=5Ω,电路两端电压恒为4.5V,当滑动变阻器连入电路的电阻太小时,电路中的电流会超过电流表量程,当滑动变阻器连入电路的电阻太大时,变阻器两端电压会超过电压表量程.求:不超过电表量程,滑动变阻器连入电路的电阻范围.
解法1:第一步,画出滑动变阻器滑片P处于极限位置的等效电路如图7、图8所示(物理量对应标记在相应图像上).
第二步,对比等效电路:由图7可以看出滑动变阻器接入电路阻值最小—总电阻最小—总电流最大—定值电阻两端电压最大—滑动变阻器两端电压最小;由图8可以看出滑动变阻器接入电路阻值最大—总电阻最大—总电流最小—定值电阻两端电压最小—滑动变阻器两端电压最大.
第三步,利用欧姆定律分别计算两个电路图可得滑动变阻器连入电路的电阻范圍为2.5Ω到10Ω .
解法2:不等式是数学的重要内容,极具现实意义.我们用其分析动态电路.
I≤0.6AUV≤3V利用欧姆定律代入数据可得
I=UR总=4.5V5Ω+RP≤0.6AUV=IRP=UR总RP=4.5V5Ω+RPRP≤3V
求得:2.5Ω≤RP≤10Ω
欧姆定律是初中电学的核心,动态电路是欧姆定律的具体应用.滑动变阻器的滑片调节问题最为常见,根据学生能否解决动态电路问题即能评价学生是否理解欧姆定律.解决物理问题既能提高数学分析的能力,又能通过数学思维提升学生科学思维.
2.3 数理融合挖掘中考试题,改进评价
中考试题“一核四层四翼”评价理念,对教师日常教学具有极强导向作用.笔者从课程标准和教学目标的角度出发,数理融合挖掘中考试题,使教、学、评更具有一致性.
案例3 蹦极问题
(中考原题)如图9所示,小明在做模拟“蹦极”小实验,一根橡皮筋一端系一个小石块,另一端固定在A点,B点是橡皮筋不系小石块自然下垂时下端所在的位置,C点是小石块从A点自由释放后所能达到的最低点,关于小石块从A点到C点运动过程的说法,正确的是
A.小石块减少的重力势能全部转化为动能
B.从A点下落到B点的过程中,小石块受到重力和弹力的作用
C.从B点下落到C点的过程中,小石块的速度先增大后减小
D.小石块在C点时,受到平衡力的作用
答案:C.
评:该题基于实际情境考查学生对力与运动关系的掌握.难点在于定式思维,认为受到阻力物体就会减速,而不会定量分析动力与阻力的大小关系.为了发挥试题促学的功能,我们依据数理融合的思想重新改进试题,引发认知冲突、唤醒学生深层次思考.
(原创)如图9为小明模拟“蹦极”场景,将一根橡皮筋系一个小石块的一端固定在A点,B点是橡皮筋竖直悬挂自然长度的位置,C点是小石块从A点静止释放后所能达到的最低点.
(1)从A点下落到B点的过程中,弹性绳处于松弛状态,石块(受/不受)弹力.
(2)从B点下落到C点的过程中,石块所受的弹力(变大/变小/不变).
(3)小明绘制橡皮筋弹力与伸长量的关系图像(如图10所示),(1/2/3)能表示重力与伸长量的关系.
(4)当石块到达最低点时,重力(大于/小于/等于)弹力,受到(平衡/非平衡)力作用.
(5)从B点下落到C点的过程中,小石块的速度变化情况为.
答案:(1)不受;(2)变大;(3)3;(4)小于,非平衡;(5)先变大后变小.
设计意图:学生能认识到:(1)石块所受重力大小是恒定值而弹力大小属于变量.(2)物体所受重力小于弹力最大值.(3)重力与弹力的合力发生方向和大小的变化.(4)运动方向向下,但合力方向发生改变,据此判断运动状态也会发生改变.本题基于学生的认知规律,应用数学模型分析重力和弹力的关系,初步形成正确物理观念.
3 结语
在中学物理教学中进行数理融合,使学生深层感悟物理与数学融合之美.数理融合应趁早挖掘,这既是教学实际需求也是培养责任.良好的数学应用能力和数学思维对于物理学习至关重要.核心素养的培育绝非单学科教学所能达成.数理融合,我们一直在路上.
参考文献:
[1]谌雄文,施振刚,杨朋,贺菊香.大学物理教学的数理融合方法探讨[J].教育教学论坛,2017(30):198-199.
[2]刘炳昇.义务教育教科书(物理)[M].南京:江苏科学技术出版社,2012.
[3]钱嘉.利用一题多解提升物理核心素养——以中考一蹦极考题为例[J].中学物理,2018,36(20):62-63.
[4]寿延,亓玉田.跨学科课程的设计与实施[J].基础教育课程,2018(22):20-25.
[5]安丰亮.数理逻辑思维对中学物理的学习影响与研究[D].汉中:陕西理工大学,2019.
(收稿日期:2021-07-19)

