基于纯化学位移的同核二维正交相敏J分解核磁共振波谱

林晓晴，杜世佳，詹昊霖，黄玉清，陈 忠

基于纯化学位移的同核二维正交相敏分解核磁共振波谱

林晓晴，杜世佳，詹昊霖，黄玉清，陈 忠*

厦门大学 电子科学系，福建省等离子体与磁共振研究重点实验室，福建 厦门 361005

二维分解（2DRES）核磁共振（NMR）波谱是一种简单且用户友好的谱图表达形式，其将偶合常数和化学位移信息分离到两个正交的频率维度上．自40年前首次被提出以来，2DRES技术在脉冲序列和方法的改进，以及实际应用的进展方面一直备受关注．本文回顾了新型2DRES脉冲序列，以及用于精确测量同核偶合常数的2D编辑谱的最近进展，特别是基于纯化学位移演化机制的正交相敏2DRES谱方法及其应用，并阐述其在克服强偶合效应和磁场不均匀性等方面的能力.

核磁共振；分解谱；相敏；G-SERF；偶合常数；纯化学位移

引 言

作为一种无损高效检测技术，核磁共振（Nuclear Magnetic Resonance，NMR）已成为化合物成分分析和结构解析的重要手段，广泛用于生物、医药、化学等领域[1-8]．鉴于1H核的高天然丰度和高检测灵敏度，1H NMR目前已成为最常用的一种NMR技术．1H NMR波谱能够提供化学位移、偶合常数、谱峰积分面积和裂分模式等信息，用于物质成分分析和分子结构解析；通过增加维度，还能进行动力学分析．然而由于1H核本身有限的化学位移分布范围和丰富的偶合裂分，1H NMR谱图往往会出现谱峰拥挤甚至重叠现象，严重阻碍了谱峰的准确归属和分析．解决这一问题最直接的方式就是通过提高磁场强度来分散谱峰分布，从而缓解谱图拥挤情况，但这一方法是基于谱仪硬件的改进和提升，成本较高，并且效果相对有限．另一种行之有效的方式是通过设计特定的脉冲序列来改变谱峰分布或呈现形式，提升谱图分辨率．

目前，用于改善1H NMR谱峰拥挤的脉冲序列优化主要集中于纯化学位移方法[9-11]，这一方法的原理是消除偶合裂分，将多重谱峰简化为单峰，从而解决谱峰拥挤的问题．经历了几十年的探索和改进，相关的研究者已开发了多种不同的纯化学位移方法．而近期相关的主流技术是将选择性翻转模块与自旋回波模块相结合，实现偶合演化重聚；再通过干涉图或实时采样重构出纯化学位移演化的信号；最终经过傅里叶变换得到相敏一维纯化学位移谱图．纯化学位移技术能够大幅提高一维1H NMR谱图的分辨率，克服谱峰拥挤的问题，实现复杂样品谱峰的正确归属．然而，纯化学位移实验是以牺牲偶合为代价实现，但偶合裂分往往包含偶合常数、偶合关系等有助于结构解析和构象分析的有效信息[2,12-16]．如何在获得纯化学位移谱图的同时，又保留偶合信息，对于1H NMR谱图在复杂样品体系的更广泛应用具有重要意义，非常值得关注和研究．

二维分解（2DRES）谱[17-19]是一种能直观满足上述要求的波谱方法，其常用序列如图1所示．它能够将化学位移和偶合信息分解到两个不同维度，在得到纯化学位移信息的同时，保留偶合信息，适用于谱峰拥挤严重的复杂样品的分析[20-23]．然而，由于2DRES谱间接维的自旋回波演化形式往往会导致谱峰信号的相位扭曲，这一相位扭曲无法通过相位校正来消除，因而只能使用绝对值模式显示，从而导致谱峰强度失真和谱图分辨率降低，并造成谱线展宽的问题．特别在复杂样品检测时，2DRES谱在绝对值模式下进行45˚谱图旋转处理后，产生的谱峰变形会影响谱图分析和偶合常数的精确测量[24]．尽管45˚谱图旋转后的2DRES谱在水平1=0轴上表现出特征对称性，可通过沿1=0轴的“对称化数据”操作来去除杂峰，然而其代价是会降低某些信号的强度，同时可能会产生伪峰．如图2(a)所示的雌二醇的1D1H NMR谱图中，谱峰严重重叠．其2DRES谱[图2(b)]经过45˚谱图旋转和“对称化数据”操作，已将化学位移和偶合信息分解到两个正交维度．对于不拥挤区域的信号，如H2.52处谱峰，其化学位移和偶合信息都能得到很好地归属和测量．但对于H1.31～1.76的谱峰来说，其信号呈现出谱线展宽、分辨率下降的问题，无法正确获得所需要的信息．

图1 2DRESNMR实验的脉冲序列示意图

Fig. 1 Pulse sequence diagram of 2DRESNMR experiments

图2 500 MHz Varian谱仪所采集的雌二醇（溶于DMSO-6，浓度为200 mmol/L）的(a) 1D1H NMR谱和(b) 2DRES谱

Fig. 2 (a)1H NMR and (b) 2D-resolved spectra of 200 mmol/L estradiol (dissolved in DMSO-6) acquired on Varian spectrometer at 500 MHz

针对2DRES谱图相位扭曲的问题，可利用伪回波加权函数来直接抑制谱图信号中的色散成分，从而保留吸收线形信号[25]，但其代价是信号强度失真．也可以通过不需要傅里叶变换的方法来重建相敏2DRES谱图，例如正则求解变换[26,27]和滤波对角化[28,29]方法．另一种解决相位扭曲的常用方法是将型和型两种正交谱图相结合，从而获得相敏2DRES谱[30]．但2DRES实验的脉冲序列没有混频演化周期，单次实验不可能通过直接相位循环设计实现型和型谱的相干转移路径切换．现有的解决方法是在2DRES脉冲序列中引入-filter和片层选择（Zangger-Sterk，ZS）[31]等特殊的脉冲模块，并进行两次独立的实验，最终获得纯吸收模式的相敏2DRES谱，如Pell-Keeler方法[32]和梯度编码选择重聚（Gradient-encoded SElective ReFocusing，G-SERF）方法[33,34]．此外，通过引入PSYCHE（Pure Shift Yielded by CHirp Excitation）模块[35]来替代-filter或ZS模块的TSE (Triple Spin-Echo)-PSYCHE 2D[36]或PSYCHEDELIC（Pure Shift Yielded by CHirp Excitation to DELiver Individual Couplings）[37]，也能获得纯吸收模式的2DRES谱效果．相比于结合-filter和ZS的相敏2DRES谱，使用TSE-PSYCHE-2D和PSYCHEDELIC获得的2DRES谱具有更高的信噪比．但以上这些相敏RES谱仍需要通过45˚谱图旋转操作来实现化学位移和偶合信息的分离．作为TSE-PSYCHE 2D的扩展方法，-filter TSE-PSYCHE 2D[24]和PS(pure shift)-TSE-PSYCHE 2D[38]被用于获取正交模式相敏2DRES谱．这种谱图模式由Nagayama[39]首次提出，能够直接分离化学位移和偶合，避免45˚谱图旋转操作．然而，为了得到纯化学位移维度，需要增加一个额外的间接维，因此-filter TSE-PSYCHE 2D和PS-TSE-PSYCHE 2D这两种方法都不可避免地需要冗长的采样时间．上述所有相敏2DRES谱均是通过型和型两次正交谱图相结合实现的，这就要求两个独立实验的信号峰值强度必须保持一致，以保证色散成分完全消除，然而这一基本要求可能会增加实验操作的复杂性.

除了相位扭曲，强偶合伪峰也是RES谱存在的固有问题．强偶合伪峰是强偶合自旋体系在自旋回波模块（1/2-π-1/2）中π脉冲的混合作用下产生的．虽然强偶合效应并非RES谱想要获取的信息，但它通常与RES谱所期望获取的信号共享相干转移路径，因而不能通过常规的相位循环设计来消除．一种基于1周期演化模块设计的改进型2DRES谱技术可以用来抑制这些强偶合伪峰[40]，然而这一方法会增加采样时间．针对强偶合伪峰非对称多重结构，一种结合对称化处理的双自旋回波2DRES谱方法被提出用于减少这些强偶合伪峰[40]．由于一些对称的频率无法被移除，因而这一对称化处理方法往往不适用于复杂样品体系．此外，在实际2DRES谱应用中，采样效率也是需要考虑的另一重要因素[41-43]．与其他2D NMR实验相比，常规的2DRES谱间接维谱宽相对较窄，仅覆盖了裂分频率范围，在采样效率上具有一定优势．然而，在强偶合体系应用中，往往需要采样足够多的间接维演化点数来获得高分辨率的谱图，以保证强偶合裂分的精确测量，这就大幅延长了2DRES谱的采样时间．

针对常规2DRES谱中所遇到问题，为满足2DRES谱应用于复杂样品体系的需求，我们小组基于纯化学位移演化模块和回波链采样模块，提出了正交相敏2DRES谱方法，包括RASA2D（Rapid Absorption-mode and Strong-coupling Artifact-reduction 2D-resolved spectroscopy）、OPAM-2D（Orthogonal-Pattern Absorption-Mode 2D-resolved spectroscopy）和HR-G-SERF（High-Resolution Gradient-encoded SElective ReFocusing）/AH-G-SERF（Accelerated High-resolution Gradient-encoded SElective ReFocusing）.下文我们对这三种正交相敏2DRES谱方法进行回顾，重点阐述其方法原理和应用特性．

1 基于PSYCHE的正交相敏2D JRES方法—RASA2DJ

RASA2D是一种在高采样效率前提下，能克服强偶合的正交相敏2DRES谱方法[44]，其脉冲序列如图3所示．该脉冲序列融合了PSYCHE纯化学位移模块和回波链采样模块，即将一维PSYCHE序列的采样部分替换成回波链采样模块，从而得到正交2DRES谱，不需要45˚谱图旋转操作，即可直接将偶合和化学位移信息分解在两个正交的维度，相当于每个谱峰的化学位移点在其相应垂直方向上添加了相应的偶合裂分信息．此外，还可通过在第一个非选择性π/2脉冲前添加一个预饱和压水（Presat）模块来实现一些实际应用所需的压水操作．这里的PSYCHE模块包含了一个非选择性π/2激发脉冲、一个被二等分的间接演化周期1、一个具有相干选择梯度的非选择性π/2脉冲和一对具有相干选择梯度且匹配弱梯度的扫频Chirp脉冲．回波序列采样模块由直接采样周期2和π脉冲组成，包含奇数和偶数采样部分，并重复次．RASA2D数据采样完后，需要经过后续数据重构和相应相敏处理来最终得到相敏2DRES谱图．在数据重构过程中，通常只用RASA2D数据的奇数回波采样部分，先经过数据拼接得到直接维纯化学位移数据，接着按照22间接维演化时间间隔，对拼接后的一维纯化学位移数据进行排序，最终重构得到2DRES谱数据．这一重构二维数据直接经过二维傅里叶变换即可得到正交2DRES谱，即直接维包含纯化学位移信息，而间接维包含偶合信息．但这个二维谱信号在两个不同维度上均受到相位扭曲的影响，我们设计了特定数据相敏处理操作来获得最终的相敏2DRES谱，具体流程如图3(b)所示．首先，傅里叶变换后的原始正交2DRES谱经过1¢维反转操作，并与原有谱图进行相加，可直接消除1¢维信号相位扭曲，即消除信号色散部分而保留吸收信号部分；接着，沿着2¢维进行相应相位校正，得到纯吸收线形显示的相敏2DRES谱.

图3 基于PSYCHE的正交相敏2DRES谱—RASA2D. (a) 脉冲序列，由1D PSYCHE和回波链采样模块组成．在第一个非选择性π/2脉冲之前适用了一个预饱和（Presat）模块进行水峰抑制．长条形脉冲分别代表π/2和π脉冲，两个带有斜箭头的半圆形代表小翻转角（<< π/2）的扫频方向相反的脉冲，1和2是相干选择梯度，3是与扫频脉冲配合使用的弱梯度，1是间接维演化时间，2是直接维采样时间，SW1是1对应的谱宽，是相邻两个π脉冲之间的间隔．(b)以二维相敏谱中的单峰信号为例展示数据相敏处理流程，包括关于1¢=0轴翻转原始谱图后，将其与原始谱图相加，并将相加后的谱图沿2¢维进行一维相位校正可得相敏结果（摘自文献[44]）

Fig. 3 PSYCHE based orthogonal-pattern phase-sensitive-resolved spectroscopy, RASA2D. (a) Pulse sequence diagram constituted of 1D PSYCHE and echo-trainacquisition module. A presaturation (Presat) module is adopted before the first nonselective π/2 pulse for water suppression. Vertical bars indicate nonselective π/2 and π pulses, two semicircle shaped pulses with diagonal arrows are frequency-swept chirp pulses with small flip angle≪ π/2,1and2are coherence selection gradients,3is a weak gradient matching with chirp pulses,1is the indirect evolution period and2is the direct acquisition period, SW1 is the spectral width corresponding to1, andis the time interval between two adjacent π pulses. (b) The procedure of phase-sensitive processing is illustrated using a singlet peak in a 2D phase-sensitive spectrum, including preserving an original spectrum and generating an1¢-reversed spectrum, summing these two spectra, and performing 1D phase correction along the2¢dimension (Excerpted from Ref. [44])

图4所示为RASA2D方法应用于具有小偶合常数体系和复杂样品体系的实验结果[44]．使用RASA2D所得到2DRES谱图中，所有谱峰信号均显示为吸收线形模式，相比于传统2DRES谱的绝对值显示模式，谱图分辨率提高了2倍．由于采用回波链采样模式，即在回波链采样过程实现偶合演化，RASA2D只需要单次实验就可以记录完整偶合演化过程，不需要通过相位循环设计实现型和型谱的相干转移路径切换，避免了冗长间接维点数的递进演化．因此RASA2D可在偶合维度上实现非常高的分辨率，特别有利于小偶合常数的测量．如图4左侧所示，利用RASA2D得到的2DRES谱可以测量在常规1D NMR谱无法获得的偶合常数0.5 Hz和0.8 Hz，其实验参数设置如下：非选择性π/2脉冲宽度为12.8 μs；每个Chirp脉冲长度为15 ms；扫频宽度为10 kHz；翻转角度为12˚；相干选择梯度1和2的强度分别为0.20 T/m和0.32 T/m，持续时间为1.5 ms；弱梯度3的强度为0.009 T/m；采样时间2为11.1 ms；回波链采样模块的重复次数为80，重建的偶合维度的谱宽为45 Hz（1/(22)）；间接维谱宽SW1和SW2分别为90 Hz和9 kHz；脉冲重复时间为2.0 s；1增量的数量和实验累加次数分别为60和2．RASA2D应用于复杂样品体系时也独具优势，如图4右侧所示，RASA2D方法用于高分辨检测复杂的雌二醇样品时，在直接维显示了相敏纯化学位移谱，在间接维垂直正交显示与分子结构解析相关的偶合裂分信息．与前一实验不同的参数设置如下：采样时间2为10 ms；回波链采样模块的重复次数为50，重建的偶合维度的谱宽为50 Hz；间接维谱宽SW1和SW2分别设为100 Hz和10 kHz；脉冲重复时间为1.5 s；1增量的数量和实验累加次数分别设为50和4.

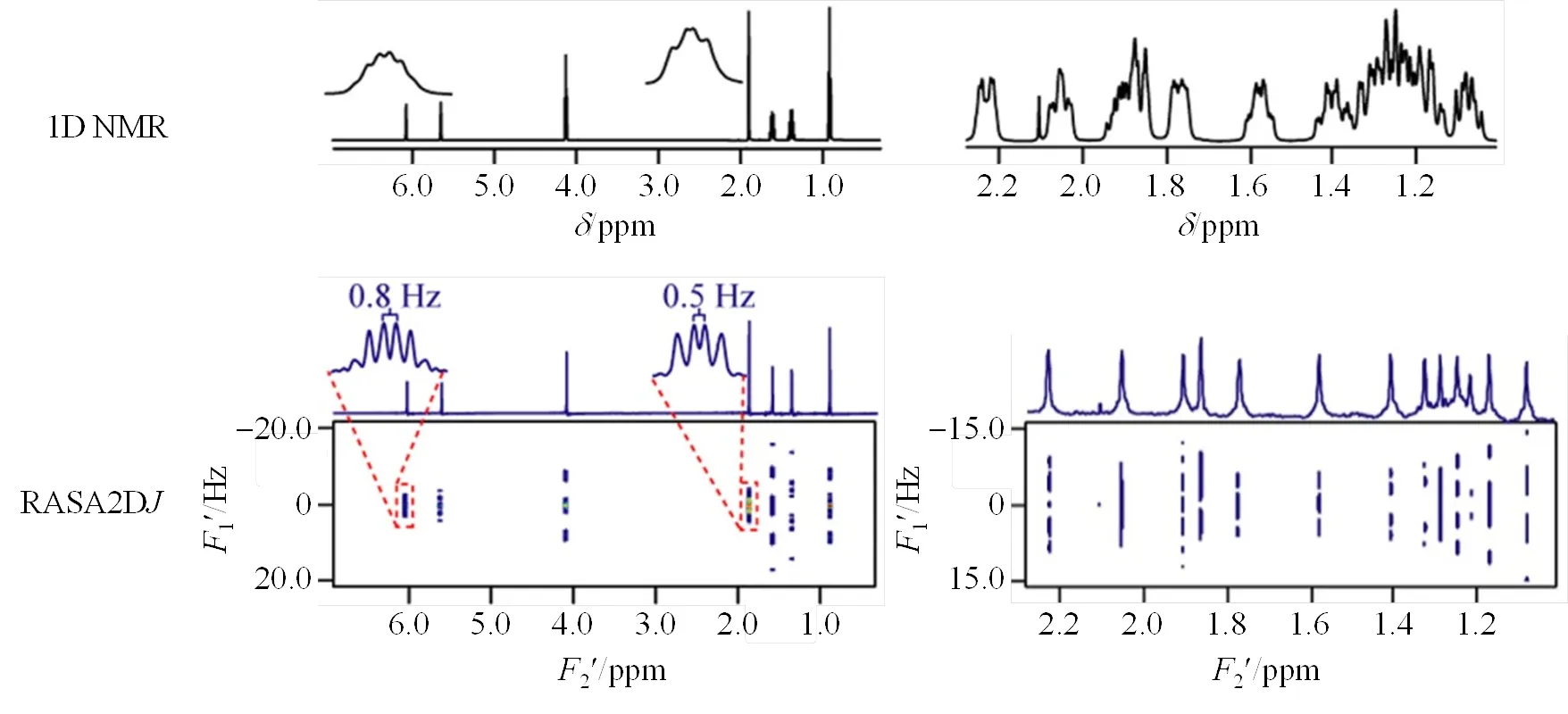
图4 RASA2DJ方法应用于具有小J偶合常数体系和复杂样品体系．左侧为溶于DMSO-d6的甲基丙烯酸丁酯的1D NMR谱和RASA2DJ谱，RASA2DJ的总采样时间为4 min；右侧为溶于DMSO-d6的雌二醇（部分区域）的1D NMR谱和RASA2DJ谱，RASA2DJ的总采样时间为5 min（根据文献[44]修改）

2 基于ZS的正交相敏2D JRES方法—OPAM-2DJ

基于PSYCHE的正交相敏2DRES方法通常仅适用于均匀磁场环境．然而，NMR实际应用于非均相生物组织和原位电化学体系时，磁场不均匀性往往很难避免，这就导致2DRES谱的谱峰沿化学位移维度不均匀展宽，给化学位移和偶合信息的测量带来挑战．为消除这种不均匀谱线展宽效应，一系列基于自旋回波相关（spin-echo correlation，SECSY）模块[45]和分子间多量子相干演化（intermolecular multiple-quantum coherence，iMQCs）[46]的高分辨2DRES方法相继被提出．虽然这些高分辨方法能应用于不均匀磁场，但它们通常仍无法获得相敏模式的2DRES谱图．

基于ZS纯化学演化模块与回波链采样模块，我们提出了一种称为OPAM-2D[47]的改进2DRES方法，可用于不均匀磁场环境下正交相敏2DRES谱的采集，其脉冲序列如图5所示．图5(a)是单层激发版本的OPAM-2D序列；图5(b)是多层激发版本的OPAM-2D序列，使用傅里叶相位编码方法进行多层信号解码．与RASA2D方法不同的是，OPAM-2D方法将一对扫频Chirp脉冲换成了一个选择性π脉冲，由选择性π脉冲和弱梯度结合使用的模块实现片层选择．最终，谱图上的每个信号都来源于一个与位置相关的特定小体素片层，这是OPAM-2D能够克服不均匀场的原因之一．另一个原因是这一方法使用了回波链采样模块，这一模块能够重聚在采样期间的磁场不均匀效应，减少了不均匀磁场对谱图的影响．图6为使用常规2DRES方法与OPAM-2D方法在不均匀磁场环境下获得的25 mmol/L溶于DMSO-6的阿奇霉素样品的谱图对比[47]．由图6(a)可以看出，由于磁场不均匀效应导致谱线大幅增宽，使用常规2DRES方法获得的谱图几乎无法提供有用的信息．而使用单层激发OPAM-2D方法在不均匀场下采集的2DRES谱[图6(b)]以正交相敏模式显示，在直接维可获得纯化学位移谱峰信息，而间接维给出偶合信息，该实验参数设置如下：相干选择梯度1、2和3的强度为11 G/cm（1 G/cm=10-4T/cm）、11 G/cm和-22 G/cm，持续时间为1.0 ms；弱梯度z的强度为0.37 G/cm；相干选择梯度4的强度为0 G/cm；单色π脉冲宽度为13.9 ms；1增量的数量为40；单个回波链采样模块的采样时间为10.25 ms；回波链采样模块的重复次数为50；直接维谱宽SW和间接维谱宽SW1分别设为10 kHz和100 Hz.

图5 (a)单层激发和(b)多层激发的OPAM-2D实验的脉冲序列示意图．该序列由纯化学位移ZS模块和回波链采样模块组成．绿色填充代表π/2和π非选择性脉冲；红色填充代表单色π脉冲；黄色填充代表多色π/2和π脉冲；z为与空间选层脉冲相匹配的弱梯度；1、2、3和4是相干选择路径梯度；m,n为附加的傅里叶编码相位；序列的相位为：1(, −)、2()、3(,,,,-,-,-,-)、rec(,,,)；4在回波链采样模块中，遵循(,,-,-)的相位（摘自文献[47]）

Fig. 5 Pulse sequences for (a) single-band and (b) multi-band OPAM-2Dexperiments. The sequence is constituted of ZS and echo-trainacquisition modules. Green bars denote π/2 and π nonselective pulses, respectively. The red-shaped pulse represents monochromatic π pulse. The yellow-shaped pulses represent polychromatic π/2 and π pulses.zindicates the weak gradient for extracting spatial slice-selective signals;1,2,3,4are used for coherence pathway selection.m,nis the appended Fourier encoding phase. Phase cycling:1(, −),2(),3(,,,, −, −, −, −),rec(,,,).4is varied as (,, −, −) in the echo-trainacquisition module (Excerpted from Ref. [47])

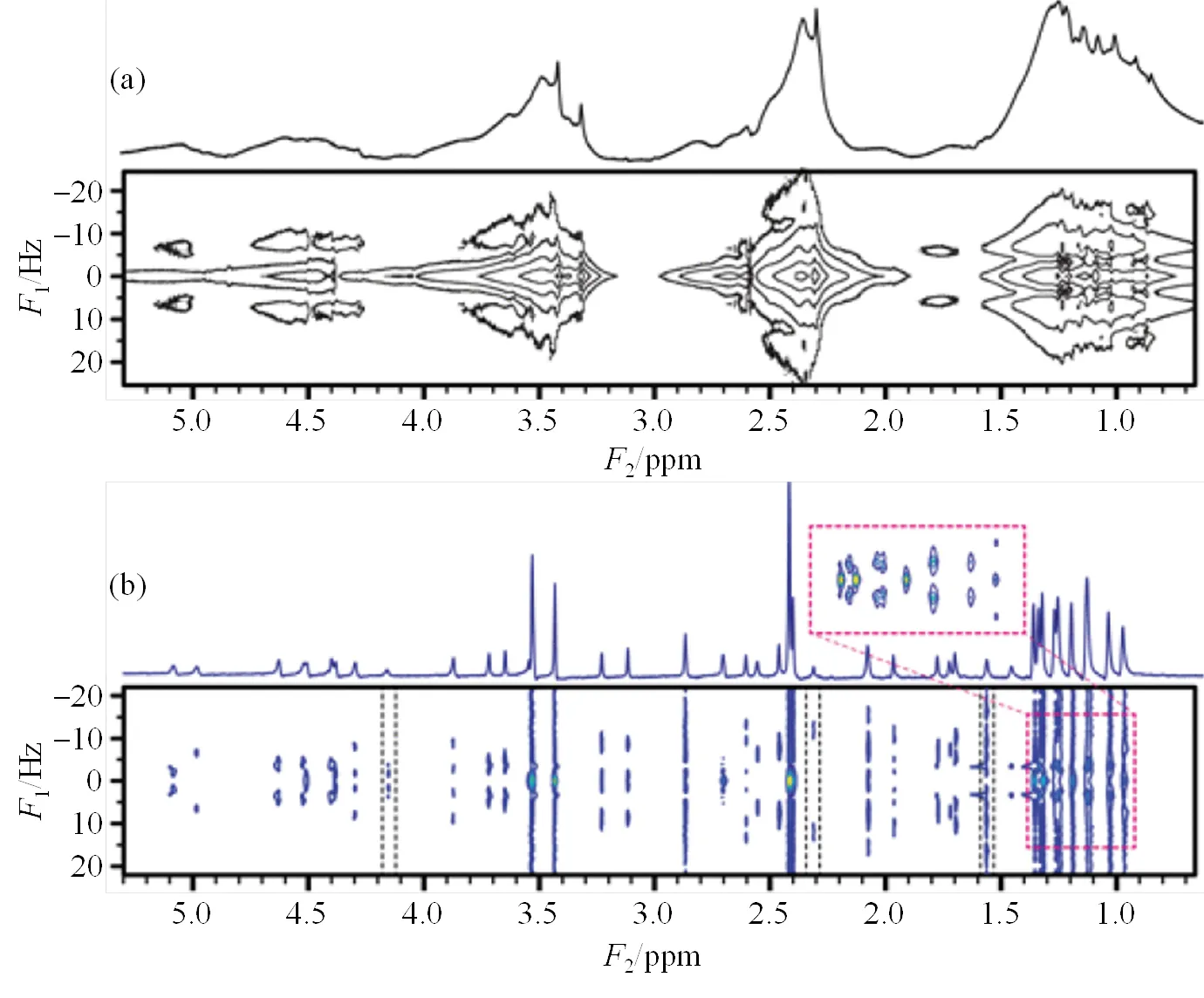
图6 在不均匀磁场环境下获得的(a)常规2D JRES谱和(b)单层激发OPAM-2DJ谱（根据文献[47]修改）

OPAM-2D方法能够记录正交模式2DRES谱，纯化学位移和偶合信息分别在正交维上呈现，避免了45˚谱图旋转．在采样效率方面，亦能够在几分钟内实现快速2D采样．同时，得到的OPAM-2D谱图可以相敏模式显示，减少的强偶合伪峰带来的影响．相比于RASA2D方法，OPAM-2D还能克服沿方向的主磁场的不均匀性，从而实现非理想磁场条件下复杂样品体系偶合信息测量与多重结构的分析，使获得具有固有磁化率变化的生物组织的检测分析成为可能.

3 应用于非均匀磁场下高分辨2D J-编辑谱方法

2DRES谱可用于提取和识别重叠区域每个质子的多重偶合信息，无需预先获知质子准确化学位移信息就能实现其偶合常数的测量．然而这一方法只能获得特定质子的所有偶合信息．为了提取特定相互作用下单个偶合信息，Berger等[48]提出了双重选择重聚（SElective ReFocusing，SERF）方法，每次实验所提取的偶合信息仅限于所选择的两个自旋偶合质子之间．若要得到全部的偶合网络信息，需要重复多次实验，采样效率相对较低．此后，G-SERF[49]被提出来用于在一次实验中得到与选定质子偶合相关的所有偶合信息，大幅度提升了实验效率．Clean-G-SERF[50]是G-SERF的改进版本，可用于消除轴峰和不需要的偶合信号，简化偶合网络信息表达．此外，SECT（SElective Constant-Time）[51,52]方法也可以在高信噪比的情况下显示出理想的偶合信息．目前，这些SERF方法应用于复杂样品体系时，能起到简化谱峰信息、实现特定偶合网络编辑谱功能的作用．除谱峰拥挤外，空间磁场非均匀变化也是降低2D编辑谱谱图分辨率、阻碍其应用的另一因素．在液态均相样品实验中，可通过匀场技术来使外部磁场达到均匀状态．然而，在非均相半固态样品应用测量时，例如具有固有磁化率变化的生物组织等，普遍存在难以消除的磁场不均匀性，即使对于均匀样品，轻微的磁场扰动也能导致谱图信息模糊，干扰特征谱峰信息识别，尤其是对于复杂样品体系．理论上，基于G-SERF模块的方法可以解决沿梯度编码方向（通常为轴）的磁场空间非均匀变化问题．然而，这些方法在不利磁场条件下的应用都还尚未得到深入研究．

基于此，我们小组提出了可应用于不均匀磁场环境下获得高分辨2D-编辑谱的方法，包括基于3D采样的HR-G-SERF方法和基于2D快速采样的AH-G-SERF方法，同时解决2D-编辑谱应用中存在的谱峰拥挤和由磁场不均匀性导致的谱图分辨率下降的问题，而且最终得到的谱图以正交相敏显示，避免常规2D编辑谱所需的45˚谱图旋转操作[53]．图7(a)为HR-G-SERF脉冲序列，其信号演化随1增量的变化仅受到所选质子与其偶合核之间的偶合调制作用，从而在1维上揭示了偶合网络关系．在2维中，纯化学位移随变量2演化消除偶合作用．最终在两个正交维度（1和2）上得到其偶合信息和纯化学位移信息．再将谱图进行相应相敏处理，即关于1=0轴对称后与原谱图相加，即可得到相敏2D-编辑谱．该序列中使用了ZS模块，能实现小体素片选信号的积分，因而能在一定程度上抑制磁场不均匀性对谱图的干扰．图7(b)为AH-G-SERF脉冲序列，由ZS模块和G-SERF回波链模块组成．通过使用回波链，AH-G-SERF将2D-编辑谱实验中3D采样压缩为2D采样，进一步提高了采样效率．

上述两种高分辨2D-编辑谱方法可以在一次实验中确定与选定质子相关的整个偶合网络；同时能够将纯吸收模式2D编辑谱变换成正交模式，让纯化学位移沿直接维分布，而偶合信息沿正交间接维分布，便于在拥挤NMR谱中进行偶合网络信息测量；而且，能够克服方向磁场不均匀性，可用于非均匀相样品体系，如生物组织的高分辨检测[46,54-56]．图8为使用HR-G-SERF方法在均匀和非均匀磁场条件下获得的250 mmol/L溶于DMSO-6的雌二醇样品的-编辑谱[53]．结果显示，在均匀场和不均匀场下，复杂样品的偶合常数都能够得到精确测量，相应的偶合网络关系也能够得到正确归属．在3D HR-G-SERF实验[对应图8(c)、8(d)、8(f)、8(g)的实验]中，实验参数设置如下：相干选择梯度1、2的强度为3.7 G/cm、7.3 G/cm，持续时间为0.5 ms；弱梯度z的强度为0.37 G/cm；直接维谱宽SW为5 000 Hz，采样点数为3 968；对应偶合演化的间接维谱宽SW1设为20 Hz，1增量的数量设为40；对应纯化学位移演化的间接维谱宽SW2设为50 Hz，2增量的数量设为25．用于重聚激发H-9及H-15的选择性脉冲宽度设为25 ms，与弱梯度z一起的选择性脉冲宽度设为25 ms；扫描间延迟时间1设为1s；空扫次数设为16；实验累加次数设为8；总实验时间约为4 h 30 min．在仅递增1的HR-G-SERF实验中，与3D HR-G-SERF实验不同的实验参数设置如下：直接维谱宽SW设为10 000 Hz，采样点数为20 000；对应偶合演化的间接维谱宽SW1设为20 Hz，1增量的数量设为30，总实验时间为6 min．

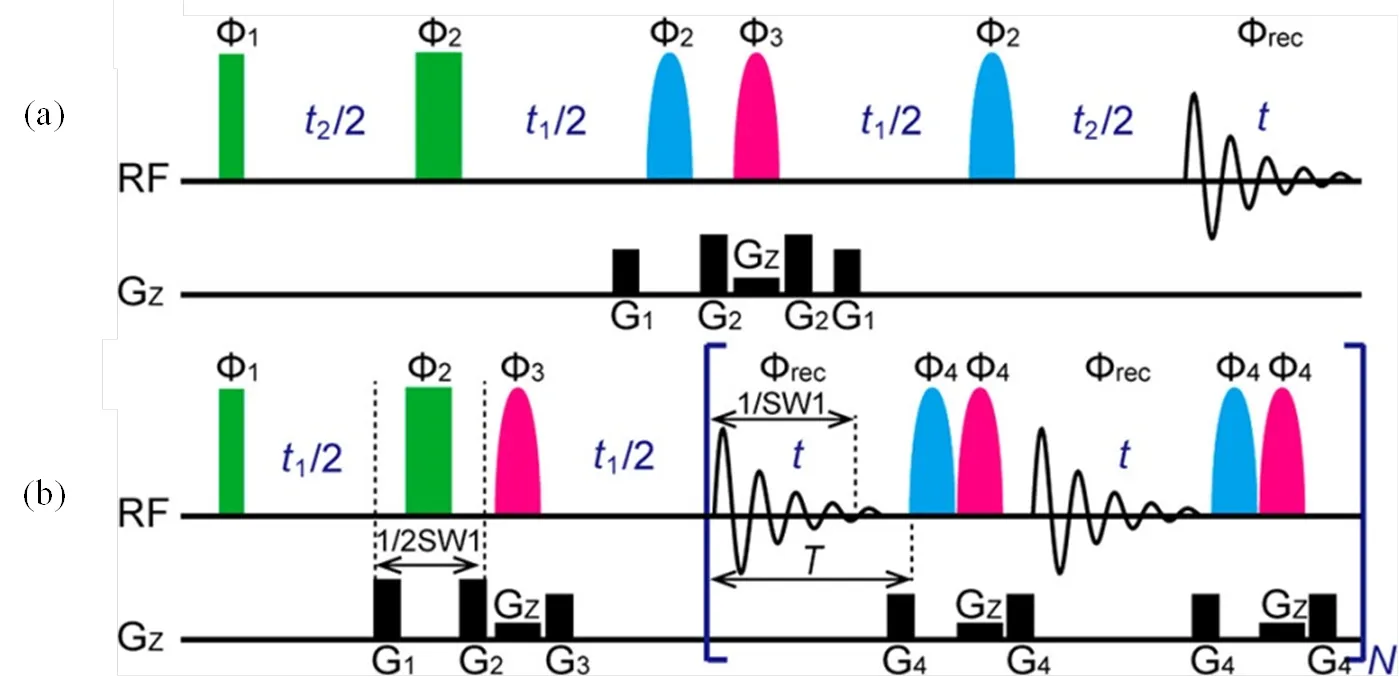
图7 应用于不均匀磁场下的高分辨2D J-编辑谱方法. (a)基于3D采样的HR-G-SERF实验序列，相位循环：Φ1 (x, −x), Φ2 (x), Φ3 (x, x, y, y, −x, −x, −y, −y), Φrec (x, −x, −x, x). (b)基于2D快速采样的AH-G-SERF实验序列，由ZS模块和G-SERF回波链模块组成设计的，相位循环：Φ1=Φ2=Φ3=Φrec=x，Φ4在J编辑回波链采样模块中以(x, x, x, x, -x, -x, -x, -x)N/2为循环．细绿色长条和粗绿色长条分别表示π/2和π非选择性脉冲，蓝色和红色填充形状表示的分别是用于选择特定质子和空间编码的π选择性脉冲；Gz为空间编码的弱梯度，G1、G2、G3和G4为相干选择梯度（摘自文献[53]）

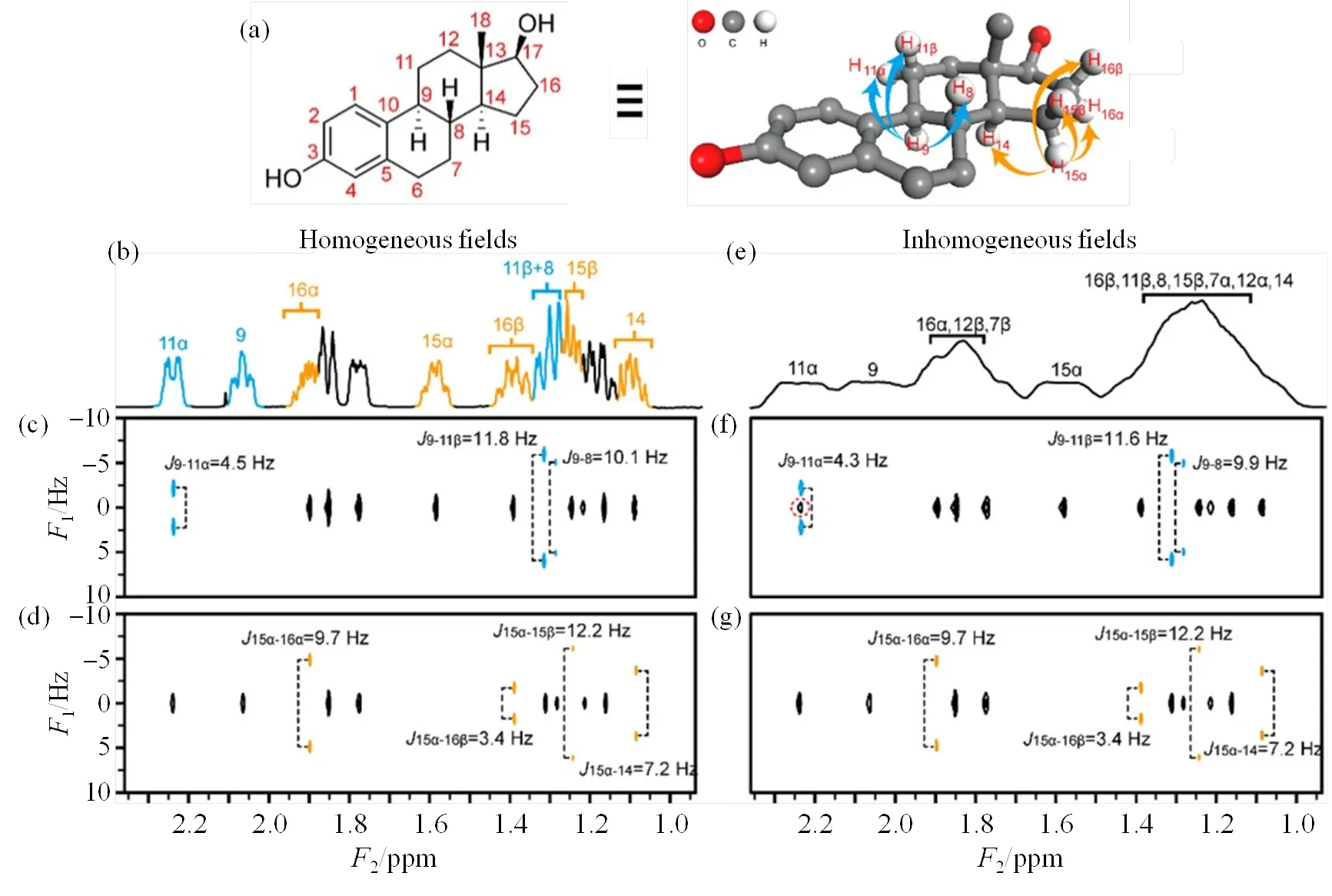
图8 不同磁场环境下，使用HR-G-SERF方法获得的雌二醇样品的高分辨2D J-编辑谱. (a)分子结构信息和所观察的偶合网络；(b～d)均匀磁场下的1D NMR谱、激发H-9及H-15a的2D J-编辑谱；(e～g)不均匀磁场下的1D NMR谱、激发H-9及H-15a的2D J-编辑谱（根据文献[53]修改）

4 总结与展望

2DRES谱可通过分离化学位移和偶合信息，从而解决1D1H NMR谱应用于复杂体系时遇到的谱峰拥挤问题．本文首先回顾了一系列相关的2DRES谱方法，然后针对传统2DRES谱方法遇到的困境，详细介绍了三种基于纯化学位移的正交相敏2DRES谱的原理和应用．相比于常规2DRES谱，正交相敏2DRES谱方法表现出如下优势：一方面能够避免45˚谱图旋转操作；另一方面谱图以相敏模式显示，提高谱图分辨率；同时，这些方法也能一定程度上避免强偶合伪峰的产生；并且，可应用于非均匀磁场环境．相关实验也证明了正交相敏2DRES方法可用于生物组织和复杂样品体系，以及强偶合体系的偶合信息的准确测量．

但由于纯化学位移信号演化本身固有的信号强度低的缺点，上述正交相敏2DRES谱也不可避免地存在信噪比损失的问题．如何在不降低采样效率的前提下，提高谱图的灵敏度，将成为扩展其应用范围的关键．另外，数据拼接过程中存在着调制残留，使得谱图中也会有伪峰的存在，如何去除正交相敏2DRES谱中的伪峰，也值得研究．对于回波链来说，由于只使用了奇数段，所采样数据只有50%左右的使用率，对于弛豫时间很短的样品来说，这一方法的使用会受到一定程度限制．以上这些缺陷都可通过优化设计脉冲序列，或结合有效的数据后处理方法来进一步解决．

无

[1] DI CARO D, LIGUORI C, PIETROSANTO A, et al. Quality assessment of the inshell hazelnuts based on TD-NMR analysis[J]. IEEE Trans Instrum Meas, 2020, 69(6): 3770-3779.

[2] EVANGELIDIS T, NERLI S, NOVACEK J, et al. Automated NMR resonance assignments and structure determination using a minimal set of 4D spectra[J]. Nature Commun, 2018, 9(1): 1-13.

[3] TOYAMA Y, KANO H, MASE Y, et al. Dynamic regulation of GDP binding to g proteins revealed by magnetic field-dependent NMR relaxation analyses[J]. Nature Commun, 2017, 8(1): 1-15.

[4] HUANG Y Q, ZHAN H L, YOU X Q, et al. A pure shift-based NMR method for transverse relaxation measurements on complex samples[J]. IEEE Trans Instrum Meas, 2020, 69(1): 201-211.

[5] DU G F, LIN J, ZHANG J, et al. Study on shortening the dead time of surface nuclear magnetic resonance instrument using bipolar phase pulses[J]. IEEE Trans Instrum Meas, 2020, 69(4): 1268-1274.

[6] FU R Q, MIAO Y M, QIN H J, et al. Probing hydronium ion histidine NH exchange rate constants in the m2 channel via indirect observation of dipolar-dephased15N signals in magic-angle-spinning NMR[J]. J Amer Chem Soc, 2016, 138(49): 15801-15804.

[7] FRYDMAN L, SCHERF T, LUPULESCU A. The acquisition of multidimensional NMR spectra within a single scan[J]. Proc Nat Acad Sci USA, 2020, 99(25): 15858-15862.

[8] CHEN X L, LV W, SU Q C. Conversion of lignocellulose studied by nuclear magnetic resonance[J]. Chinese J Magn Reson, 2021, 38(2): 277-290.

陈晓丽, 吕微, 苏秋成, 等. 核磁共振技术在生物质转化中的应用[J]. 波谱学杂志, 2021, 38(2): 277-290.

[9] ZANGGER K. Pure shift NMR[J]. Prog Nucl Magn Reson Spectrosc, 2015, 86-87: 1-20.

[10] ZHOU Q J, XIANG J F, TANG Y L, et al. Pure shift proton NMR spectroscopy and its application[J]. Chinese J Magn Reson, 2016, 33(3): 502-513.

周秋菊, 向俊峰, 唐亚林, 等. 纯位移核磁共振氢谱及其应用[J]. 波谱学杂志, 2016, 33(3): 502-513.

[11] LIN X Q, LI H, ZHAN H L, et al. High-resolution pure shift NMR spectroscopy and its applications[J]. Chinese J Magn Reson, 2019, 36(4): 425-436.

林晓晴, 李弘, 詹昊霖, 等. 高分辨率核磁共振纯化学位移谱新方法及其应用[J]. 波谱学杂志, 2019, 36(4): 425-436.

[12] HUNG I, GAN Z H. High-resolution NMR of=3/2 quadrupole nuclei by detection of double-quantum satellite transitions via protons[J]. J Phys Chem Lett, 2020, 11(12): 4734-4740.

[13] BIFULCO G, DAMBRUOSO P, GOMEZ-PALOMA L, et al. Determination of relative configuration in organic compounds by NMR spectroscopy and computational methods[J]. Chem Rev, 2007, 107(9): 3744-3779.

[14] THOMAS W A. Unravelling molecular structure and conformation-the modern role of coupling constants[J]. Prog Nucl Magn Reson Spectrosc, 1997, 30: 183-207.

[15] REIF B, HENNIG M, GRIESINGER C. Direct measurement of angles between bond vectors in high-resolution NMR[J]. Science, 1997, 276(5316): 1230-1233.

[16] LI Y J, YANG H J, LIU J H, et al. Assignments of NMR spectral data of a novel carbazole-triazinoindole based-acylhydrazone derivative[J]. Chinese J Magn Reson, 2020, 37(4): 496-504.

李英俊, 杨鸿境, 刘季红, 等. 基于咔唑-三嗪并吲哚的-酰腙衍生物的NMR数据归属[J]. 波谱学杂志, 2020, 37(4): 496-504.

[17] AUE W P, KARHAN J, ERNST R R. Homonuclear broad band decoupling and two-dimensional-resolved NMR spectroscopy[J]. J Chem Phys, 1976, 64: 4226-4227.

[18] KIKUCHI J, TSUBOI Y, KOMATSU K, et al. Spin couple: development of a web tool for analyzing metabolite mixtures via two-dimensional-resolved NMR database[J]. Anal Chem, 2016, 88(1): 659-665.

[19] LUPULESCU A, AHARON H, FRYDMAN L. Two-dimensional RF pulses: A new approach to selectively exciting-coupled spins in nuclear magnetic resonance[J]. J Chem Phys, 2013, 139(14): 144204.

[20] ESPINDOLA A P D M, CROUCH R, DEBERGH J R, et al. Deconvolution of complex NMR spectra in small molecules by multi frequency homonuclear decoupling (MDEC)[J]. J Amer Chem Soc, 2009, 131(44): 15994-15995.

[21] YILMAZ A, NYBERG N T, JAROSZEWSKI J W. Metabolic profiling based on two-dimensional-resolved1H NMR data and parallel factor analysis[J]. Anal Chem, 2011, 83(21): 8278-8285.

[22] LUDWIG C, VIANT M R. Two-dimensional-resolved NMR spectroscopy: review of a key methodology in the metabolomics toolbox[J]. Phytochem Anal, 2010, 21(1): 22-32.

[23] RACHINENI K, KAKITA V M R, DAYAKA S, et al. Precise determination of enantiomeric excess by a sensitivity enhanced two-dimensional band-selective pure-shift NMR[J]. Anal Chem, 2015, 87(14): 7258-7266.

[24] KIRALY P, FOROOZANDEH M, NILSSON M, et al. Anatomising proton NMR spectra with pure shift 2D-spectroscopy: A cautionary tale[J]. Chem Phys Lett, 2017, 683: 398-403.

[25] BAX A, FREEMAN R, MORRIS G A. A simple method for suppressing dispersion-mode contributions in NMR spectra: The “pseudo echo”[J]. J Magn Reson, 1981, 43(2): 333-338.

[26] ARMSTRONG G S, CHEN J H, CANO K E, et al. Regularized resolvent transform for direct calculation of 45° projections of 2Dspectra[J]. J Magn Reson, 2003, 164(1): 136-144.

[27] CHEN J H, SHAKA A J, MANDELSHTAM V A. RRT: The regularized resolvent transform for high-resolution spectral estimation[J]. J Magn Reson, 2000, 147(1): 129-137.

[28] MANDELSHTAM V A, TAYLOR H S, SHAKA A J. Application of the filter diagonalization method to one- and two-dimensional NMR spectra[J]. J Magn Reson, 1998, 133(2): 304-312.

[29] HU H T, DE ANGELIS A A, MANDELSHTAM V A, et al. The multidimensional filter diagonalization method - II. Application to 2D projections of 2D, 3D, and 4D NMR experiments[J]. J Magn Reson, 2000, 144(2): 357-366.

[30] KEELER J, NEUHAUS D. Comparison and evaluation of methods for two-dimensional NMR spectra with absorption-mode lineshapes[J]. J Magn Reson, 1985, 63(3): 454-472.

[31] ZANGGER K, STERK H. Homonuclear broadband-decoupled NMR spectra[J]. J Magn Reson, 1997, 124(2): 486-489.

[32] PELL A J, KEELER J. Two-dimensional-spectra with absorption-mode lineshapes[J]. J Magn Reson, 2007, 189(2): 293-299.

[33] MISHRA S K, LOKESH N, SURYAPRAKASH N. Clean G-SERF an NMR experiment for the complete eradication of axial peaks and undesired couplings from the complex spectrum[J]. RSC Adv, 2017, 7(2): 735-741.

[34] LOKESH N, CHAUDHARI S R, SURYAPRAKASH N. Quick re-introduction of selective scalar interactions in a pure-shift NMR spectrum[J]. Chem Commun, 2014, 50(98): 15597-15600.

[35] FOROOZANDEH M, ADAMS R W, MEHARRY N J, et al. Ultrahigh-resolution NMR spectroscopy[J]. Angew Chem Int Ed, 2014, 53(27): 6990-6992.

[36] FOROOZANDEH M, ADAMS R W, KIRALY P, et al. Measuring couplings in crowded NMR spectra: pure shift NMR with multiplet analysis[J]. Chem Commun, 2015, 51(84): 15410-15413.

[37] SINNAEVE D, FOROOZANDEH M, NILSSON M, et al. A general method for extracting individual coupling constants from crowded1H NMR spectra [J]. Angew Chem Int Ed, 2016, 55(3): 1090-1093.

[38] SINNAEVE D. Clean pure shift 2D-resolved spectroscopy[J]. Magn Reson Chem, 2018, 56(10): 947–953.

[39] NAGAYAMA K. Spin decoupling in two-dimensional-resolved NMR spectroscopy[J]. J Chem Phys, 1979, 71: 4404–4415.

[40] THRIPPLETON M J. EDDEN R A E, KEELER J. Suppression of strong coupling artefacts in-spectra[J]. J Magn Reson, 2005, 174(1): 97-109.

[41] GAL M, MISHKOVSKY M, FRYDMAN L. Real-time monitoring of chemical transformations by ultrafast 2D NMR spectroscopy[J]. J Amer Chem Soc, 2006,128(3): 951-956.

[42] VIANT M R. Improved methods for the acquisition and interpretation of NMR metabolomic data[J]. Biochem Biophys Res Commun, 2003, 310(3): 943-948.

[43] TAL A, FRYDMAN L. Single-scan multidimensional magnetic resonance[J]. Prog Nucl Magn Reson Spectrosc, 2010, 57(3): 241-292.

[44] HUANG Y Q, YANG Y, CAI S H. General two-dimensional absorption-mode‑resolved NMR spectroscopy[J]. Anal Chem, 2017, 89(23): 12646-12651.

[45] PELUPESSY P, RENNELLA E, BODENHAUSEN G. High-resolution NMR in magnetic fields with unknown spatiotemporal variations[J]. Science, 2009, 324(5935): 1693-1697.

[46] FUGARIU I, BERMEL W, LANE D, et al. In-phase ultra high-resolution inNMR[J]. Angew Chem Int Ed, 2017, 56(22): 6324-6328.

[47] ZHAN H L, HUANG Y Q, CHEN Z. An orthogonal-pattern absorption-mode 2D-resolved NMR spectroscopy for analyses on complex samples[J]. IEEE Trans Instrum Meas, 2021, 70:6004509.

[48] FACKE T, BERGER S. SERF, a new method for H, H spin-coupling measurement in organic chemistry[J]. J Magn Reson Ser A, 1995, 113(1): 114-116.

[49] GIRAUD N, BEGUIN L, COURTIEU J, et al. Nuclear magnetic resonance using a spatial frequency encoding: application to-edited spectroscopy along the sample[J]. Angew Chem Int Ed, 2010, 49(20): 3481-3484.

[50] MISHRA S K, LOKESH N, SURYAPRAKASH N. Clean G-SERF an NMR experiment for the complete eradication of axial peaks and undesired couplings from the complex spectrum[J]. RSC Adv, 2017, 7(2): 735-741.

[51] LIN L J, WEI Z L, LIN Y Q, et al. MeasuringHHvalues with a selective constant-time 2D NMR protocol[J]. J Magn Reson, 2016, 272: 20-24.

[52] CHEN J Y, ZENG Q, LIN Y Q, et al. Simultaneous multi-slice selective constant-time-resolved spectroscopy for measuringvalues[J]. Chinese J Magn Reson, 2019, 36(4): 456-462.

陈金永, 曾庆, 林雁勤, 等. 用于测量偶合常数的同时多层选择性恒时分解谱的方法[J]. 波谱学杂志, 2019, 36(4): 456-462.

[53] ZHAN H L, HUANG Y Q, WANG X C, et al. Highly efficient determination of complex NMR multiplet structures in inhomogeneous magnetic fields[J]. Anal Chem, 2021, 93: 2419-2423.

[54] PELUPESSY P, RENNELLA E, BODENHAUSEN G. High-resolution NMR in magnetic fields with unknown spatiotemporal variations[J]. Science, 2009, 324(5935): 1693-1697.

[55] GAN Z H, HUNG I, WANG X L, et al. NMR spectroscopy up to 35.2 T using a series-connected hybrid magnet[J]. J Magn Reson, 2017, 284: 125-136.

[56] LAMBERT J, HERGENRODER R, SUTER D, et al. Probing liquid-liquid interfaces with spatially resolved NMR spectroscopy[J]. Angew Chem Int Ed, 2009, 48 (34): 6343-6345.

Two-Dimensional Homonuclear Orthogonal-Pattern Phase-Sensitive-Resolved NMR Spectroscopy Based on Pure Shifts

，，，，CHEN Zhong

Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China

Two-dimensional-resolved (2DRES) nuclear magnetic resonance (NMR) experiments provide a simple and user-friendly spectral representation, in whichcouplings and chemical shifts are separated into two orthogonal frequency dimensions. The 2DRESexperiments have attracted wide attention in fundamental pulse sequence developments and practical applications, since they were first proposed 40 years ago. In this paper, we review the recent advances in the development of novel 2DRESpulse sequences and 2D-edited methods for accurate measurements ofcoupling, mainly focusing on pure shift based 2D orthogonal-pattern and phase-sensitive 2DRESspectroscopy and their applications in overcoming strong coupling effects and field inhomogeneities.

nuclear magnetic resonance (NMR),-resolved spectroscopy,phase-sensitive,G-SERF,coupling constant, pure shift

O482.53

A

10.11938/cjmr20212929

2021-06-29;

2021-08-10

国家自然科学基金资助项目(U1805261, 22073078, U1632274, 11675135和11761141010).

* Tel: 0592-2183301, E-mail: chenz@xmu.edu.cn.