基于单端电压行波传输规律的柔直架空线路金属性接地故障测距方法

李博通，黄旭华，李春波，苏 江

（天津大学电气自动化与信息工程学院智能电网教育部重点实验室，天津 300072）

基于电压源型换流器、以全控型可关断电力电子器件为核心元件、采用脉冲宽度调制技术的新型高压直流输电，以其有功无功独立控制、无换相失败及无功补偿问题等诸多优势，在远距离大容量输电和分布式能源并网等方面有巨大发展潜力[1-3]。在柔性直流输电发展早期，为降低输电线路的故障率，提高电力系统的可靠性，多采用直流电缆作为输电导体[4-5]。近年来，随着电压等级的不断提高和输送距离的增加，实际工程中广泛采用经济性更好的架空线来进行电能传输[6-7]。无论是直流电缆还是架空线，线路发生故障后快速准确地直流故障测距，对于减轻巡线人员负担、快速恢复供电以及提高电力系统稳定性具有重要的理论意义与实际工程价值。

根据测距原理的区别，目前直流故障测距方法主要分为行波法[8-11]和故障分析法[12-14]两大类。行波法主要根据故障时暂态行波的传播特性，通过识别故障行波波头到达测量点的时刻或提取故障行波多次折反射形成的固有频率主成分来进行故障测距。文献[8]对故障暂态行波进行小波变换，通过小波变换模极大值的极性，识别反射波的波头并将其消除；文献[9]利用小波神经网络拟合行波特征值与输电线路故障距离之间的关系，构建小波神经网络模型进行故障测距；文献[10]利用小波变换得到的固有频率主成分与故障距离的关系进行故障测距；文献[11]通过在重合闸期间重合残余电流开关向故障线路注入电压，利用该电压行波的固有频率与故障距离的关系进行故障测距。总之，通过检测故障行波波头到达时刻的行波法测距速度快、精度高，但采样率要求较高，且在经过渡电阻故障时存在波头识别困难的问题；而利用行波固有频率与故障距离关系的行波测距法对采样率的要求低，但能否准确提取故障行波的固有频率将直接影响该方法的测距精度。

故障分析法主要根据线路参数与测得的电气量之间的关系列写电路方程，通过对方程的求解实现故障测距。目前故障分析法的发展主要受线路模型和参数准确度的制约。文献[12]将遗传算法与故障测距原理相结合，将线路参数作为遗传算法的约束条件，在一定范围内对线路参数进行取值，减小了线路参数不准确情况下的故障测距误差；文献[13]利用神经网络算法中的训练思想，预先对各种故障模式进行模拟，引入Pearson相关度系数，将故障后电压信号与模拟故障模式的相似度进行比较实现故障测距。以上方法均是通过智能算法对测距结果进行修正，并未从根本上解决输电线路模型及参数不准确对测距结果造成影响的问题。文献[14]考虑了直流输电线路参数的频变特性，提取暂态过程中的各频率分量，在各个频率点下利用相应的线路参数进行故障定位，一定程度上提高了模型的准确性，但该方法的测距结果在频率分量提取不准确时存在较大误差。综上，故障分析法对采样率低且可靠性高，但受线路模型和参数的准确度等因素的影响很大。

本文针对双极运行方式下的高压柔性直流输电系统，分析了故障发生后故障点的边界条件，基于线路频率相关模型，研究了故障发生后输电线路上电压行波的传播特性，在此基础上提出了一种基于正反向行波关系直流架空输电线路单端量故障测距原理。

1 单极接地故障边界条件分析

柔性直流输电系统往往采用双极运行方式。双极运行方式下的真双极柔性直流输电系统单极接地故障示意如图1所示，其中正极线路点k处发生单极接地故障。图中：m端为输送功率端，n端为接收功率端，m、n两端换流站分别包含2个相同的正负极换流器，每个换流器通过一组换流变压器与交流母线连接，换流站内2个换流器的中性点均直接接地；imp(t)和ump(t)分别是正极线路首端的测量电流和测量电压；imn(t)和umn(t)分别是负极线路首端的测量电流和测量电压；ukp(t)和ikp(t)分别是正极线路上故障点k处的电压和接地故障电流；imkp(t)是正极线路上由首端m侧传向故障点k的电流；考虑到两条线路之间存在耦合，在非故障极上与k对应的位置假设一个虚拟故障点，ukn(t)和ikn(t)分别是负极线路上虚拟故障点处的电压和接地故障电流；imkn(t)是负极线路上虚拟故障点处由首端m侧传向虚拟故障点的电流。设lmn表示架空输电线路的总长度，lmk表示输电线路首端m侧到故障点k处的距离。

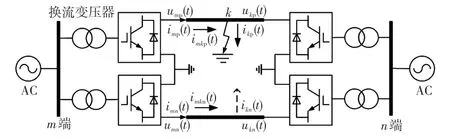
图1 双极运行方式下的两端柔性直流输电系统单极接地故障示意Fig.1 Schematic of double-terminal flexible HVDC system under unipolar grounding fault operating in bipolar mode

若在正极输电线路的故障点k处发生的是金属性接地故障，那么在故障点处有

凯伦贝尔矩阵S是一种常用的模量变换矩阵，其表达式为

利用凯伦贝尔变换矩阵将故障点k处的正负极电压和电流进行解耦，得到故障点处电压和电流的地模分量与差模分量，即

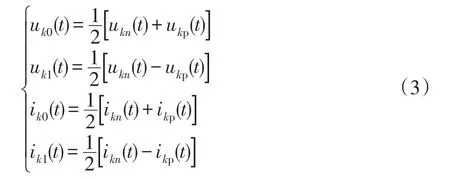
式中：uk0(t)和ik0(t)分别为故障点处电压和电流的地模分量，uk1(t)和ik1(t)分别为故障点处电压和电流的差模分量。

将式（3）代入式（1），可以得到单极接地故障的边界条件为

2 单极接地故障后输电线路上的电压行波传输特性分析

根据文献[15]，线路特征阻抗的地模分量Zc0(f)和差模分量Zc1(f)以及特定线路长度l下传播系数的地模分量A0(f)和差模分量A1(f)的表达式分别为

式中：l为行波传输路径总长度；R0(f)和R1(f)分别为正极和负极输电线路上电阻参数的地模分量和差模分量；L0(f)和L1(f)分别为电感参数的地模分量和差模分量；C0和C1分别为电容参数的地模分量和差模分量。

利用式（5）和式（6）计算特征阻抗和传播系数的地模分量和差模分量的频域值，对其进行时域反变换，即可得到特征阻抗地模分量的时域值zc0(t)和差模分量的时域值zc1(t)，以及传播系数地模分量的时域值a0(t)和差模分量的时域值a1(t)。

利用凯伦贝尔变换矩阵对测量电压和测量电流进行解耦。将正极和负极输电线路首端m侧的测量电压ump(t)和umn(t)解耦，得到线路首端m侧测量电压的差模分量um1(t)和地模分量um0(t)分别为

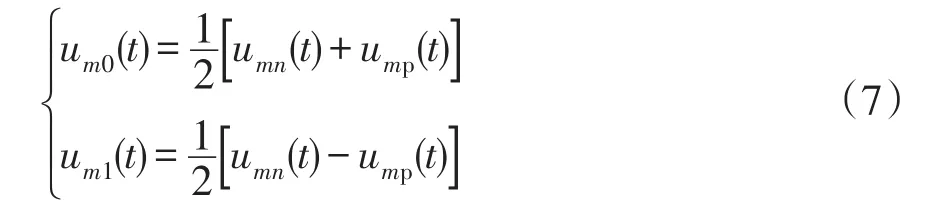
将正极和负极输电线路首端的测量电流imp(t)和imn(t)解耦，得到线路首端m侧测量电流的差模分量im1(t)和地模分量im0(t)分别为

以差模分量为例，对故障后输电线路上的电压行波传输规律进行分析。

正极线路发生单极接地故障后，由单一模量行波的传播公式可以得到输电线路首端m侧正向电压行波差模分量和故障点k处的正向电压行波差模分量的关系，即

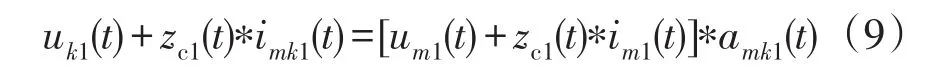
式中：*代表卷积运算；amk1(t)为输电线路首端m侧到故障点k处之间线路的传播系数的差模分量，其值与故障距离lmk有关；imk1(t)为由线路首端m侧传向故障点k的电流的差模分量。

同理，可得到输电线路首端m侧的反向电压行波的差模分量与故障点k处的反向电压行波的差模分量之间的关系，即

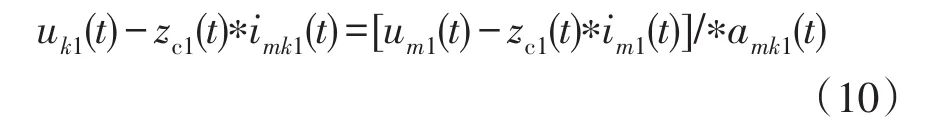
式中，/*代表反卷积运算。

式（9）和式（10）相加后可以得到故障点电压行波差模分量的关系式，即

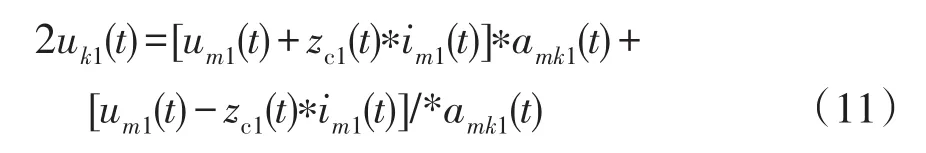
故障点电压行波地模分量的关系式为

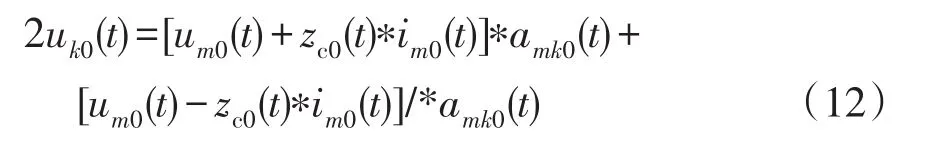
式中，amk0(t)为输电线路首端m侧到故障点k处之间线路传播系数的地模分量，其值与故障距离lmk有关。

联立式（11）、式（12）和式（4），可以得到故障线路上的行波关系为

为避免做更为复杂的反卷积运算，将式（13）等号两边同时做卷积amk1(t)∗amk0(t)，可以得到

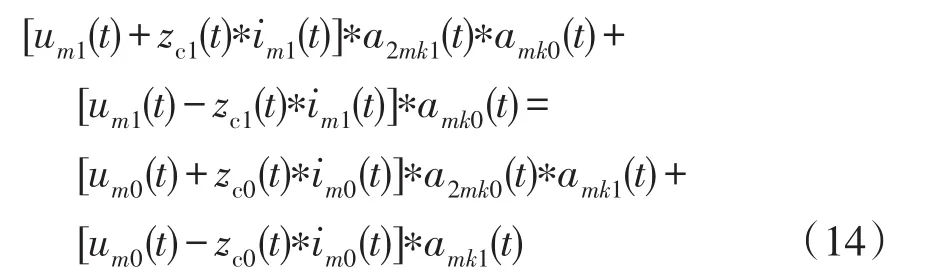
式中：a2mk1(t)为2倍故障距离2lmk长度的输电线路对应传播系数的差模分量，其值与2lmk有关；a2mk0(t)为2倍故障距离2lmk长度的输电线路对应传播系数的地模分量，其值与2lmk有关。

令故障线路上的正向行波为F（t），反向行波为B（t），分别表示为

当正极输电线路上某k点处发生金属性接地故障时，线路上正、反向电压行波及测量电压和测量电流之间满足式（16）中的关系。

3 金属性单极接地故障测距方法

3.1 故障测距原理

当且仅当amk0(t)和amk1(t)分别表示实际故障距离lmk长度的线路所对应的地模传播系数和差模传播系数、a2mk0(t)和a2mk1(t)分别表示2倍实际故障距离2lmk长度的线路所对应的地模传播系数和差模传播系数时，式（16）成立。由于式（16）中的传播系数项均与故障距离有关，所以在故障距离未知的情况下所有传播系数项也是未知量。

3.2 故障测距算法

为了准确求解故障距离，假设有多个不同的故障距离，通过求解对应长度线路的相应传播系数模量并代入式（16）计算，验证是否满足等式的方式来进行故障测距。其中，使得式（16）成立所对应的假设故障距离即为计算故障距离。

对于一段长度固定的架空输电线路而言，为提高故障测距结果的精度，应当假设尽可能多的故障距离个数。在线路上设置N个假设故障距离，N与线路长度有关，N=[l/Δl]+1，Δl为设定的单位长度，其值按照波速v乘以采样周期Ts设置。以图1所示的真双极两端柔性直流输电系统中架空输电线路为例，架空线路总长度为lmn，第i个假设故障距离为li=(i- 1) Δl(i= 1,2,…,N)，分别对式（16）的左侧值和右侧值进行计算，每计算完一次记录结果，并将li增加Δl再进行下一次计算，直到li>lmn为止。最终得到所有假设故障距离下式（16）对应的左侧值和右侧值的时域曲线。其中，左侧值和右侧值的时域曲线重合度最高时对应的假设故障距离为实际故障距离。

单极接地故障测距算法流程如图2所示。

图2 单极接地故障测距算法流程Fig.2 Flow chart of unipolar grounding fault location algorithm

具体计算过程如下。

步骤1柔性直流输电线路某k点处发生单极接地故障后，首先利用卡松公式计算出线路的zc(t)，并保持与zc(t)相同的采样频率对首端m侧故障电压ump(t)、umn(t)和故障电流imp(t)、imn(t)进行采样，数据窗长与zc(t)长度相同。

步骤2假设故障距离为li=(i- 1) Δl，其中Δl=vTs。设i=1，对于此特定长度为li的输电线路而言，可利用卡松公式计算得到长度分别为li和2li的输电线路的传播系数ai(t)和a2i(t)。

步骤3计算该假设故障距离下不同采样点处对应式（16）左侧和右侧的差值Dif(x)。

步骤4根据式（18）计算Dif(x)中所有元素值的均方差。

步骤5不断增加i值并重复步骤2～4，直到满足li=(i- 1) Δl>lmn，循环结束。

步骤6计算所有中的最小值，该值对应的假设故障距离即为实际故障距离lmk。

3.3 过渡电阻对故障测距的影响分析

4 仿真验证

4.1 单极金属性接地故障测距算法的仿真验证

在PSCAD/EMTDC仿真环境中搭建图1所示的两端柔性直流输电系统模型。线路全长为100 km，直流侧额定电压为±500 kV，额定功率为3 000 MW。输电线路采用频率相关模型，参数设定如下：两根导线的对地平均高度为30 m，弧垂为10 m，导线半径为0.020 3 m。采样频率设置为106Hz，时间窗长为2.048 ms，Δl为0.3 km（波速乘以采样周期）。

以1.0 s时刻距离线路首端50 km处发生金属性接地故障为例进行仿真分析。首先，采样故障发生后正负极线路首端m侧的电压和电流，在2.048 ms内采到2 048个采样点。设置利用卡松公式计算线路特征阻抗zc(t)和传播系数a(t)时的长度为2 048，则卷积zc(t)∗im(t)计算结果中前后各2 047个点为不完全卷积点，应舍弃，只有第2 048点为完全卷积的点。为了解决上述问题，在计算zc(t)∗im(t)时将2个相同的im(t)周期延拓为含有4 096个点的新数组，则zc(t)∗im(t)的第2 049～4 096点均为完全卷积点，即为zc(t)∗im(t)的正确计算结果。其他卷积计算采用同样的方法。

假设故障距离li分别设为0，0.3，0.6，…，99.9 km，分别计算出长度为li和双倍故障距离2li的输电线路对应的传播系数的地模分量a01(t)和a02(t)以及差模分量a11(t)和a12(t)。为了避免故障初期的瞬间波动对计算结果产生误差，式（16）左侧和右侧差值从故障发生1.0 ms后计算结果开始取值。li分别为30.0、40.2、50.1和60.0 km时式（16）左侧值和右侧值的曲线如图3所示。

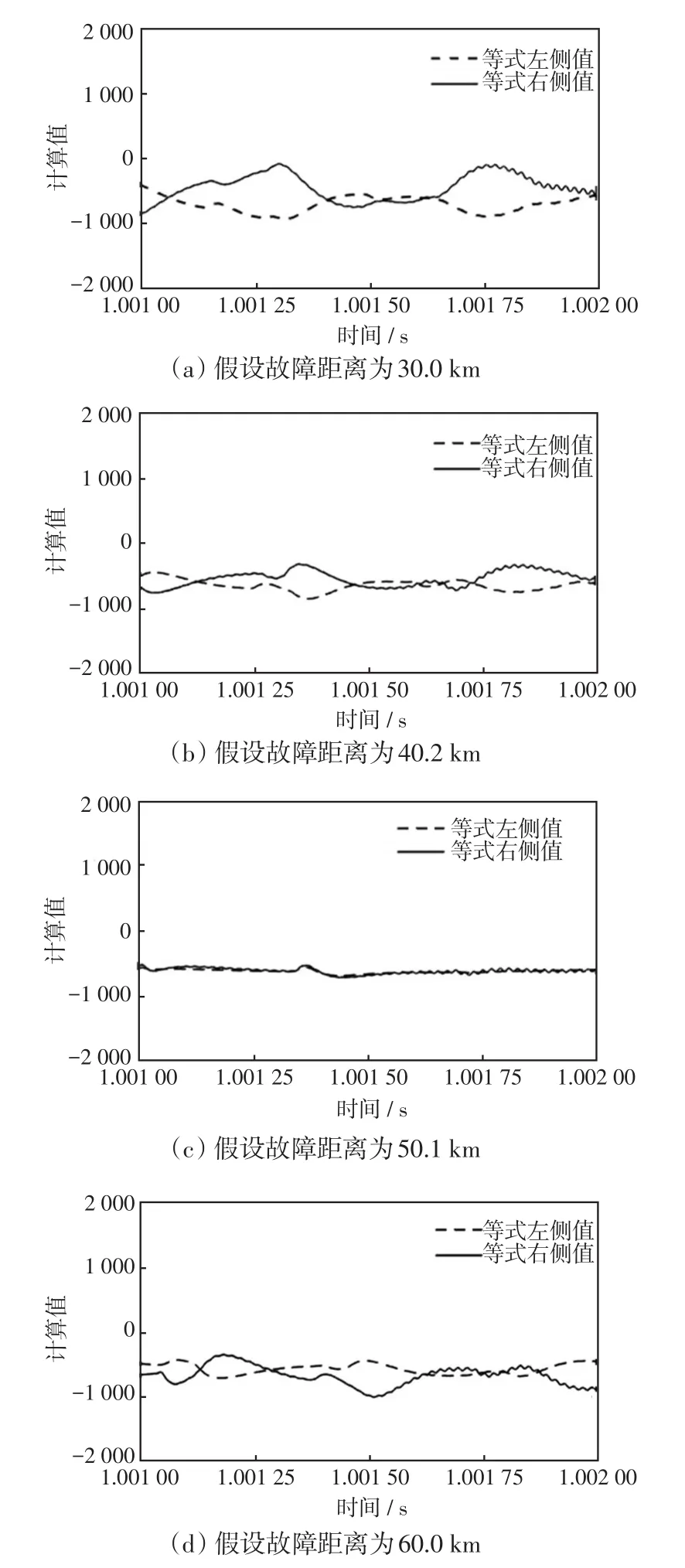
图3 不同假设故障距离下式（16）左侧值和右侧值曲线Fig.3 Curves of left-and right-side values of Eq.（16）under different assumed fault distances

从图3可以看出：只有当假设故障距离与实际故障距离十分接近时，故障后式（16）左侧值和右侧值的曲线才会高度重合，如图3（c）所示；而当假设故障距离与实际故障距离相差较远时，式（16）左侧值和右侧值曲线的重合度很低。

根据式（18）对50 km处发生故障时不同假设故障距离下式（16）左侧和右侧差值的均方差进行计算，结果如图4所示。

图4 50 km处发生故障时各假设故障距离下式（16）左侧和右侧差值的均方差Fig.4 Mean squared error of Dif(x ) under eachli when the fault distance is 50 km

通过计算可得所有假设故障距离对应的多个不同的均方差。在所有均方差中最小值所对应的假设故障距离li为49.5 km，也即计算得到的故障距离为49.5 km，与实际故障距离50 km的绝对误差为0.5 km。

分别在 0、10、20、30、40、60、70、80、90和 100 km处设置金属性接地故障，按照上述方法求得不同假设故障距离下式（16）左侧和右侧差值的均方差。实际故障距离分别为10 km和70 km时，不同假设故障距离下式（16）左侧和右侧差值的均方差计算值如图5所示。取均方差最小值对应的假设故障距离即为实际故障距离，不同故障位置下的测距结果及误差如表1所示。

图5 不同实际故障距离时各个假设故障距离下式（16）左侧和右侧差值的均方差Fig.5 Mean squared error of Dif(x ) under eachliin the case of different actual fault distances

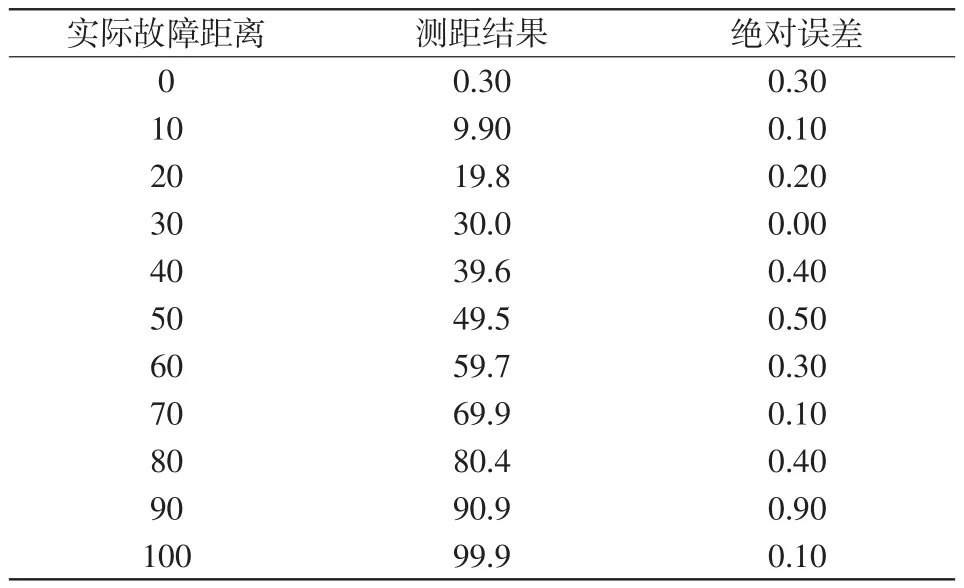
表1 金属性接地故障测距结果及误差Tab.1 Location results and errors of fault distance in the case of metallic grounding fault km

由图5可以看出，当实际故障距离分别为10 km和70 km时，等式（16）左侧和右侧差值的均方差均在实际故障距离附近取得最小值，且该最小值对应唯一的假设故障距离。

由表1可知，本算例全长100 km的线路中最大测距绝对误差为900 m，误差在可接受范围内。仿真表明所提单极接地故障测距方法具有较高测距精度。

4.2 过渡电阻对测距算法的影响分析及仿真验证

为了验证过渡电阻对测距算法的影响，分别设置过渡电阻为30 Ω和100 Ω的单极接地故障。不同故障距离下的测距结果及误差如表2所示。

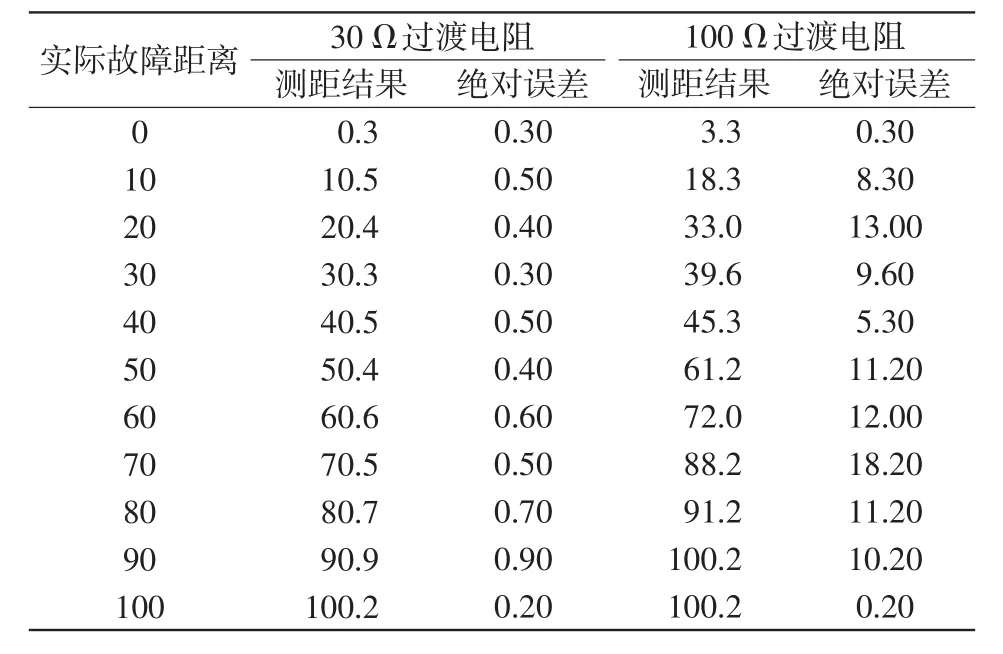
表2 经不同过渡电阻接地时的测距结果及误差Tab.2 Location results and errors of fault distance in the case of different transition resistances km

由表2可知：当经30 Ω过渡电阻发生接地故障时，本算例全长100 km的线路中最大测距绝对误差为900 m，误差在可接受范围内；当经100 Ω过渡电阻发生接地故障时，本算例全长100 km的线路中最大测距绝对误差为18.2 km，且各误差普遍较大，超出了可接受范围，严重影响了故障测距的可靠性。

综上所述，本文所提出的故障测距原理具有一定的抗过渡电阻的能力，但在过渡电阻过大时测距结果会有较大误差，可靠性也受到严重影响。

4.3 噪声对测距算法的影响分析及仿真验证

为了分析不同水平噪声对测距算法的影响，以1.0 s时刻距离线路首端50 km处发生金属性接地故障为例，测量电气量不同信噪比下测距结果的绝对误差，如图6所示。

图6 不同信噪比下测距结果的绝对误差Fig.6 Absolute error of location results at different signal-to-noise ratios

由图6可见：当信噪比大于43 dB时，绝对误差均在1.0 km以内，在可接受范围内；当信噪比小于43 dB时，测距误差变大，测距算法失效。

通过对不同故障距离下不同水平的噪声信号对测距结果影响的仿真可知，在噪声水平较低的条件下该测距方法仍然有较高的测距精度，但当噪声水平较大时测距结果会有较大误差，可靠性也受到严重影响。因此本文提出的单端量单极接地故障测距方法具有一定的抗干扰能力。

5 结语

本文提出了一种在高压柔直系统中架空线路单极接地故障的单端量故障测距原理。以架空线的频率相关模型和行波的传播方程为基础，研究了架空输电线路发生单极接地故障后的边界条件以及输电线路上正向行波和反向行波的传播特性，明确了正反向行波差模分量和地模分量之间的关系。在此基础上，提出了一种在单极接地故障下可以实现精确故障定位的故障测距原理及算法。在PSCAD中对系统进行建模并用MATLAB编程计算，验证了所提故障测距原理及算法的有效性和准确性，并分析了过渡电阻及不同水平噪声对所提故障测距原理的影响。结果表明，本文所提单端量故障测距原理可以在全线范围内针对金属性接地故障精确地故障定位且具有一定的抗过渡电阻的能力。