基于反函数抛物线插值的滤波器容量配置方法

窦 飞，程保华，程锦闽，刘增训，刘天阳，陈麒宇

（1.国网江苏省电力有限公司，南京 211106；2.天津城建大学控制与机械工程学院，天津 300384；3.国家电网有限公司，北京 100031；4.中国电力科学研究院电网安全与节能国家重点实验室，北京 100192）

换流站在整流和逆变运行时，都将消耗无功功功率，若未能对其进行有效无功补偿，将导致交直流系统间产生过多无功交换，引发交流电压较大的变化，严重时会使直流输电系统不能有效运行[1-2]。交流滤波器既能提供容性无功功率补偿，亦可抑制直流系统产生的谐波分量。换流站交流滤波器容量配置是直流系统设计的重要环节[3-4]。

通过计算公式确定换流站无功消耗[5]，依其可配置交直流系统无功交换量限值条件下所需的交流滤波器容量。但由于换流站无功功率消耗与交直流系统参数的非线性关系，以及交流滤波器实际提供无功功率与交流电压的耦合关系[6-7]，依换流站无功消耗计算方法确定的交流滤波器配置容量与实际运行存在一定偏差。规划阶段的直流输电系统往往借助潮流计算验证配置容量的合理性。

潮流计算可准确确定交直流系统限值时需配置的交流滤波器容量，亦可准确计算交流滤波器投入后交直流系统间无功交换量[8]。交流滤波器配置容量的准确确定具有非常重要的意义[9-10]。一方面，其可防止配置容量不足造成的直流输电系统运行不稳定和配置过剩造成的投资多问题，为无功分组提供准确依据；另一方面，准确计算交流滤波器投入后交直流系统间无功交换量对于交流电网过电压的研究也至关重要[11]。

采用反复潮流计算[12]可确定交直流系统间无功交换量限值时所需的交流滤波器配置容量，但由于潮流计算本身耗时较长，导致该过程需要较长时间。通过潮流计算获取几组交流滤波器配置容量和交直流系统间无功交换量数据后，目前一般采用线性插值法或直接原函数抛物线插值确定所需交流滤波器配置容量。一方面，由于线性插值误差较抛物线插值误差大，同样精度条件下，线性插值比抛物线插值需要更多潮流计算数据；另一方面，由于直接原函数抛物线插值需要求解一元二次方程和人工判断物理解。故本文提出一种基于反函数抛物线插值确定换流站交流滤波器配置容量的方法，该方法不需要精确计算换流站本身的无功消耗，不需要使用电磁仿真工具对换流站进行精细建模，能依据交直流系统无功交换量限值快速确定所需交流滤波器配置容量。

本文方法借助PSD-BPA潮流计算程序确定交流电网经由公共连接母线注入换流变压器的无功功率量，依据交直流系统两侧的无功交换量限值，基于反函数抛物线插值法确定所需交流滤波器配置容量。

1 换流站无功构成与无功消耗

1.1 换流站无功构成

交直流系统换流站内无功构成如图1所示。换流站与交流系统的无功交换表示为

图1 换流站无功构成Fig.1 Reactive power composition of converter station

式中：Qd为换流站无功功率消耗；Qfilt为交流滤波器实际提供的无功功率；Qswap为换流站与交流系统无功交换量，其为正表示交流系统向换流站注入无功功率，其为负表示换流站向交流系统注入无功功率。

换流站内换流器和换流变压器是站内无功消耗的主体。换流器在整流和逆变过程中为实现交直流转换均需消耗无功功率；换流变压器在空载和带负荷时均需消耗一定的无功功率；交流滤波器和交流系统是换流站内提供无功功率的主体，需要交流滤波器配置容量和换流站内无功消耗相匹配，才能限制换流站与交流系统无功交换量在限值以内。

1.2 换流站无功消耗

换流站无功消耗受交流系统和直流系统参数的影响。交流系统参数包括换流站接入点的电压等级、实际运行电压、无功支持能力等；直流系统参数包括直流电压、直流电流、直流运行控制方式等。加之设备参数公差和测量与控制误差等因素的影响，换流站消耗的无功功率是动态变化的，这使得难以通过换流站无功消耗计算公式准确匹配所需交流滤波器配置容量。换流站无功消耗计算公式为

式中：Pd为直流有功功率；μ为换流器换相角；α为换流器触发角。

同时，交流滤波器实际提供的无功功率与标称电压下无功功率存在的关系[13]为

因交流滤波器容量是针对标称电压的，所以交流滤波器投入后实际提供无功功率受交流电压影响，且交流电压又会被交流滤波器的投入量所影响。上述耦合关系使得不能简单按照计算公式确定的换流站无功消耗配置交流滤波器容量。

1.3 交直流系统无功交换限值

交流系统提供无功和吸收无功能力决定了交直流系统无功交换限值范围[14]。换流站提供无功和吸收无功的能力受电源集中程度、运行电压等级和负荷水平等的影响。

（1）交流系统提供无功与交直流系统无功交换限值。若换流站附近电厂具备较大无功出力水平，从换流站可靠运行和减少交流滤波器投资角度考虑，交流系统向换流站提供部分无功，交直流系统无功交换限值取一定的非负值。

（2）交流系统吸收无功与交直流系统无功交换限值。若换流站靠近负荷中心，交流系统电压较低，交流系统具备一定的无功吸收能力，考虑换流站无功消耗全部站内补偿，交直流系统无功交换限值取一定的非正值。

在交直流系统参数一定的情形下，根据规划设计的直流传输有功功率Pd和初算的换流站无功消耗Qd，依据交直流系统无功交换限值，借助潮流计算可准确确定所需交流滤波器配置容量。

2 潮流计算方程与潮流求解分析

2.1 潮流计算方程

潮流计算根据给定的电力系统运行条件和网络结构确定整个系统的运行状态，通过潮流计算[15]可确定交直流系统间的无功交换量。按照交流系统节点上是否连接换流变压器，节点分为直流节点和纯交流节点。

2.1.1 交流节点功率方程

对于纯交流节点，其功率方程为

式中：Pi、Qi分别为节点i向电力系统注入的有功功率和无功功率；Ui、Uj分别为节点i、j的电压向量；Ps,i、Qs,i分别为节点i的给定有功功率和无功功率；θij为节点i、j的电压相角差；Gij为节点电导矩阵；Bij为节点电纳矩阵；na为纯交流节点数目。

2.1.2 直流节点功率方程

对于两端直流系统，直流节点功率方程为

式中：k为换流变压器及所连换流器的编号，对于两端直流系统，k=1对应整流器，k=2对应逆变器，正负号分别对应逆变器和整流器；Pd,i、Qd,i分别为换流变压器从直流节点i抽出的基波有功功率和基波无功功率，Pd,i=Ud,kId,k，Qd.i=Ud,kId,ktanφk，其中，Ud,k和Id,k分别为k号换流变压器所连换流器直流电压和直流电流，φk为功率因数角。与纯交流节点功率方程相比，直流节点功率方程包含新的变量Ud,k、Id,k和φk，则补充换流器方程为

式中：Nk为换流变压器变比；αk为换流器触发角；Xk为换流变压器等值感抗；λγ为换流器触发角和换相角的关系系数，取值λγ=0.995。

2.2 潮流求解分析

2.2.1 潮流求解过程

直流系统对交流系统的作用通过换流变压器从交流系统抽出或注入的功率Pd,i+jQd,i产生，交流系统对直流系统的作用通过换流变压器一次侧电压Ui产生[16]。当换流站从交流系统抽出或注入的功率已知时，交直流系统潮流计算便可独立求解。

求解交流系统方程时，将直流系统采用接在相应节点上的已知有功和无功功率等值。求解直流系统方程组时，将交流系统等值成加在交流母线上的一个恒定电压。迭代求解过程中，交流系统方程组的求解为其后的直流方程组求解提供交流母线电压值，而直流方程组的求解为下一次迭代中交流系统方程组提供换流站的等值有功和无功功率，如此循环，直至收敛。

2.2.2 两端直流系统潮流计算求解分析

对于两端直流输电系统，若已知直流有功功率为Pd,k，整流侧采用定功率控制方式，逆变侧采用定电压控制方式，依据交直流系统独立潮流进行求解分析。

1）交流系统节点电压Ui的幅值和相角

依据交流节点有功功率和无功功率，可确定交流节点电压幅值和相角。根据规划设计的直流传输有功功率Pd,k，以及换流变压器从交流系统抽出或注入的无功功率Qd,k可由式（2）初定。根据已知交流节点的有功功率和初定的无功功率，由式（4）可确定交流节点电压Ui幅值和相角。交流节点电压即为换流变压器一次侧电压，当该值确定后，换流器方程式（6）可独立求解。

2）直流系统待求量

换流变压器一次侧电压Ui确定后，两端直流系统待求量为整流和逆变换流器的10个量：直流电压Ud,k、直流电流Id,k、换流器触发角αk、功率因数角φk和换流变压器变比Nk。

整流侧采用定功率控制方式和逆变侧采用定电压控制方式时，依据直流系统稳态运行控制中尽可能使其直流电压在额定电压附近的原则和功率因数尽可能高的原则，可确定换流器触发角αk。结合两端直流系统直流电压和直流电流关系，给定直流电压迭代初值后，可完成直流系统待求量求解，计算公式为

式中：R为两端直流输电线路电阻；Pds,1为整流侧定功率设定值；Uds,2为逆变侧定电压设定值；αs,1为整流换流器控制角设定值；αs,2为逆变换流器控制角设定值。

3 确定交流滤波器配置容量方法

3.1 交流滤波器配置容量确定过程

本文采用基于反函数抛物线插值的方法确定交直流系统无功交换量限值时所需交流滤波器配置容量。该方法需借助PSD-BPA潮流计算确定三组交流滤波器配置容量和对应交直流系统无功交换量数据。

基于反函数抛物线插值的交流滤波器配置容量确定过程中，首先获取两端直流输电系统有功功率，其次依据换流站无功消耗计算公式确定换流站无功消耗，进而确定交流滤波器配置容量初始值，然后根据所述有功功率值和交流滤波器配置容量初始值，采用PSD-BPA潮流程序计算换流站与交流系统的无功交换量，此时对应的交流滤波器配置容量和交直流系统无功交换量为第1组数据。按照上述流程，经过3次迭代确定该方法所需的3组数据。利用上述3组数据，采用反函数抛物线插值方法，依据交直流系统无功交换量限值，确定所需交流滤波器配置容量。其具体实现过程如下。

根据交直流系统无功交换量限值Qswap，可直接确定所需交流滤波器配置容量Qfilt。在交直流系统无功交换量为0的理想情形下，交流滤波器配置容量Qfilt=a͂20。

3.2 理论分析

已知几组交流滤波器配置容量和相应交直流系统无功交换量数据，通过插值法可确定交直流系统无功交换量限值条件下换流站所需交流滤波器配置容量。

对Qswap=Qd-Qfilt的插值求解可表示为

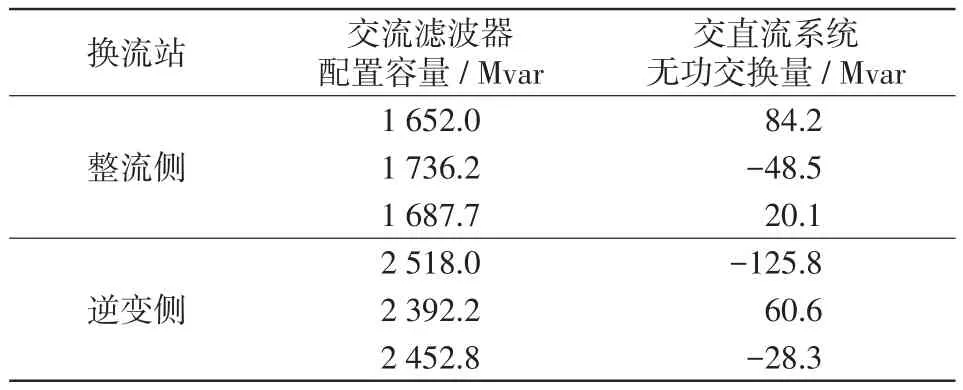
定义：设函数f(x)在区间[a,b]上有定义，且a≤x0

则称φ(x)是f(x)的插值函数。其中，x对应交流滤波器配置容量；y对应交直流系统无功交换量。3组潮流数据(Qfilt,1,Qswap,1)、(Qfilt,2,Qswap,2)、(Qfilt,3,Qswap,3)分别记作(x1,y1)、(x2,y2)、(x3,y3)。

3.3 插值方法

3.4 插值余项

因交流滤波器配置容量和交直流系统无功交换量的非线性耦合关系，其被插值函数f(x)的阶次n≥2。抛物线插值多项式更接近交流滤波器配置容量和交直流系统无功交换量的函数关系，抛物线插值法误差比线性插值法误差小。

综上所述，基于反函数抛物线插值法确定交流滤波器配置容量有如下的优势。

（1）基于反函数抛物线插值余项阶次比线性插值余项阶次高，因交流滤波器配置容量和交直流系统无功交换量的非线性耦合关系，抛物线插值误差比线性插值误差小。

（2）基于反函数抛物线插值法与线性插值法相比，同样精度要求条件下，前者所需潮流计算次数少于后者。在交直流系统无功交换限值条件下，基于反函数抛物线插值法只需3次潮流计算确定3组数据，就能以较高精度逼近所需交流滤波器配置容量；而线性插值法至少需要4次潮流计算才能达到相近精度。

（3）基于反函数抛物线插值法与基于原函数抛物线插值法相比，同样精度要求条件下，前者计算速度更快。基于原函数抛物线插值法确定所需交流滤波器配置容量时需进行开方运算，且一元二次方程求解后存在2个解，需根据物理意义进行人工判断。基于反函数抛物线插值法不需要求解一元二次方程，可直接确定所需交流滤波器配置容量，计算速度快。

4 计算验证

某规划阶段的两端直流输电系统，直流传输有功功率为4 000 MW，直流输电系统整流侧采用定功率控制，逆变侧采用定电压控制，控制参数如表1所示，采用PSD-BPA进行潮流计算。

表1 高压直流系统控制参数Tab.1 Control parameters of HVDC system

表2给出了通过潮流计算确定的3组整流侧和逆变侧换流站交流滤波器配置容量和对应交直流系统无功交换量数据。

表2 换流站3组潮流计算数据Tab.2 Three groups of power flow calculation data about converter stations

根据表2给出的3组数据，在交直流无功交换量限值为0时，采用线性插值法、基于原函数抛物线插值法和基于反函数抛物线插值法计算得到的整流侧和逆变侧交流滤波器配置容量结果如表3所示。

表3 不同方案交流滤波器配置容量比较Tab.3 Comparison of AC filter configuring capacity among different schemes

由表3并结合插值余项可知，抛物线插值余项阶次比线性插值余项阶次高，因交流滤波器配置容量和交直流系统无功交换量的非线性耦合关系，抛物线插值误差比线性插值误差小。4次潮流计算后采用线性插值法和3次潮流计算后采用抛物线插值法计算得到的交流滤波器配置容量接近，抛物线插值法比线性插值法潮流计算次数少1次，完成一次潮流计算的时间约25 s。即使在离线计算模式下，节省的时间对于工程人员和计算资源都有一定意义，更重要的是抛物线插值法在节省时间的同时兼顾准确性。原函数抛物线插值法和反函数抛物线插值法所需潮流计算次数相同，计算得到的交流滤波器配置容量均接近实际换流站无功消耗，但原函数抛物线插值法的解需要人工判断，其不但增加了工程人员的操作，而且使得计算时间存在不确定性。

5 结语

本文提出一种基于反函数抛物线插值确定换流站交流滤波器配置容量的方法，其能按交直流系统无功交换限值快速准确配置交流滤波器容量。本文方法根据直流输电系统传输的有功功率，初算交流滤波器配置容量初始值，然后按照潮流计算方程利用PSD-BPA潮流计算程序确定交直流系统无功交换量。按上述过程确定3组交流滤波器配置容量和交直流系统无功交换量，基于反函数抛物线插值法确定所需交流滤波器配置容量。

本文方法不需要电磁仿真工具对直流换流站进行精细建模，也不需要精确计算换流站无功消耗，同时还兼顾了交流滤波器投入后实际提供无功功率与交流电压的相互影响，能准确快速确定交直流系统无功交换限值条件下所需交流滤波器配置容量，对直流输电工程具有一定应用价值。