CLLLC谐振式变换器的广义预测控制

吴 蒙，于新红，汪凤翔，张 伟

（1.电机驱动与功率电子国家地方联合工程研究中心（中国科学院海西研究院泉州装备制造研究所），泉州 362216；2.宁德时代新能源科技股份有限公司，宁德 352106）

隔离型高频双向DC/DC变换器具有高安全可靠性、高能量密度和高转换效率等优点，近年来在直流微网、电动汽车、大容量储能系统等需要能量双向流动的场合得到广泛的应用。为满足直流变换器的性能需求，进一步减小变换器体积，提升传输效率，变换器的工作频率通常较高。广受关注的隔离型双向移相全桥型DC/DC变换器具有拓扑简单、调制策略多样等特点，但是该型拓扑也存在调制范围窄及软开关实现条件较为严格等问题[1][2]。文献[3]提出的CLLLC谐振式双向DC/DC变换器在传统LLC变换器的基础上增加了LC谐振网络，使得该拓扑具有良好的对称性，变换器在正向和反向运行时具有相似的特性，且保留了LLC变换器良好软开关特性，可以实现全负载范围的软开关，从而达到较高峰值效率。CLLLC谐振式双向DC/DC变换器通常采用比例积分PI（proportion integral）控制器实现闭环控制作用。但由于谐振变换器的数学模型复杂，导致控制器参数难以设计，在实际工程应用中需要繁琐的PI参数整定过程[4]。

随着微控制器性能的不断提升，预测控制（pre⁃dictive control）、滑模控制（sliding-mode control）、鲁棒控制（robust control）等一些先进控制方法在电力电子变换器领域的应用迅速发展[5][6]。有限集模型预测控制FCS-MPC（finite control set-model predictive control）通过建立变换器和负载的离散模型，在每个当前控制周期根据成本函数计算下一控制周期最优开关状态，产生最优电压矢量，相比于传统的控制方法具有更好的动态性能。但是，由于CLLLC谐振式变换器的多模态特性和非线性特性，导致变换器建模复杂[7]，因此限制了有限集预测控制的应用。

文献[8]基于LLC变换器的大信号模型设计了滑模控制策略，大幅提高了变换器的动态性能，且具有较强的鲁棒性，但输出电压的纹波较大；文献[9-10]提出了一种基于变换器谐振电容电压的Bang-Bang控制方法，具备快速的动态性能。但是这种策略需要相应的硬件电路产生PWM信号，增加了系统成本；文献[11]详细阐述了CLLLC谐振式变换器的运行原理、调制策略和设计方法，在输出电压反馈的基础上提出一种输入前馈电压控制，有效提高了系统稳态与动态特性，但控制器仍为PI控制策略，且基于变换器模型设计PI参数的过程并未阐明，系统动态性能也有待进一步提高。

基于以上文献成果及其存在的问题，本文提出一种基于低阶等效模型的广义预测电压控制算法。首先，通过小信号扫频的方法拟合出变换器低阶等效模型，其次基于低阶等效模型设计一种广义预测电压控制策略，提升系统稳态及动态性能，实现CLLLC谐振式DC/DC变换器的高性能控制。

1 工作原理及数学模型

1.1 CLLLC谐振式变换器主拓扑分析

CLLLC谐振式双向DC/DC变换器拓扑如图1所示。图中：S1～S4组成变压器一次侧H桥，S5～S8组成变压器二次侧H桥，Coss1～Coss8为开关管的寄生电容，UAB和UCD分别为变压器一次侧和二次侧的方波电压，RL为负载电阻，Co为输出滤波电容，i1为变压器一次侧谐振腔谐振电流，i2为变压器二次侧谐振腔谐振电流，im为励磁电感电流，C1和C2分别为一次侧和二次侧的谐振电容，L1和L2分别为一次侧和二次侧的谐振电感，Lm为励磁电感，n为变压器匝比。

图1 主电路拓扑Fig.1 Topology of main circuit

以正向运行为例，变换器存在2个谐振频率点，当仅有L1、C1参与电路谐振时，谐振频率为f1，若励磁电感Lm参与谐振，谐振频率为f2，具体表示为

根据开关频率的不同，可以分成3种工况：欠谐振工况(f2f1)，对应变换器增益M分别为：M>1、M=1、M<1。文献[11]对各种工况下CLLLC谐振型变换器的电路模态以及参数设计标准进行了详细分析。基于相关文献分析，给出变换器的等效电路如图2所示，图中i2=n(i1-im)。

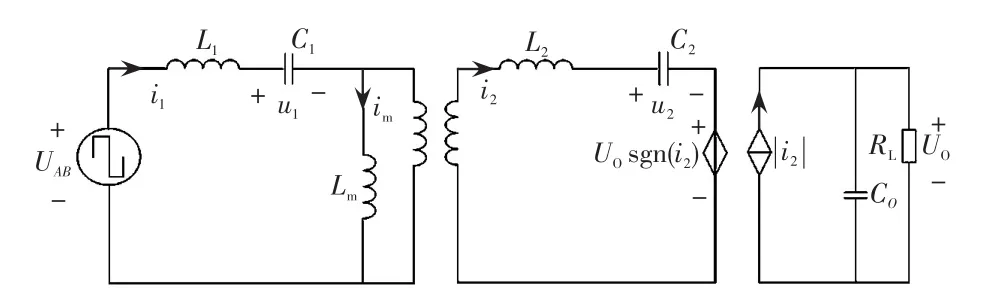
图2 CLLLC谐振变换器等效电路Fig.2 Equivalent circuit of CLLLC resonant converter

1.2 CLLLC谐振式变换器EDF建模分析

传统非隔离型DC/DC变换器通常采用状态平均法建立变换器模型，但由于隔离型高频DC/DC变换器的电路自然频率与开关频率接近，不满足状态空间平均建模方法所需的“小纹波假设”[12]。因此通常采用扩展描述函数方法EDF（extended describ⁃ing function）对隔离型高频DC/DC变换器建模。

1.3 CLLLC谐振变换器低阶等效模型

根据第1.2节的小信号模型分析，设定变换器的输入电压Uin为400 V，稳态工作频率fs设定为0.8f1，负载RL为24 Ω。变换器的拓扑参数如表1所示。

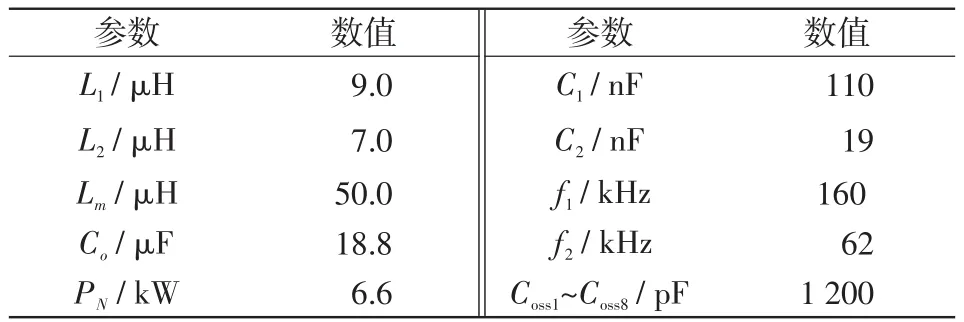
表1 变换器参数Tab.1 Parameters of converter

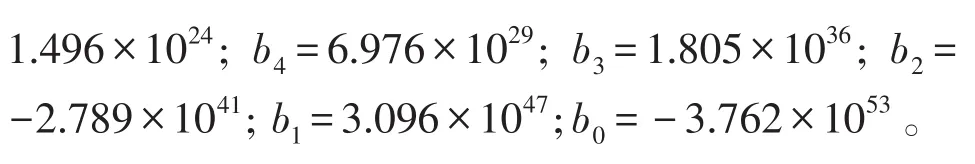
由式（5）可知，根据EDF方法建立的小信号模型是一个9阶的传递函数，这是因为在CLLLC谐振式变换器中存在多个无源元件，故小信号模型阶次较高。高阶次模型不利于控制器的设计以及环路的补偿，因此需要对变换器的小信号模型进行降阶处理，获得变换器的低阶等效模型。

扫频法是一种基于电路仿真软件的等效方法，能够快速给出功率变换器对应小信号扰动的伯德图，同时拟合出低阶等效模型，易于工程实现且具有较高精度。具体步骤为：在Matlab/Simulink环境中搭建CLLLC谐振式DC/DC变换器的功率模型，在变压器一次侧开关管的驱动信号频率即系统的控制输入端施加交流小信号扰动，设定扰动的幅值约为实际控制量的1/50，扰动频率则从20 Hz逐步增加到500 kHz，在测试点处测试输出电压响应扰动的幅值和相位增益，即可以根据扫频的数据结果拟合出系统的低阶等效模型。扫频基准频率可根据稳态工作点设定，本文以0.8f1为例。图3给出了EDF小信号模型、拟合低阶等效模型及扫频数据点的幅相特性曲线。对比可知，EDF小信号模型与MATLAB功率模型扫频拟合的低阶等效模型在数百kHz的高频段有误差，在低频段和中频段则有很高的拟合精度。在开关电源系统中，变换器的动静态特性主要由小信号模型幅相特性曲线的中频段和低频段决定，因此，低阶等效模型在数百kHz高频段的误差几乎不影响变换器的动静态性能[14]。

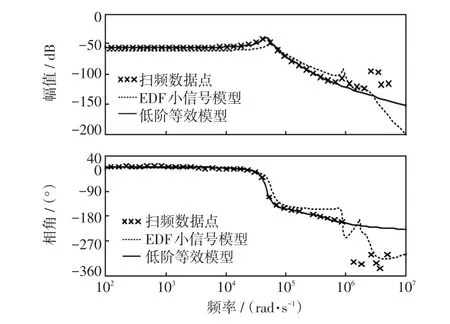
图3 模型幅相特性曲线(fs=0.8f1)Fig.3 Amplitude-phase characteristic curves of model(fs=0.8f1)

根据上述功率模型扫频的数据结果拟合的传递函数为

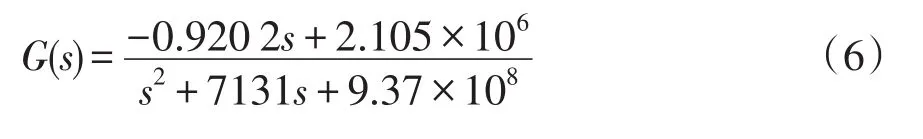
式（6）即可视为变换器在该稳态工作点的低阶等效模型。

2 广义预测控制器设计

基于低阶等效模型的CLLLC谐振式双向DC/DC变换器的广义预测控制系统架构如图4所示。

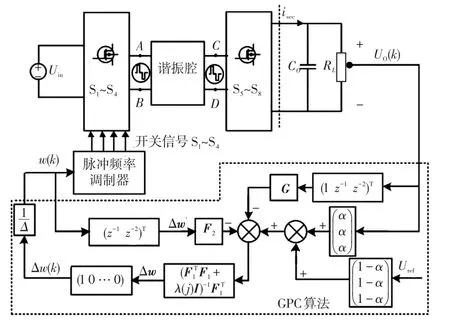
图4 基于低阶等效模型的广义预测电压控制系统架构Fig.4 GPVC system architecture based on low-order equivalent model

3 实验验证

为更加直观地验证上述GPVC策略的有效性，在6.6 kW双向CLLLC谐振式DC/DC变换器实验平台上分别实现传统电压PI闭环控制和本文所提出的GPVC策略，并设计多种实验工况进行对比分析。PI控制器参数根据文献[17]设计，补偿后的系统开环传递函数穿越频率为30 kHz，稳定裕度为50°。主控芯片采用TI DSP28377D双核数字信号处理器。实验平台如图5所示。

图5 实验平台Fig.5 Experimental platform

3.1 稳态性能对比实验

为了验证2种不同的控制策略下变换器输出电压的稳态特性，在输入电压为400 V、满负载工况下对比实验。实验结果如图6所示。

图6 CLLLC谐振变换器稳态性能验证结果Fig.6 Verification resuts of steady-state performance of CLLLC resonant converter

可以看出，2种控制策略均能够使变换器的输出电压达到设定的稳态输出电压。但是采用传统PI控制策略时，输出电压的纹波为2.1 V；而GPVC策略下，输出电压的纹波仅为670 mV，GPVC的静态误差明显小于PI，具有更好的稳态性能。

3.2 动态性能对比实验

为了验证2种不同的控制策略下变换器在输入电压突增或突减时输出电压的动态特性，针对输入电压突增或突减，在满载工况下分别设计对比实验。实验结果如图7和图8所示。

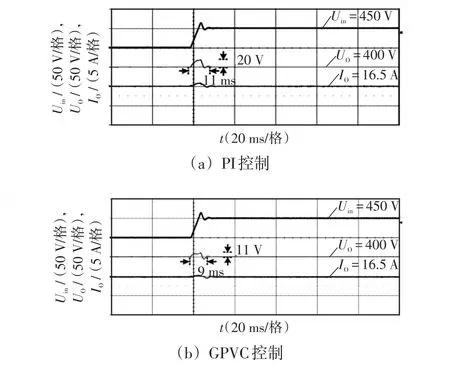
图7 输入电压突增时CLLLC谐振变换器动态性能验证Fig.7 Verification of dynamic performance of CLLLC resonant converter when input voltage increases abruptly

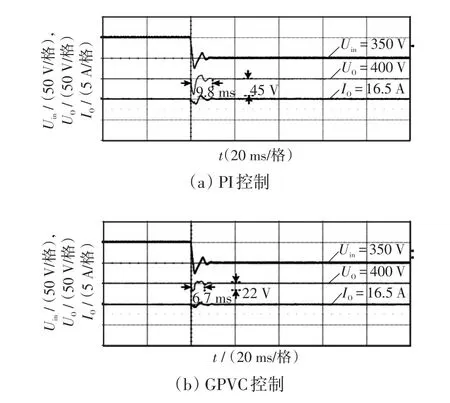
图8 输入电压突减时CLLLC谐振变换器动态性能验证Fig.8 Verification of dynamic performance of CLLLC resonant converter when input voltage decreases abruptly

由图7可见，当输入电压Uin由400 V突增至450 V时，传统的电压闭环PI控制下，变换器需要11 ms才能够调节输出电压到参考值，且输出电压波动值20 V；而在GPVC控制下，变换器恢复到参考电压的时间只需要9 ms；输出电压波动值仅为11 V。

由图8可见，当输入电压Uin由400 V突减至350 V时，传统的电压闭环PI控制下，变换器需要9.8 ms才能够调节输出电压到参考值，且输出电压的波动值为45 V；而在GPVC控制下，变换器恢复到参考电压的时间只需要6.7 ms；输出电压波动值仅为22 V。可以看出，相较于传统电压闭环PI控制，GPVC在系统输入电压突变时输出电压的波动值更小，并且具有更快的动态响应能力。

为了验证两种不同的控制策略下变换器在负载突变时输出电压的动态特性，针对负载的突增或突减，文中分别设计对比实验，实验结果如图9和图10所示。

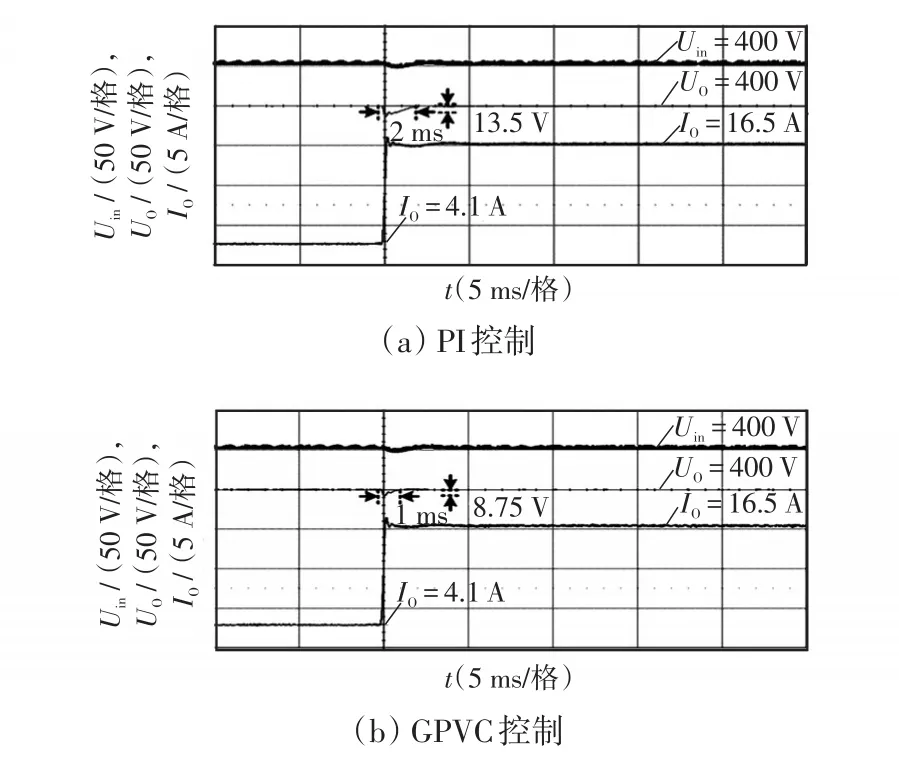
图9 25%负载突增满载时CLLLC谐振变换器动态性能验证Fig.9 Verification of dynamic performance of CLLLC resonant converter when load changes from 25%to 100%abruptly

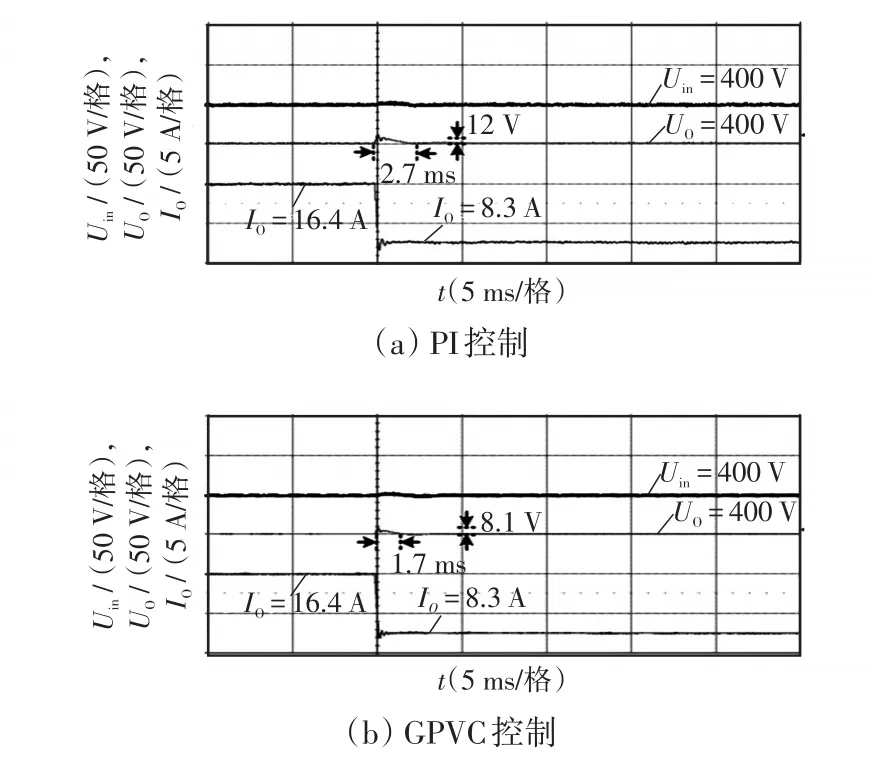
图10 满载突减半载时CLLLC谐振变换器动态性能验证Fig.10 Verification of dynamic performance of CLLLC resonant converter when load changes from 100%to 50%abruptly

由图9可见，当负载从25%突增至满载时，传统的电压闭环PI控制下，变换器需要2 ms才能够调节输出电压到参考值，且输出电压波动13.5 V；而在GPVC控制下，变换器恢复到参考电压的时间只需要1 ms；输出电压波动为8.75 V。

由图10可见，当负载由满载突减到半载时，传统的电压闭环PI控制下，变换器需要2.7 ms才能够调节输出电压到参考值，且输出电压波动12 V；而在GPVC控制下，变换器恢复到参考电压的时间只需要1.7 ms，输出电压波动为8.1 V。可以看出，当负载从25%负载突增至满载或从满载突减至半载时，GPVC策略下变换器输出电压的波动均明显小于传统电压闭环PI策略，在动态响应速度方面，GPVC策略也要优于传统电压闭环PI策略。

4 结语

本文针对CLLLC谐振式DC/DC变换器模型复杂、环路设计困难、动态特性慢等问题，提出一种了基于变换器低阶等效模型的广义预测控制电压控制算法，详细介绍了设计算法的理论推导和设计过程。主要贡献包括：拓展了预测控制在高频谐振变换器的应用，得到了优于PI控制器的动静态特性；使用扫频法简化了谐振变换器的预测控制器设计，易于工程实现。实验结果验证了本文所提控制策略的有效性，且相比于传统PI控制，GPVC算法不仅具有更好的稳态精度，而且在输入电压突变或负载突变工况下具有更优的动态性和鲁棒性。