基于聚类的差分进化算法的两阶段最优潮流方法

田 玮，江晓东

（天津大学电气自动化与信息工程学院，天津 300072）

在科学、工程和经济学等研究领域中，最优化问题比比皆是。最优潮流则是电力系统中典型的优化问题，半个世纪以来得到众多学者的研究[1-3]。针对由实际优化问题的复杂性导致传统优化算法难以求解到全局最优解的问题，研究人员通过对数学优化问题和生物进化之间潜在关系的观察，将自然的进化过程作为模型，提出了智能算法。近年来，智能算法的研究主要由进化算法和群体智能算法等组成[4-5]。由Storn和Price提出的差分进化DE（differen⁃tial evolution）算法是一种极具竞争力的进化算法[6]。相比其他进化算法，DE算法具有容易实现、进化效率高和鲁棒性强等优点，在被初级定义之时便广泛应用于科学研究与工程实践的领域[7-10]。同时，空间复杂度较低的DE算法具有一定的可扩展性以及处理大规模优化问题的潜力。目前，DE算法已经被拓展到多目标和有约束优化问题的研究领域[11-14]。然而，随着DE算法的实际应用，研究人员发现DE算法主要存在以下2个缺陷：第一，搜索停滞问题，即在种群进化后期，由个体间差异过小导致种群停止向全局最优解的方向进化的现象；第二，过早收敛问题，即种群个体多样性的缺失导致陷入局部最优解的现象。为了提高DE算法的性能以适应不同类型的优化问题，研究人员对DE算法的改进研究逐渐增多[15]，主要有：为DE算法结构增加组件，即以DE算法为进化框架，其他算法组件作为优化辅助[16]；修改DE算法本身，即算法结构的修改、搜索策略的改变、参数的选择等[17，18]以提高DE算法的性能。

为平衡求解最优化问题的速度和质量，本文在DE算法的基础之上，提出了一种基于聚类的DE算法的两阶段优化方法，简称两阶段优化方法，其中包含全局搜索阶段和局部优化阶段。两阶段优化方法的特点在于能实现确保求解最优化问题质量的同时提升求解速度，而这得益于第Ⅰ阶段的全局搜索中DE算法与聚类相结合，实现快速确定可能存在局部最优解的区域，以及第Ⅱ阶段的局部勘探中局部优化方法的采用实现高效收敛得到最优解。

1 基于聚类的差分进化优化算法

DE算法是一种并行直接搜索方法，其进化过程可概括为变异、交叉和选择3个部分。DE算法是通过个体之间的差分量实现个体的变异以及种群的进化的，具体表示为

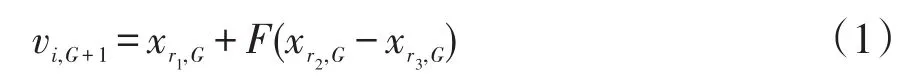
式中：i为索引；F为常数因子，F∈[0,2]，用于控制个体变异部分(xr2,G-xr3,G)；r1、r2、r3为随机选择且不同于索引i的整数，r1,r2,r3∈{1,2,…,NP}。因此个体的数目是必须大于或等于4以满足此条件。

DE算法在种群进化初期，所有个体之间的差异较大，交叉步骤有助于扰动参数向量的多样性的增加，而在种群进化后期，个体间的差分量逐渐减小，需要花费较多计算成本进行局部勘探。同时，控制参数以及进化策略的选择对DE算法后期的全局搜索能力影响大[19]。为提高DE算法搜索最优解的效率，本文提出了一种基于聚类的差分进化算法。

随着种群的进化，个体间的差分量逐渐减小，种群在搜索空间中会出现“群聚”的情况，即相似的个体聚集在可能包含局部最优解或全局最优解的区域。在文献[20]中提出对群聚的种群进行分组，并将种群分组数目不变和每个分组中的个体成员不变的状态称为“共识”。经过多次测试发现，在DE算法中，当种群达到共识状态时，全局搜索能力也开始退化。

因此，种群的共识状态可作为差分进化算法的停止条件，虽未求解到局部最优解，但可快速确定可能包含局部最优解或全局最优解的子区域。为检测种群的共识状态，本文采用一种无监督分类方法，即迭代自组织数据分析技术算法ISODATA（it⁃erative self-organizing data analysis technique algo⁃rithm）[21]，在种群进化过程中以固定的代数间隔对整个种群进行分组。ISODATA方法可在迭代过程中自动调整预先设定的聚类数量，以获得合理的聚类结果。基于聚类的DE算法，令随机种群进化达到共识状态时停止迭代，其具体的停止条件为：种群进化50代内分组的数目不变；限制目标函数（适应度）评估的最大次数为3.00×105。

2 局部优化阶段

局部优化阶段旨在第Ⅰ阶段锁定一个或多个存在局部最优解的子区域的基础上，用局部优化算法加速找到各子区域对应的局部最优解。在第Ⅰ阶段中，基于聚类的差分进化算法为非线性优化问题的解决提供了分组式的子种群；第Ⅱ阶段则从每个子群组中取最优的个体和中心点作为初点，利用局部优化方法收敛速度快的特性为每个子区域寻找相应的局部最优解，以提高解决优化问题的效率。

本文在该阶段选用的局部优化方法是拟牛顿法。拟牛顿法是一种基于逼近牛顿法的方法，其特点在于无需海森矩阵信息而是利用目标函数及其一阶导数构造出近似的目标函数曲率。因此，拟牛顿法具有收敛速度快和数值稳定的优点，也是所有利用一阶导数求解无约束优化方法中最有效的方法[22]。

全局搜索阶段和局部优化阶段共同组成两阶段优化方法，其具体流程如图1所示。本文将该两阶段优化的思想应用于电力系统的最优潮流计算。

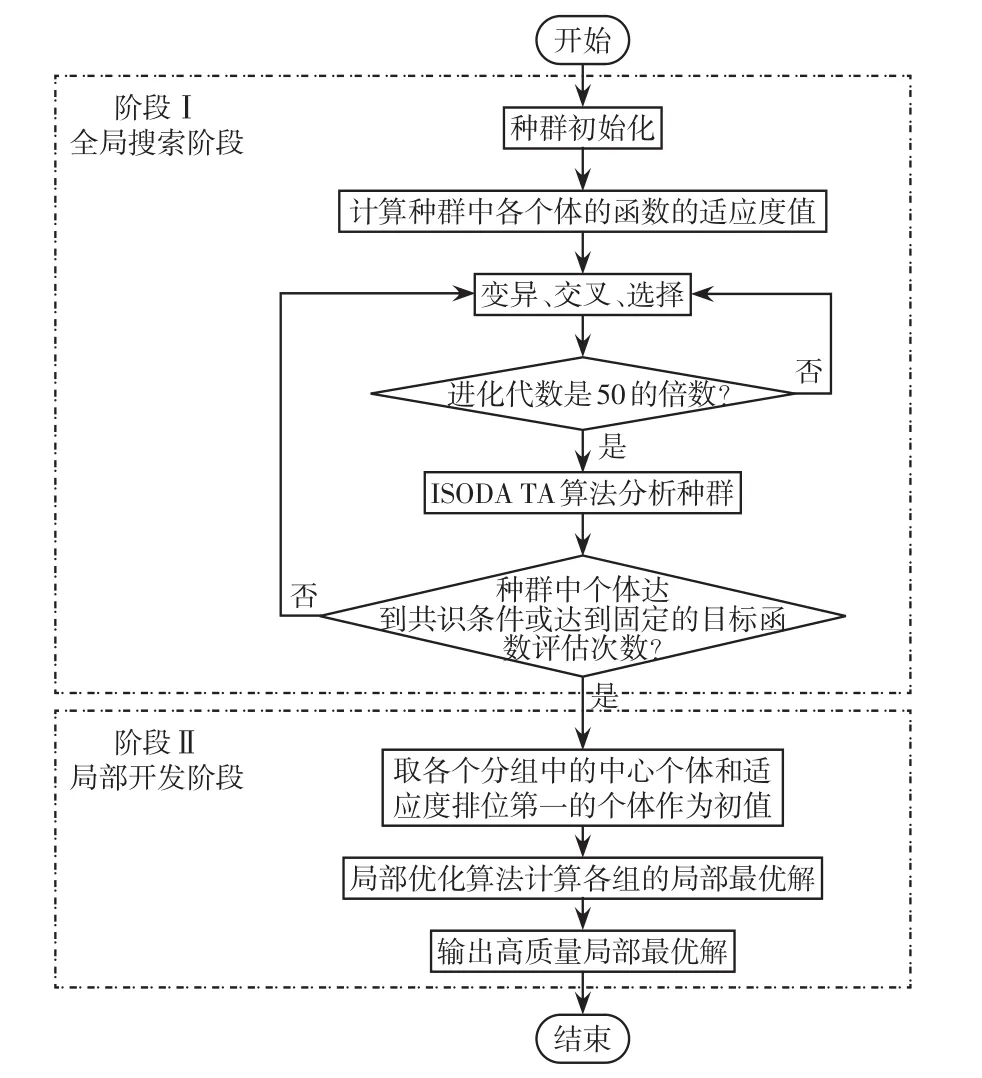
图1 基于共识差分进化的两阶段优化算法Fig.1 Two-stage optimization method based on DE

3 两阶段最优潮流方法

电力系统最优潮流是指在给定的系统结构参数和负荷情况下，优选满足系统运行和安全约束的系统控制变量，使系统的某一目标函数指标达到最优。从计算上，最优潮流问题是一个非线性规划问题，即一系列等式和不等式约束条件下的最小化问题，其数学模型可表示为

式中：u为控制变量，包括PV节点的有功功率输出和电压幅值、平衡节点的电压幅值、变压器分接头和可调并联电容器等；x为状态变量，包括全部节点的电压相角、PQ节点的电压幅值和发电机的无功功率输出等。其中，式（2）为系统的目标函数，一般为发电机燃料总费用、网络损耗或两者的组合，本文选用发电机燃料总费用作为目标函数；式（3）表示潮流方程等式约束；式（4）表示不等式约束，包括发电机有功和无功出力上下限、节点电压幅值的上下限和线路潮流的热极限约束。

两阶段最优潮流方法的详细流程介绍如下。

第Ⅰ阶段（全局搜索阶段）：基于聚类的DE算法中的种群个体变量是由控制变量和状态变量组成的，其个体的优劣评估指标是由最优潮流问题的转化得到，具体表示为

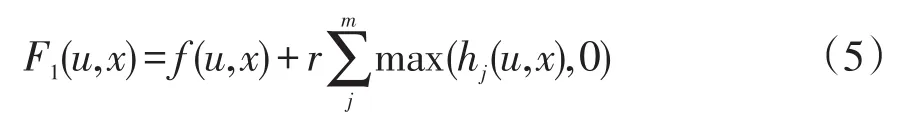
式中：r为不等式约束的惩罚参数，本文中r设置为100；m为不等式约束的数目。目标函数式（5）中不包含等式约束部分式（3），是由于在进化过程中，利用潮流计算获得当前控制变量下的状态变量x，可保证直接满足等式约束式（3）。

执行基于聚类的DE算法的具体步骤如下。

步骤1在已知的范围内，初始化随机种群。

步骤2计算种群中个体对应的目标函数式（5）。

步骤3利用式（1）对种群中的个体进行变异，其中参数F为0.7，并按照概率0.3进行交叉步骤；然后计算种群中个体对应的目标函数式（5），选择目标函数值小的个体进入下一步。

步骤4如果种群进化代数为50的倍数，执行步骤5；否则，执行步骤3。

步骤5ISODATA算法对种群进行聚类，如果执行聚类次数大于等于2，则执行步骤6，否则，执行步骤3。

步骤6检验种群的分组情况未发生变化，即达到共识状态，或计算目标函数次数达到规定次数，则执行第二阶段的优化；否则，执行步骤3。

第Ⅱ阶段（局部开发阶段）：在已确定的区域基础上，局部高效开发对应的最优解。在拟牛顿法中，需采用惩罚函数将最优潮流问题转化为无约束优化的形式，即

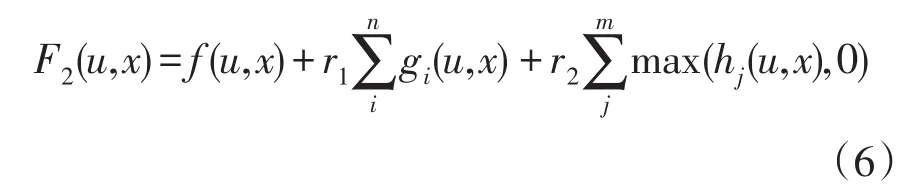
式中：r1为等式约束的惩罚参数；r2为不等式约束的惩罚参数；n为等式约束的数目。本文中r1和r2分别设置为1 000和10 000。

执行局部优化算法的具体步骤如下。

步骤1选取第Ⅰ阶段得到的每个分组中的中心位置和最优潮流目标函数式（2）最小的个体作为局部寻优的初值。

步骤2对每个初值采用BFGS算法，沿着由一阶导数信息构造的方向搜索局部最优解[23]。

步骤3从每个初值出发的搜索直至检验满足收敛判据停止，将搜索到的最优解组成最优潮流解集合。

步骤4输出最优潮流解集合中最优潮流目标函数（发电总成本）最小的潮流解。

4 算例分析

在一组基准非线性函数问题上对两阶段优化方法进行测试，验证其具备的有效性，并分析该方法在IEEE 118节点系统的最优潮流计算的结果，说明该方法的实用潜力。

4.1 基准函数测试

基准测试函数如表1所示，用于测试两阶段优化方法的性能，并与传统差分进化算法相比较，表中包含常规问题(f1)、旋转问题(f2-f3)、移位问题(f4-f6)和复合问题(f7-f9)[20]。在该算例中，变量维度为50以及随机选择的种群规模为30。DE算法的参数设置为：缩放因子F=0.7，交叉概率CR=0.3，差分策略DE/best/1。两阶段方法的第Ⅰ阶段中DE算法与上述参数设置相同，聚类步骤的间隔代数为50。

表1 测试函数Tab.1 Test functions

图2为测试函数f1（Rosenbrock）的等高线图，随机种群在第Ⅰ阶段中经过8 930次函数评估后，达到了共识的状态，即该种群被分为4个组且在进化间隔代数内保持不变；第Ⅱ阶段取每个分组中最好的（目标函数值最小）和中心位置的个体作为初点，利用拟牛顿法计算得到各子区域对应的局部最优解。图2中，“*”代表各组的中心点和“×”代表各组的最优个体，经局部优化算法计算后均收敛到全局最优解（1，1），即五角星处。

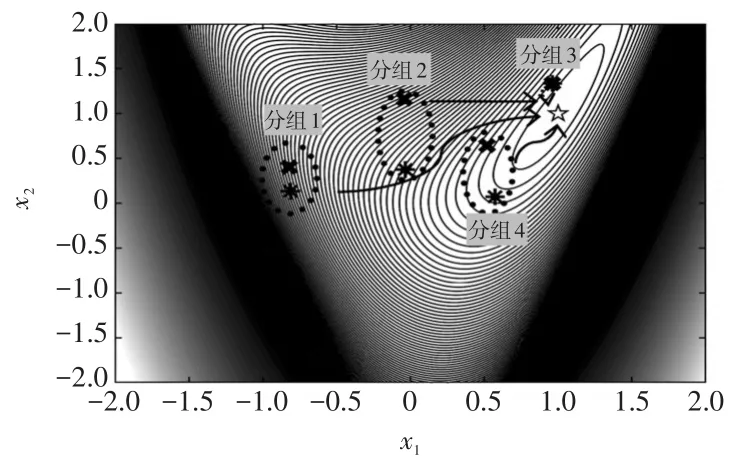
图2 测试函数Rosenbrock上的两阶段优化算法过程Fig.2 Process of two-stage optimization method on the test function Rosenbrock

为评估并比较两阶段优化方法和传统DE算法的求解质量和计算效率，表2统计了优化方法找到的最优解与已知的全局最优解的差值。

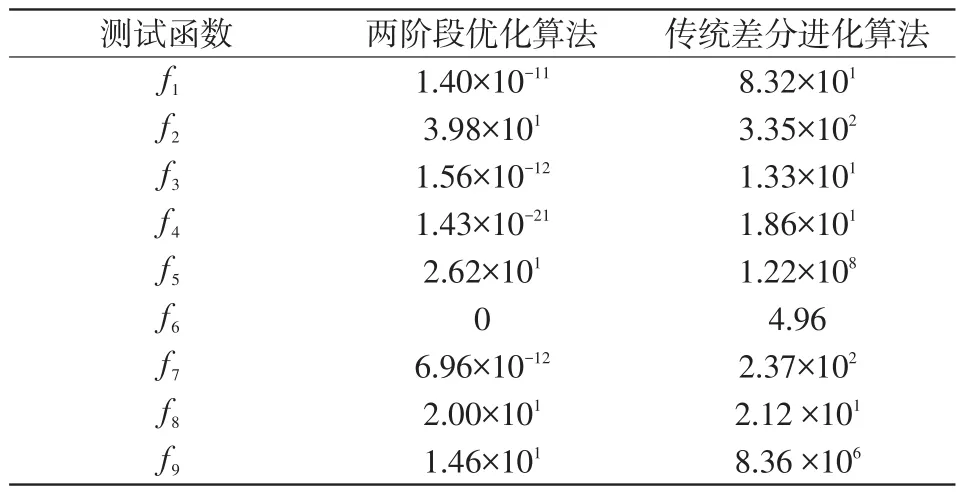
表2 两阶段优化方法与传统差分进化算法的优化结果比较Tab.2 Comparison of optimization result between twostage optimization method and traditional DE method

从表2可知，两阶段优化方法成功地找到了函数f6的全局最优解和函数f1、f3、f4和f7的接近全局最优解的解。而对于函数f2、f5、f9，两阶段优化方法虽然未找到对应的全局最优解，但大幅改善了找到的解的质量。上述结果验证了两阶段优化算法在寻找测试函数的全局最优解方面的有效性。

表3是优化过程中计算目标函数的统计总次数，其中Inf表示在规定的最大函数评估次数（3×105）内优化方法未找到全局最优解的情况。

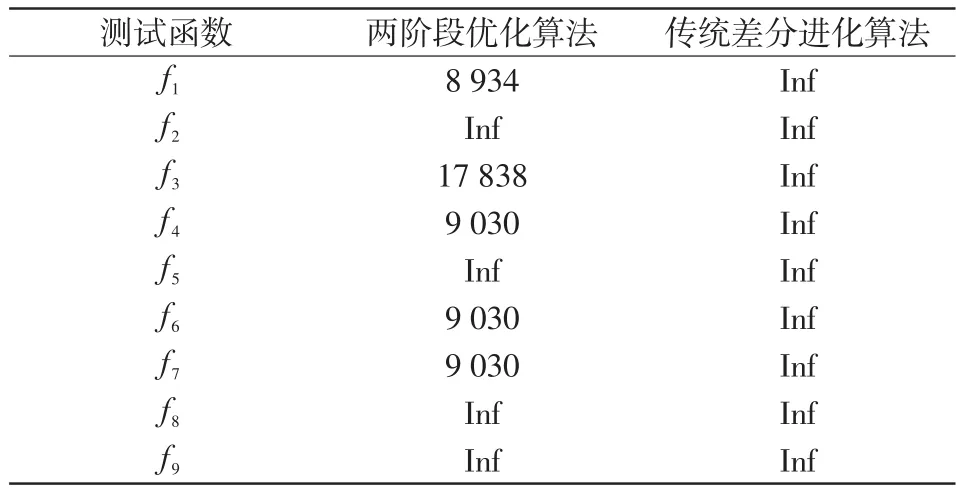
表3 两阶段法与传统差分进化算法的计算效率比较Tab.3 Comparison of computational efficiency between two-stage method and traditional DE method

由表3中的结果对比可知，两阶段优化方法寻找（近似）全局最优解的效率高。尤其在函数f1的求解中，两阶段优化方法函数计算仅花费8 934次便获取了高质量的最优解，约占设定最大函数评估次数的2.98%。上述实验结果表明，两阶段优化方法具有求解质量高和计算量小的优点。

4.2 最优潮流应用测试

本算例在MATPOWER的IEEE 118节点系统的最优潮流问题上对提出的两阶段优化潮流方法进行测试。具体的求解过程阐述如下。

第Ⅰ阶段中，基于聚类的差分进化算法中，种群规模设置为100，DE算法中参数设置与上述算例相同。状态变量中电压幅值的范围为[0.94，1.06]p.u.。随机初始化的总种群中最优个体对应的最优潮流目标函数（发电总成本）为135 856.50$/h（已知全局最优解的目标函数为129 660.69$/h）。经3 400次评估目标函数，种群达到共识状态，此时聚类得到4个分组。表4中列出每个分组的中心位置和最优个体对应的最优潮流目标函数值。由表4中可知，种群达到共识状态时，由聚类得到的4个分组的中心和最优个体的最优潮流目标函数相近。虽然基于聚类DE算法全局探索得到的个体最优潮流目标函数均大于随机初始种群中最优个体的，但是初始的随机种群中的最优个体不满足符合系统运行约束。

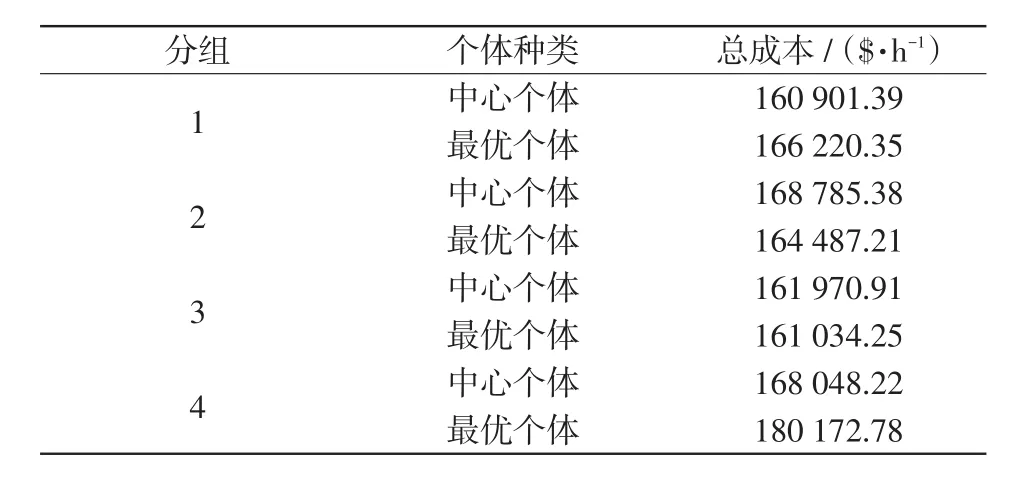
表4 基于聚类的差分进化算法计算结果Tab.4 Calculation result obtained by the group-based DE method

第Ⅱ阶段对各组种群的优质个体进行一步优化，即将各组挑选的优质个体作为初值，拟牛顿法从每个初值出发沿着梯度信息方向搜索得到对应的最优潮流解，如表5所示。

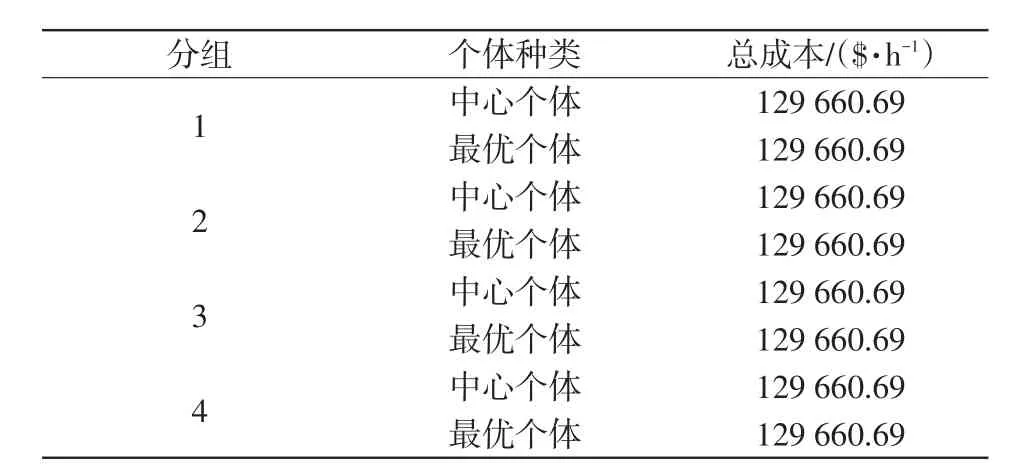
表5 局部优化算法计算结果Tab.5 Calculation result obtained by the local optimization method

由表5的结果可知，经拟牛顿法优化4个组均得到了全局最优解，这是由于第Ⅰ阶段提供的初值接近全局最优解，使得第Ⅱ阶段更容易地找到全局最优解。该测试结果验证了两阶段优化方法在电力系统最优潮流问题中的实用性。

5 结语

本文提出的两阶段优化方法结合了基于聚类的差分进化算法和局部优化算法，达到高效求解最优化问题的高质量局部最优解甚至全局最优解的目的。在两阶段优化方法中，基于聚类的差分进化算法提高了传统差分进化算法的搜索效率，实现快速确定包含局部最优解甚至全局最优解的区域；局部优化算法则用收敛速度快的优点弥补启发式算法进化后期效率低的缺陷。本文在一组基本测试函数以及不同规模电力系统的最优潮流问题上对提出的两阶段优化方法进行了测试，其结果表明，所提两阶段优化方法具有高效性以及应用于电力系统复杂非线性问题求解的潜力。随着电力系统的发展，最优潮流问题中离散变量的介入将使得智能混合优化算法具有一定应用的优势以及被进一步研究的意义。