事件和数据融合的加热炉煤气消耗量预测方法

刘书含，孙文强，2，范天骄，谢国威

（1.东北大学 冶金学院，沈阳 110819；2.东北大学 国家环境保护生态工业重点实验室，沈阳 110819；3.中钢集团 鞍山热能研究院有限公司，辽宁 鞍山 114044）

在钢铁企业中，高炉煤气、焦炉煤气和转炉煤气作为重要的二次能源，约占总能耗的30%［1］.然而，煤气消耗量受影响因素较多，难以准确预测，不同设备的煤气消耗量同样具有差异性，给能源综合管理带来弊端.加热炉作为典型的煤气消耗用户，其煤气消耗量约占轧钢生产能耗的76% ～80%［2］.然而，由于受到前后生产环节的制约和煤气管网压力的影响，加热炉生产波动较大，其煤气消耗量的精准预测一直较为困难，严重制约了加热炉的节能降耗及煤气系统智能管控的发展.因此，建立一种高性能的加热炉煤气消耗预测模型对煤气预测及智能化调度至关重要.

为了预测煤气消耗量，较为常用的方法是以先验知识为基础建立机理模型.郝晓静等［3］开发了高炉数据预处理软件，为高炉煤气消耗量的在线预测提供了有效方法.Sun等［4］考虑了煤气产生系数和消耗系数随产量非线性变化的情况，建立了钢铁企业副产煤气的机理预测模型.梁青艳等［5］考虑生产过程中影响加热炉煤气流量波动状况的静态及动态因素，建立了基于生产状态的分时段煤气消耗动态预测模型.虽然机理模型可以有效地分析影响煤气消耗量的因素，但加热炉的煤气消耗量受多种生产因素的干扰而波动较大，机理模型的预测结果难以满足实际需求.

随着计算机技术迅速发展，人工神经网络法、小波分析法等数据模型被应用于煤气消耗量预测.徐化岩等［6］依据小波分析方法、BP神经网络法、最小二乘支持向量机的性质建立了基于数据驱动的高炉煤气消耗量的复合预测模型.结果表明，数据模型在不同程度上存在滞后性.张琦等［7］采用灰色关联度分析了影响高炉煤气消耗量的因素，建立了高炉煤气BP神经网络预测模型，对高炉煤气的消耗量进行有效预测.聂秋平［8］将灰色理论与径向基函数神经网络进行组合，建立了基于灰色神经网络的煤气消耗预测模型.机理研究的不断深入和数据模型的不断发展为煤气消耗量预测提供新的思路.王彦辉［9］将机理模型和数据模型结合，提出煤气消耗量预测的理论构想.这种混合模型在高炉煤气产生量预测方面取得了较好的应用效果.Sun等［10］利用机理、数据和事件混合驱动的模型对高炉煤气的产生量进行了有效预测.赖茜等［11］对比分析了不同工况下回归分析法和人工神经网络法应用于高炉煤气产生量的预测效果.

为了更好地提高加热炉煤气消耗量的预测精度，本文对加热炉的操作事件进行了有效辨识，根据各事件对应的运行状态选择最佳数据模型，同时依托某钢铁联合企业加热炉生产过程的实际数据，建立融合事件和数据的混合预测模型，为钢厂能源智能管控提供理论和技术支持.

1 预测方法

1.1 差分自回归移动平均模型

差分自回归移动平均模型（ARIMA）［12］的模型本质是一个组合模型，由自回归项（AR）、差分项（Difference）和移动平均项（MA）三部分构成，如式（1）所示：

式中：VAR（p）为煤气消耗量的自回归项，p为自回归项数，该模型描述煤气消耗量当前值与历史值之间的关系，用煤气历史消耗数据对煤气的未来消耗数据进行预测；d为煤气消耗量的时间序列转变为平稳序列时所做的差分次数，用于提高煤气消耗数据的平稳性；VMA（q）为煤气消耗量的移动平均项，q为移动平均项数，该模型关注的是自回归模型中煤气消耗量误差项的累加.

ARIMA模型精度的关键是参数p，d，q的选定，意义在于将煤气消耗量数据的非平稳时间序列转化为平稳时间序列，然后将煤气消耗量对其自身的滞后值及对随机误差项的现值和滞后值进行回归，其预测方程可以表示为

式中：Vyt为煤气消耗量的预测值，m3／min；Vμ为常数项，m3／min；α为煤气消耗量的自相关系数；Vγt－1为自回归过程中煤气消耗量的前i阶多元线性函数值，m3／min；V∊t为煤气消耗量的误差值，m3／min；β为煤气消耗量的误差系数；V∊t－1为移动平均过程中煤气消耗量的前i阶多元线性函数值，m3／min.

1.2 人工神经网络模型

人工神经网络模型（ANN）［13－14］是近年来高速发展的一种深度学习方法，BP-ANN是一种多层的前馈神经网络，也是一种应用广泛的人工神经网络［15］，其结构如图1所示.ANN主要结构包含输入层、隐藏层和输出层，神经元只在相邻层之间实现全连接.该模型的原理是：煤气消耗信号由输入层神经元正向传播，经过网络训练输出预测值，得到的预测值由输出层向输入层反馈，将误差进行反向传播，从而逐步调整各个权值.常规三层ANN权值修正公式如下所示：

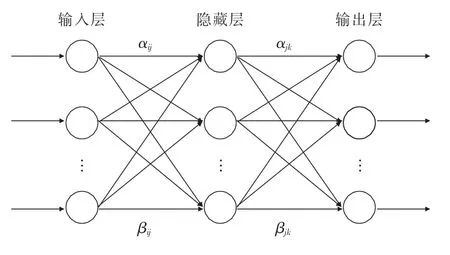
图1 煤气消耗量ANN拓扑结构图Fig.1 Topology of artificial neural network for predicting gas consumption

式中：E为网络预测输出的煤气消耗数据与实际输出煤气消耗数据之间的误差平方和；η为网络学习速率；αij为t时刻预测煤气消耗数据的输入层第i个神经元与隐含层第j个神经元的连接权值；αjk为t时刻预测煤气消耗数据的隐含层第j个神经元与输出层第k个神经元的连接阈值；βij（t）为t时刻预测煤气消耗数据的隐含层第i个神经元与输出层第j个神经元的连接阈值；βjk（t）为t时刻预测煤气消耗数据的隐含层第j个神经元与输出层第k个神经元的连接阈值．

1.3 混合驱动模型预测方法

加热炉的运行状态由标志性的操作事件决定，包含加热炉检修事件、加热炉待料事件.由此可将加热炉分为正常运行、停炉检修、待料运行三种运行状态.在预测加热炉的煤气消耗量时，首先应采集加热炉的操作事件，然后根据不同的操作事件确定加热炉的运行状态，选取与之相关的历史数据进行数据建模，完成对加热炉煤气消耗量的预测.在确定各状态对应的预测方法时，本文考虑了目前广泛使用的ARIMA模型和ANN模型.与单一预测方法相比，混合驱动模型预测效果更好.图2为混合驱动模型预测方法流程图.

图2 加热炉煤气消耗量混合预测方法流程图Fig.2 Flowchart of hybrid method for predicting gas consumption of reheating furnaces

1.4 误差评价

（1）平均绝对误差.平均绝对误差（MAE）表示煤气消耗量的预测值和煤气消耗量的真实值之间绝对误差的平均值，反映预测值误差的实际情况，表达式如下：

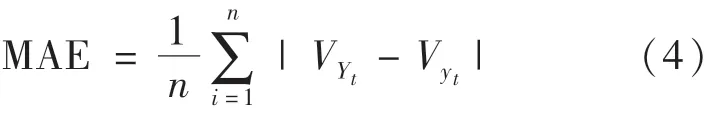
式中：VYt为t时刻煤气消耗量的真实值，m3／min；Vyt为t时刻煤气消耗量的预测值，m3／min.

（2）平均相对误差.平均相对误差（MAPE）表示煤气消耗量的预测值与真实值相对误差的绝对值的平均数，它具有下限（0），无上限，表达式如下：

（3）对称平均绝对误差.对称平均绝对误差（SMAPE）可以有效弥补有关煤气消耗量平均绝对误差在观测值为0时的缺陷，它具有下限（0）和上限（2），表达式如下：

2 结果与讨论

2.1 数据描述

本文采用某钢铁联合企业的加热炉高炉煤气消耗量数据，每5 min采样一次，试验中的数据采用2020年8月2日00：00至8月5日11：15实测的现场数据.时间序列包括1000 个样本（5 000 min）.ANN 模型中，第1～600个样本（0～3 000 min）作为训练集，第601～700个样本（3 005～3 500 min）作为验证集，第701～1 000个样本（3 505～5 000 min）作为测试集.煤气消耗量的时间序列如图3所示，表1列出了已知运行状态时间段.

表1 加热炉运行状态Table 1 Operational modes of the reheating furnace

图3 加热炉高炉煤气消耗量时间序列图Fig.3 Time series data of blast furnace gas consumption of the reheating furnace

2.2 ARIMA与ANN的比较

不同的时间段内ARIMA和ANN模型预测精度是未知的，因此有必要单独讨论加热炉不同运行状态下各模型的预测性能.

某段正常运行时期（4 700～4 840 min）的预测结果如图4（a）所示.结合表2可知，正常运行期加热炉高炉煤气的消耗量相对稳定.ARIMA模型的MAE，MAPE和SMAPE分别为1 055.39 m3／min，0.010 2和0.010 2，比ANN模型的MAE（1 712.30 m3／min），MAPE（0.016 6），SMAPE（0.016 7）低.由此可见，在正常运行期，ARIMA模型的性能优于ANN模型.

在加热炉运行过程中，由于自身故障或外部调试等因素，将出现停炉检修期；或由于生产限制，需保持空烧保温状态，将出现待料运行期.前者表现为随着时间的变化，煤气的消耗量逐渐降为0；后者表现为煤气消耗量逐渐降低（煤气消耗量不为0）而后逐渐上升至正常运行水平.停炉检修期因事件信号的迅速输入，可直接判断出煤气的消耗量；而在停炉检修期结束，煤气消耗量逐渐上升至正常运行水平（恢复期）的过程中，ARIMA模型泛化能力更强.在待料运行期，ANN模型可以更好地适应加热炉高炉煤气量的波动情况，滞后性较小.当预测数据在3 590～3 640 min时，加热炉处于停炉检修期，预测效果如图4（b）所示.此时ARIMA与ANN预测精度相同，均能够准确地预测煤气消耗量.随后在高炉煤气消耗量由0增长到120 000 m3／min的过程中，ANN与ARIMA预测都存在不同程度的滞后，但误差基本控制在2 000 m3／min以内.从表2中可以看出，ARIMA模型在停炉检修期（含恢复期）的MAE和SMAPE分别为441.23 m3／min和0.238 7，低于ANN模型的MAE（669.96 m3／min）和SMAPE（0.244 7）.由此可见，在停炉检修期（含恢复期），ARIMA模型表现出比ANN模型更好的性能.

表2 各运行状态下ARIMA和ANN的预测性能Table 2 Prediction performance of ARIMA and ANN models at each operational mode

图4 ARIMA和ANN模型在各运行期的预测结果Fig.4 Prediction of ARIMA and ANN models for each operational operation

图4（c）描述了待料运行期（4 490～4 640 min）的预测结果.由图可知，与ARIMA模型相比，ANN模型预测的效果更好.在4 500 min时，ARIMA和ANN都出现了滞后现象，ANN的预测结果在4 535 min时便可将平均绝对误差控制在4 000 m3／min以内，而ARIMA绝对误差始终高于4 000 m3／min，因此ARIMA的滞后现象较ANN更 为 严 重. ARIMA 模 型 的 MAE 为5 016.91 m3／min， 约 为 ANN 模 型（3 722.83 m3／min）的1.5倍；MAPE为0.101 4，接近ANN 模型的2倍（0.069 7）；SMAPE为0.100 4，比ANN模型高0.035 2.结果表明，在待料运行期，ANN模型可以较好地适应波动情况，而ARIMA存在的滞后性，预测效果比ANN模型差.

2.3 混合预测模型的性能

根据加热炉不同的操作事件选取不同的子模型建立混合预测模型.对图4（a）～（c）进行比较分析可知，在正常运行期ARIMA模型预测精度更高，在停炉检修期ARIMA模型依旧保持良好的性能，在待料运行期ANN模型的泛化能力更强.而混合驱动预测模型集成了加热炉不同运行状态下各模型的优势，对煤气消耗量进行准确预测，预测结果如图5所示.结果表明，该混合预测模型在加热炉不同运行期皆可表现出良好的预测性能.图6比较了ARIMA，ANN和混合模型的预测误差.由图可知，混合预测模型可以有效地提高预测的精度.ARIMA，ANN模型和混合模型的预测性能如表3所示.

图5 混合模型的预测结果Fig.5 Prediction of the hybrid model

图6 各模型的预测误差Fig.6 Prediction errors

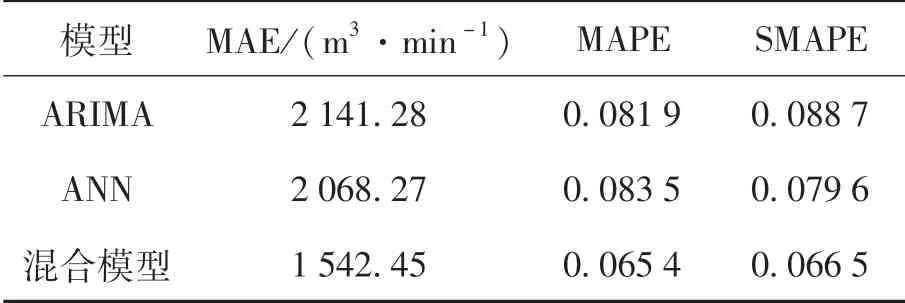
表3 各模型的总体预测性能Table 3 Prediction performance of all models for the whole period

从表3中可以看出，混合模型根据设备不同的操作事件采用不同的预测模型对煤气消耗量进行预测，因而较不区分事件的ARIMA和ANN模型更具有针对性.混合模型的MAE和SMAPE值分别为1 542.45 m3／min和0.066 5，模型优越性显著，这种差异得益于对运行事件的精准辨识以及与数据模型的高度融合，验证了事件和数据融合驱动下的混合预测模型的准确性及可行性.

3 结 论

（1）本文提出的融合事件和数据的加热炉煤气消耗量混合预测方法对加热炉操作事件进行了分类辨识，结合生产大数据对加热炉的高炉煤气消耗量进行了预测.利用筛选并处理后的1 000组加热炉高炉煤气消耗量数据，证实该方法预测性能好，滞后性小，实现了加热炉高炉煤气消耗量的精准预测.

（2）相比于ARIMA模型和ANN模型，混合预测模型的精确度更高.对于加热炉高炉煤气消耗量，混合预测方法的MAE为1 542.45 m3／min，小 于ARIMA （2 141.28 m3／min） 和ANN（2 068.27 m3／min）方法的MAE.混合预测方法的MAPE（0.065 4）和SMAPE（0.066 5）也分别低于ARIMA 方 法 的MAPE（0.081 9）和SMAPE（0.088 7），以及ANN方法的MAPE（0.083 5）和SMAPE（0.079 6）.