巧用题组模块，提升学生素养

邱秀兰

摘 要：题组模块，是指将数量关系相同、题型结构相似、解题思路类似或数学思想相近的题目，进行结构化设计，形成题组。基于题组模块的结构化呈现的课堂教学，以教师有结构地教，促进学生有关联地学，是引导学生指向对数学模式的感知、理解与建构的一个有章可循的方法。运用题组模块，有助于培养学生初步的数学建模能力，促进学生构建数学知识体系，提升学生数学思维水平，从而提升学生的数学素养。

关键词：题组模块 建模能力 知识体系 发展思维

题组模块，是指将数量关系相同、题型结构相似、解题思路类似或数学思想相近的题目，进行结构化设计，形成题组。在日常的数学课堂教学中，教师对例题或重难点内容的精细讲解往往以一种碎片化呈现，这样的学习内容，数学特征不够显著，不利于学生系统地学习。而将学习内容进行结构化设计，形成题组模块，能很好地突显学习内容的知识特征，能促进学生对数学知识的建构。

一、观察比较，培养学生数学建模能力

美国数学联合会前主席斯蒂恩指出：数学是关于模式的科学。运用题组模块能有效地提高学生数学建模的能力。“长方形的面积”是学生第一次接触几何圖形的面积计算，没有具体材料及对具体材料的有效探究，学生对长方形的面积计算无从下手，有些孩子可能已经知道了长方形面积公式，但只是知其然而不知其所以然。在课堂教学中，我尝试以题组模块的生成和变式为载体，通过对题组模块的观察、比较、验证与应用，让学生自主经历长方形的面积计算的建模过程，培养学生初步的数学建模能力。在教学中，首先让学生畅所欲言，说说自己对长方形面积计算方法的猜想，并说说自己的猜想依据；接着让学生根据导学提示自主探索、合作交流，观察汇总的记录表，说说自己的发现。

通过对列表中数据的观察、比较、讨论、交流，学生意识到长方形的长、宽决定长方形面积的大小，从而使学生对长方形的面积计算有了感性认识。紧接着，我让同桌合作，用1平方厘米的小正方形拼出一个18平方厘米的长方形。全班交流反馈后，学生发现尽管每组拼的形状有差别，长与宽也不尽相同，但长方形的面积都和相应长和宽的乘积相等。也就是，只要获得长方形的长和宽的数据，其面积大小自然可知。学生亲历了长方形的面积公式建模过程，印象深刻。

二、变式贯通，促进学生构建数学知识体系

数学知识具有系统性的特征，之前所学的知识往往对后面新知识的学习和理解起铺垫作用。在学习过程中，这种情形屡见不鲜：对某种题型，学生能完成基础的题目，但不能把所学知识融会贯通，对变式练习，没有清晰的解题思路。究其原因，首先是学生对知识点理解得不够透彻，其次是学生所获得的这些知识都是零散的、碎片化的，缺乏和其他知识点间的横向和纵向联系。故而，在数学教学中，教师要有意识地引领学生归纳出一些题型的共同特征，把相关联的题型系统化、网络化，构建一个完整的知识网络体系。在一个完整的知识体系中学习、理解知识，学生不仅对这个知识点理解透彻，还会加深对这个知识体系中其他相关知识点的理解。

人教版数学教材中的“行程问题”在教材编排上相对分散，教师在教学这类问题时，也基本上是跟着例题走，出现多少讲多少，点到为止，再遇到同类型的例题，依然按照之前的教学思路，让学生自主探究，费时费力。而将“行程问题”知识构建成一个完整的知识网络体系，形成题组模块，使学生能够主动应用已有的知识经验，自主解决同一题组里的相关联的问题，从而培养学生的迁移能力。

在教学人教版《数学》五年级上册“相遇问题”一课例题中，已知总路程、两人各自的速度以及时间，要解决“相遇时间”的问题。之前学生已经获得了“相遇问题”中求“总路程”的学习经验，故而，我先出示下题：美美每分钟走80米，天天每分钟走90米，星期六上午10时，两人分别从家相向而行，20分钟后两人相遇，两人家相距多少千米？通过唤醒学生已有的知识经验，学生重温相遇问题中的最基本的数量关系：总路程=美美走的路程+天天走的路程。随后，我引导学生对例题进行变式，将原题中的某个条件变成问题，尝试编题，形成题组。经过学生思考、交流，依次编出了求相遇时间（本课例题）、美美速度、天天速度三道题并得出三道方程式。进而引导学生发现，尽管问题不相同，但数量关系是相同的，可以将它们看成同一类题。进而再扩充题组，出现相向而行还未相遇、相遇又继续前行的题型，并探究其中的等量关系，最后组织学生观察、分析题组模块，发现题目千变万化，但数量关系是相同的，使学生透过形式走向实质，感受到它们的内在联系。再遇到类似的问题，学生就能做到触类旁通，提高了课堂学习效率。

三、逐层递进，提升学生数学思维水平

当前的数学学习活动，不仅要使学生获得学习、生活所必需的基础知识与基本技能，更重要的是要提高学生的思维能力，使学生成为一个富有创新能力的人。而数学课堂中练习活动也是学生获得基本知识和技能、培养能力、发展学生思维的重要途径。故而，教师要精心设计有层次性的练习，由浅入深、由单一到综合，了解各个知识之间的内在联系，铺设思维的“阶梯”，发展学生的思维能力。而题组模块正如一道“阶梯”，让学生拾阶而上，积极思考，循序渐进接近问题的本质，从而发展思维能力。

如在人教版《数学》五年级下册“长方体和正方体的认识”这一单元复习课上，教者设计了如下有阶梯式的题组：如下图，一个密闭的长方体玻璃容器，水深25cm。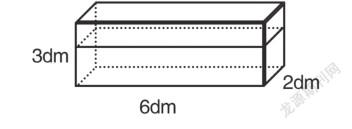

（1）这个长方体玻璃容器的表面积是多少平方分米？

（2）水的体积是多少立方厘米？

（3）将这个玻璃容器的右侧面放在桌面上，

①这时水深多少厘米？

②水与容器的接触面的面积是多少平方厘米？

第（1）（2）小题是基础练习，通过学生正确选择数据、计算长方体的表面积、水的体积，促进学生对长方体表面积和体积的基础知识和基本技能的掌握。第（3）小题的变式练习，求水深，既可以用“体积÷底面积”的方法，也可以根据两个底面大小关系来解题，右侧面是下底面的一半，所以高是原来的2倍。通过学生探究问题解决策略的过程，有效地发展了学生的思维能力，而求水与容器的接触面积，需要学生想象出水接触容器的每组面的大小，有利于培养学生的空间想象能力，从而提升学生的思维水平。

总之，基于题组模块的课堂教学，通过学生对题组的有序观察和分析，有效地培养学生的建模能力、归纳概括能力，提升学生思维水平，尝试用数学的思维探索问题、解决问题。基于题组模块的课堂教学，让学生走出杂乱无章的“题海”，学会练一组题，通一类题。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011版）[S].北京：北京师范大学出版社，2012.

[2]顾亚龙.题组模块：给数学课堂以生长的力量[J].小学数学教师，2019（1）.