综合考虑区段列车与直达列车的编组计划优化方法

林柏梁，张泽锡，王振宇

（北京交通大学 交通运输学院，北京 100044）

车流组织是铁路运输生产的重要环节，解决的核心问题是如何将车流变成列流。作为铁路运输工作组织中的主要内容，直达列车编组计划旨在确定哪些支点站间需要提供直达列车服务，在此基础上将车流按到站远近和运输性质组织到不同去向和不同种类的列车中，实现车流编组集结和中转滞留车小时的最小化。

国内外已在车流组织领域形成较为丰富的研究成果。Bodin等［1］将编组计划作为多商品网络流问题，构造了非线性混合整数规划模型，并采用启发式分解算法进行求解。Newton 等［2］将编组计划优化问题转变为服务网络设计问题，以支点站作为节点、编组去向作为弧，形成编组去向服务网络，并以所有车流在服务网络上产生的费用最小为目标，构造了线性混合整数规划模型。Ahuja等［3］构建了具有大规模、多商品和网络流等特点的模型，利用大规模邻域搜索算法，解决了包含数百万变量的列车编组计划问题。Lin等［4］为了解决中国实际路网的列车编组计划优化问题，建立了以所有车流集结和改编车小时最小为目标函数的双层规划模型，采用模拟退火算法求解并取得较好结果。Lin等［5］提出了车流径路和列车编组计划综合优化的非线性0-1 规划模型，代替了原有预先给定车流径路再进行编组计划优化的方法，并计算了由188 个支点站构成的铁路网、17 669 股非0 车流的超大规模案例。Chen 等［6］以中国铁路网为背景，提出了编组计划优化线性0-1 规划模型并通过树形分解算法求解，提高了求解效率。

在铁路车流组织问题的研究上，国内学者更倾向于按照问题属性进行分类研究［7］。朱松年等［8］较早提出同时考虑装车地直达列车编组计划与技术站直达列车编组计划的思想，构建了线性0-1 规划综合优化模型。林柏梁［9］从网络流和组合优化的观点出发，构建了基于直达列车和区段列车编组计划与车流运行径路整体优化的非线性0-1 整数规划模型。李文权等［10］首先阐述了空车调配问题对车站日常工作计划的意义，给出了基于车数最少的空车调配模型。纪丽君等［11］对点—弧模型和弧—路模型进行了改进，提出基于多商品流及车流不拆散原则下的车流分配和径路选择综合优化模型。刘晓伟等［12］采用动态车流组织的方式对编组方案进行调整，构建货物列车开行方案的整数规划模型，与静态模型相比，可以清晰体现车站线路时空能力的占用情况。

传统的货物列车编组计划优化方法［4-5，13-15］一般以相邻2 个支点站间必定开行区段列车（直通列车）的假设为前提，并默认相邻2 个支点站之间的区段车流均由区段列车进行运输。这对简化列车编组计划的优化模型是有利的。而在铁路运输实际生产中，当相邻2 个支点站之间的区段车流较小时，区段车流将并入摘挂车流通过摘挂列车进行输送。一般情况下，在完成整个路网的货物列车编组计划之前，相邻2 个支点站之间的区段车流是未知的，只有完成了整个路网的远程直达列车编组计划后，才会发现某些相邻2 个支点站之间存在区段车流过小的问题，这将导致该区段难以组织区段列车，先前假设无法成立、参数设定失真的情况。

本文从货物列车编组计划的整体性考虑，在车流径路确定的条件下改进原有的货物列车编组计划模型，在不预先假设相邻2 个支点站间必定开行区段列车情况下，分析摘挂列车与区段列车的组织特点，得到相邻2 个支点站间开行区段列车的临界车流条件；引入单位阶跃函数根据实际情况判断是否开行区段列车，构建无区段列车必开假设下车流组织优化的双层0-1 整数规划模型；采用基于模拟退火为主算法的迭代逼近策略，对改进模型进行求解；通过由京广铁路实际场景设计来的丰台西站—江村站通道案例，根据实际的车流大小和各站设备条件，确定需要编开直达列车的支点站以及编入已给定列车中的车流，实现车流集结和改编车小时消耗最小、路网性货物编组计划最优。

1 传统货物列车编组计划优化模型

在货物列车编组计划中，相邻2 个支点站（包括编组站或区段站）之间是否有必要提供区段列车服务，主要依据的是这2 个支点站之间的区段车流强度［16］。若要得出开行区段列车的车流条件，首先需对相邻2 个支点站之间的车流构成进行详细的分析。

1.1 相邻2个支点站的车流构成

定义车站i和车站j是2个相邻的支点站，在这2 个车站构成的区段上，有4 个中间站分别为a，b，c和d，则车站i到车站j区段内的车流构成如图1所示。图中：Dij为当整个路网直达列车编组计划完成后分配到此区段的区段车流；fia，fib，fic和fid分别为到该区段内对应中间站卸车的重车和分配到该区段内的空车，下角标字母表示发到车站，后同；faj，fbj，fcj和fdj分别为从该区段内对应中间站装车完成后去往车站j及以远的重车和调配到车站j及以远的空车。

图1 车站i到车站j区段内的车流构成

由图1 可知，区段内的摘挂车流是已知的，主要由在该区段内卸车的重车、分配到该区段内的空车、从该区段内装车完成后去往车站j及以远的重车和配送到车站j及以远的空车这4 部分组成；而整个路网分配到该区段上的区段车流，除从车站i到车站j（包括2 个车站相近区域）的短程区段车流已知外，其他都是不确定的。

换言之，区段车流的大小取决于整个路网上的直达列车编组计划，直到整个路网的列车编组计划编制完成后，才能得到各支点站之间的区段车流，再根据区段车流的大小，最终确定相邻支点站之间能否开行区段列车。然而，传统直达列车编组计划优化模型中，均未考虑区段车流的大小，这与铁路运输实际生产不符，因此有必要对传统的直达列车编组计划优化模型做进一步分析，从理论上探寻模型优化的空间。

1.2 传统直达列车编组计划优化模型存在的主要问题

传统的直达列车编组计划优化模型以车流的集结成本和改编成本之和最小为目标，其目标函数可表述为

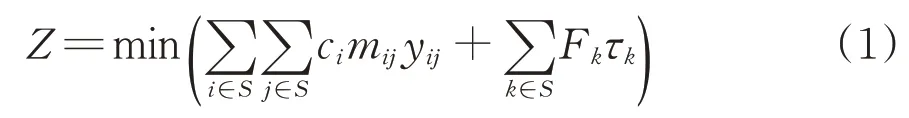
式中：S为路网中所有支点站的集合；ci为车站i的集结系数；mij为列车编组去向i→j的列车平均编成辆数；yij为0-1决策变量，当提供i→j的列车编组去向时取值为1，反之取值为0；Fk为编组站k的改编车流量；τk为每辆车在编组站k的改编成本。

按照铁路车流组织规律，从车站i到车站j的车流，若不直达到车站j的话，则必须搭乘某个近程列车在途中改编。即，存在如下唯一性约束

式中：xk ij为0-1决策变量，若车流在i→j的第1改编站为k且k≠j时，取值为1，反之取值为0；S-ij为除车站i和车站j外，i→j沿途的所有支点站集合。

若车站i和车站j为相邻的支点站，此时S-ij为1个空集，约束条件则变为

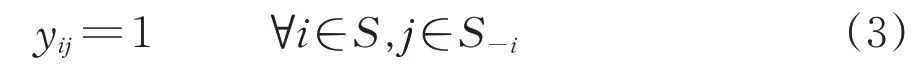
式中：S—i为与车站i相邻的支点站集合。

显然，传统的直达列车编组计划优化模型隐含了在相邻支点站间必定开行区段列车的假设。而在实际铁路运输中，当某些区段车流较小，不足以开行区段列车时，铁路部门一般只提供摘挂列车来满足相邻支点站之间货物运输需求。

1.3 区段列车的开行条件

为使理论优化结果更具指导意义，分别分析相邻2 个支点站间仅开行摘挂列车，以及既开行摘挂列车又开行区段列车这2 种情况下的车流条件，在总结区段车流与区段内摘挂车流关联特性的基础上，推导相邻支点站间开行区段列车的车流临界值。

1）相邻2个支点站间仅开行摘挂列车的情况

若某区段仅编开摘挂列车，则该摘挂列车所吸引的车流由以下3部分构成：

（1）车站i及其后方站所产生的，到达车站i和车站j间沿途各站的摘挂车流，即fia，fib，fic和fid。

（2）该区段内产生的，到达车站j及以远的摘挂车流，即faj，fbj，fcj和fdj。

（3）车站i及其后方站产生的，到达车站j及以远的区段车流Dij。

引入fLocalij表示i→j的摘挂车流强度，即

考虑到区段车流和摘挂车流均由摘挂列车携带，故该区段内这2 种车流产生的车小时消耗∆1为

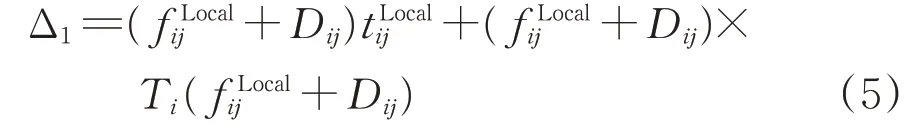
式中：为摘挂列车从i→j的运行时间；Ti（·）为与车流量相关的时间函数，表示在车站i开行摘挂列车时，摘挂列车在车站i的平均等待时间。

2）相邻2 个支点站间既开行摘挂列车又开行区段列车的情况

若车站i除编开到达车站j的摘挂列车以外，还编开到达车站j的区段列车，此时摘挂列车只吸引摘挂车流，原区段车流Dij将由区段列车运输，则该区段内这2 种车流共同产生的车小时消耗∆2为

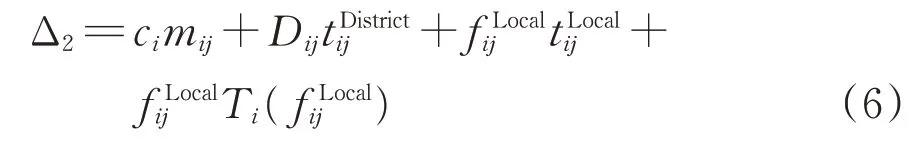
式中：cimij为编开i→j的区段列车时，所产生的集结车小时消耗；为区段列车在i→j的运行时间。

3）相邻2 个支点站间提供区段列车的临界车流标准

由式（5）和式（6）不难看出，相邻2 个支点站间开行区段列车的有利条件为Δ2<Δ1，即

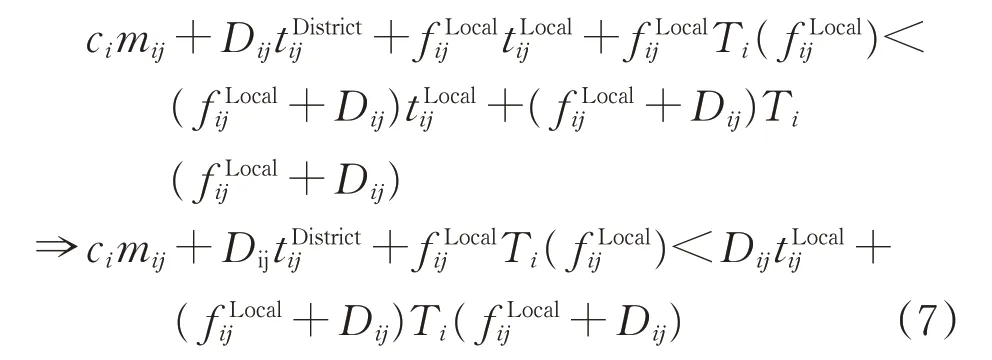
在区段车流较小的情况下，区段车流与摘挂车流的合并不会增加摘挂列车的对数，即

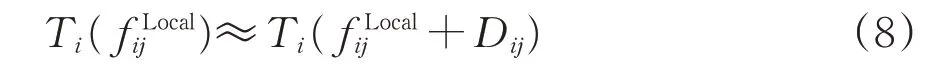
此时式（7）可进一步简化为

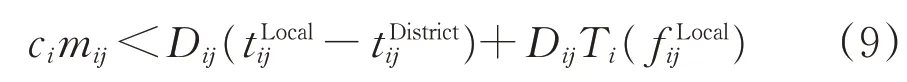
将式（9）整理变形，可得

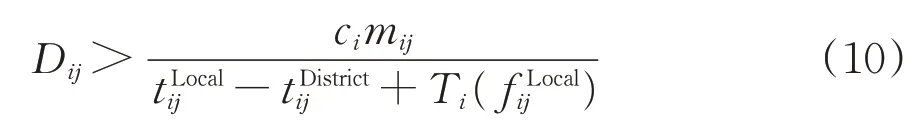
上式即为判断相邻2 个支点站间是否开行区段列车的条件。不难看出，摘挂列车在区段内运行时间（包含摘挂列车在途摘挂作业时间）越短，开行区段列车所需的区段车流Dij越大。

综上，相邻2 个支点站是否开行区段列车的车流临界值可以表示为

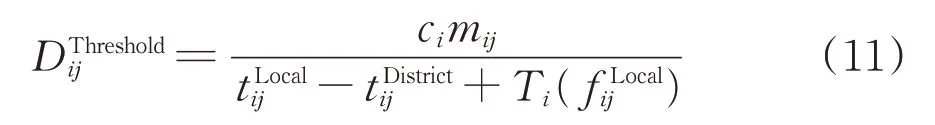
有了车流临界值后，通过引入单位阶跃函数，对传统的货物列车编组计划模型进行修正，避免了相邻支点站之间必然开行区段列车的假设。

2 无区段列车必开假设下车流组织优化的双层0-1整数规划模型

为使修正后的模型更符合铁路运营的实际情况，在考虑各个区段实际车流的基础上，提出在无区段列车必开假设下，可兼顾区段列车和直达列车开行方案的双层0-1 整数规划模型（简称改进模型）。其中，上层规划模型引入单位阶跃函数，根据实际情况判断是否开行区段列车，并确定哪些支点站间需要编开直达列车以及哪些车流编入已经给定的列车中；在此基础上，下层规划模型进一步确定每股车流的改编方案，最大限度地减少车辆改编作业次数，并计算得到单位车流的改编消耗。

2.1 上层规划模型——考虑最小区段车流临界值的列车方案优化

定义Rk为编组站k的有效改编能力；Hk为编组站k的可用调车线数量；为区段车流Dij由摘挂列车携带时每车增加的车小时消耗。同时定义下标l，s，n和u等也均指路网中的其他支点站。

根据式（11），判断区段车流Dij是否满足区段列车开行条件的单位阶跃函数ε(-Dij)为

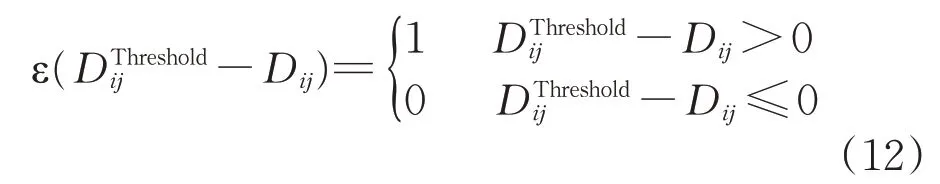
对于路网中的任意2 个支点站i和j，它们之间的车流量fij由2 部分构成，一部分为始发车流Nij，另外一部分是车站i的后方站s产生且在车站i进行改编到达车站j的车流。即

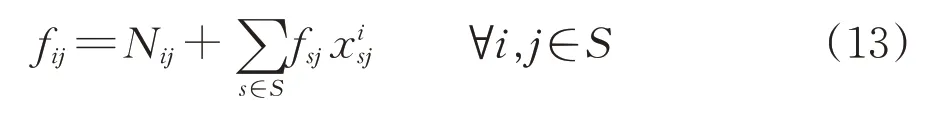
考虑到车流在编组站改编的不确定性，编组站k的改编量Fk作为1个决策变量的函数，可表述为

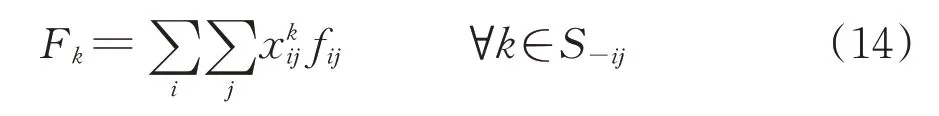
当铁路网上任意2 个支点站i和j提供1 个直达去向时，其可能吸引的车流量记为Dij（若车站i和车站j是相邻支点站则为区段车流），可表述为

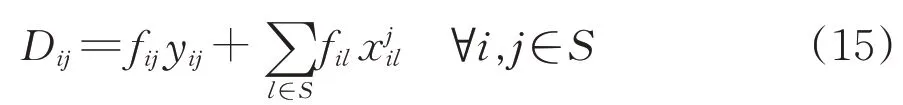
式中：第1项fij yij表示到车站j消失的车流；第2项表示到车站j以远消失的车流。

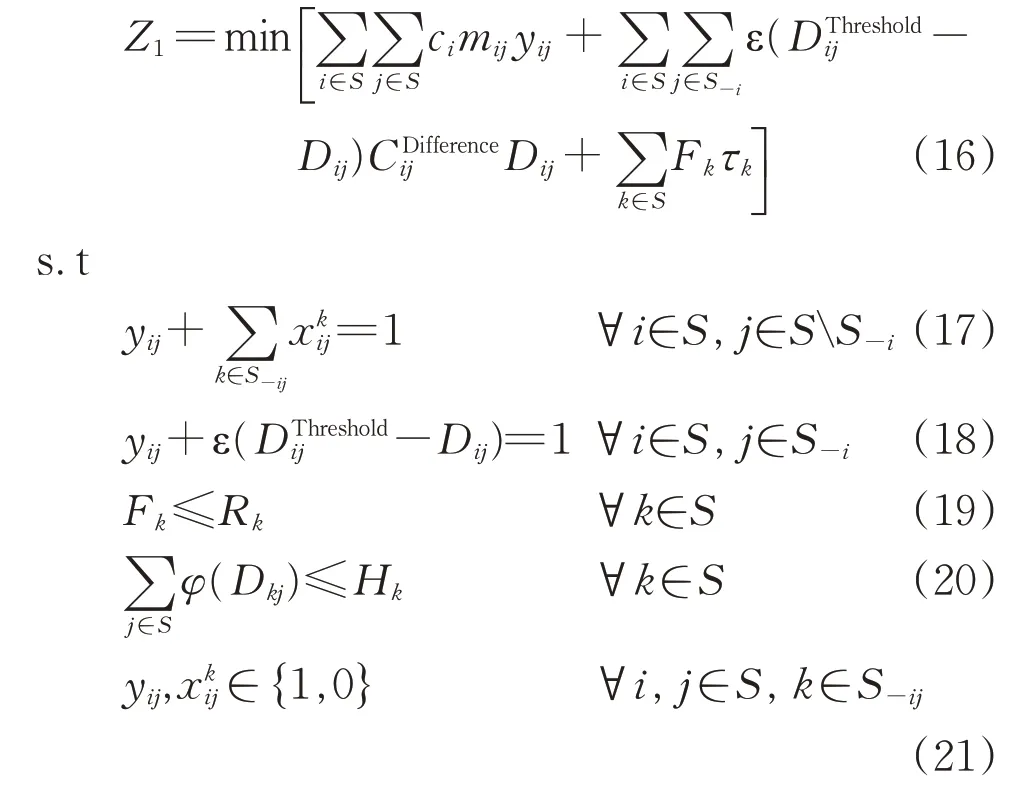
基于上述分析，综合考虑区段列车与直达列车的编组计划优化模型可表述为式中：φ(Dkj)为区段车流取Dkj时所占用的股道数，取表示日均车流量每增加200 就需要多占用1条股道，并采用向上取整的方式计算股道数［17］。

约束条件中，式（17）是唯一性约束，用于确保任一非相邻2 个支点站之间的技术车流采用或直达或改编的组织方式运输到目的地；式（18）用于判断区段车流量是否满足区段列车的开行条件，当区段车流小于临界值时，则ε(-Dij)=1，此时yij=0，表示i→j不开行区段列车；式（19）用于确保任一支点站的改编辆数不超过其有效的改编能力；式（20）用于确保改编车辆所占用的股道不超过任一支点站最大有效调车股道数；式（21）表示这2组变量均为0-1决策变量。

若相邻2 个支点站之间不开行区段列车，则相应区段车流将被摘挂列车所吸引，由于区段列车在途经2 个相邻支点站间的货运站均不会停留，而摘挂列车则需要在中途全部的货运站停留作业，因而区段列车的旅行时间明显小于摘挂列车的旅行时间。故当区段车流由摘挂列车运输时，会相应地增加车小时消耗。

2.2 下层规划模型——考虑改编成本最小化

定义dik为中间变量，表示当存在i→k直达列车服务时每车在编组站k的改编消耗，当不存在i→k列车服务时，dik取无穷大（在实际计算中取很大的整数M）。具体表达式为

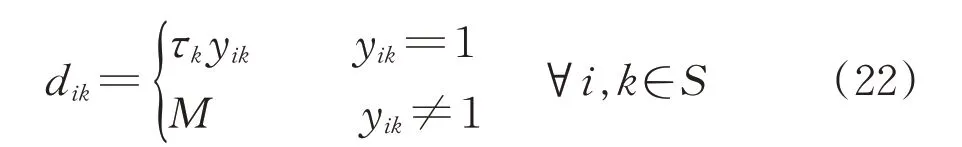
这样，在编组去向给定的情况下，确定每支车流的改编方案的下层规划模型为

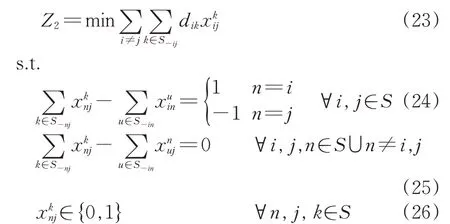
上述模型的目标函数是保证最少的改编作业成本。约束条件中，式（24）和式（25）都采用了流量平衡思想，其中式（24）为某股车流始发站和终到站的平衡约束，式（25）为某股车流中间站的平衡约束。式（26）表示该变量为0-1 决策变量，若车流在n→j的第1 改编站为k且k≠j时，取值为1，反之取值为0。

3 基于模拟退火为主算法的迭代逼近策略

基于模拟退火为主算法的迭代逼近策略为：首先假设所有相邻支点站之间均开行区段列车，采用模拟退火算法优化传统的直达列车编组计划模型，获得初步可行解；然后通过式（11）依次计算出各个区段之间开行区段列车的车流临界值；最后使用该临界值与实际分配到各个区段的车流进行对比，确定不满足开行区段列车的运行区段，再利用改进模型进行优化求解，通过反复迭代，得到改进模型的最优解，同时计算出总的车小时消耗。具体的迭代逼近策略流程图如图2所示。图中：FGenerate（·）为产生新解Xn+1的函数；FRandn（0,1）为在（0,1）的范围内产生的随机数；FUpdate（·）为退火算法温度更新的函数。

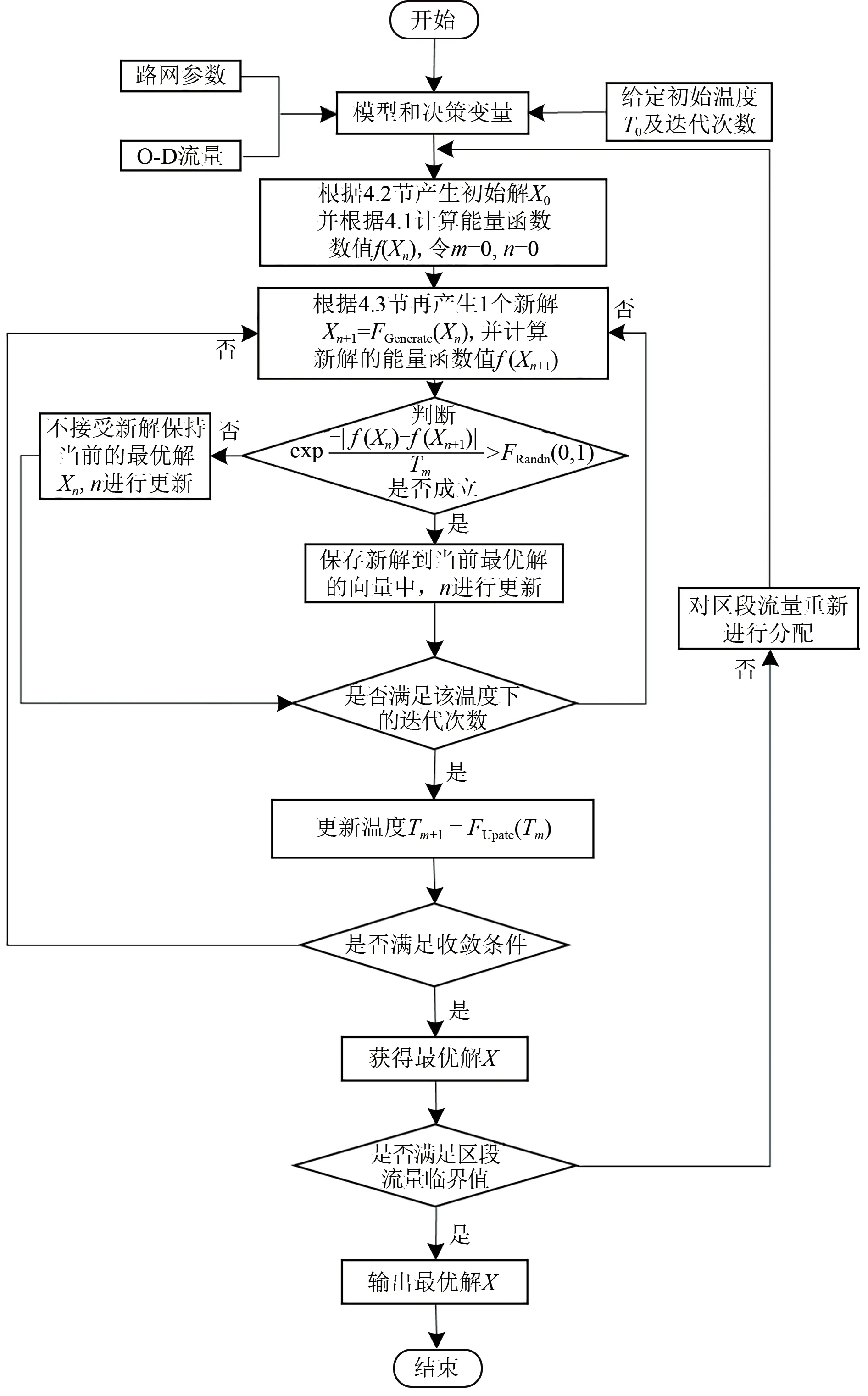
图2 基于模拟退火为主算法的迭代逼近策略流程图

1）能量函数

考虑到改进模型的复杂性，难以直接获得可行解，因此将复杂约束式（19）和式（20）作为惩罚项μ，即

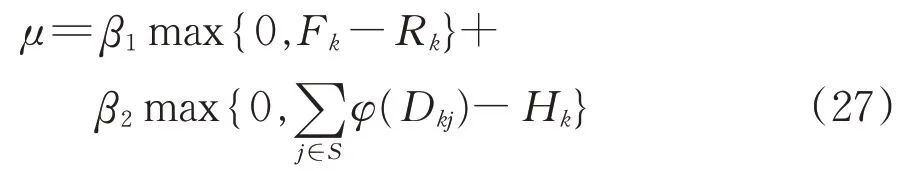
式中：β1和β2均为惩罚系数，根据实践经验以及相关文献［4］，分别取值为400和200。

然后，将改进模型的上层目标函数和惩罚项合并生成能量函数Z3为

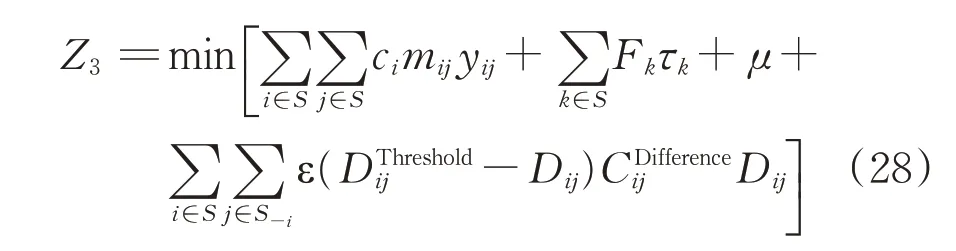
2）初始解

首先随机生成1 组满足约束条件式（17）和式（18）的初始解，其中yij可通过以下2 种方法直接产生：一是不管车流大小和去向远近，一律编入区段列车；二是不管各个去向的车流大小，一律开行到达终点站的直达列车。本文选择方法一，生成Y0=(…，yij，…)。

再根据下层模型求解对应的L0=(…，xk ij，…)，得到X'0=(Y0，L0)=(…，yij，…，xk ij，…)，作为模型的1 组初始解。最后将该初始解带入能量函数中，即可求得对应的能量函数值。

3）邻域解

定义集合Ωa来存放所有可能的开行去向、集合Ωb来存放当前解中已确定开行的直达去向，通过如下策略随机产生邻域解。

（1）从集合Ωa中随机选取1 个yij，若yij不在集合Ωb中，则令yij取值为1，并将其加入集合Ωb；若yij已经在集合Ωb中，则令yij取值为0，并将其从集合Ωb删除。

（2）按此方式，产生新解Ym，再采用与产生初始解相似的方法得到新解Xm=（…,xk ij,…,yij,…）。

（3）将新解带入能量函数，得到新的能量函数值，此时若能量函数值小于现存最优解，则接收该解；若大于现存最优解，则按照概率随机接收该解。

4 案例分析

京广铁路北起丰台西站、南至广州站，正线全长2 263 km。本文以该线路上的丰台西站、石家庄南站、郑州北站、武汉北站、株洲北站、衡阳北站和江村站这7 个主要编组站和1 个普通技术站邯郸南站为背景，着重分析邯郸南站—郑州北站通道中，当区段流不足以提供区段列车时，整个京广铁路上货物列车编组计划受到的影响。

为简化分析，在该区段内重点考虑8 个中间站，分别为马头站、磁县站、汤阴站、鹤壁站、淇县站、卫辉站、七里营站和焦作东站，相关的路网结构如图3所示。

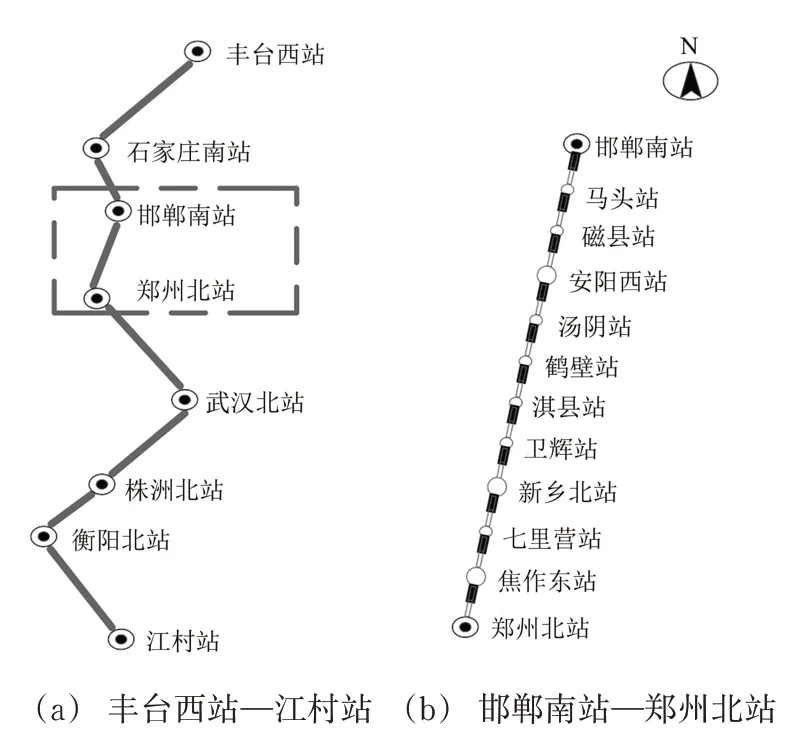
图3 路网结构示意图

4.1 数据准备

从铁路车流组织的角度分析，1 个支点站的主要参数包括集结系数、改编参数、改编能力、调车线数量等。其中集结系数、改编参数一般通过查定的方法确定，为不失一般性，本文采用文献［4］的参数值。

一般来说，支点站的调车线有数十条，改编能力可达数千车，由于重点研究如图3所示的局部网络，为说明问题，故假设剩余的改编能力和调车线数量见表1。

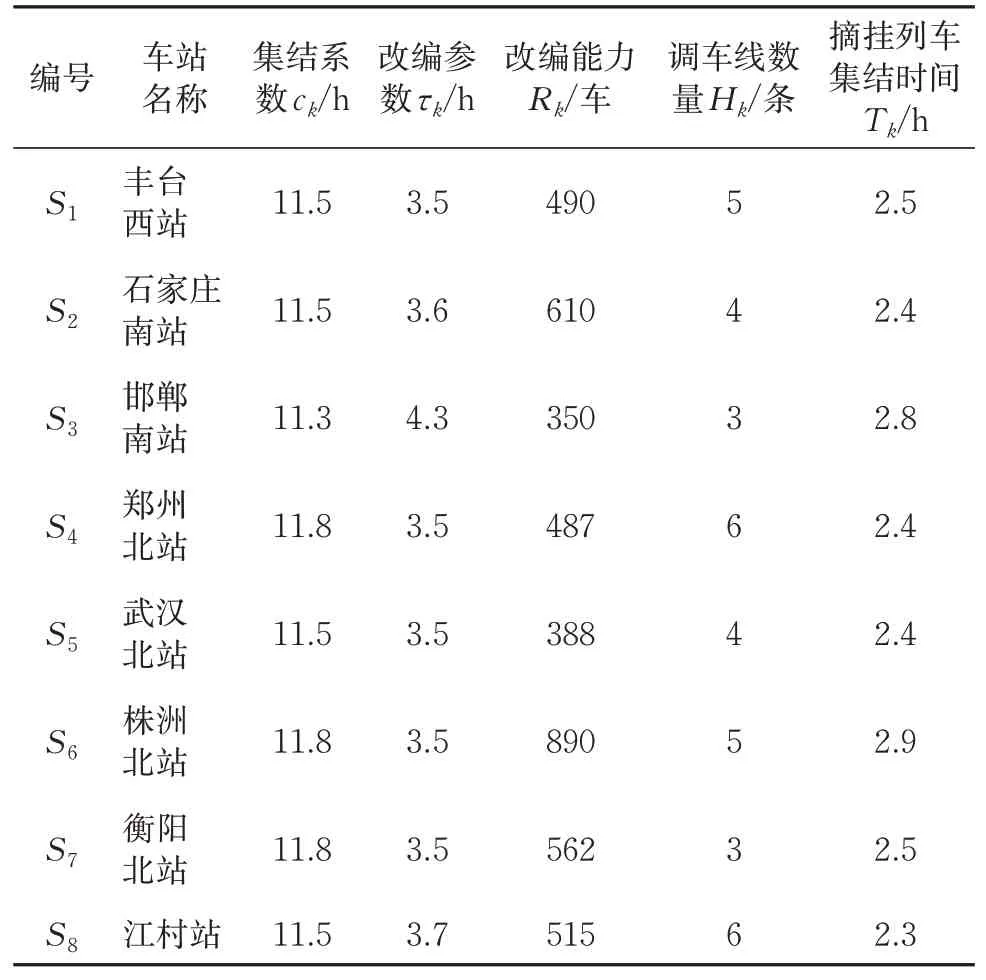
表1 沿途7个支点站的主要参数

各支点站间的摘挂车流相对固定，在区段车流较小的情况下，合并区段车流与摘挂车流并不会增加摘挂列车对数，因此将支点站k编发摘挂列车的平均每车集结时间简化为常数Tk。各个支点站之间的车流量见表2。

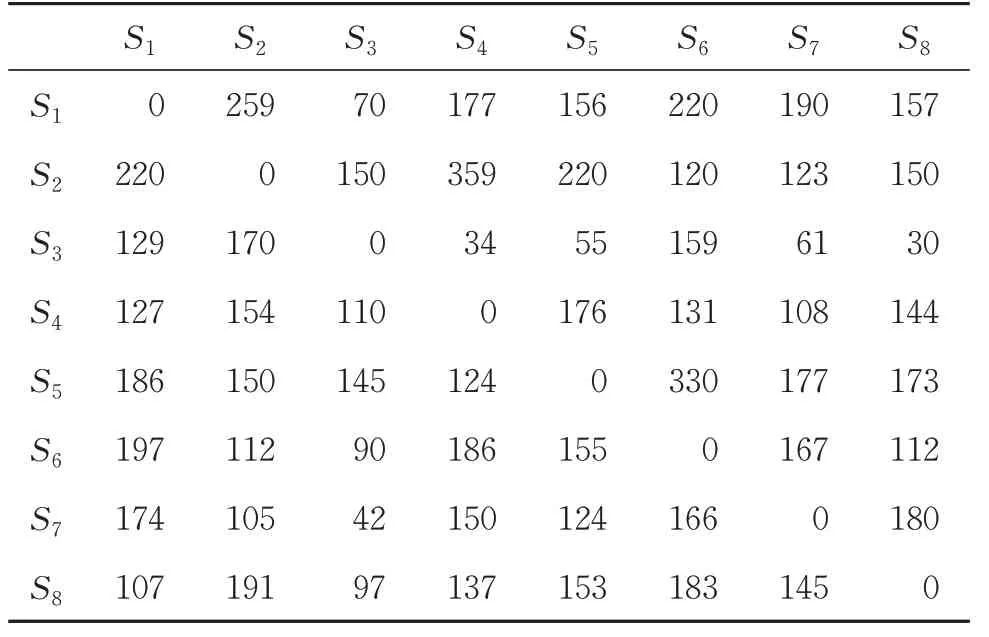
表2 支点站之间车流矩阵 车

本案例的各个区段的相关参数见表3。表中：tDistrict和tLocalij分别为开行区段列车和摘挂列车的旅行时间；DThreshold为根据式（11）计算得到该区段内开行区段列车的车流临界值。以表3中S1—S2对应区段下行方向为例进行分析可知，该区段为丰台西站—石家庄南站，区段内区段列车的开行时间为4.0 h，摘挂列车的开行时间为5.7 h，开行区段列车的车流临界值为150.60辆。

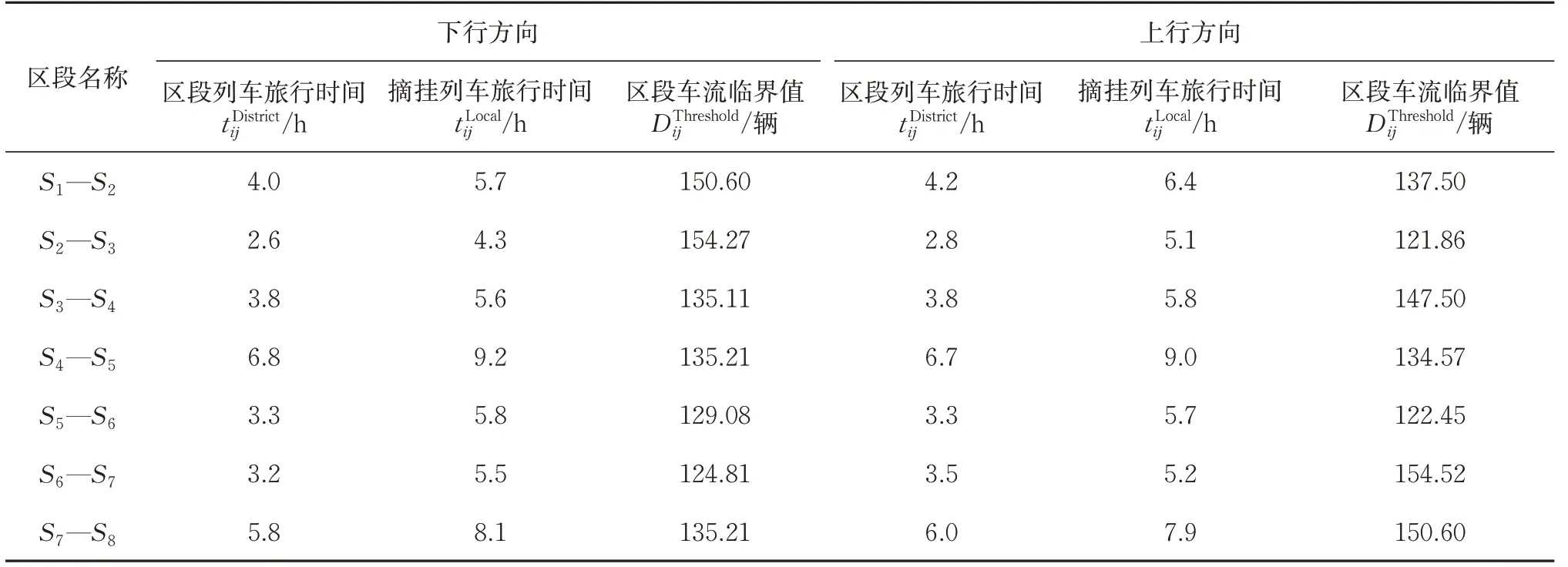
表3 相邻2个支点站之间管内列车的参数

4.2 基于传统假设的原模型技术直达优化方案

本案例的计算在Core 2.4 GHz 的PC 机上完成，共计获得编组去向33 个，其中相邻去向14个，直达去向19 个，总集结费用为21 016.6 车小时。所研究的90 支车流共产生改编车辆2 861 个，总改编费用为10 125.1 车小时。综合总改编费用和总集结费用，京广铁路的车流开行总成本为10 125.1+21 016.6=31 141.7车小时。

优化产生的33个编组去向分布如图4所示。图中：S1等节点表示京广铁路上对应的支点站（详见表1），非相邻支点站间的带箭头的弧线表示技术直达列车去向，带箭头红色弧线表示区段列车，其数值表示区段车流量。综合表3 与图4 不难看出：上行方向各区段的车流量均达到了开行区段列车的标准，无须进行调整；下行方向部分区段的区段车流小于开行区段列车的车流临界值；以S3→S4（邯郸南站→郑州北站）区段为例，传统模型计算得到该区段下行方向的车流量为119 辆，而开行区段列车的车流临界值为135.11 辆，显然，传统模型中无法考虑区段车流较小的情况，面对明显不利的方案，依旧会选择开行区段列车，这必然会造成能力浪费。

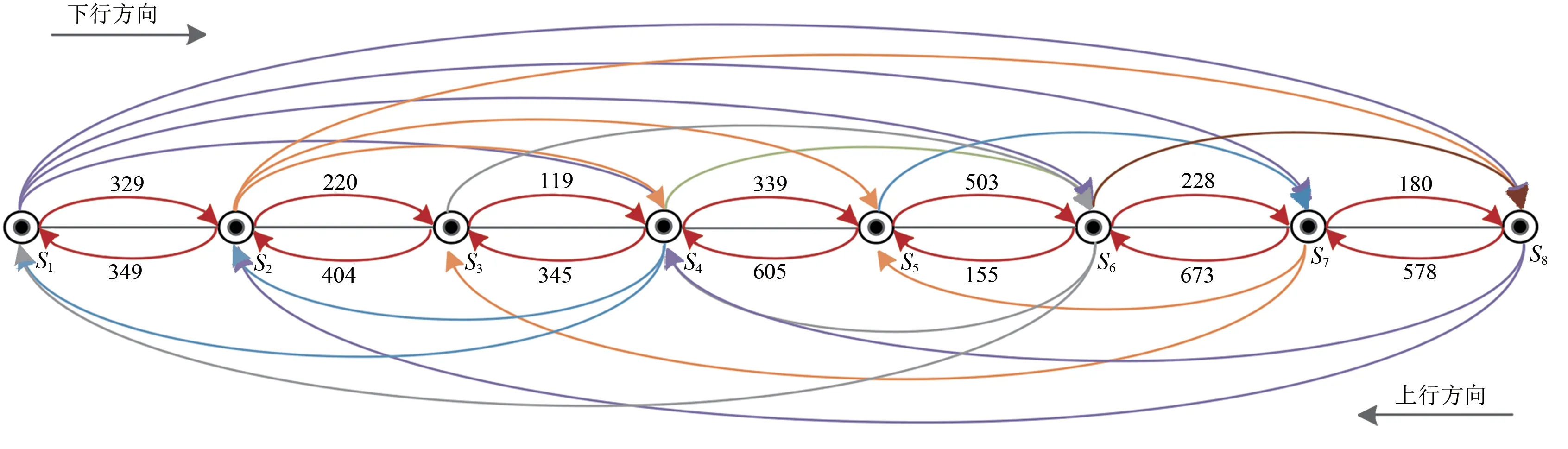
图4 基于传统模型假设的列车开行方案及区段车流

4.3 改进模型技术直达优化方案

根据上述分析，若开行S3→S4的区段列车，根据车流临界值，还缺少16.11 车。按照改进模型需要增加区段车流由摘挂列车携带的惩罚费用，此处CDifferenceij=4 h。利用迭代逼近策略进行重新计算，得到的新方案共获得编组去向37 个，其中相邻去向13个，直达去向23 个，停开区段列车1列，总集结费用为22 820.9 车小时。新方案共产生改编车辆2 194 个，总改编费用为7 911.6 车小时。车流开行总成本为7 911.6+2 2820.9+34×4=30 868.5车小时，与传统模型相比，改进模型计算得到的总成本降低了273.2 车小时。综合考虑直达列车与区段列车开行方案的具体编组计划见表4。

由于某些相邻支点间的区段车流量未达到开行区段列车的临界值，除该区段原有的短程始发车流改由摘挂列车运输外，其余区段车流将分摊到别的编组去向中，因此会对原有的直达列车编组计划产生影响。与原模型相比，改进模型计算出的总编组去向由33 个变为36 个，其中技术直达去向由19 个增加为23 个，停开区段列车1 列；改编费用显著下降，各区段车流也均符合开行条件，避免了区段车流不足仍开行区段列车的情况；区段车流由摘挂列车携带所增加的费用降到了最低，达到车小时消耗最小、路网性货物编组计划最优的目的。综合图4 和表4 可知，前例中邯郸南站→郑州北站的区段车流在原有区段车流不足的基础上继续下降至34车，该区段车流将通过摘挂列车运输。

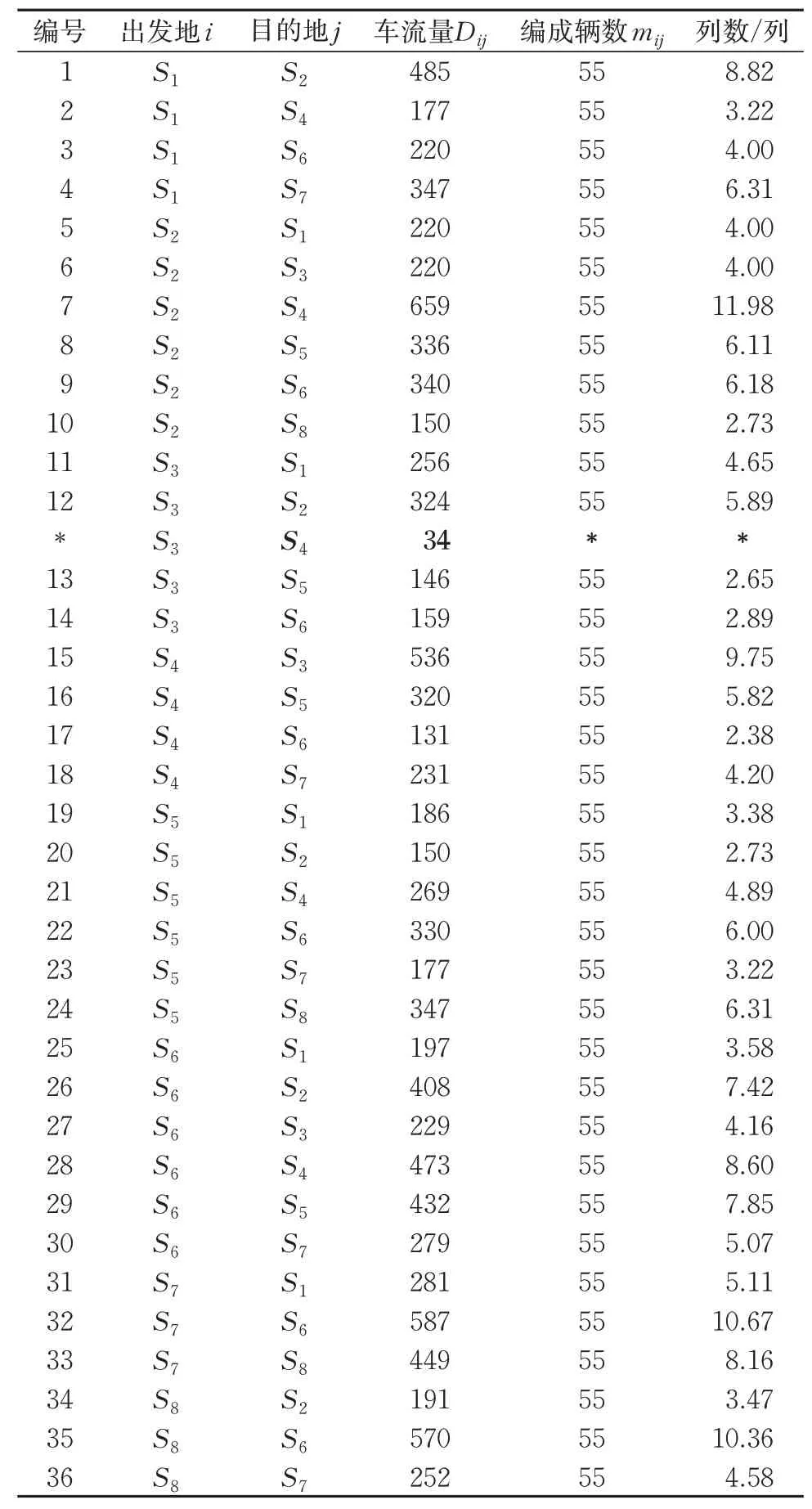
表4 编组去向及区段车流

5 结 语

本文从迭代优化的视角和货物列车编组计划的整体性入手，取消了相邻2 个支点站之间必定开行区段列车的假设，通过研究摘挂列车与区段列车的组织特点，确定相邻支点站间开行区段列车的临界车流条件；在无区段列车必开假设下，构建了包含非连续单位阶跃函数的车流组织优化双层0-1 整数规划模型，编组计划实现对区段列车与直达列车的兼顾；利用基于模拟退火为主算法的迭代逼近策略，通过基于京广铁路实际场景设计而来的丰台西站—江村站的通道案例，求解出新的编组去向及相应区段车流，得到的路网性货物编组计划更优于传统假设下的技术直达优化方案，这验证了将区段列车开行条件纳入远程直达列车编组计划综合优化的合理性。

本文研究基于车流径路已知的大前提，将车流径路融入直达货物列车编组计划的整体性研究，以及适用于全国路网的区段列车及直达货物列车编组计划的整体性研究，还有待进一步探讨。