基于DLP-WNN的高速铁路日客流量中期预测
魏堂建,杨星琪,徐光明,史 峰
(1.华东交通大学 交通运输与物流学院,江西 南昌 330013;2.华东交通大学 江西省高铁发展研究中心,江西 南昌 330013;3.中南大学 交通运输工程学院,湖南 长沙 410075;4.北京航空航天大学 经济管理学院,北京 100191)
高速铁路客流量预测能够为运营管理部门进行科学合理决策提供重要的数据支持,近些年来,客流量预测也一直都是相关学者和铁路运营管理部门的研究热点。在国外,TSAI 等[1]针对铁路客运短期需求预测问题,设计了多时间单元神经网络和并行集成神经网络对高铁客流进行预测;WEI等[2]结合经验模态分解和反向传播神经网络,设计了混合预测方法来进行短期地铁客流量预测;JIANG 等[3]结合集合经验模态分解和灰色支持向量机开发了短期客流预测混合模型,分别对短、中等和长距离高铁客流进行预测;BORJESSON[4]利用弹性系数法,结合高铁和航空实际数据,对长距离高铁客流进行了预测。在国内,王艳辉等[5]、汪健雄等[6]、刘辉等[7]分析提取历史特征数据,各自改进并分别建立了基于BP 神经网络的预测模型;汪志红等[8]针对春节假日在每年公历中不固定的特点,基于ARIMA 模型建立了月度季节调整模型预测春节期间铁路月度客运量;杨军等[9]利用小波分析技术并结合最小二乘支持向量机,进行了轨道交通短期客流量预测;姚恩建等[10]基于改进K近邻非参数回归方法,提出了城市轨道交通新站开通初期实时进出站客流量预测方法;腾靖等[11]考虑日期属性和天气因素,提出了基于PSO-LSTM 组合预测模型的城际铁路客运量预测方法;梁强升等[12]考虑城市轨道交通客流的时空交互关系,提除了1种融合循环门控单元和图卷积神经网络的城市轨道交通短时客流预测模型。上述研究的共性特征是,只针对短期客流量展开预测。
短期客流量预测基于过去若干期的历史真实客流量数据,利用某种方法预测下1期或者非常有限的若干期客流量,即输入若干期确定型历史数据,预测得到1 期/若干期客流量。根据具体时间单位的不同,预测期可以是年、月、日、小时、分钟甚至秒等时间单位,但不管在哪个时间单位下,其预测期数都非常有限。
然而,在实际高铁运输过程中,除了短期客流量预测之外,预测期数(天数)跨度范围更大的客流量预测同样具有重要应用价值。例如,当前铁路车票预售期通常为30 d,即当前至未来30 d的列车运行计划都已经确定,这意味着编制新的运输计划时,至少要考虑未来30 d的客流量波动情况。我国铁路一般会在每年春运、暑运的开始和结束等几个相对固定的时间点调整旅客列车运行图,也就是说,1 套列车运行计划的“服役”时间大概是3 个月左右。在这段时间内,因为工作日、周末、节假日及相关因素影响,高铁的日客流量会出现逐日波动,为使新制定的旅客列车开行方案和运行图等列车运行计划能适应市场需求,需提前对其“服役”时间内日客流量进行逐天预测。所以,更大预测期数(天数)下的日客流量中期预测就显得尤为必要。
不同于长期和短期预测,中期预测有其自身的特点和难点。与通常以年为预测单位的长期预测相比,由于高铁O-D 间的人口数量、GDP 总量以及土地利用情况等因素在中期时间范围内不太可能会有明显的变化,所以开展中期预测时无法比照长期客流量预测方法,利用上述宏观因素指标推演客流量的变化。与同样以天为预测单位的短期预测相比,中期预测的预测期数(天数)远多于前者,随着预测期数(天数)的推进,不可避免地需要在预测得到日客流量的基础上继续预测后续的日客流量,这将因误差累积而使后续预测精度显著下降,而这也是本论文将要解决的关键问题之一。
本文提出预测期天数为120 d 的高铁旅客日客流量中期预测方法,为高铁运营管理部门实际制定列车运行计划提供数据支持。从12306 铁路售票系统中提取高铁O-D 间的历史日客流量数据,在对这些历史数据进行特征分析的基础上进一步提取特征因素;根据特征因素设计日期标签和节假日标签,结合高铁日客流量的自回归特征,提出1种能够对高铁旅客日客流量进行中期预测的双层平行小波神经网络预测模型;通过算例分析测试模型的预测精度。
1 日客流量特征提取
选取京沪高铁北京至上海O-D对,从12306铁路售票系统中提取2014-01-01—2016-12-31 这3 a北京至上海所有日客流量,从非节假日和节假日这2个维度分析日客流量的特征。
1.1 非节假日的日客流量特征
2014—2016年北京至上海高铁日客流量如图1所示。由图1可以看出:以年为对比尺度,除个别日期的波动之外,3 a的日客流量在1 a内的起伏波动情况大致相当;以月为对比尺度,3 a 中相同月份的日客流量变化趋势较为一致,其中每1 a 1月和3月的日客流量都有明显增长趋势,而2月的波动都比较大,7月和8月都稳定在较高的数量状态,9月份相对8月份来说都有较为明显的回落趋势,11月份和12月份则有轻微的进一步下降趋势;以日为对比尺度,3 a 中具体到每1 a 的同1 d(例如每年第200 天),日客流量随着年份递进有逐渐增长的趋势,这说明日客流量存在以年为周期的波动特征。由此可以得到:年、月、日等日期属性对日客流量均存在周期性影响。
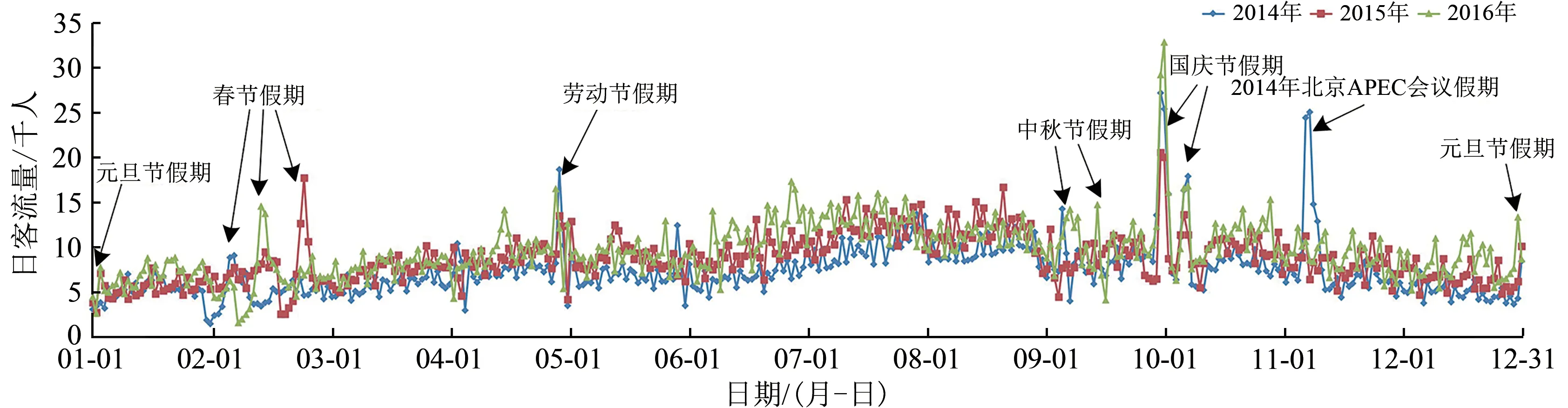
图1 2014—2016年北京至上海高铁日客流量
进一步地,分析每周内的日客流量特征。在我国,每1 a 的7月和8月由于没有其它法定节假日,该时段内每周的日客流量规律较易体现。选取2016年7—8月各周北京至上海日客流量进行分析,每周星期一至星期日的日客流量变化曲线如图2 所示。从图中可以看出:各周的日客流量波动趋势非常接近,均为星期一和星期二相对较低,星期三有小幅上涨,星期四出现回落,星期五可能因临近周末而出现上涨,星期六的日客流量相对较低,星期天又上涨。由此可以得到:星期信息对于高铁日客流量也具有周期性影响。
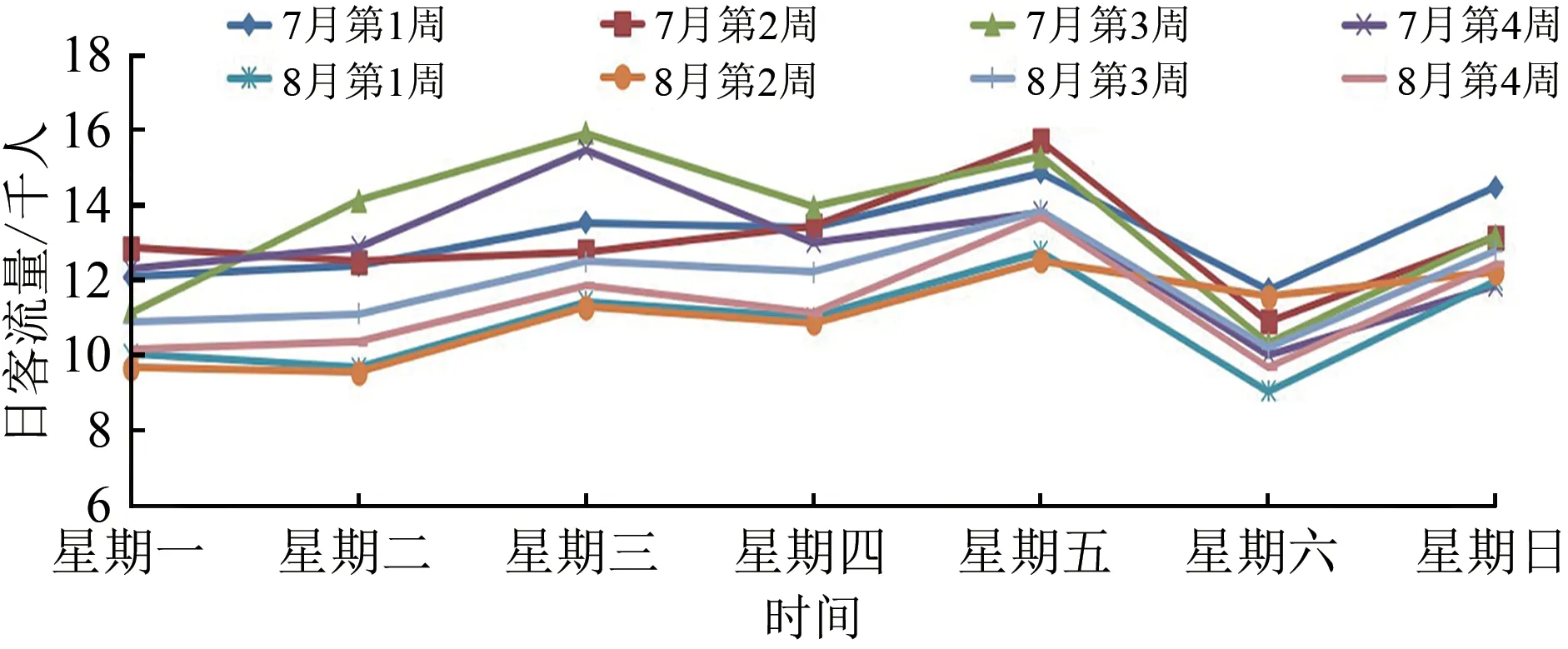
图2 2016年7—8月各周北京至上海高铁日客流量
1.2 日期标签设计
综上,年、月、日和星期这4 个日期因素对高铁日客流量有明显影响,而且它们会共同作用,影响日客流量在一定天数之内的变化。这种影响难以用简单的线性关系完全体现,换言之,将这些影响以计算式的形式完全体现并不容易;但同时,在进行中期高铁日客流量预测时,具体到预测期内的任意1 d,年、月、日和星期这4 个日期因素信息都是确定且可以提前获取的。因此,可设置“年”“月”“日”和“星期”这4 个日期标签对任意1 d进行标记,体现日客流量在年、月、日、星期不同尺度的动态周期变化特征,具体各个标签取值范围见表1。例如2014-05-01 是2014年的第121 天,同时是星期四,故其对应的“年”“月”“日”和“星期”标签的取值分别为2014,5,121和4。

表1 日期标签取值范围
显然,对于任意1 d,这4 个日期标签值都可直接获取,因此以日期标签作为确定型数据输入预测模型,并结合每1 d 的日客流量历史数据进行学习训练,可用于后续的预测。
1.3 节假日的日客流量特征
除了日常的动态周期性波动外,节假日对高铁客流影响也非常大,从图1可以看到,几乎所有日客流量波动较大的时间都是在节假日,因此,接下来进一步分析节假日的日客流量特征。
首先,每周的2 d 周末假日,对高铁客流量的影响具有较强的周期性。从图2 中可以发现:周末2 d 的假日不只影响其假日客流,对其紧邻星期五的日客流量也有影响;同时,处在2 d 假期中的具体第几天,日客流量也有明显差异。
除了常规的2 d 周末假日之外,还有元旦节、春节、清明节、端午节、劳动节、中秋节等法定节假日,并且通过周末调休形成连续的长假期。这些节日假期的具体统计信息见表2。由于节假日前后的日客流量也会受影响产生波动,因此选取节前2 d和节后1 d的日客流量一起进行分析。

表2 我国法定节假日统计
对于3 d假期,以劳动节和中秋节为例,2014—2016年北京至上海高铁日客流量分别如图3 和图4所示。由于2015年中秋节只调休成2 d 假日,假期长度与其它年份不一致,所以未一并分析。
从图3 和图4 可以看出:各年劳动节假期间的日客流量波动趋势大致相同,即在假期前第1天是高峰期,假期第1 天开始回落,假期第2 天是低谷,假期第3 天又上升,到假期后第1 天日客流量再回落;各年中秋节假期间的日客流量波动趋势也大致相同,前5 d 的变化趋势与劳动节非常接近,但最后1 d 不同,日客流量并没有下降而是继续上升。这说明尽管放假天数相同,但不同节假日类型对日客流量的影响存在差异。
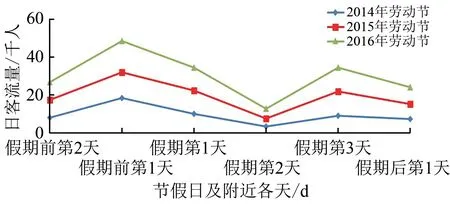
图3 2014—2016年劳动节假期北京至上海高铁日客流量

图4 2014—2016年中秋节假期北京至上海高铁日客流量
2014—2016年春节和国庆7 d 假期的北京至上海高铁日客流量分别如图5 和图6 所示。由这2 个图可以看出:对于同1个节假日,各年的高铁日客流量波动趋势非常接近;对于同一年,这2 个节日期间的高铁日客流量波动又有明显差异;对于春节假期,临近春节时,高铁日客流量会逐渐降低,春节假期的第1天高铁日客流量是极低的,然后逐渐回升,最高峰是在假期第7 天,假期后第1 天的日客流量略有降低;而对于国庆节,假期前1 d日客流量就明显开始暴涨,并在假期第1天形成客流高峰,随后会有1 个回落,在假期第3 天和第4 天形成低谷,接着在假期最后2 d 再出现1 个小高峰。这说明尽管同样是7 d 假期,但不同假期类型对高铁日客流量的影响也完全不同。
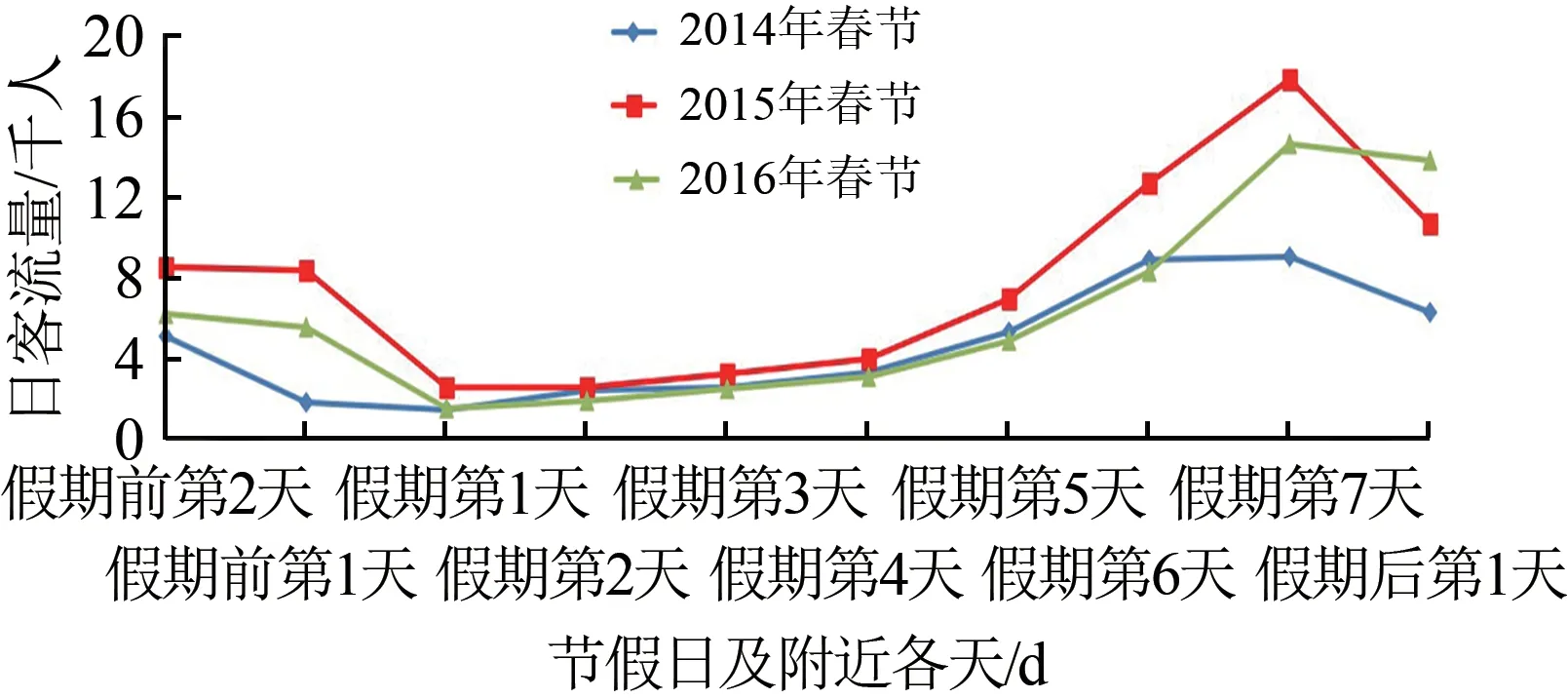
图5 2014—2016年春节假期北京至上海高铁日客流量
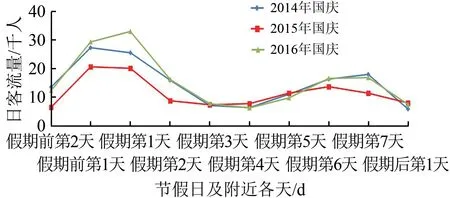
图6 2014—2016年国庆假期北京至上海高铁日客流量
通过以上分析,可归纳得到节假日对高铁日客流量影响具有如下特征:
(1)节假日天数不同,对高铁旅客日客流量的影响明显不同;
(2)节假日天数相同,同一节假日在不同年份对日客流量的影响较为接近;
(3)节假日天数相同,节假日类型对日客流量的影响存在差异;
(4)同一个节假日期间,各天的日客流量差异明显;
(5)节假日不仅影响自身各天的日客流量,还可能对假期前2 d、后1 d 的日客流量产生较大影响。
1.4 节假日标签设计
在对节假日的日客流量预测时,由于春节、清明、端午和中秋这4个农历传统节日,在每年的公历中并不是固定的日期,伴随而来的放假调休日期每年也并不相同,因此其对日客流量的影响很难直接从历史客流数据和日期信息中进行周期性捕捉,这就会对预测精度带来影响。但是,在实际进行120 d 的中期预测时,预测期各天是否有节假日、节假日类型和天数等信息是可以提前获知的,因此本文拟通过设置节假日标签来辅助提高客流预测精度。
上述特征(1)—特征(4)都是节假日对其自身的日客流量影响,因此设计“节假日天数”“该天数下的节假日类型”和“位于节假日第几天”这3个节假日标签,对每1 d进行标记;特征(5)体现的是节假日对其紧邻非节假日的日客流量影响,因此设计“节假日对附近影响”标签,来标识各种节假日对其前后1~2 d日客流量影响的程度。
记通过历史售票数据获得的任意第t天的高铁日客流量为̂(t),其客流变化率βt可由如下式(1)计算。

某节假日的时间范围为[t1,t2],令t=t1-1代入式(1),则可以得到该节假日前1 d,即(t1-1)d 的日客流量ŷ(t1-1)相对(t1-2)d 的日客流量̂(t1-2)的变化率βt1-1。
假设给定日客流量变化率的阈值为α。若变化率绝对值|βt1-1|≥α,则识别节假日[t1,t2]对其前1 d,即第(t1-1)天的日客流量产生了影响,且影响程度为βt1-1;否则,认为该假期对其前面各天的客流量不产生影响,并令βt1-1=0。
当|βt1-1|≥α时,即节假日[t1,t2]对其前1 d的日客流量产生影响的前提下,令t=t1-2,代入式(1)继续计算第(t1-2)天的日客流量变化率βt1-2。若|βt1-2|≥α,则识别该节假日对其前2 d的客流量的影响程度为βt1-2;否则,令βt1-2=0。
同理,令t=t2+1 代入式(1),可以计算得到节假日[t1,t2]的后1 d,即第(t2+1)天的客流量 变 化 率βt2+1。若|βt2+1|≥α,则 识 别 节 假日[t1,t2]对其后1 d日客流量的影响程度为βt2+1;否则,令βt2+1=0。
至此,可以计算所有节假日前2 d 和后1 d 的日客流量变化率,并将对应天的“节假日对附近影响”的标签值赋值为客流变化率β;而对于不属于节假日附近的其它各天,令其“节假日对附近影响”标签值为0。
于是,根据节假日对日客流量影响特征,设置的“节假日天数”“该天数下节假日类型”“位于节假日第几天”和“节假日对附近影响”这4个节假日标签及对应取值范围见表3。表中“该天数下节假日类型”标签的取值规则是:相同放假天数下,按照假期先后顺序依次对进行自然整数标号,例如元旦、清明、劳动、端午和中秋都是调休成3 d 假期的节日,因此“该天数下节假日类型”标签对应取值分别为1,2,3,4和5。另外,在个别年份存在元旦或端午节只放假1 d的情况,将这种1 d的假期都归为同一类型节假日;同样,中秋节也有2 d的假期情况,因此将这种情况的2 d 假期和周末假期视为同一类型节假日。
按照表3 就可以对每年中任意1 d 进行节假日标记。例如,5月1日是劳动节3 d 假期的第1 天,劳动节属于3 d 假期下的第3 类,且是节假日内部而不属于节假日附近,于是该天的节假日标签“节假日天数”“该天数下节假日类型”“位于节假日第几天”和“节假日对附近影响”的取值依次为3,3,1 和0。在进行日客流量中期预测时,预测期各天的节假日标签可以提前标定,作为确定的数据输入到预测模型中。
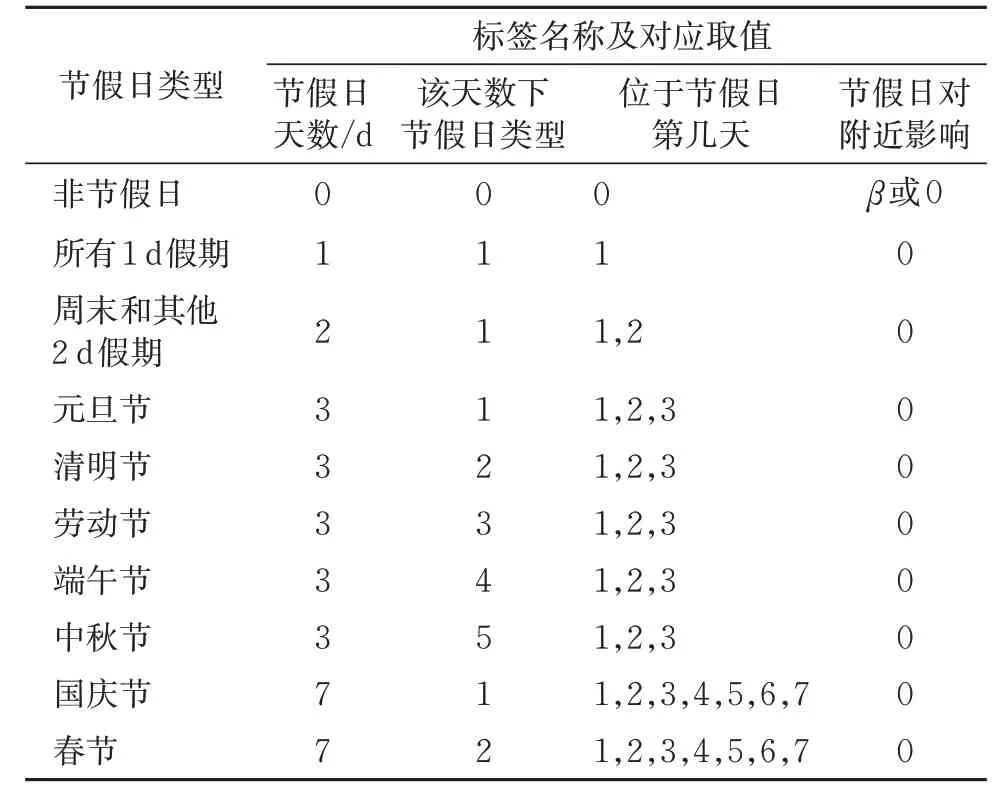
表3 节假日标签取值范围
2 预测模型及方法
2.1 预测模型
高铁的日客流量是随着日期的变化而动态变化的[13]。一方面,最近若干天的日客流量显然会对接下来这1天或几天的日客流量产生影响,即日客流量具有一定的自回归现象;另一方面,预测期各天的日期和节假日属性也会对日客流量产生影响。
为同时体现上述2 方面的影响,设计双层平行小波神经网络(Double Layer Parallel Wavelet Neu⁃ral Network, DLP-WNN)高速铁路日客流量中期预测模型,模型包括子网络1 和子网络2 这2 个上下平行的神经网络,如图7 所示。图中:ζBias为1 个较小的常数项;f为神经元传递函数,本文采用的是Morlet 母小波基函数[14],其函数表达式见式(2);每1 个椭圆表示1 个神经元,n1,1,n2,1和n3,1分别为子网络1 的第1~3 层神经元个数,n1,2,n2,2和n3,2分别为子网络2 的第1~3 层神经元个数;各层神经元之间的虚线连接箭头表示它们之间的加权求和计算,每1 条虚线对应1 个权值参数,例如w1,2,1表示第1层各神经元至第2层各神经元在子网络1的权值参数矩阵,其余类同。
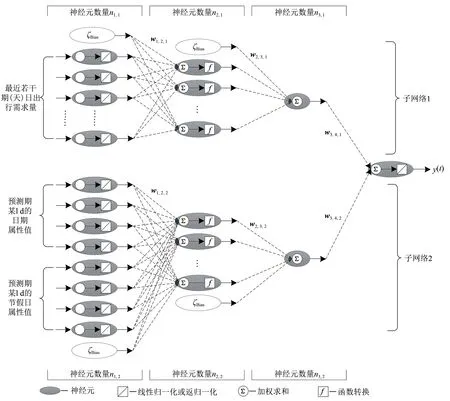
图7 日客流量中期预测DLP-WNN模型
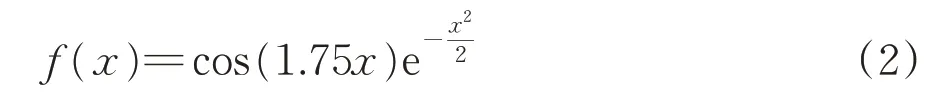
式中:x为神经元输入数据。
子网络1 体现的是日客流量的自回归特征,即预测期当天的客流量受其前面若干天的日客流量影响,这里借鉴TSAI 等[1]的处理手段,采用移动固定数据窗的方式输入数据,即随着日期的递进,在子网络1 的第1 层中每次固定输入最近第n1,1-1天的日客流量数据;子网络2 则是体现预测日当天日期属性和节假日属性对其日客流量的影响,其第1 层输入层由该天对应的4 个日期标签值和4 个节假日标签值以及1 个ζBias项组成。将2 个子网络的输出值加权求和,则得到整个网络的输出,即1 d客流量的预测值;通过该模型进行连续120 d 的预测,就能够获得中期日客流量预测结果。
根据图7 中DLP-WNN 模型设计中期日客流量的预测过程,如图8 所示。子网络1 的输入值是预测日前面若干天的客流量,在最开始第1天预测时,其输入值是历史日客流量数据;随着预测天数推进,后续输入值就逐渐更新为前面若干天已预测结果,因此可以将子网络1 的输入视为预测型数据。以预测型数据再继续进行预测,会形成误差累积,从而影响预测精度,这也是短期预测方法应用于中期预测时出现的普遍问题。为解决这种误差累积,本文设计了2 个子网络,由子网络2 对子网络1 的输出结果进行修正:由于子网络2 的输入值分别是各个预测日的时间属性标签值和节假日属性标签值,这些属性标签值是确定的且可以提前标定的,属于确定型输入数据;确定型数据经过对历史数据客流数据的学习,综合体现了常规日客流量的周期性规律(时间属性)和节假日的突变特点(节假日属性),所以得到的预测结果可以对子网络1所产生误差进行修正;对2 个子网络每天输出值加权求和即可得到各天的预测结果,该结果既可以延续日客流量的趋势又能够体现不同日期之间特别是节假日的客流量差异,有助于保证预测精度。
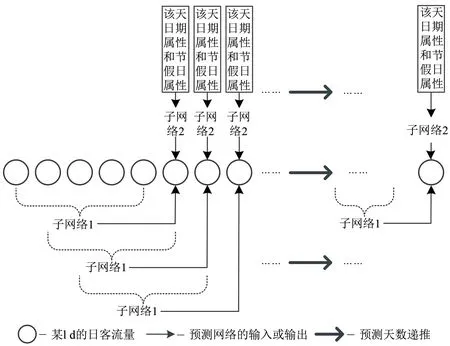
图8 基于DLP-WNN模型的日客流量中期预测流程
2.2 模型原理及流程
1)网络顺向预测
DLP-WNN 模型中2个子网络都是小波神经网络结构,采用小波基函数作为中间层的传递函数,并借鉴BP 神经网络设计思路,在进行信号前向传播的同时进行误差反向传播。为简化表达,现以子网络1为例说明预测原理及作业流程。
记子网络1 中,第1 层输入层各个神经元输入数据线性归一化后分别为x1,1(i),i=1,2,…,n1,1,将第1 层各神经元数据加权计算,得到第2 层各神经元h2,1(j),j=1,2,…,n2,1,其计算式为

式中:h2,1(j)为子网络1 第2 层的第j个节点值;w1,2,1(i,j)为子网络1 中第1 层第i个神经元与第2层第j个神经元的连接权值;bj为小波基函数的平移因子;aj为小波基函数的伸缩因子。
子网络1 第2 层各神经元h2,1(j)经过小波基函数传递之后得到输出值g2,1(j),其计算式为

然后,子网络1 第3 层各神经元h3,1(k),k=1,2,…,n3,1的计算式为
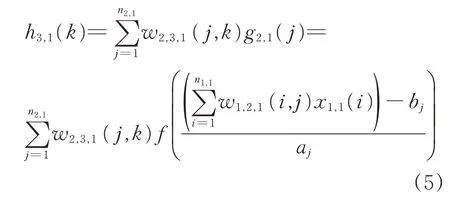
式中:h3,1(k)为子网络1 第3 层第k个节点值;w2,3,1(j,k)为子网络1 中第2 层第j个神经元与第3层第k个神经元的连接权值。
于是,对于整个DLP-WNN 网络,将子网络1和子网络2 各天的预测值加权求和,即可得到各天的预测输出。对于任意第t天的日客流量预测输出y(t),其计算式为
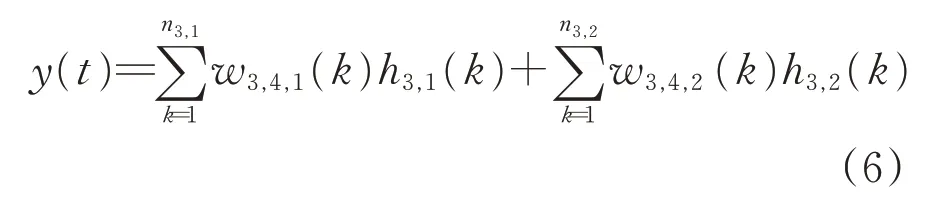
2)网络权值修正
除了对整个网络进行顺向预测之外,还需要利用误差逆向传播过程,对网络进行权值修正。在修正过程中,采用梯度下降法修正网络权值,使网络输出结果不断逼近期望输出。
记第t天的实际日客流量为ŷ(t),则预测精度误差E的计算式为
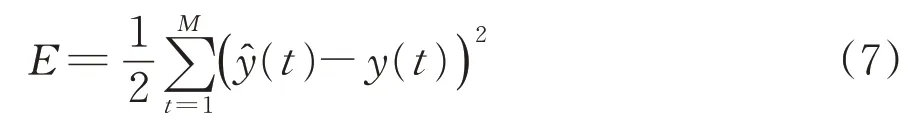
式中:M为训练数据总天数,d。
于是,网络权值的修正计算式为
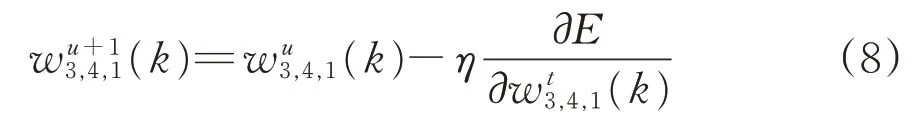
式中:u为训练次数,次。
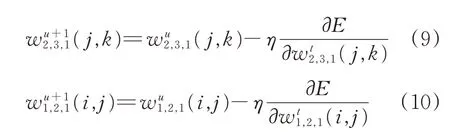
式中:η为学习速率。
计算误差E对于各层权重的偏导为
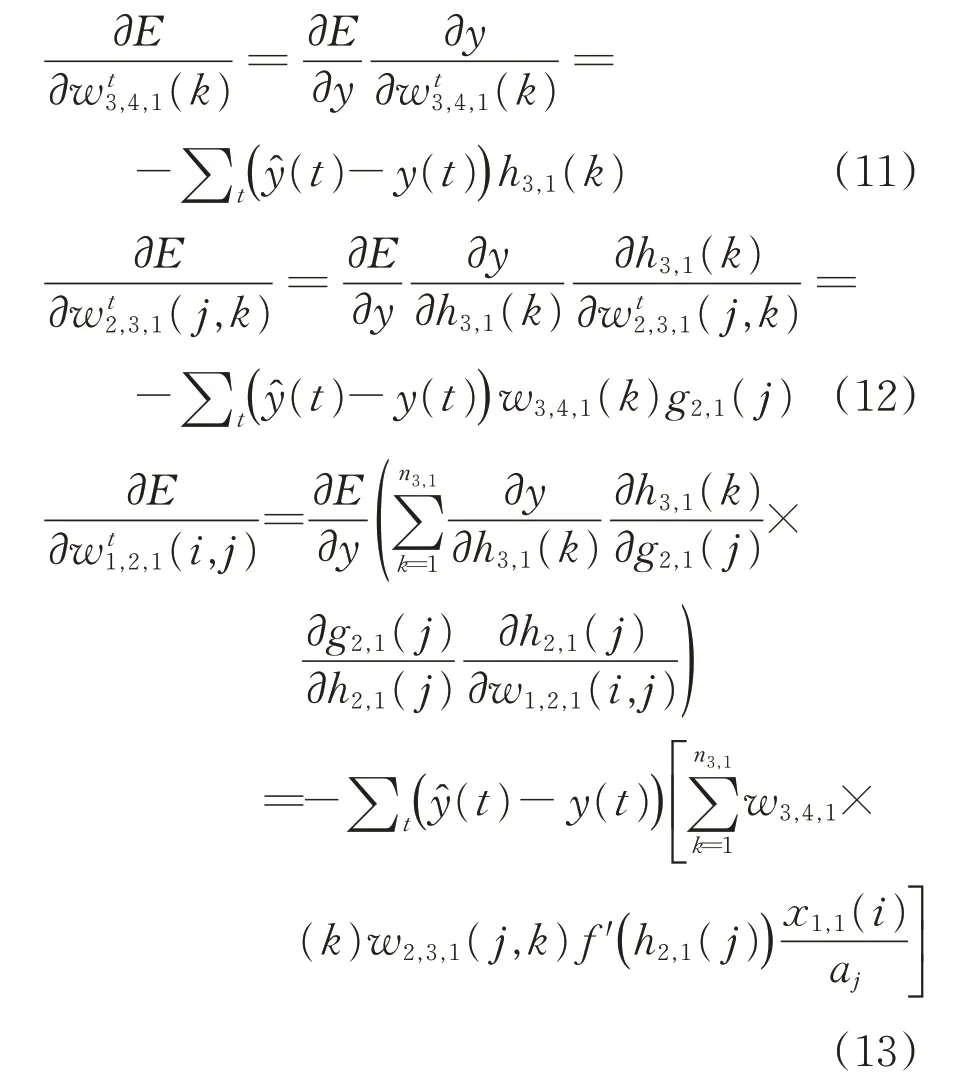
其中,
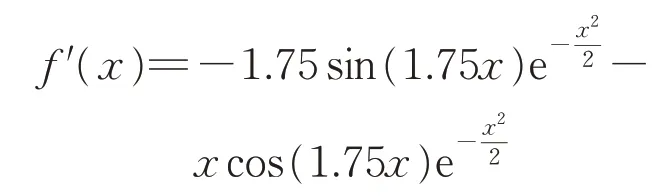
式中:f'(h2,1(j))为Morlet母小波基函数的导数。
当网络训练完毕后,可以使用其进行连续N=120 d 的预测,然后采用平均绝对百分比误差MMAPE和均方根误差RRMSE来评价Nd预测误差,其计算式分别为
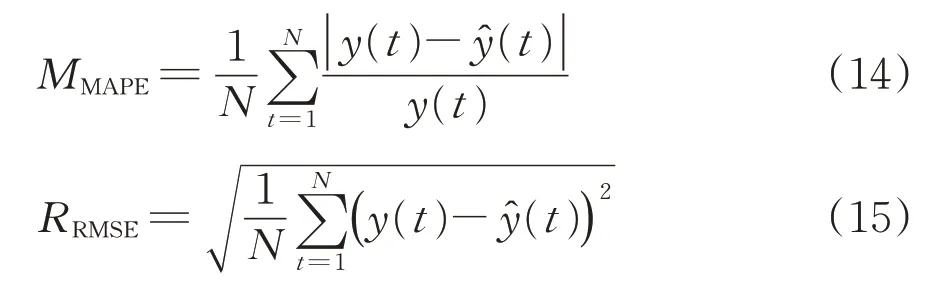
3 算例分析
3.1 数据输入
京沪高铁全长1 318 km,沿线设车站24 个,从中选取短距离、中等距离、中长距离和长距离这4 种不同距离下的典型O-D 对分别开展预测分析,具体的选取情况见表4。

表4 不同距离下的典型O-D对选取情况
针对上述4 种距离类型的O-D 对,以2014-01-01—2016-12-31 之间的高铁售票数据进行分析。以2014-01-01—2016-09-02 的日客流量数据作为训练集,采用DLP-WNN 模型进行训练,以2016-09-03—2016-12-31 这120 d 的日客流量作为测试集,通过分析对比预测结果与实际值的误差,评估本文提出预测方法的合理性和有效性。
3.2 预测效果

4种不同距离下典型O-D对的中期日客流量预测结果分别如图9所示。从图中可以看出,除了极少数点之外,在120 d 的连续预测中,总体上4 种O-D 对的日客流量预测值与实际值误差都比较小。整理预测结果的平均绝对百分比误差MMAPE和均方根误差RRMSE见表5。从表中的误差统计数据可以看出,4 种O-D 对的120 d 中期日客流量预测的MMAPE均在7%~12% 之间。图4 和表5可说明DLP-WNN 模型对于中期120 d 的日客流量预测具有较好的精度和效果。

图9 4种不同距离下的典型O-D对中期预测结果
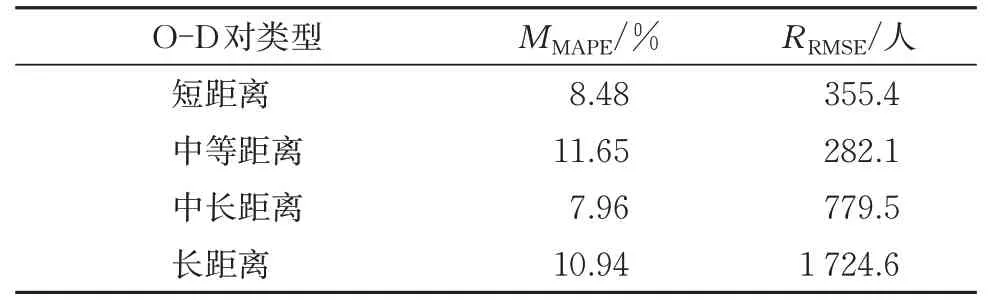
表5 不同类型O-D对的中期预测误差分析
为进一步检验预测效果,将DLP-WNN 预测模型与其它方法进行预测对比。分别采用BP 神经网络、ELM 极限学习机、ELMAN 神经网络、GRNN 广义回归神经网络和VMD-GA-BP(变分模态分解-遗传-BP 神经网络)[15]等预测方法,对上述4 种不同距离下典型O-D 对进行120 d 的中期日客流量预测,效果对比如图10所示。
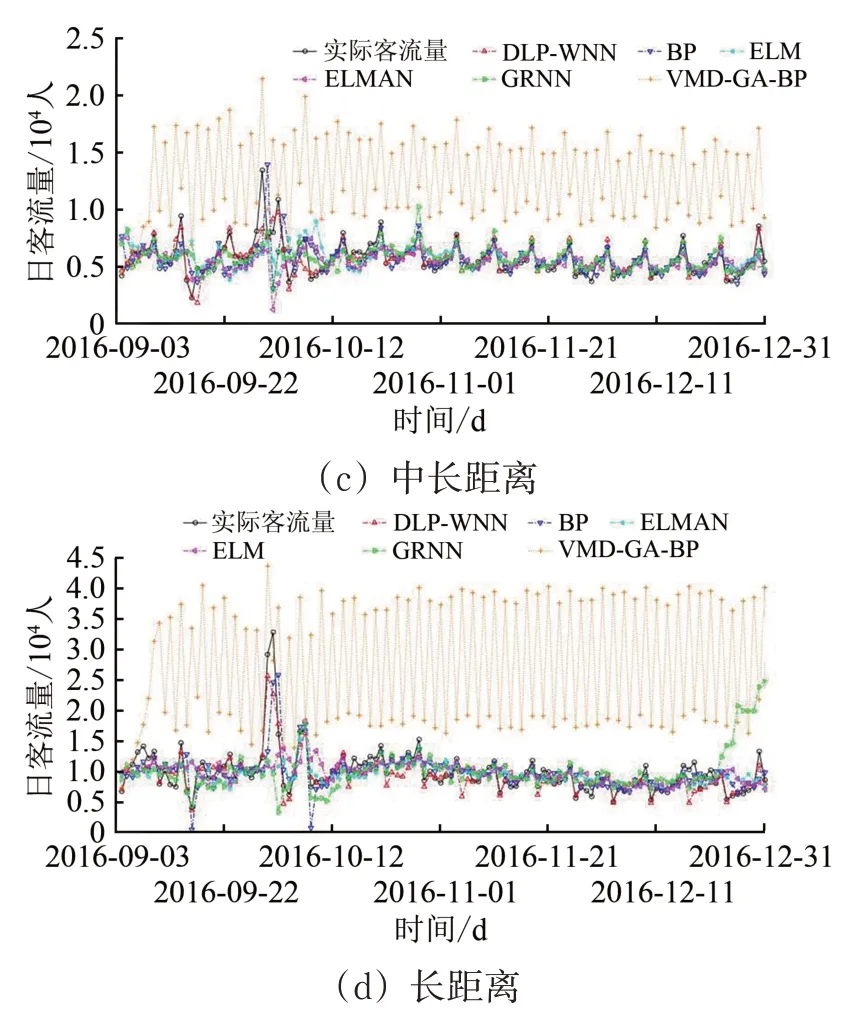
图10 不同预测方法下4种O-D对的120 d日客流量中期预测效果对比
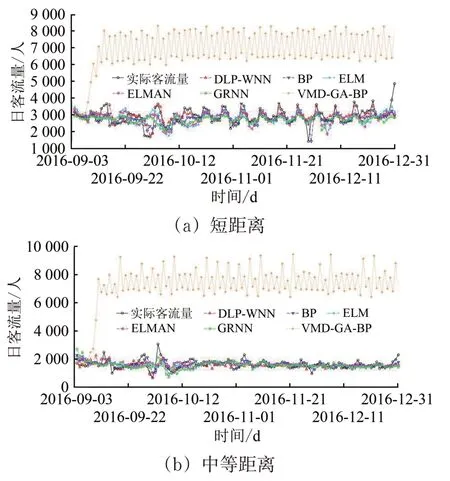
从图10 可以看出:DLP-WNN 预测方法对4种不同距离下典型O-D 对的中期预测效果都是最好的;对于VMD-GA-BP 方法,其在预测期最开始的几天效果不错,但随着预测天数的增加,该方法的预测偏差是最大的,这说明该方法只适合于短期预测,不适合用于中期预测。不同预测方法下4种O-D 对的120 d日客流量中期预测结果的平均绝对百分比误差MMAPE和均方根误差RRMSE分别见表6和表7。从表6 和表7 同样可以看出,DLP-WNN预测方法的误差最小。
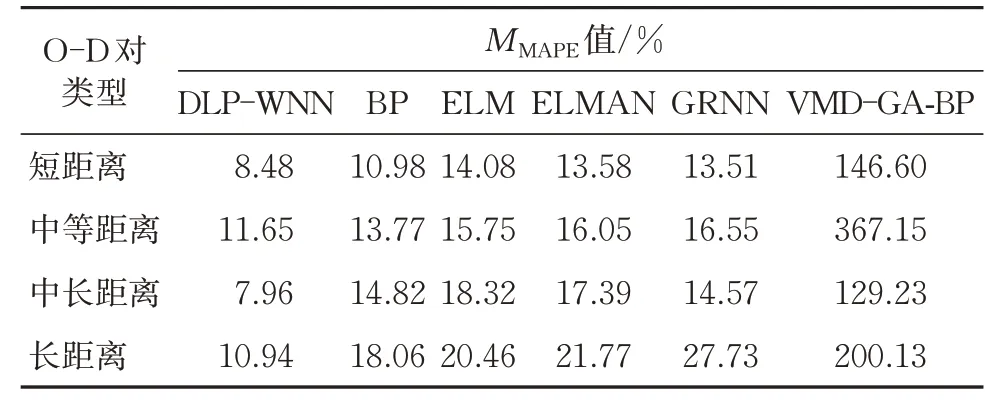
表6 不同预测方法下120 d日客流量中期预测的MMAPE值对比
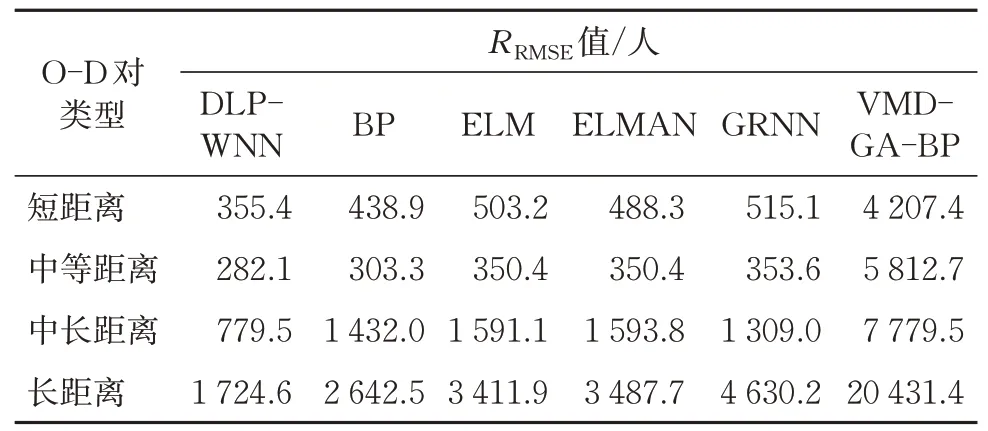
表7 不同预测方法下120 d日客流量中期预测的RRMSE值对比
上述分析均表明,DLP-WNN 模型适用于高速铁路旅客日客流量中期预测。
4 结 语
本文基于2014—2016年北京至上海所有日客流量数据,首先分析了非节假日和节假日的高铁日客流量特征,分别体现了日客流量变化的动态周期特征和节假日属性影响特征,基于该特征对应设计了日期和节假日2 类标签;结合高铁日客流量的自回归特征,构建了高铁日客流量中期预测DLPWNN 双层平行小波神经网络模型,通过对2 个平行的小波神经网络输出值的加权求和来获得具体的日客流量预测输出,其中,子网络1体现的是预测日之前若干天的日客流量对于预测日当天客流量的影响,子网络2 体现的是预测日当天的时间属性和节假日属性对当天客流量的影响;分别以京沪高铁中的短距离、中等距离、中长距离和长距离这4种距离下的典型O-D 对为算例,应用DLP-WNN 模型进行为期120 d 的中期日客流量预测,并与其它5 种预测方法进行预测误差的分析对比,体现本文所提出的中期预测方法的合理性和有效性。
需要注意的是,本文所构建的预测模型是基于历史客流数据执行特征学习和预测,其隐含前提条件是过去情况会继续延续到以后,也就是说在高铁运输市场不发生剧烈变动的前提情况下,本文所提出的中期预测方法效果是较好的。但是,若出现疫情暴发或客流管控等极端情况时,当历史数据暂时还没有包含相应的类型特征时,预测效果将受到影响。当然,若能够进一步分析疫情期间客流特征,则可尝试借鉴本文思路设计适当标签以构建预测模型,这里暂不做详细讨论,可将其作为下一步的研究内容。

