初中数学最短路径问题的教学探究
郭绪娥

[摘 要]最短路径问题是中考数学的高频考点,问题虽不难,但很多学生却答不出来.探讨最短路径问题的解法,能提高学生的解题能力.
[关键词]最短路径;问题;初中数学
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)32-0013-02
青島市数学中考中每年都有一个求最短路径的问题,这类问题虽然不难,但往往有一大批学生答不出来.针对这类问题,笔者进行了研究,经研究发现,如果教师在教学方面做足功夫,学生的数学素养就会得到提高,就可以让学生解题时得心应手.
一、数学几何模型
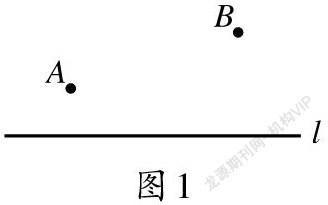
北师大版初中数学七年级下册第123页有这样一道题:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
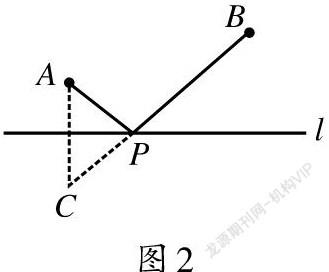
我们都知道这个问题的解决方法是作A关于直线l的对称点C,连接BC交街道l于P,则P为所求,如图2所示.即要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在P处,才能使从A、B到它的距离之和最短.
那么为什么要作一个关于l的对称点?如何利用学生已有的知识储备进行迁移,才能使学生易于接受?笔者先让学生完成下面的题目.
如图3,在河的两岸有两个村庄A、B,现在要在公路l上建一个汽车站C使汽车站到A、B两村庄的距离之和最小,则汽车站C的位置应该如何确定?
这个问题学生都知道应连接A、B两点,AB与直线l的交点就是点C的位置.
通过这个问题的解决,再把这个题目和轴对称进行联系,学生就会觉得非常容易接受.
二、几何模型的应用
1.如图4,菱形ABCD的两条对角线长分别为6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则[PM+PN]的最小值是多少?
这个问题中对应上述题目的“公路”就是AC,M、N为那两个点,通过找对称点和利用菱形的性质就会发现[PM+PN]的最小值等于菱形的边长.因此,解决这个问题的同时把菱形的性质也进行了复习和巩固.
2.如图5,正方形ABCD的边长为4,E是BC的中点,P为对角线BD上的动点,要使[PE+PC]的值最小,试确定点P的位置,并求出最小值.
要解决这个问题,就要引导学生找出图形中的“公路”和两个点.不难发现,这个问题中的“公路”就是BD,两个点就是E、C.图形中已经给出了C点关于DB的对称点A,连接AE,AE与BD的交点就是要求的点P,P点找出来后,就会发现[PE+PC]的最小值是线段AE的长.
通过这两个问题的解决,模型又得到了提升,两条线段和的最小值最后转化为求一条线段的长度.
三、几何模型生成的问题
1.如图6,圆柱形玻璃杯高为12 cm、底面周长为18 cm,在杯内离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_______________cm.
这是青岛市2012年的中考题.通过玻璃杯的内外壁的展开图(如图7)不难发现玻璃杯的上边沿所在的直线就是模型中的“公路”,而A、B就是模型中的两个点,最短距离就转化为求线段AB′的长度.这样又把勾股定理及其逆定理进行了复习和巩固.
四、几何模型与代数问题的结合
1.如图8,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,[OA=3],[OB=4],D为边OB的中点.
(1)点D的坐标为_____________________;
(2)若E为边OA上的一个动点,当[△CDE]的周长最小时,求点E的坐标.
这个问题中的第(1)问非常容易解决.第(2)问如果求[△CDE]的周长最小,也比较容易解决.但要求点E的坐标,这就和一次函数联系起来了.到此几何与代数已经比较紧密地结合起来,我们教师不能简单地照本宣科.如何提高学生的数学能力,培养学生的数学素养?这就需要我们教师潜心研究教材.为了进一步培养学生的数学素养,我们再来看下面的题目.
2.如图9,C为线段BD上一动点,分别过点B、D作[AB⊥BD],[ED⊥BD],连接AC、EC.已知[AB=2],[DE=1],[BD=8],设[CD=x].
(1)用含x的代数式表示[AC+CE]的长;
(2)点C满足什么条件时,[AC+CE]的值最小?
(3)根据(2)中的规律和结论,求出代数式[x2+4+12-x2+9]的最小值.
这个问题进一步把几何问题和代数问题紧密结合起来,特别是第(3)问,看似是求一个算术平方根的和的最小值.如果教学中没有前面这些铺垫,单独拿出这个问题,学生基本解决不了.有了前面的铺垫,就容易想到构造几何图形,进一步应用勾股定理求出代数式的最小值.
五、拓展提高
1.如图10,已知[∠AOB=45°],P是[∠AOB]内部一点,且[OP=2 cm],点E、F分别在射线OA、OB上,找出E、F两点,使[△PEF]周长的最小,并求出最小值.
这个问题学生往往容易认为过P作OA、OB的垂线,垂足就是所求的点.实际上这是错误的.通过图11,我们就会发现[△PEF]的周长等于线段MN的长,因此,如何求线段MN的长是解决本题的关键.题目中的已知条件[∠AOB=45°]还没有用,如何应用这个条件?这个条件对我们解决问题有什么作用?带着这些问题去思考.如图12,连接[OM]、[ON]就会发现[∠MON=2×45°=90°],这样利用轴对称的性质和勾股定理就可以解决问题.
以上是笔者在教学中对最短路径问题的研究,有不当之处敬请批评指正.
(责任编辑 黄桂坚)

