面向无人驾驶矿车的露天矿山道路坡度实时检测方法

孟德将，田 滨，蔡 峰，高义军，陈 龙

1. 北京慧拓无限科技有限公司，北京 100190； 2. 中国科学院自动化研究所复杂系统管理与控制国家重点实验室，北京 100190； 3. 中国科学院大学人工智能学院，北京 100190； 4. 中国中煤能源集团有限公司，北京 100120； 5. 安徽马钢矿业资源集团南山矿业有限公司，马鞍山 243031； 6. 中山大学数据科学与计算机学院，广州 510006

智慧矿山已经成为矿山发展的方向。露天矿山道路坡度变化范围大，无人驾驶矿车容易发生因下坡急减速导致的物料外撒或因上坡导致的溜车等危险。无人驾驶矿车需要精确检测车辆前方一定范围内的道路坡度，辅助速度规划合理规划速度，才能避免危险的发生。无人驾驶矿车依据道路坡度合理规划速度后，还可以提升运输的效率。

目前可以用于无人驾驶矿车实时检测露天矿山道路坡度的方法主要分为4类。

(1) 基于INS或GNSS，直接从车载高精度的INS读取俯仰角、基于GNSS单天线计算水平与竖直方向的速度比或基于GNSS双天线提取信号的低频部分等作为道路的坡度[1-5]。这一类方法在道路坡度小且平整的结构化场景中精确度较高，但是在检测露天矿山道路坡度时有两个挑战：①矿山道路坡度大且不平整，矿车在行驶过程中的俯仰和弹跳运动会降低检测精确度；②无法实时检测车辆前方的道路坡度。

(2) 基于SLAM算法，首先提取周围环境的线、面等特征；然后利用帧间匹配算法或地图匹配算法等构建精确的三维环境地图；最后可以检测道路坡度[6-12]。这一类方法在几何特征明显的结构化场景中的精确度比较高，但是在检测露天矿山道路坡度时有一个挑战：露天矿山几乎没有树木和建筑，几何特征缺失，在一些特征缺失严重的路段容易匹配错误，导致道路坡度检测精确度较低。同时，这一类方法测出的也是车辆的俯仰角，而不是道路的坡度。

(3) 基于卡尔曼滤波器或龙伯格(Luenberger)观测器等，通过分析车辆的受外力情况建立车辆模型，进而利用动力学的方法估计道路的坡度[13-19]。这一类方法无须借助昂贵的激光雷达或INS，但是该方法检测道路坡度会受到车辆动力学性能和道路条件的影响，露天矿山道路不平整，同时获取的矿车动力学参数也存在误差，所以很难获得精确的道路坡度。

(4) 基于激光雷达的方法。激光雷达可以实时精确地获得周围环境的三维位置信息，基于激光雷达的这个特点，已经提出了很多地形检测的方法。研究比较多的地形包括路沿(路面)、凹坑等。路沿(路面)的研究方法主要分为两类：一类基于传统方法，首先使用高度差、ILP(integral laser points)等特征提取路沿候选点，然后使用霍夫变换、B样条等方法对路沿候选点进行曲线拟合，提取最终的道路边界[20-21]；另外一类基于机器学习或深度学习的方法，使用CNN(convolutional neural network)或DCNN(deep convolutional neural network)等对路面进行分割，从而提取路面[22-23]。凹坑主要采用传统方法，一种方法是首先通过投影获得点云深度图，然后在点云深度图的基础上采用激光雷达直方图及点云分割的方法检测凹坑[24]；另一种方法是直接利用原始的激光点云之间的几何关系检测凹坑[25]。虽然基于激光雷达检测地形的方法比较多，但是公开的基于激光雷达检测道路坡度的方法还比较少。目前基于激光雷达检测道路坡度的方法首先通过提取打在斜坡上的点云，然后使用PROSAC(progressive sample consensus)、RANSAC(random sample consensus)等平面拟合的方法得到斜坡坡面方程，进而获得道路坡度[26-27]。因为这一类方法没有融合INS姿态角信息，无法检测道路相对于水平面的坡度，所以，在坡度小且平整的结构化场景中的道路坡度检测精确度还比较高，而在露天矿山场景下，则对道路坡度的检测精确度就比较差。

针对目前无人驾驶矿车实时检测露天矿山道路坡度研究中存在的问题，利用激光雷达可以实时精确地获得环境三维位置信息及INS可以实时精确获得INS坐标系相对于水平面姿态角的特点，本文提出了栅格卡尔曼道路坡度实时检测(grid Kalman road slope real-time detection，GKSRD)方法。该方法以三维激光雷达点云和INS俯仰角信息作为输入，并采用二维栅格地图、感兴趣矩形区域迭代优化算法和卡尔曼滤波器。相比于基于INS或GNSS的方法，该方法减小了无人驾驶矿车行驶过程中由于道路坡度大且不平整对道路坡度实时检测带来的误差。相比于基于SLAM的方法，因为该方法不依赖周围环境的几何特征，所以其不会受到露天矿山几何特征缺失的影响。同时，相比于基于激光雷达的方法，该方法融合了INS俯仰角信息，可以更加精确地检测露天矿山的道路坡度。经过试验验证，该方法在露天矿山复杂的道路条件下可以实时、精确地检测车辆前方道路某一区域的坡度。

1 栅格卡尔曼道路坡度实时检测(GKSRD)方法

露天矿山道路坡度变化范围大且不平整，无人驾驶矿车会有比较大的俯仰和弹跳运动。同时，露天矿山几何特征缺失。为了精确地提取露天矿山道路的坡度，本文提出了栅格卡尔曼道路坡度实时检测方法。激光雷达可以提供精确的环境三维信息。INS可以提供INS坐标系相对于水平面的精确姿态信息。本文方法融合激光雷达和INS作为输入，可以在很大程度上降低无人驾驶矿车在运动过程中的俯仰和弹跳运动对道路坡度提取的影响。传感器融合必须保证不同传感器有统一的坐标表示，本文采用文献[28]的方法对INS和激光雷达进行联合标定，获得INS坐标系与激光雷达坐标系之间的相对位姿关系。该方法适用于机械式旋转雷达和固态雷达，如果是前者，输出的点云会发生运动畸变，本文基于匀速运动模型[29]对点云进行运动畸变矫正。

本文方法输出的道路坡度是实时检测的，即只用到了当前帧和历史帧的数据，没有用到未来帧的数据。根据露天矿山道路的实际情况，方法忽略无人驾驶矿车的侧倾运动，只融合INS俯仰角，从而获得点云在INS水平坐标系下的三维坐标，INS水平坐标系原点与INS坐标系原点重合。无人驾驶矿车主要关心车辆行驶方向的道路坡度，不关心另外两个维度的道路坡度，因此，本文方法基于二维栅格地图计算道路坡度，将INS水平坐标系下的点云投影到二维栅格地图，栅格的值为点云的高度，从而获得二维高度栅格地图[30]。相比于实际的道路坡度变化情况，由于本文方法采用的二维栅格的分辨率比较高，所以基于二维栅格地图计算车辆行驶方向的道路坡度不仅对检测的精确度影响不大，还能在很大程度上减少时间成本。在二维高度栅格地图中定义一个用于计算道路坡度的感兴趣矩形区域，矩形区域相对于INS水平坐标系原点的位置以及矩形区域的大小是固定的。将感兴趣矩形区域划分为远近两部分，使用感兴趣矩形区域迭代优化算法分别计算每一部分的高度值，进而计算整个感兴趣矩形区域的坡度初始值。基于坡度初始值，融合卡尔曼滤波器，即可提取精确的实时道路坡度。

1.1 二维高度栅格地图构建

本文方法基于二维高度栅格地图检测道路坡度，首先需要构建二维高度栅格地图。如图1所示，x0y0z0为激光雷达坐标系，xyz为车体坐标系，车体坐标系的xy平面与车底板平行，x1y1z1为INS坐标系，x2y2z2为INS水平坐标系，INS水平坐标系的x2y2平面与水平面平行。

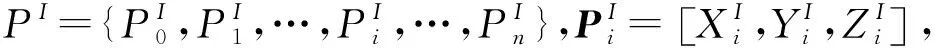
(1)

(2)

式中，λ1为INS相对于车底板的角度安装误差；λ2为由于车辆俯仰运动产生的车底板与路面的夹角；λ3为车辆所在道路的坡度；λ1+λ2+λ3为INS的俯仰角。

根据式(3)将PL投影到二维栅格地图，可以获得二维高度栅格地图

(3)

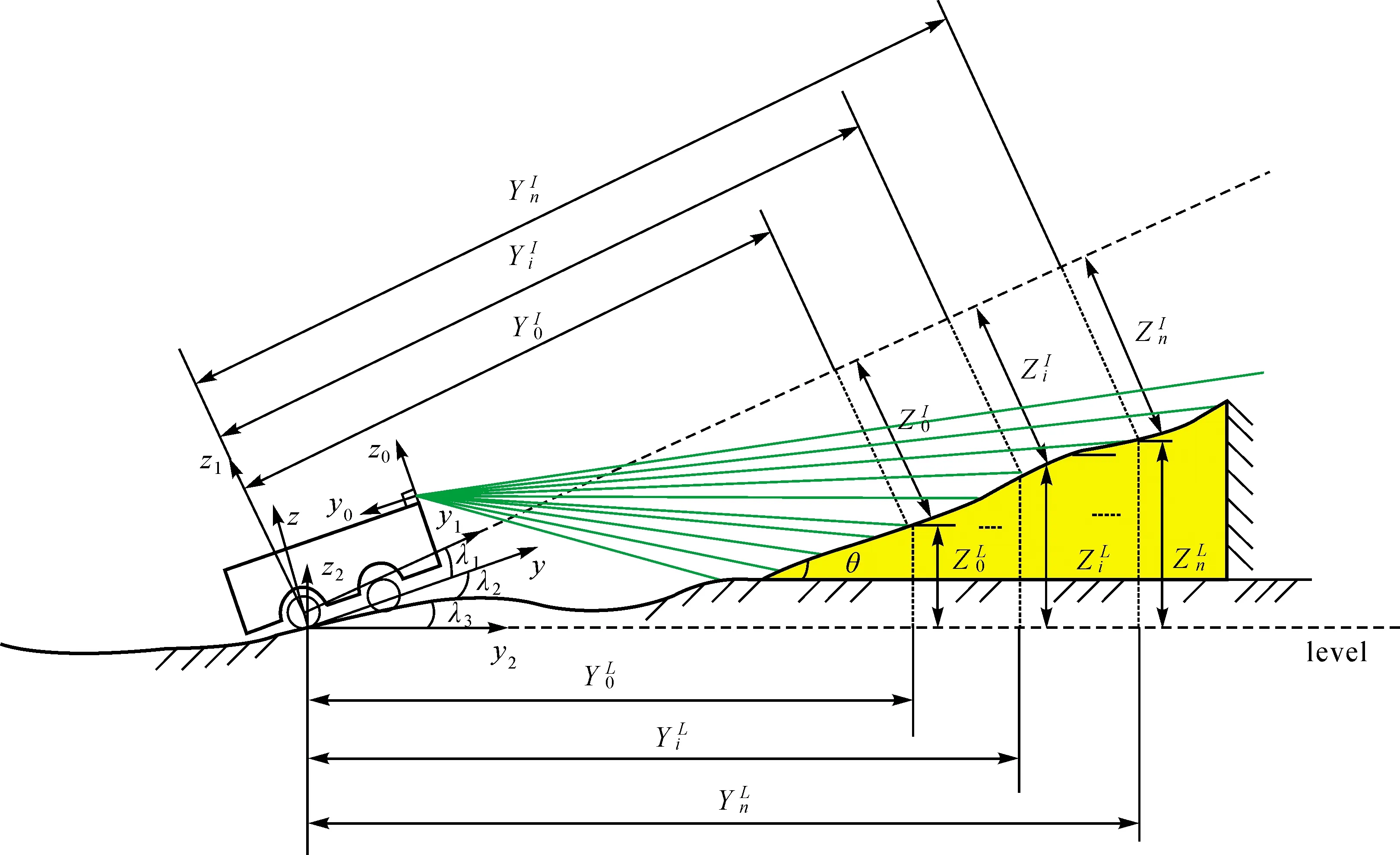
图1 道路坡度实时检测示意Fig.1 A diagram of road slope real-time detection

式中，Zindex为索引index的栅格的高度；其中index与i满足

i∈[0,n]

(4)

1.2 感兴趣矩形区域迭代优化算法

建立了二维高度栅格地图后，即可进行道路坡度计算。首先需要确定栅格地图中的感兴趣矩形区域。为了使感兴趣矩形区域中有尽量多的值不为0的栅格，感兴趣矩形区域选择在车辆前方道路点云比较密集的区域。根据实际情况，道路的宽度必然大于无人驾驶矿车的宽度，所以感兴趣矩形区域的宽一般略大于车宽。如图2所示，A与B分别为近处和远处的感兴趣矩形区域，组成了选定的感兴趣矩形区域。A与B的大小相同，位置相邻，且在二维栅格地图坐标系中的位置固定。

确定了二维栅格地图中的感兴趣矩形区域后，根据二维栅格地图矩形区域迭代优化算法可以分别计算A与B的几何中心位置(XA,YA)与(XB,YB)处的高度ZA和ZB。算法的输入包括二维高度栅格地图、矩形区域边界、初始迭代次数、迭代次数阈值、初始偏移量阈值、偏移量步长及标准差阈值。初始偏移量阈值、偏移量步长与标准差阈值配合筛选每次迭代时偏离均值较远的栅格。然后基于直角三角形模型，由式(5)可确定感兴趣区域A+B的几何中心位置的初始坡度

(5)

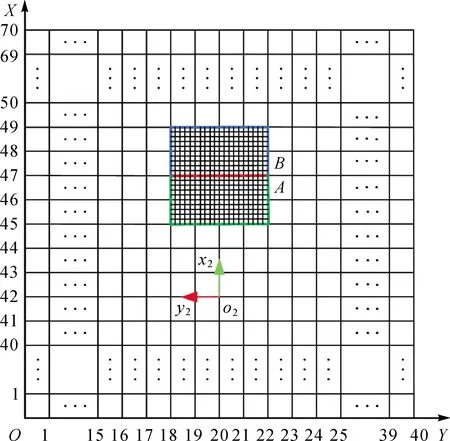
图2 二维栅格地图Fig.2 2D grid map

二维栅格地图矩形区域迭代优化算法如下。

输入：ogm二维高度栅格地图；minrow矩形区域下边界；maxrow矩形区域上边界；mincol矩形区域左边界；maxcol矩形区域右边界；count初始迭代次数；counthre迭代次数阈值；offsethre初始偏移量阈值；s偏移量步长；stdevthre标准差阈值

输出：mean矩形区域几何中心位置高度

1: function Interation(ogm, minrow, maxrow, mincol, maxcol, count, counthre, offsethre, stdevthre,s)

2: offsethre←offsethre-s

3: count++

4: totalvalue←0 矩形区域内部栅格值的总和

5: totalcell←0 矩形区域内部不为0的栅格的数量

6: array 保存矩形区域内部不为零的栅格的值的数组

7: width 栅格地图的宽，即列数

8: fori←minrow to maxrow step 1 do

9: forj←mincol to maxcol step 1 do

10: if ogm[i·width+j]>0 then

11: totalvalue←totalvalue+ogm[i·width+j]

12: array[totalcell]←ogm[i·width +j]

13: totalcell←totalcell+1

14: end if

15: end for

16: end for

17: mean←totalvalue / totalell

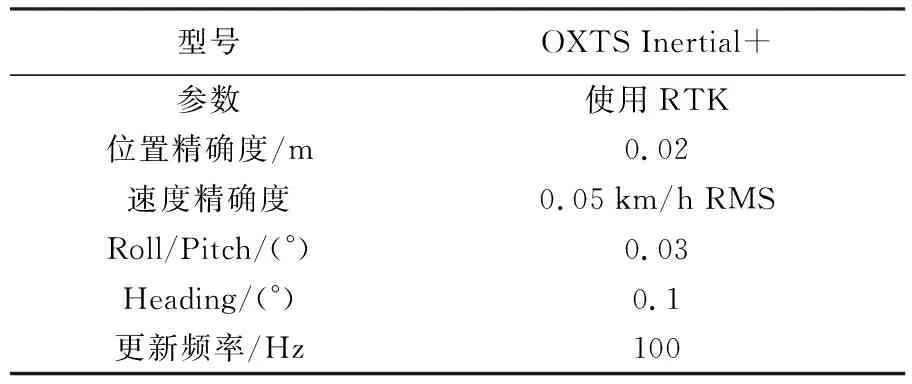
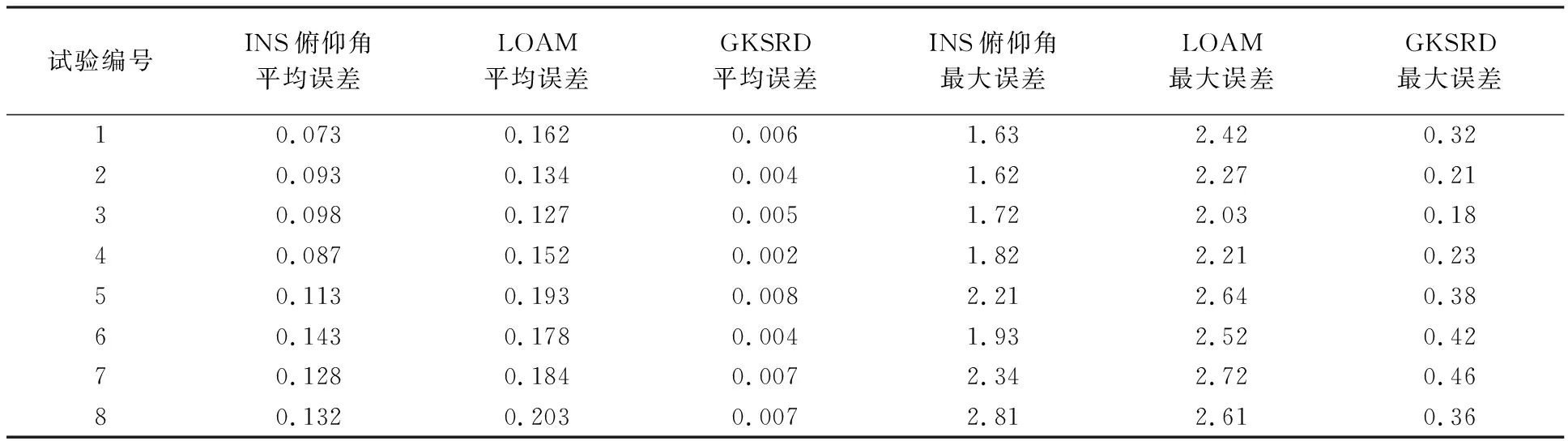
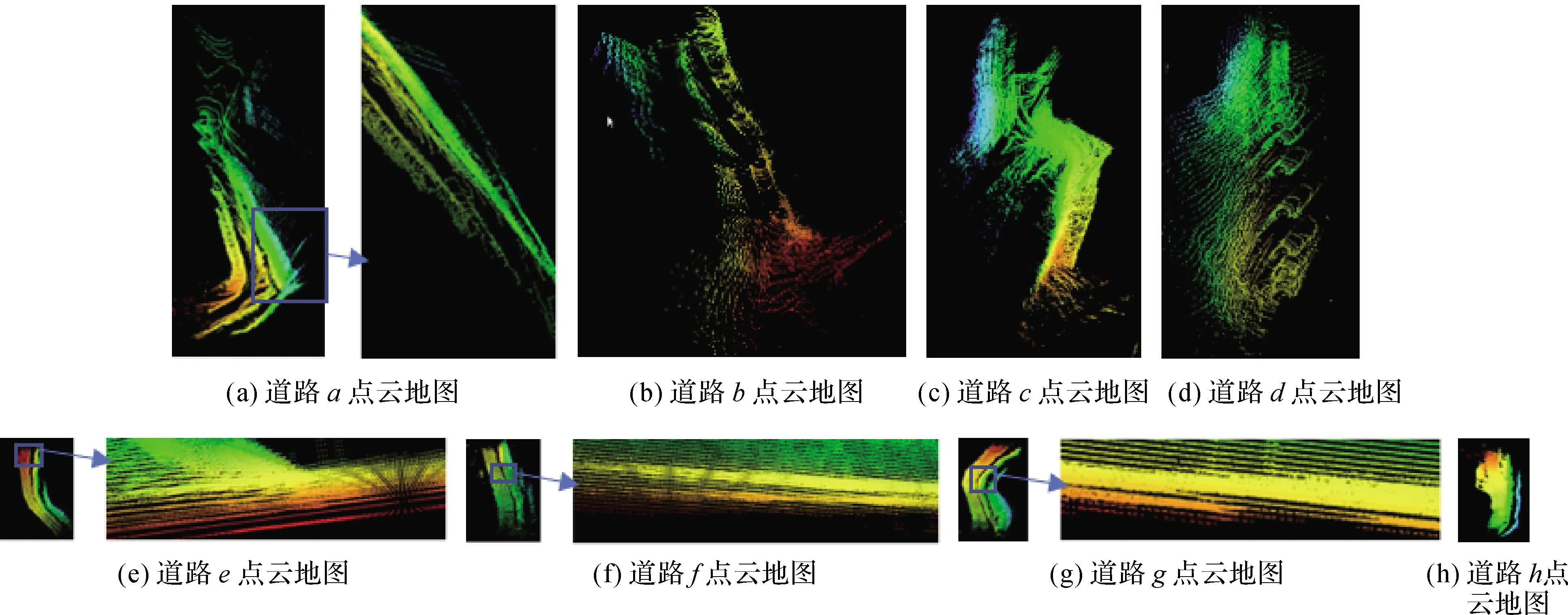
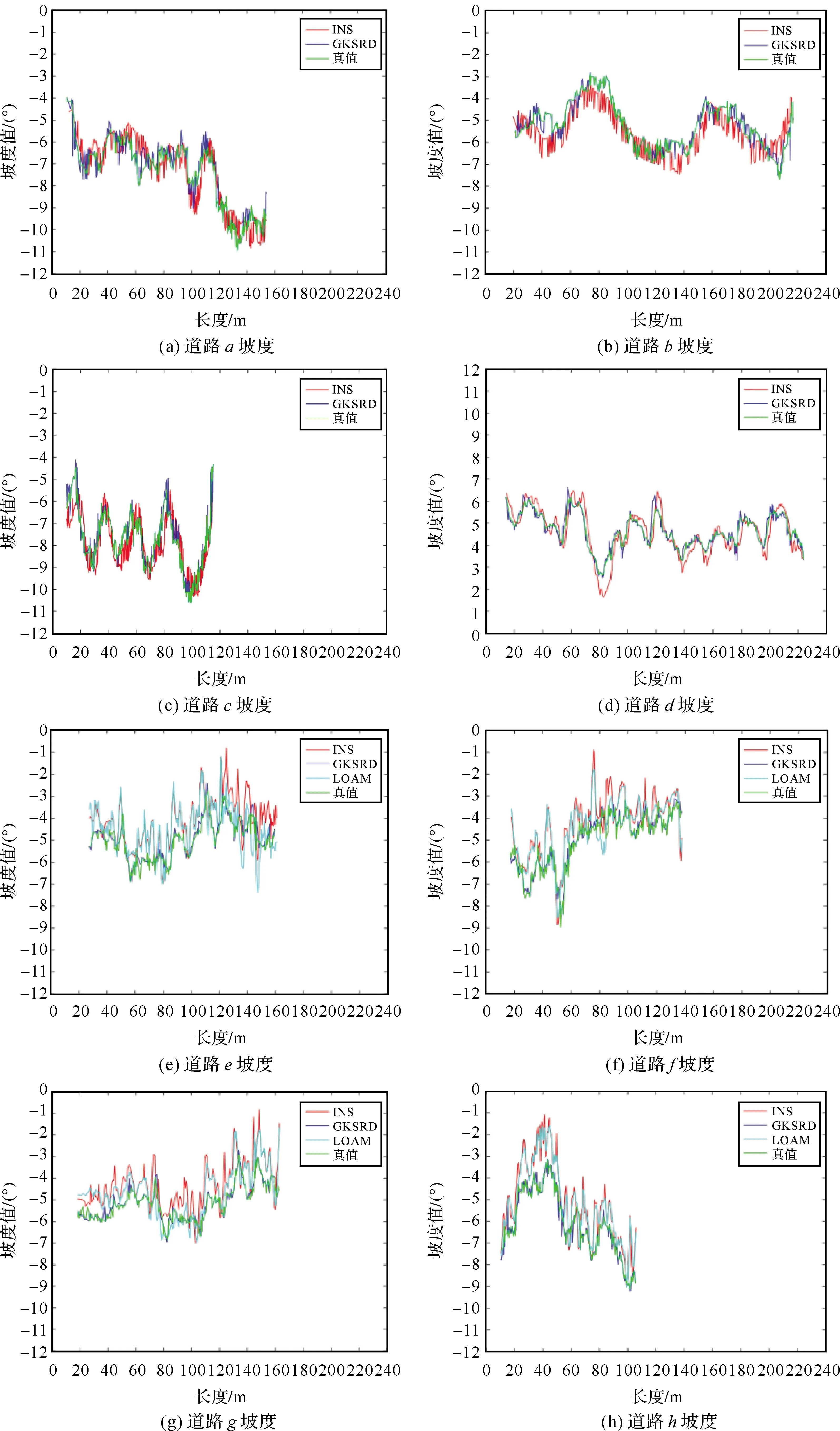
19: if stdev>stdevthre and count

offsethre>1 then

20: fori←minrow to maxrow step 1 do

21: forj←mincol to maxcol step 1 do

22: offset←|ogm[i·width+j] - mean|

23: if ogm[i·width+j]≠0 and offset>

offsethre then

24: ogm[i·width+j]←0

25: end if

26: end for

27: end for

28: return

29: function Interation(ogm, minrow, maxrow,

mincol, maxcol, count, counthre, offsethre, stdevthre,s)

30: else

31: return mean

32: end if

33: end function

1.3 基于卡尔曼滤波器的结果优化

GKSRD方法的前两步已经求出了当前帧感兴趣矩形区域几何中心位置的道路初始坡度。根据实际情况，基于相邻帧道路坡度均匀变化模型，融合卡尔曼滤波器，GKSRD方法可以进一步优化当前帧感兴趣矩形区域几何中心位置的道路坡度，优化的结果即为GKSRD方法最终的道路坡度实时提取结果。相邻帧道路坡度均匀变化模型是指相邻帧的感兴趣矩形区域几何中心位置的道路坡度均匀变化。

卡尔曼滤波器由两个步骤描述：估计和测量更新。

第1步：估计。当前帧的状态估计向量xk和误差协方差矩阵Pk根据式(6)和式(7)求得

xk=Fkxk-1

(6)

(7)

式中，xk-1为前一帧的感兴趣矩形区域几何中心位置的道路坡度测量更新结果，只包含道路坡度一个状态变量；Pk-1初始化为一行一列的单位矩阵；Fk为状态转移矩阵，基于相邻帧道路坡度均匀变化模型，令Fk=1；Qk为过程噪声协方差，本文方法中忽略过程噪声协方差，令Qk=0。

(8)

(9)

(10)

式中，Hk为尺度变换矩阵，令Hk=1；Rk为测量噪声协方差矩阵，本文方法中忽略测量噪声协方差，令Rk=0。

2 试验与分析

2.1 试验场景

为了验证本文方法的有效性，在两个不同的露天矿山进行试验。如图3所示，其中，图3(a)为内蒙古宝利露天煤矿，图3(b)为马鞍山和尚桥露天铁矿。图3(a)道路坡度大，路面相对平整；图3(b)道路坡度也很大，同时，路面有很多矿石，路面很不平整。

2.2 试验平台

本文采用的试验平台如图4所示，型号为临工集团CMT96非公路自卸车，车头左右两侧各安装一个三维激光雷达，型号为RS-LiDAR-16，部分性能参数信息见表1所示，紧贴车辆前轴中心正上方的车底板上安装一个惯性导航系统，型号为OXTS Inertial+，部分性能参数信息表2所示。

图3 试验场景Fig.3 Experimental scene

图4 试验平台Fig.4 Experimental platform

表1 RS-LIDAR-16性能参数

表2 OXTS Inertial+性能参数

由表1和表2可以看出激光雷达的测距精度可以达到2 cm，INS的Pitch精度可以达到0.03°。计算平台为工控机(industrial personal computer，IPC)，CPU(intel core i7-6820EQ)为四核八线程，主频2.8 GHz，运行内存为16 GB，系统环境为Ubuntu18.04系统，基于ROS(robot operating system)软件框架。

在试验中，为了使道路坡度真值尽量精确，INS由于安装误差，还需要进行安装误差矫正，误差矫正采用高精度的倾角仪，将车辆静止停放在一个平整的斜坡上，利用倾角仪测出斜坡的角度，同时读出INS的俯仰角，即可获得安装误差。经过安装误差矫正后，理论上，车载INS在静止状态下的俯仰角就是所在位置的道路坡度。

2.3 试验结果

本文在图3(a)和图3(b)的场景中各选择了3段道路作为试验对象，道路依次标记为a、b、c、d、e、f、g、h。在图3(a)道路车辆的速度为15 km/h，在图3(b)道路车辆的速度为10 km/h。栅格地图大小为40×70 m2，分辨率为0.2 m，坐标原点位于左下角，INS水平坐标系原点的坐标为(20,20)。如图5所示为部分道路坡度实时提取效果图，红色单元格的边长为10 m，白色矩形框为车辆位置，绿色为点云，粉色矩形框为感兴趣矩形区域，横向宽为5 m，纵向高为4 m，青色表示感兴趣矩形区域的坡度为正，红色表示感兴趣矩形区域的坡度为负。

2.4 试验结果分析与精度评价

为了尽量减小由于路面不平整和坡度大导致的车辆俯仰运动带来的误差，真值通过以下方式获得。记录每一组试验的起点，以该起点作为真值获得的起点，车辆每走大约1 m左右，停下来读取此时的INS俯仰角作为当前所在位置的道路坡度。这种获得真值的方式由于在车辆静止的时候读取INS俯仰角，所以在极大程度上减小了由于路面不平整和坡度大导致的车辆俯仰运动带来的误差。同时，为了验证GKSRD方法的有效性，本文进行的对比试验包括：以GKSRD方法的提取频率实时读取的INS俯仰角以及融合GNSS的LOAM算法，LOAM是目前主流的SLAM算法。

目前的一些基于激光雷达的方法只能提取相对于车体坐标系的道路坡度，所以对比试验结果分析中没有加入基于激光雷达的方法。同时，基于卡尔曼滤波器或龙伯格(Luenberger)观测器等的方法无法进行实时检测，所以也没有加入对比试验结果分析。

图6(a)、图6(b)、图6(c)和图6(d)依次为LOAM算法在场景3(a)中的道路a、b、c、d的建图结果，试验结果显示，LOAM算法在图6(a)中矩形圈出来的路段无法正确匹配，在图6(b)、图6(c)和图6(d)中大部分路段都无法正确匹配。图6(e)、图6(f)图6(g)和图6(h)依次为LOAM算法在场景3(b)中的道路e、f、g、h的建图结果，试验结果显示，LOAM算法在图6(e)、图6(f)和图6(g)中矩形圈出来的路段无法正确匹配，在图6(h)中可以正确匹配。由于LOAM算法在场景3(a)中的大部分路段无法正确匹配，导致测量的道路坡度无法输出正常值，所以场景3(a)的对比试验结果中不加入LOAM算法，而在场景3(b)中，只有部分路段无法正确匹配，测量的道路坡度可以输出正常值，所以场景3(b)的对比试验结果中加入了LOAM算法。

图7(a)、图7(b)、图7(c)和图7(d)依次为场景3(a)中的道路a、b、c、d的对比试验结果，图7(e)、图7(f)图7(g)和图7(h)依次为场景3(b)中的道路e、f、g、h的对比试验结果。横轴表示每次试验的里程，纵轴表示对应里程的道路坡度。其中红色曲线为在车辆运动过程中以GKSRD方法的提取频率直接实时读取的INS的俯仰角，蓝色曲线为GKSRD方法提取的道路坡度，青色曲线为LOAM算法测量的道路坡度，绿色曲线为采集的道路坡度真值。分析图7(a)、图7(b)、图7(c)、图7(d)、图7(e)、图7(f)、图7(g)和图7(h)可以发现8张图中的道路坡度变化范围都比较大，坡度绝对值最小为0°，最大可以达到11°，同时GKSRD方法与真值的拟合程度最高。分析图7(e)、图7(f)、图7(g)和图7(h)可以发现大部分LOAM的测量结果误差与直接实时读取的INS的俯仰角的误差相近，而前者在部分路段的误差要比后者更大。对比图7(a)、图7(b)、图7(c)、图7(d)与图7(e)、图7(f)、图7(g)和图7(h)，可以发现图7(e)、图7(f)、图7(g)和图7(h)中的曲线波动更剧烈，也验证了场景3(b)的道路更加不平整，同时，图7(e)、图7(f)、图7(g)和图7(h)中通过直接读取INS的俯仰角作为道路坡度的误差比图7(a)、图7(b)、图7(c)、图7(d)更大，但是本文提出的GKSRD方法在两个场景中的误差是稳定的，说明GKSRD方法具有较强的环境适应性。

表3列出了INS俯仰角作为道路坡度、LOAM测量道路坡度和利用GKSRD方法提取道路坡度在8组试验中的平均误差和最大误差。观察表中数据，可以发现INS俯仰角作为道路坡度在所有试验中的平均误差都大于0.07°，LOAM测量的道路坡度在所有试验中的平均误差都大于0.1°，而GKSRD方法在所有试验中的平均误差都小于0.01°，INS俯仰角在所有试验中的最大误差都大于1.6°，LOAM测量的道路坡度在所有试验中的最大误差都大于2.0°，而GKSRD方法在所有试验中的最大误差都小于0.5°，说明本文提出的GKSRD方法精度更高，同时具有较强的稳定性。

表3 3种方法在8组试验中的误差

图6 LOAM建图结果Fig.6 Results of LOAM

图7 道路坡度离线提取结果Fig.7 Extracted off-line result of road slope

3 结论与展望

露天矿山道路坡度大，不平整，目前的一些方法在提取露天矿山道路坡度时精度比较低，本文针对目前存在的挑战提出了GKSRD方法，该方法在很大程度上减小了由于道路坡度大和不平整导致的道路坡度测量误差。相比于目前的一些方法，GKSRD方法的精度更高，稳定性和环境适应性也更高。但是GKSRD方法存在几个不足：不适用于拐弯小，左右倾斜程度大的道路；未考虑多传感器的时间同步；真值获得效率很低。在未来的研究中，会考虑露天矿山道路的一些极端情况，同时进行多传感器的时间同步，并且寻找更好的真值获得方法。