变系数线性微分方程的解法探究

钱志祥

(广东理工学院 基础课教学研究部，广东 肇庆 526100)

对于一般的n阶变系数线性非齐次微分方程：

(1)

其中：pi(x)(i=1,2,…,n),f(x)是在某区间I上的连续实函数，若已知其对应的齐次微分方程：

(2)

的基本解组为：y1(x),y2(x),…,yn(x),x∈I,即已知(2)的通解为y(x)=c1y1(x)+c2y2(x)+…+cnyn(x),x∈I,则可利用常数变易法求得(1)的通解.但是变系数线性齐次微分方程(2)至今还没有一般的通用解法，甚至当n=2时，即2阶变系数线性齐次微分方程解法也没有一个万能的方法，目前《常微分方程》[1-3]教材中也没有系统地归纳总结出这方面的解题规律，只零星地介绍了对某些类型的微分方程有效的解法，为了探究变系数线性微分方程的解法技巧，笔者把教学过程中常用的一些特殊有效的解法和一些常规的解题方法归纳总结如下，希望逐步积累解变系数线性微分方程的经验，探究解变系数微分方程的规律.

1 变量替换法

许多特殊类型的变系数线性微分方程，通过适当的变量替换后可以化为常系数线性微分方程来求解.

定理1形如

(3)

的方程称为欧拉方程，其中a1,a2,…,an都是常数.它是一类特殊的变系数线性微分方程，这种类型的方程通过变量替换：x=et，x>0后，都可以化为常系数线性齐次微分方程.

证明作变量变换x=et，x>0，则有

用数学归纳法证明：对于一切正整数n都有

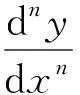
(4)

成立，其中β1，β2，…，βn-1都是常数.于是

(5)

将上述关系式代入方程(3)中，得到常系数齐次线性微分方程：

(6)

其中b1，b2，…，bn-1都是常数.

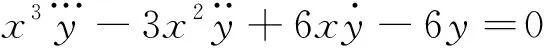
解作变换x=et，x>0，则有

将上述等式代入原方程得

(7)

而方程(7)的通解为

y=c1e3t+c2e2t+c3et.

再将t=lnx代入上式得原方程通解为

y=c1x3+c2x2+c3x.

注1所有的欧拉方程通过变量替换x=et，x>0，都可以化成常系数线性齐次微分方程来解，其他类型的变系数微分方程有的可以利用恰当的变量替换化为常系数线性齐次微分方程来解，也有的类型可以通过变量替换法降阶后来解.总之，变量替换法是微分方程求解中最常用的方法，也是其他解法的基础.

2 降阶法

定理2型如

(8)

的方程称为n阶线性齐次微分方程，若y1(x)是它的一个非零解，则可利用线性变换y=y1z将它化为n-1阶齐次微分方程.

证明作线性变换y=y1z，由莱布尼兹公式得

将上述等式代入方程(8)，方程(8)变为：

(9)

整理得

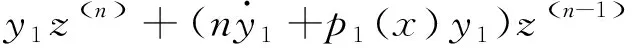
(10)

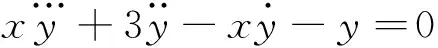
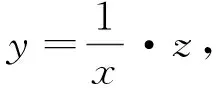
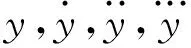
(11)

z=c1ex-c2e-x+c3.

所以原方程的通解为

注2n阶线性齐次微分方程一般都是经过适当的线性变换降阶求解或变为常系数线性齐次微分方程求解，另外这种类型的方程也可以利用刘维尔公式进行降阶求其通解.

3 拉普拉斯变换法

应用拉普拉斯变换可以求解一些变系数齐次微分方程，它主要是利用拉普拉斯变换的微分性质，具体的方法步骤如下：

(1)对线性微分方程两边取拉氏变换，把微分方程转化为含像函数F(p)的变换方程；

(2)求解变换方程，得出系统输出变量的象函数表达式；

(3)将输出的象函数F(p)的表达式展开成部分分式；

(4)对部分分式进行拉氏逆变换，求出微分方程的解析解；

(5)必要时进行验证.

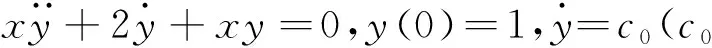
解设F(p)=L[y(x)],对方程两边同时取拉普拉斯变换得

即

整理得

两端积分得

F(p)=-arctanp+C.

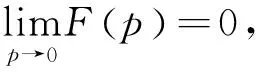
又因为

所以，当a=1时，

于是，对方程F(p)=L[y(x)]两端同时反演可得

注3拉普拉斯变换也只能解决部分变系数微分方程的解，当像函数F(p)的微分方程无法解出F(p)时，此方法失效，但是拉普拉斯变换在解常系数微分方程时不失为一种非常有效的方法.

4 刘维尔公式法

(12)

证明见文献[1].

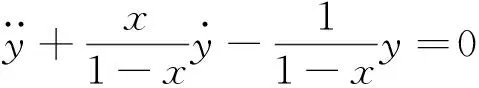
根据刘维尔公式(12)有

这是一个关于y的一阶线性微分方程，易求得它的通解为

取c=0，得特解为

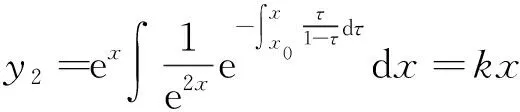
易知y1(x)与y2(x)是线性无关的，从而可得原微分方程的通解为y=c1ex+c2x(c1,c2为任意常数).

注4由刘维尔公式可知，只要知道变系数线性齐次微分方程的一个非零解，就可以求得其通解，但是如何求出变系数线性齐次方程的一个非零解，其实是十分困难的，这说明刘维尔公式法的作用也是有限的.

5 常数变易法

如果求出变系数齐次线性微分方程的解，那么就可以通过常数变易法求出对应的非齐次线性微分方程的通解[1].下面介绍二阶变系数非齐次线性微分方程的常数变易法.

设二阶变系数非齐次线性微分方程为

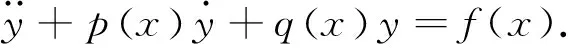
(13)

Y=c1y1(x)+c2y2(x).

设y=c1(x)y1(x)+c2(x)y2(x)是方程(1)的一个解，于是

(14)

令

(15)

(16)

(17)

将(16)、(17)代入到方程(13),得

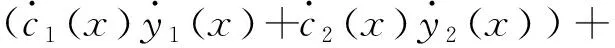
因为y1(x)和y2(x)是对应的齐次线性微分方程的解，所以

于是得方程组：

上述方程组有唯一解，记作：

所以

故微分方程(13)有特解：

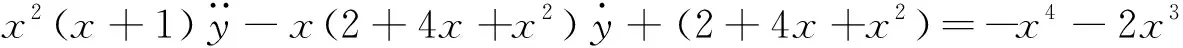
解易知对应的齐次方程的一个特解为y=x.再利用刘维尔公式(12)可求得对应齐次方程的通解为y=(c1+c2xex)x.

下面来求已知方程形如y(x)=c1(x)x+c2(x)x2ex的特解，利用常数变易法，得到方程组：

解之得，

所以原方程的通解为

y(x)=c1x+c2x2ex+x2.

注5至于高阶变系数非齐次线性微分方程的常数变易法与二阶类似，这里不再叙述.

6 幂级数解法

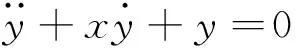
(18)

即

(19)

令x的同次幂系数为零，得

2a2+a0=0,3·2a3+2a1=0,…,n(n-1)an+(n-1)an-2=0(n≥4).

从而有

即有

所以，原方程的通解为

即

注6当微分方程的解不能用初等函数或其积分表达，而且其系数满足一定的收敛条件时，常用幂级数解法.

7 广义幂级数解法

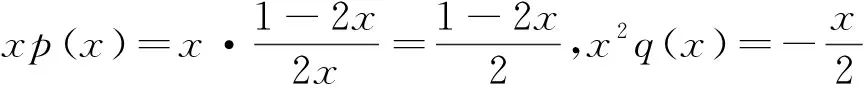
(20)

由此得到

从而得到原方程的一个解

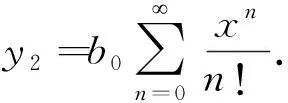
注7广义幂级数解法，对微分方程系数的收敛性要求更高.

8 勒让德函数法

定理6二阶变系数线性微分方程：

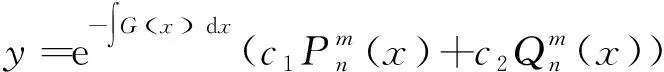
证明作变换

(21)

将它及其一阶导数和二阶导数代入原方程,经过化简便得到一个以u(x)为未知函数的连带的勒让德方程：

(22)

方程(22)的通解为

(23)

即

将(23)代入(21)便得原微分方程的通解为

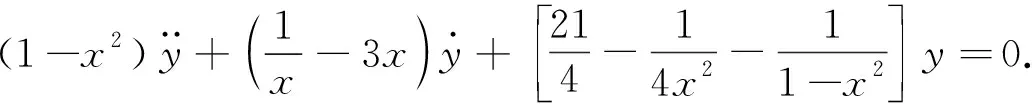
解将方程变形为

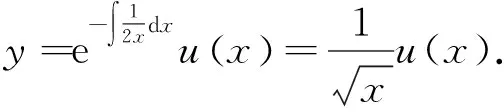
由于n=2,m=1,根据式(23)得方程的通解为

其中c1,c2为任意常数，

注8其他连带的勒让德方程的通解均可以用勒让德函数来表达.

9 贝赛尔函数法

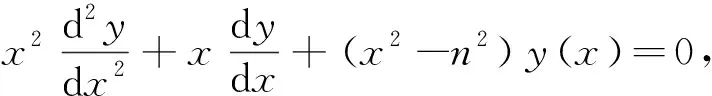
(Ⅰ)y(x)=AJn(x)+BJ-n(x)(n不为整数)；

(Ⅱ)y(x)=AJn(x)+BYn(x)(n为任意数)；

其中,定义

(Γ(x)是伽马函数)为n(-n)阶第一类贝赛尔函数；

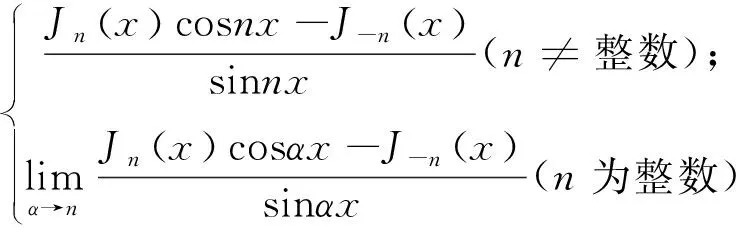
为n阶第二类贝赛尔函数；

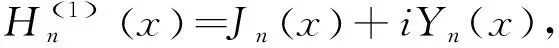
(其中i为虚数单位)为第三类贝赛尔函数.

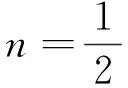
所以此贝赛尔方程的通解为

这里c1,c2为任意常数.

注9其他类型的贝赛尔方程的通解可以类似地用贝赛尔函数来表达，这里不再列举.

10 结语

变系数线性微分方程的解法还有很多种，如莱布尼兹公式法、分离变量法、特征根方程法、比较系数法、积分方程法、数值解法等[8-9]，这些解法都有一定的局限性，本文不再阐述.总之，变系数线性微分方程的解法繁多，但是没有一种解法是通法，所以需要读者在长期的解题实践中逐步积累经验，不断地探究变系数线性微分方程的解题规律.