地球同步轨道目标物深度学习检测方法
黄西尧,何羿霆,杜华军,曾祥远,刘天赐,单文婧,程 林
(1. 北京理工大学自动化学院,北京 100081;2. 北京航天自动控制研究所宇航智能控制技术国家级重点实验室,北京 100854;3. 北京航空航天大学宇航学院,北京 102206)
0 引 言
欧洲空间局先进概念组(European space agency advanced concepts team)发起一项面向全世界的科技竞赛:Spot the GEO satellites(简称SpotGEO),竞赛时间为2020年6月7日至8月31日(UTC时间)。主办方给定了由低精度传感器观测一定区域天空并拍摄的连续五帧图像,竞赛任务是基于五帧图像精确识别位于地球同步轨道(Geostationary orbit, GEO)及其附近的卫星或空间碎片(目标物)。全数据集共计6400个图像序列,分为训练集1280个序列和测试集5120个序列,其中训练集提供标定数据[1]。每个序列包含五帧图像,每帧图像拍摄过程中传感器保持静止,曝光时间约为40秒;同一个序列相邻两帧之间传感器发生微小旋转,保证2帧图像具有公共区域。受地球自转和拍摄方式影响,恒星在图像中将呈现线条状图案,而目标物呈点状图案(见图1)。某些位于GEO附近区域的目标物,可能呈现为拖曳状图案。区别于含有仪器型号、参数设置等丰富信息的FITS数据格式,比赛数据采用PNG格式,分辨率为640×480。得分和均方误差(Mean square error, MSE)是本次比赛的两个主要评价指标,具体计算方法见第3节。
基于光学望远镜的GEO物体检测可用于空间碎片观测、卫星碰撞预警等方向[2]。传统检测方法常需要大口径望远镜,高分辨率、低噪声CCD传感器,成本较高[3]。天基观测能够有效避免天气和大气因素的影响[4-5],其缺点为观测平台搭建困难、造价高昂。因此,利用低成本、低精度的地面观测设备实现对较大空域的长时间监视具有积极的研究意义。然而,观测距离远,图片分辨率低,云层、恒星遮挡,大气影响,光污染以及传感器噪声将为目标物的精确识别带来困难,这也是本次竞赛的主要难点。
根据成像形态不同,空间目标检测方法可分为点状目标检测和拖曳状目标检测。本文主要介绍作者于竞赛中关注的点状目标检测方案,拖曳状目标检测可参考文献[6-7]。受地球自转和拍摄方式影响,目标物在星空背景下呈现近似直线排列特征[8]。因此,主流方法先处理单帧图像,即分割前景(目标物、恒星等)和背景(噪声、空间背景等)图像;后利用GEO物体匀速直线运动特性,识别图像中有效目标物。图像前/背景分割环节中,通常先根据目标物频域或空间域特征,增强其在图像中的强度;后进行二值化处理[9]。常见的目标增强方法有高斯过程回归[10]、形态学滤波[11]和点扩散函数反卷积[12]等。二值化处理后,图像冗余信息显著减少,可用于GEO物体的检测。文献[10]采用遍历所有点对的直线检测算法,时间复杂度过高。为提升计算效率,文献[13]引入随机抽样一致方法(Random sample consensus, RANSAC)。Liu等[14]提出基于拓扑扫描的直线特征提取算法,计算效率和鲁棒性较高。上述算法均采用较高精度数据集,对于低精度图像,严重的噪声污染、欠采样等现象可能引起目标物误判等问题。此外,检测前跟踪(Track before detect, TBD)方法[15-16]也被应用在空间小目标检测任务中,该方法需要依靠较长的图像序列以满足轨迹预测,并不适用于短序列数据集(本次竞赛数据集每个序列只包含五帧图像)。
近年来,深度学习逐渐应用于目标检测研究工作。根据候选区域的提取与否,基于深度学习的目标检测方法可分为两阶段法和单阶段法[17]。两阶段法先提取候选区域,再通过对区域分类实现目标检测。RCNN[18]采用选择性搜索(Selective search)提取候选区域,卷积神经网络提取每个区域的特征,SVM对特征分类。Fast RCNN[19]和Faster RCNN[20]分别改进了特征提取,特征分类和候选区域提取方法。相比之下,单阶段法直接对图像进行卷积特征提取,在特征图上得到目标边框,检测速度快。YOLO[21]将图片划分成网格,直接计算每一个网格的预测结果。深度学习检测方法未利用GEO物体的匀速直线运动特征,加之GEO目标物在图中占像素量少,直接使用上述两类方法将带来训练样本不平衡、预测精度低等问题。
综上,针对低精度图像数据,本文提出一种基于深度学习的GEO目标检测改进方法。第一步,通过高斯过程回归提取图像的前/背景,完成图像二值化。第二步,使用模板匹配方法实现图像配准,并删除重复区域。第三步,根据Liu方法[14]提取图像序列中具有匀速直线运动特征的目标物。为减小噪声干扰,提高扫描效率,在拓扑扫描前使用卷积神经网络进行第一次筛选,删除概率较低的候选目标物。扫描结束后,再次利用卷积神经网络对拓扑扫描结果进行分类,实现高精度的目标物检测。
全文内容安排如下:引言部分介绍竞赛问题与研究现状;第一节介绍包括前景/背景分割和图像配准在内的准备工作;第二节介绍拓扑扫描直线检测算法,并给出作者基于深度学习的目标物筛选新方法;第三节给出实验及对比结果,总结并指出值得改进之处。
1 准备工作
本文目标物检测方法分为三个部分:前景/背景分割、图像配准和轨迹检测。其中,第一、二部分为准备工作。图像配准结束后,各帧存在的候选目标物被转换至公共坐标系中,作为第三部分的输入。在第三部分拓扑扫描方法前后,各进行一次基于深度学习的候选目标物筛选工作,最终得到真实目标物坐标。方法具体流程如图2所示。
1.1 前景/背景分割
采用高斯过程回归(Gaussian process regression, GPR)[22]方法进行图像分割,将原始图像分成前景(目标物和恒星条纹等)和背景(噪声和空间背景等)。算法的主要内容为:假设原图中某像素点灰度y(xi)对像素坐标xi满足
y(xi)=y*(xi)+μi
(1)
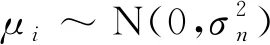
y*~N(0,K)
(2)
式中:K∈RN×N为协方差矩阵。高斯过程回归的主要思想为利用贝叶斯推理,从原图灰度值(后验概率)估计前景、背景灰度值(先验概率),假设待估计像素坐标为xpre,则对应像素坐标位置灰度值(先验概率)应为
ypre=kT(xpre)(K+σnI)-1y
(3)
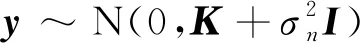
M(xi)=ypre,FG(xi)-ypre,BG(xi)
(4)
以训练集第143号序列为例,利用高斯过程回归方法分离前景、背景,并获得前景掩码(如图3所示)。相对于全局二值化,局部自适应二值化能够更好处理背景变化较大的图像情况,在本次竞赛中反映为云层、光污染等影响。因此,本文使用Opencv中自适应二值化函数对前景掩码进行二值化处理,其主要思想为:用滑动窗口遍历整个图像,每次仅对窗口内的区域进行二值化处理。阈值可以是该区域某些灰度统计值(实验中取该区域内灰度值的均值加常数)。利用恒星条纹进行图像配准(配准方法见1.2节),为消除恒星条纹的影响,将连续五帧二值化图像转换至公共坐标系,删除具有交集的图像区域(即将灰度值置零)。进行连通区域分析,用中心点代替整个连通区域,实现对图像离散化处理。至此,一个序列五帧原始图像被转化为公共坐标系下的一张散点图,每个点包含像素坐标和时间(帧号)信息。

图3 图像的前景、背景和前景掩码Fig.3 The foreground, background and foreground mask of the image
1.2 图像配准
采用Opencv中模板匹配算法实现图像配准,其核心思路为在目标图像中找到与待匹配图像最相似的区域。为提高准确率,需要对图像进行滤波处理,保留恒星条纹,减少噪声对配准效果的影响。图像配准具体步骤如下:
1)使用同态滤波和均值滤波处理原始图像,使图像中仅保留恒星条纹。
2)拓展图像边缘,用灰度值为0的像素点填充(确保原始图像边缘部分不因图像位置变换而丢失)。
3)截取待匹配图像中心区域(文中选取宽和高的1/3)。
4)使用模板匹配函数,计算待匹配图像中心区域在目标图像的最佳匹配位置。
5)计算待匹配图像到目标图像的变换矩阵。
设第一帧到第二帧变换关系为:
PI2=H12PI1
(5)
式中:PI1,PI2分别表示P点在第一帧和第二帧下像素坐标矢量,H12表示第一帧到第二帧变换矩阵,以此类推。以第五帧图像坐标系为基本坐标系,为提高匹配精度,即增大模板匹配算法输入图像公共区域,本文分别计算相邻两帧变换矩阵,则第一帧到第五帧图像变换关系为:
PI5=H45H34H23H12PI1
(6)
综上,某序列五帧图像对齐后结果如图4所示(图像经过插值处理,图中由目标物形成的近似直线轨迹已圈出)。

图4 图像配准效果图Fig.4 The result of image registration
2 基于深度学习的改进目标物检测方法
2.1 对偶空间及拓扑扫描算法
由于目标物在配准后的图像上呈等间距直线排列,可利用直线提取算法进行检测。Liu等[14]基于拓扑扫描,提出了一种高效而低参数敏感性的新型多目标跟踪方法。然而,该方法未考虑多线交于一点的退化情况下目标物检测方案,无法处理低精度图像序列中噪声引起的输入点数量过大且分布集中的问题。因此,本节基于Liu方法,介绍拓扑扫描方法基本原理,给出退化情况下目标物检测解决方案。
对于输入点集M中某点PA(xA,yA,tA),xA和yA分别表示横纵坐标值,tA表示该点所属帧号(如图5左所示,图中未标出帧号)。取容忍范围ε,将点PA沿y轴分别上下平移ε,获得点对{P′A(xA,yA+ε),P″A(xA,yA-ε)}。令连接两点形成的竖直线段为点对中间区域,当存在某条直线同时横穿多个点对中间区域,则认为对应点在同一直线上(如图5右所示)。

图5 原始空间内点对示意图Fig.5 Diagram of point-pair in the primal space
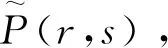
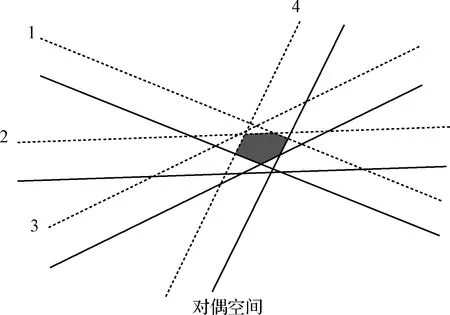
图6 对偶空间中点对及拟合直线表现形式Fig.6 Point-pair and fitting line in the dual space
遍历所有封闭区域,可获得所有形成直线的点集。由于目标物做近似匀速直线运动,为找到它的运动轨迹,需要分别扫描(x-y)和(x-t)空间中的直线。为高效且准确完成遍历工作,Liu等基于拓扑扫描方法进行搜索,取得了较好的效果,整个算法计算复杂度为O(n2),算法主要流程如图7所示。
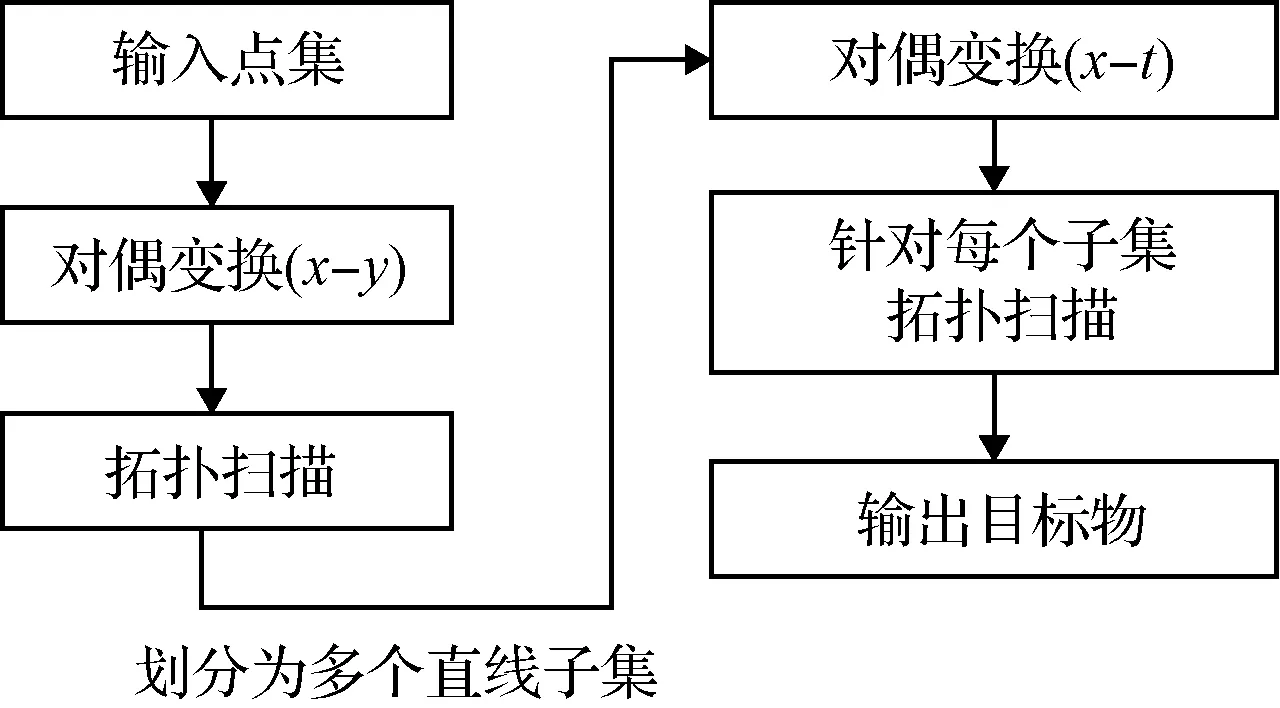
图7 基于拓扑扫描算法的目标物检测流程图Fig.7 Flow chart of the target object detection based on the topological sweeping algorithm
经典拓扑扫描算法中,当扫描线切割的连续两条线段具有相同右端点时,进行一次更新操作。更新操作结束后,扫描线从该右端点左侧扫描至右端点右侧。因此,每次更新仅涉及到两条线段所在直线的相关信息变化,而不影响其他直线的状态(如图8(a)所示)。当扫描线切割的所有线段均不存在相同右端点时,整个拓扑扫描结束,实现了全平面所有线段的遍历工作。为进一步探究每次更新对封闭区域的影响,以第i条与第i+1条线段为例:更新前后,两条线段位置关系发生变化(更新前第i条线段在第i+1条上方,更新后相反),两条线段与其形成的一个相关区域(浅色部分)位置关系也随之改变,而其他线段位置关系不变。因此,每次更新前后只需要判断对应的相关区域,即可完成对整个对偶空间封闭区域的无遗漏且无重复遍历工作。具体算法及数据结构见文献[14]。
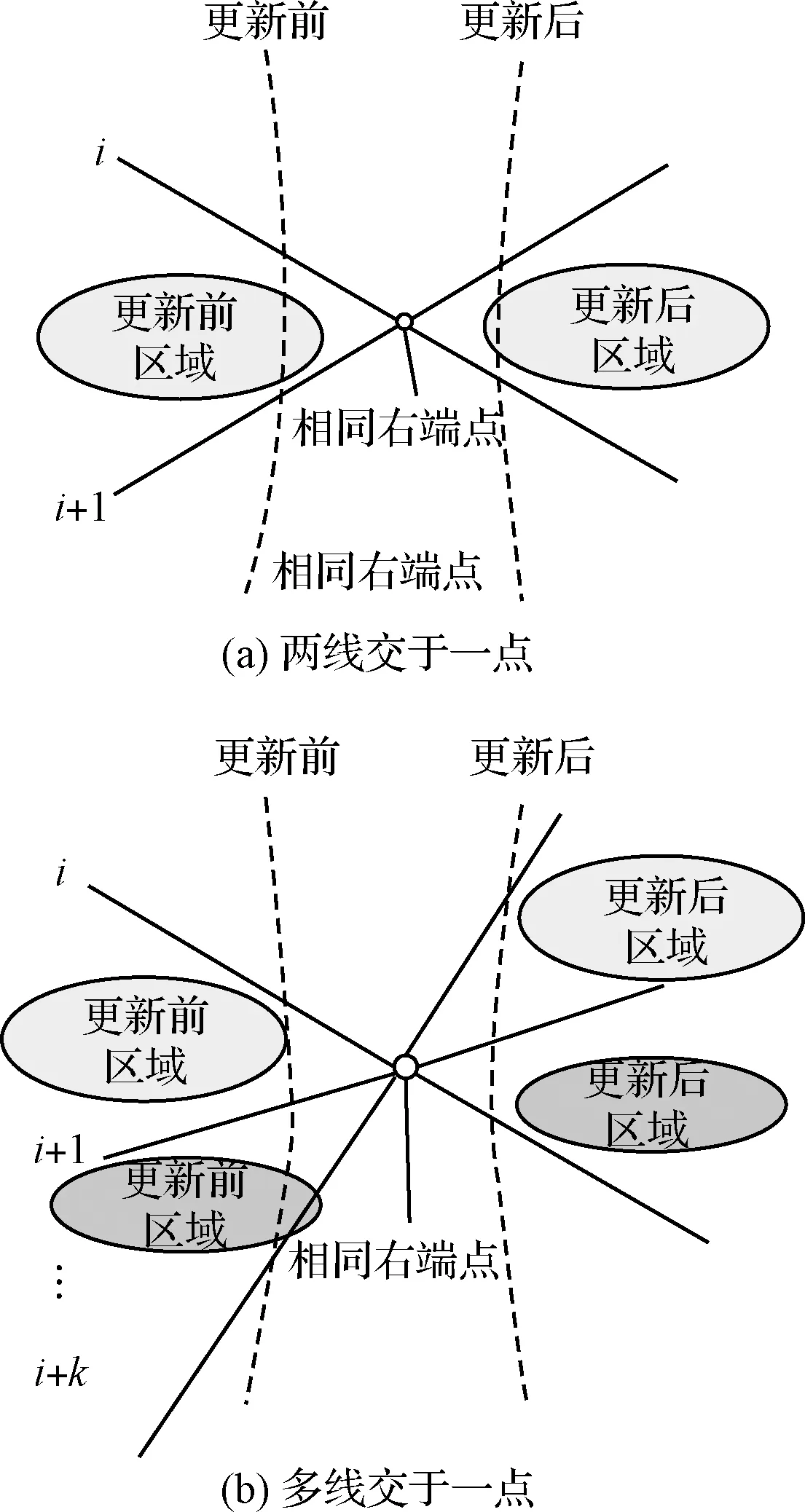
图8 拓扑扫描及其退化情况更新方法Fig.8 The update method based on the topological sweeping and the degenerate case
当输入点数量较多时,对偶空间内对应直线往往存在多线交于一点的退化情况(如图8(b)所示)。每次更新前后,多条线段及相关区域的位置关系发生变化,原始目标物检测更新算法将不再适用。因此,本文基于拓扑扫描的退化情况的解决方案[23],提出改进目标检测算法如下:
1)当且仅当有两条线段具有相同右端点,算法同文献[14]。
2)当三条或三条以上的线段具有相同右端点,以第i+1个相关区域为例:
(1)提取形成第i+1区域的两条线段(第i条线段和第i+1条线段)的左端点λi和λi+1,以及相同右端点ρ。
(2)计算特征点坐标ν=(λi+λi+1+ρ)/3,ν点一定在该区域内部。

(5)更新直线数据(具体数据结构同文献[12])。
(6)采用文献[23]中的方法更新拓扑扫描。
值得注意的是,改进后拓扑扫描的结果可能包含某些点集的子集,如:拓扑扫描获取某组候选目标物序列{P1,P2,P3,P4},结果中同时含有序列{P1,P2,P3}和{P1,P2,P4}。为便于后续补充遗失点的操作,需要合并所有含有2个及以上相同点的候选目标物序列集合。
2.2 基于卷积神经网络的候选目标物筛选
由于光污染、云层等因素的影响,某些图像背景过于明亮、模糊,预处理后得到的输入点集包含噪声点过多,大大增加了计算成本。以约300、500和1000数量点集为例,其完成拓扑扫描的时间依次为43.5秒、139.1秒和870.4秒。同时,某些噪声点由于“巧合”满足轨迹规律而被误判为有效目标物(见图9)。图中,尽管空心圆点数量≥3且分布满足规则,事实上这完全由噪声点组成。仅仅依靠拓扑扫描技术无法区分此类结果,严重影响了目标物识别的准确性。因此,本文依靠深度卷积网络,将拓扑扫描的输入数据和输出结果看作候选目标并进行筛选,有效提高了直线扫描效率及最终结果的准确率。
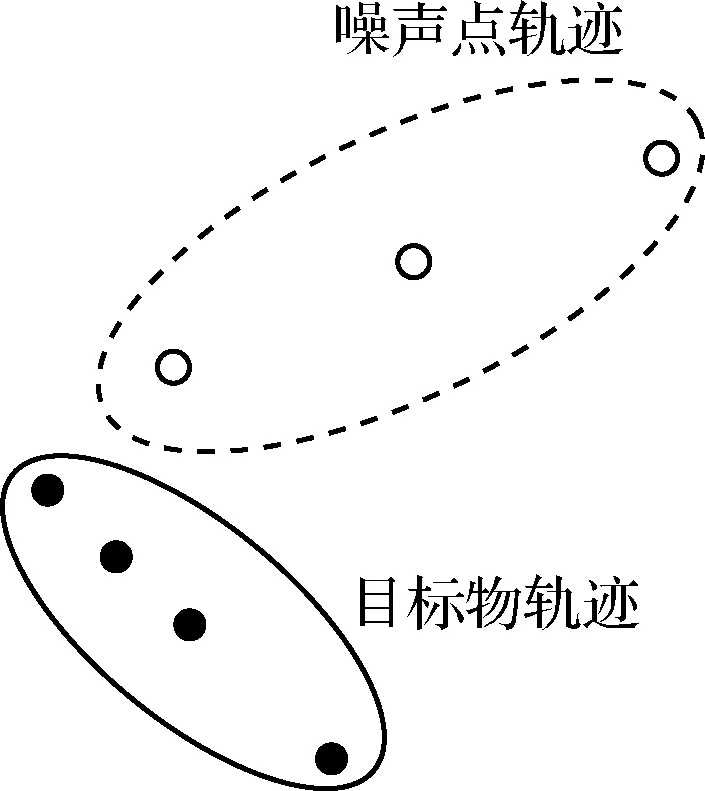
图9 目标物、噪声轨迹示意图Fig.9 The diagram of target object and noise tracks
2.2.1训练数据预处理
像素事件检测方法[13]的基本思想为:连续观测某一固定星空背景区域,当目标物经过时,该背景对应图像区域的灰度值将出现显著的特征变化,由此判断候选目标物的存在。基于该思想,使用神经网络对目标物的出现情况做出判断。以连续五帧相同背景区域大小为28×28的灰度图像作为一组输入数据。该数据分为两类,一类使目标物在其中一帧能够被有效观测(即未被恒星条纹遮挡等,如图10所示),另一类完全不包含目标物。具体数据处理方法如下:
1)利用标注文件,分别提取各帧内被有效保留的目标点像素坐标。
2)以该目标点为中心截取28×28的图像。
3)利用变换矩阵,截取其他帧中具有相同背景空间的图像;整合五帧数据,将数据标签记为1。
4)同理获取一系列不包含有效目标物的五帧图像数据,标签记为0;为确保样本数量均衡,标签为1与标签为0的数据数量比为1∶1。

图10 神经网络输入数据(仅左侧第一帧包含目标物)Fig.10 The input of the neural network (only the first frame contains a target object)
2.2.2卷积神经网络模型及训练结果
使用的网络由2个卷积层、2个最大池化层、4个全连接层以及1个softmax层组成,激活函数为ReLU,目标函数为Cross Entropy,优化器为Adam。由于目标尺寸较小,卷积核统一采用尺寸3×3,步长1的结构,保持卷积层输出尺寸不变;池化层采用尺寸2×2,步长2的结构。网络的输入部分需要减去训练集图像的灰度平均值。网络的输出分别为判断该点是有效目标物的概率ωt和不是有效目标物的概率ωf。由于样本数据较少,为防止过拟合,在全连接层之间使用了Dropout正则化方法[24]。训练过程中,Dropout可随机断开部分神经元之间的连接,增加网络模型的随机性,防止过拟合。各层参数细节见表1。

表1 卷积神经网络结构Table 1 Convolution neuralnetwork structure
将训练集前200个序列保留作为测试集。将第201到1280号序列按照0.85∶0.15比例随机选取分成训练集和验证集。各项参数设置为:初始学习率0.0001,批大小为50,迭代次数60轮。测试所用设备为Intel(R) core(TM) i7-10700F CPU 2.90 GHz GeForce RTX2060 5931MB。训练过程中,每轮迭代后记录对训练集的平均训练误差和对验证集的平均验证误差,二者的变化如图11所示。随迭代轮次增加,训练误差和验证误差最终均能达到0.3以下且相差较小。该结果表明网络性能良好,训练集和验证集划分合理,数据分布相近。训练过程中网络对验证集的平均预测准确率变化如图12所示。预测准确率随迭代轮次增加而不断提升,训练结束时,预测准确率达到最大值93.21%。
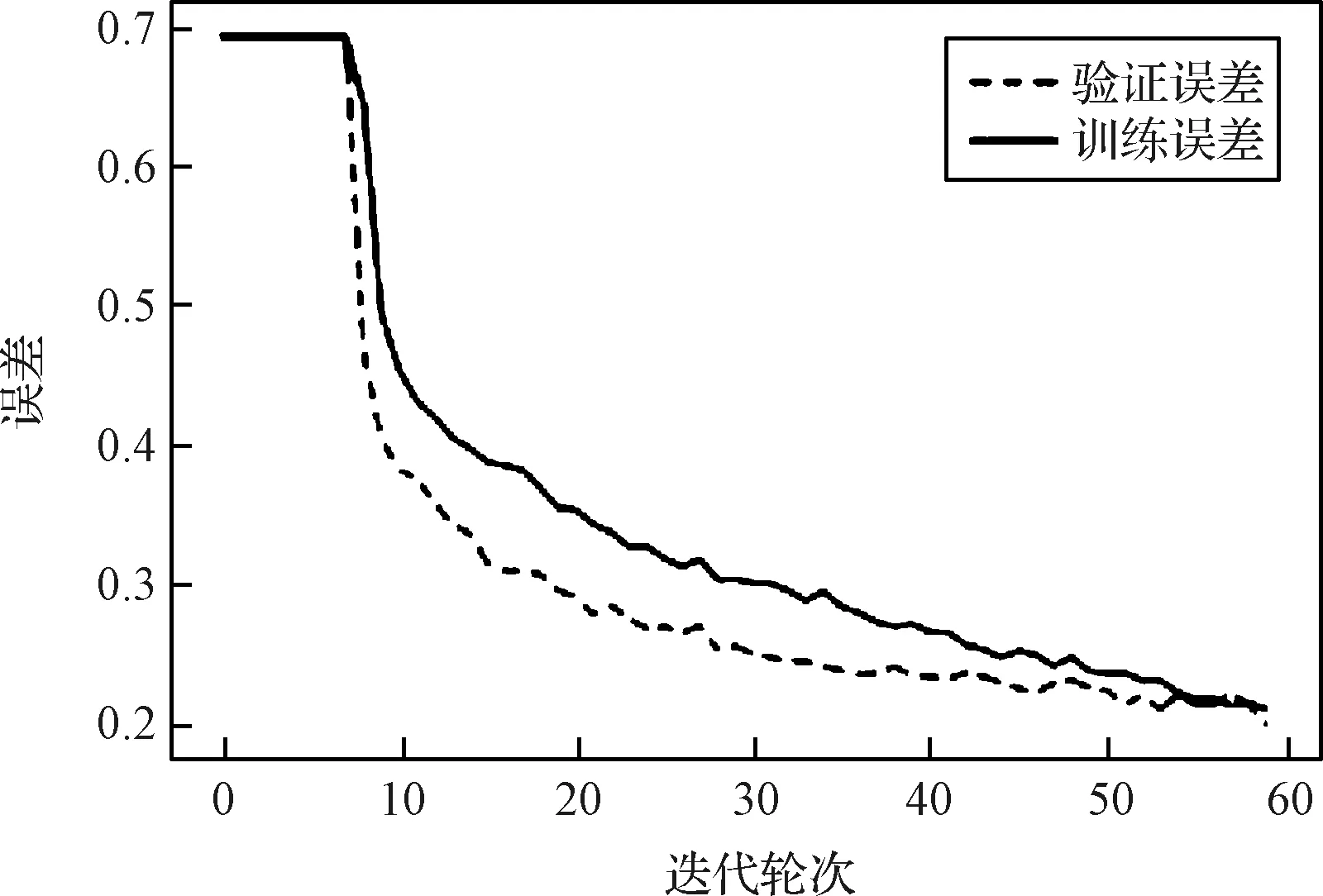
图11 训练误差随迭代轮次变化曲线Fig.11 Train loss and validation loss of each epoch
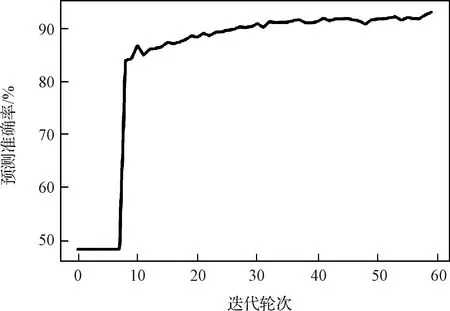
图12 预测准确率随迭代轮次变化曲线Fig.12 Prediction accuracy of each epoch
2.2.3两次卷积神经网络筛选方法
1) 拓扑扫描前的第一次候选目标筛选
针对输入点数量过大的情况进行筛选处理,以降低噪声对扫描效率的影响。利用神经网络,计算每个点是有效目标点的概率ωt,保留概率较大的一部分点。具体流程和参数设置如图13所示。
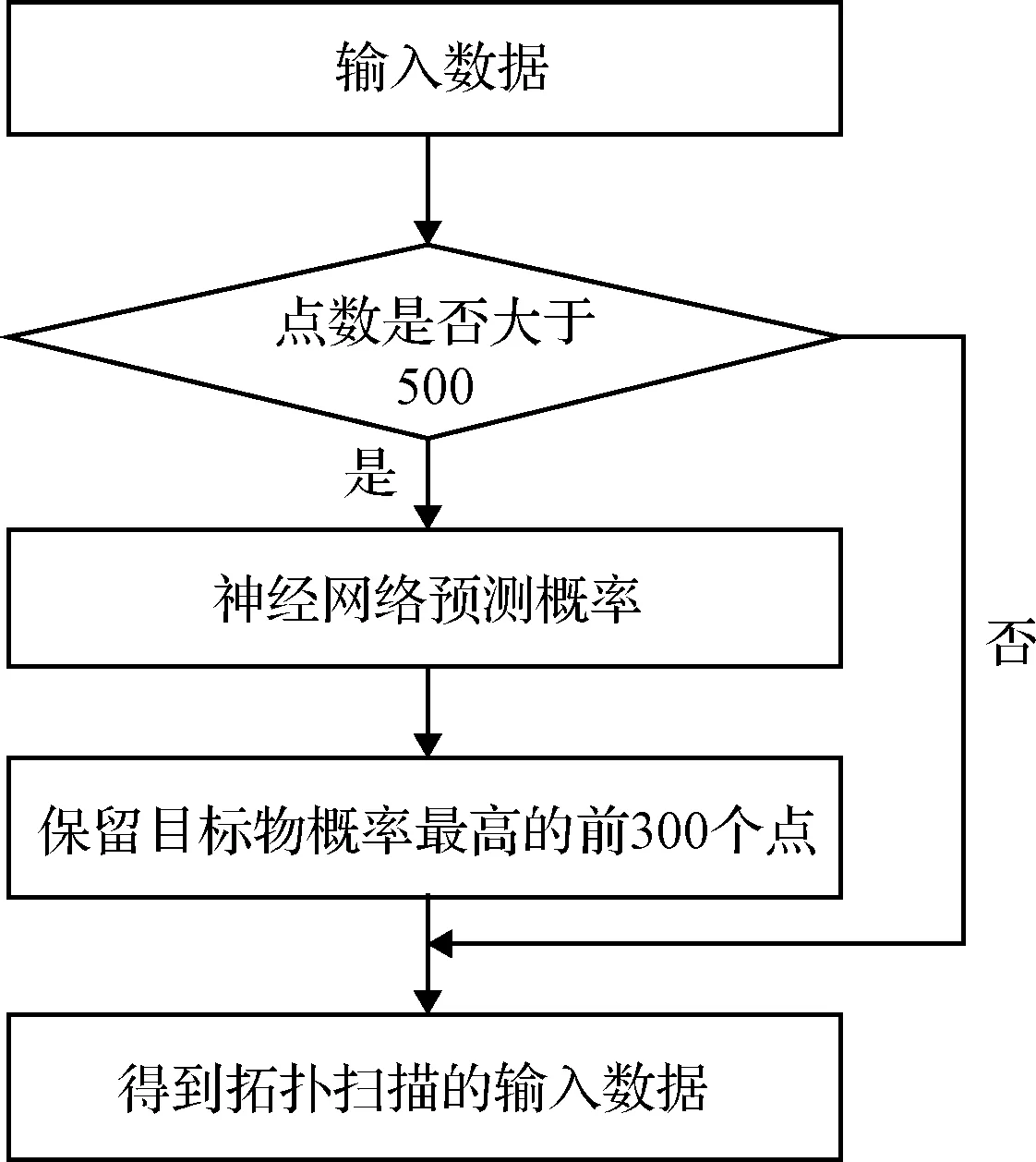
图13 拓扑扫描前数据筛选流程图Fig.13 Flow chart of the data filtering before the topological sweeping
2) 拓扑扫描后的第二次候选目标筛选
利用拓扑扫描技术,并按照直线运动规律对结果采取补点操作,获取一系列候选目标物序列。每个序列共含有5个目标点,利用卷积神经网络分别对这些目标点进行预测,当是有效目标点的概率ωt大于不是有效目标点的概率ωf时,认为该点为有效目标点,反之则为噪声。为避免误删有效目标物,提高预测准确率,规定在一个候选目标物序列中,5个点至少有3个被判定为噪声时,认为该候选目标物序列为噪声序列并删除(如图14所示,图中圆点表示该点被判定为有效目标点,叉号表示该点被判定为噪声)。
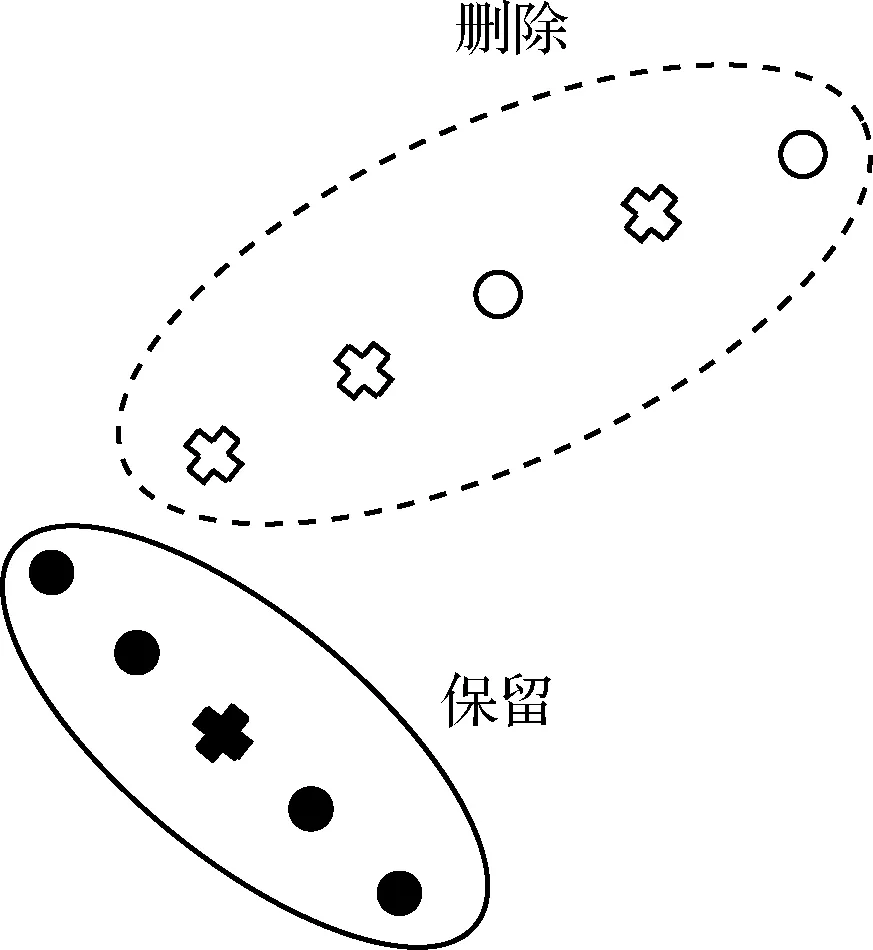
图14 拓扑扫描后的数据筛选Fig.14 Data filtering after the topological sweeping
3 实验结果
本次竞赛主办方提供训练集1280个序列的标注数据,考虑到本文使用第201到1280个序列用以神经网络训练,故对训练集前200组目标物进行检测作为实验结果。值得一提的是,根据主办方评分准则,前200组数据得分与5120组最终测试集结果得分非常接近(前者0.114659,后者0.115817),因此认为训练集前200组数据可反映整个数据集特征。
主办方采用得分Fs和均方误差FMSE作为实验结果的评价指标,其中得分为最终排名的首要依据,具体计算规则如下:
定义真阳(True positive, TP)NTP表示在一定误差范围内被准确识别的目标物数量,假阴(False negative, FN)NFN表示被遗漏目标物数量,假阳(False positive, FP)NFP表示将其他物体误判为目标物的数量。准确率α和召回率γ计算公式为:
(7)
竞赛的最终得分计算公式为:
(8)
当存在两队得分完全相同时,使用均方误差进行比较,均方误差较小的一方排名靠前。定义误差平方和(Sum squared error, SSE)FSSE为
(9)
式中:i,j,k分别为TP,FN,FP的数量,τ为主办方预设得分常数。每存在一个遗漏目标物(FN)或误判目标物(FP),为均方误差带来τ2的增量。函数ψ(i)为TP部分误差计算函数,当目标物坐标的计算值与真实值在某个限定范围内,ψ(i)=0;反之则以距离的平方作为误差。最终,均方误差FMSE可表示为:
(10)
3.1 第一次筛选结果
将第一次筛选前数据按照离散点数目划分区间,分别统计筛选前后各区间离散点总数、目标物总数,目标物保留率和目标物占比。其中,目标物占比指目标物数目占总离散点数目百分比。统计结果见表2。前200个序列中,离散点数目普遍小于500个(占82%),该部分序列无须进行筛选工作。对于
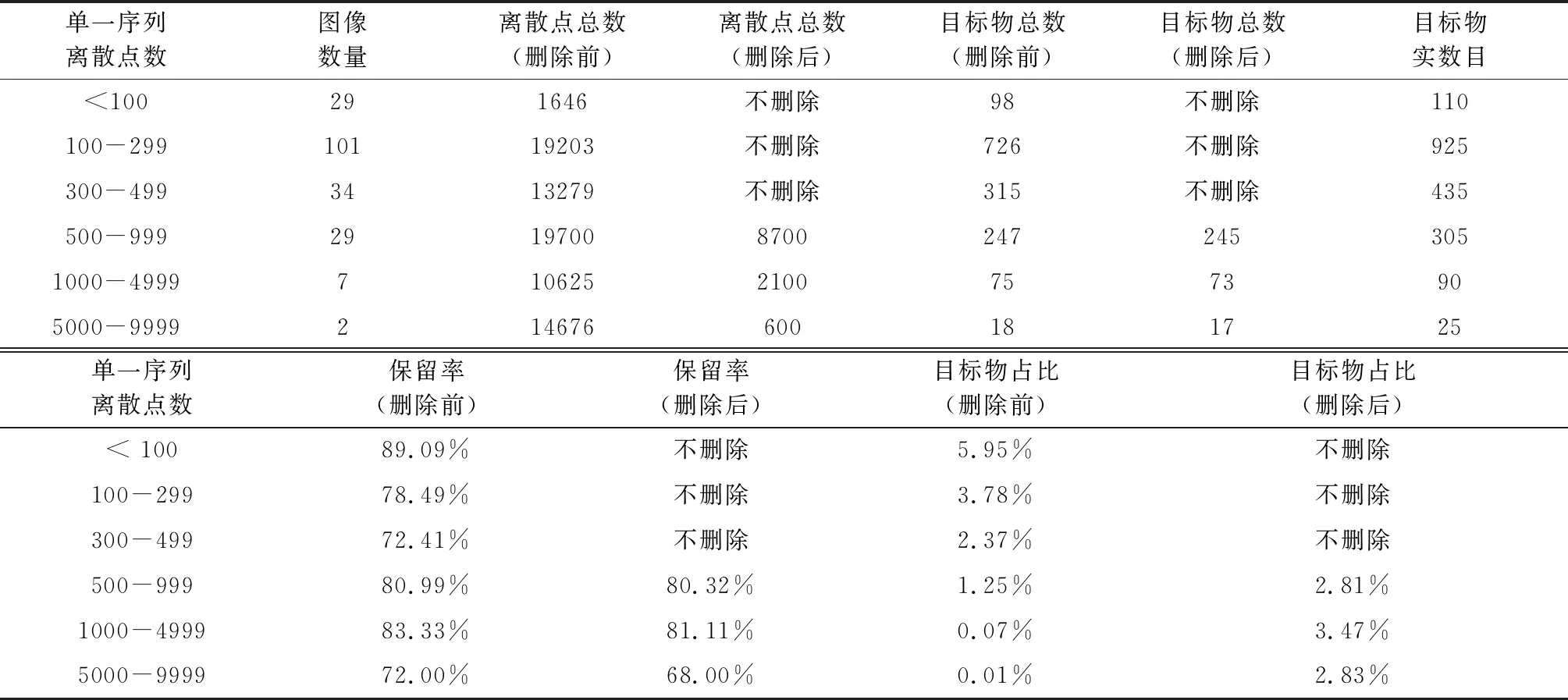
表2 第一次筛选结果Table 2 The first data filtering resulting
离散点大于500个的序列,利用神经网络进行筛选,筛选工作对目标物的误删影响非常小(对于500-999,1000-4999,5000-9999三个区间,目标物仅被误删2、2、1个)。同时,筛选前后目标物占比显著增加(从删除前1.25%、0.07%和0.01%,提升至2.81%、3.47%和2.83%),噪声点数目减小,显著缩短了拓扑扫描步骤的计算时间。
3.2 第二次筛选结果
对拓扑扫描结果进行第二次筛选,筛选前后结果相关数据见表3。第二次筛选前,数据包含有效目标物1890个(NTP+NFN),其中被正确识别的目标物为1546个(NTP),遗漏目标物344个(NFN),且存在大量误判(NFP)。经过第二次筛选,尽管20个有效目标物被误删除,但是误判(NFP)数量大幅度减少,由869个下降至仅30个,有效提升了判断的准确率,最终得分显著提升。值得一提的是,虽然神经网络的预测准确率仅为93%,由于筛选的容错性,最终准确率达到了98.07%。受比赛时间限制,该网络存在值得完善之处:如在保持小卷积核的情况下增加卷积层数,减少全连接层数,删去最后两个全连接层之间的Dropout正则化等,或将提升网络的预测精度。
本队最终比赛成绩:FMSE=62021.8092,得分Fs=0.1158,排名第五。整个比赛共有30只队伍提交结果,第一名成绩为FMSE=33838.9931,得分Fs=0.0517(成绩保留4位小数)[25]。
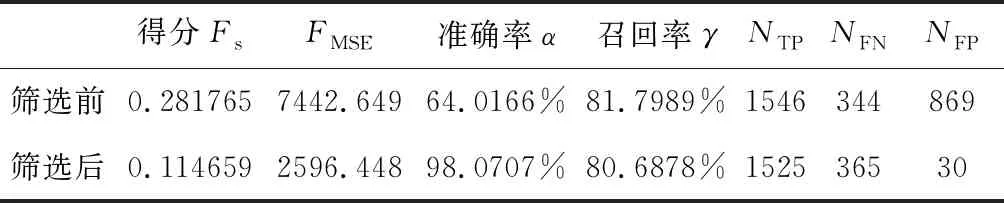
表3 第二次筛选结果Table 3 The second data filtering results
4 结 论
针对低精度GEO图像数据,提出了基于深度学习的GEO目标检测方法。改进以拓扑扫描算法为基础的GEO目标检测更新方式,使之适用于噪声点多且分布集中的低精度图像数据。增加基于深度学习的目标物筛选环节。第一次筛选将单一序列离散点数控制在500个以内,显著提升拓扑扫描的计算效率(500个点对应拓扑扫描检测时间为139.1秒,1000个点对应时间为870.4秒)。拓扑扫描后进行第二次数据筛选,以删除形成误判定的噪声序列。实验中,删除839个噪声序列,仅损失21个有效目标物,判断准确率大幅度提升(由筛选前64.0%上升至98.1%),有效提高最终成绩。
本文方法最终召回率仅为80.7%,仍存在较大提升空间。未来研究中,可根据文献[10]引入损失函数,针对不同背景环境图像选取合适的高斯过程回归参数;或选择新的图像滤波技术,提高目标物的保留率;或增加图像增强环节,突出某些过于黯淡的目标点,进一步考虑拖曳状目标物的检测方法。

