运载火箭推力故障下基于智能决策的在线轨迹重规划方法

谭述君，何 骁，张立勇，吴志刚

(1. 大连理工大学工业装备结构分析国家重点实验室，大连 116024；2.大连理工大学辽宁省空天飞行器前沿技术重点实验室，大连 116024 3. 大连理工大学电子与信息工程学院，大连 116024)

0 引 言

随着航天科技的迅猛发展，人们对运载火箭的可靠性提出了越来越高的要求。发动机作为火箭动力装置，是全箭飞行可靠性及安全性的决定性因素，其可靠性关乎整个飞行任务的成败。在实际飞行任务中，运载火箭发动机故障等原因易造成推力下降，如果继续沿用标称弹道条件下的制导控制方案将难以完成任务，会导致飞行任务部分失败或全部失败。在世界航天史上，有很多由于发动机故障导致任务失败的教训，如俄罗斯联盟-U曾因三级发动机燃料管堵塞而失去推力，最终发射货运飞船任务失败。随着自适应制导技术[1-4]的发展，一些运载火箭在发动机故障情况下，通过调整飞行程序，仍能完成入轨。德尔塔4在发射第3颗GPS-2F 卫星任务中利用制导系统重新生成飞行轨迹，对上面级发动机故障时的推力下降进行了及时补偿，充分利用剩余燃料成功地完成了卫星入轨。然而，如果故障引起的运载能力损失较大，即使延长飞行时间，依然不能将载荷送入目标轨道。

为了主动避免有效载荷的坠落，需要依据故障状态在线重规划救援轨道和飞行轨迹，使载荷进入救援轨道。近年来，箭载计算机计算性能的提高使得在线轨迹规划成为可能[5-8]。对于推力下降故障下的在线救援问题，目前主要的思路是直接求解推力故障引起的目标轨道未定的轨迹重规划问题，即优化一条轨迹使救援轨道与原目标轨道的误差最小[9-10]。文献[9]提出了一种在运载火箭推力下降故障下的自主救援策略和算法，结合入轨点地心角估计、凸优化、自适应配点法等，为重规划问题提供一个好的初值，以提高在线计算效率和收敛性。文献[10]为保证动力系统故障时的飞行安全，提出了一种基于凸优化的运载火箭在线轨迹优化算法，以得到一种高精度、高效率的在线轨迹优化方法。上述方法把最优救援轨道的决策和飞行轨迹优化两个问题耦合在一起优化，由于救援轨道的未知，最优解的搜索空间很大，大大影响在线计算效率和稳定性。对于在线轨迹优化问题，不合理的初始值会导致优化问题的计算耗时长[11-12]。若能快速地决策出最优救援轨道，为后续在线轨迹优化提供合理的终端约束，那么在线轨迹优化问题的复杂度则会大大降低，从而整体上提高在线救援的计算效率。

最优救援轨道决策需要综合考虑全箭动力学、故障信息以及轨迹规划中的过程约束和终端约束，通过求解一个目标轨道未定的轨迹规划问题得到[13-15]。其中涉及复杂的逻辑推理和众多的约束条件，是一个典型的知识处理过程，比较适合采用机器学习的方法加以解决。径向基神经网络仅用少量的神经元，就具有映射多维非线性系统的能力，具有良好的函数逼近性能[16-19]。与标准前馈反向传播网络相比，径向基神经网络具有学习速度快、陷入局部极小收敛机会小等优点[20]。

因此，本文将推力故障下的轨迹重规划问题转化为最优救援轨道的在线智能决策和成熟的燃料最优轨迹规划问题进行求解。以发生故障轨道平面内最大圆轨道作为最优救援轨道，提出推力下降故障情况下基于智能决策的在线轨迹重规划方法。本文的组织结构如下：首先介绍推力下降故障情况下的轨迹重规划问题；其次给出基于智能决策的在线轨迹规划方法；然后是救援轨道决策模型的评估、在线轨迹优化的结果与讨论；最后得出结论。

1 问题描述

以两级运载火箭为研究对象，假设推力下降故障发生在二级飞行段[21]。此时大气稀薄，可以忽略气动力影响。定义地心惯性坐标系：原点在地心，X1轴在赤道平面内指向发射时刻本初子午线方向，Z1轴垂直赤道平面指向北极，Y1轴满足右手定则。在地心惯性坐标系中建立火箭的上升段二级飞行动力学方程如下：

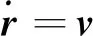
(1)

(2)

(3)

式中:r，v为运载火箭的位置、速度向量。μ为地球引力常数，m是火箭的总质量，Isp为火箭的发动机比冲。u=[ux,uy,uz]T为发动机的推力单位矢量分量，是可控的。当发动机发生故障，推力下降的比例是η，推力大小是(1-η)Tnom,Tnom是发动机标称推力。推力下降故障情况下，发动机比冲不变，推进剂的秒耗量也下降η，总飞行时间可以超过标称的飞行时间。下文所有计算都是以式(1)～(3)作为状态方程，包含7个状态量x=[rT,vT,m]T和3个控制量u=[ux,uy,uz]T。

假定发动机推力下降故障出现时刻为t0,运载火箭需要以t0时刻的状态为起始点进行轨迹重规划，因此起始点等式约束条件可表示为:

x(t0)=x0

(4)

式中:x0是起始点的状态。轨道根数与终端状态之间的非线性关系表示为:

[af,ef,if,Ωf,ωf]T=ψ(r(tf),v(tf))

(5)

其中:tf为终端时刻，af,ef,if,Ωf,ωf分别是终端轨道半长轴、偏心率、倾角、升交点赤经、近地点幅角。轨道倾角和升交点经度可用地心惯性坐标系下位置与速度表示如式(7)所示，半长轴、偏心率和近地点幅角如式(9)～(11)所示。

hf=r×(tf)v(tf)=[hx,hy,hz]T,

(6)

cosif=hz/hf,tanΩf=-hx/hy

(7)

(8)

(9)

(10)

(11)

其中:r×(tf)为矢量r(tf)对应的叉乘矩阵，v×(tf)为矢量v(tf)对应的叉乘矩阵。

定义最低安全轨道高度为hsafe，终端质量m(tf)和高度r(tf)应满足：

m(tf)≥mf，r(tf)-R0≥hsafe

(12)

其中:mf表示剩余燃料耗尽后运载火箭与有效载荷的总质量，R0表示地球半径。

推力下降故障的救援类型可分为以下三种，如图1所示。①可飞入目标轨道。推力下降较小或推力故障的时刻较晚。②可飞入救援轨道。此时火箭的运载能力损失较大，不能将载荷送入目标轨道。通过在线救援轨道决策与飞行轨迹规划，可将载荷送入救援轨道。③运载能力下降非常大，火箭可达的轨道低于安全轨道，任务失败。安全轨道定义为以hsafe为轨道高度的圆轨道。文本研究的救援轨道的智能决策对应于第②种救援类型。

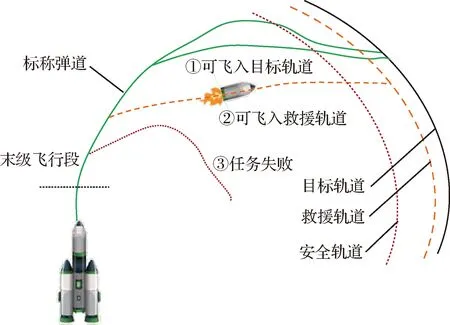
图1 推力下降情况下的轨迹重规划示意图Fig.1 Schematic diagram of the trajectory re-planning in the case of thrust drop

发生推力下降故障时，为避免坠落，提升轨道高度是首要目标。同等近地点高度下将载荷送入圆轨道所需能量小于椭圆轨道，因此在当前轨道面内搜寻最大高度圆轨道，将其作为最优救援轨道[9]。此时，推力故障下的轨迹重规划问题描述为半长轴最大(MTA: maximum terminal semi-major axis)优化问题：

(13)

可以看出，推力故障下的轨迹重规划问题(MTA)中的目标轨道是未定的，这将导致搜索空间显著增加，直接求解上述MTA优化问题存在计算效率低和不易收敛的困难。

2 最优救援轨道的决策模型

本文将推力故障下的轨迹重规划问题(MTA)转化为最优救援轨道的在线智能决策和成熟的燃料最优轨迹规划问题进行求解，以提高在线计算效率，如图2所示。在离线部分，遍历不同推力下降故障状态，基于动力学模型离线优化轨迹，建立“故障状态-救援轨道”样本集，以此为基础离线训练径向基神经网络，建立救援轨道决策模型。在线部分，将救援轨道决策模型迁移到在线应用，利用实际飞行的故障状态作为输入，在线决策出救援轨道。决策出的救援轨道作为终端约束，以此为基础构建燃料最优轨迹规划问题进行求解。

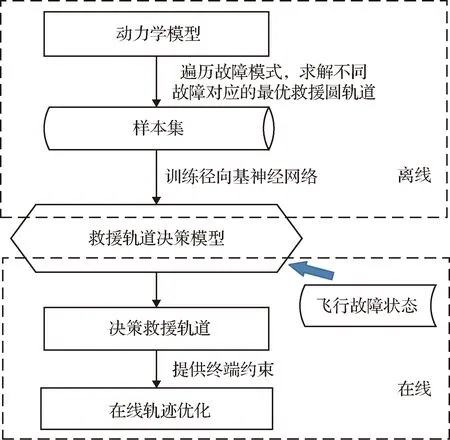
图2 救援轨道决策策略Fig.2 Rescue orbit decision-making strategy

2.1 救援轨道决策模型的离线建立

在离线部分，基于动力学模型通过遍历大量的故障情况建立运载火箭的“故障状态-救援轨道”样本集，在此基础上建立用于救援轨道决策的径向基神经网络模型。动力学模型中复杂的非线性关系用机器学习模型逼近，进而在线应用决策出救援轨道。利用机器学习模型的快速“输入-输出”能力，避免了基于动力学模型在线优化的繁重计算。

2.1.1样本集产生

发生故障前，如果运载火箭能准确跟踪标称弹道，那么推力下降的大小、发生推力故障的时刻足以描述所有故障模式。实际飞行中，由于存在噪声干扰，火箭的位置、速度、质量在标称弹道附近。因此，故障的特征是故障发生的时间、推力下降的大小、位置、速度、质量。

遍历不同故障状态，构建的MTA优化问题，采用自适应伪谱法[22-23]求解最优控制问题，如图3所示。为了保证知识库的丰富性，样本集的产生需遍历尽可能多的故障状态。求解得到的“故障模式-救援轨道”数据集，可作为径向基神经网络训练的样本集。

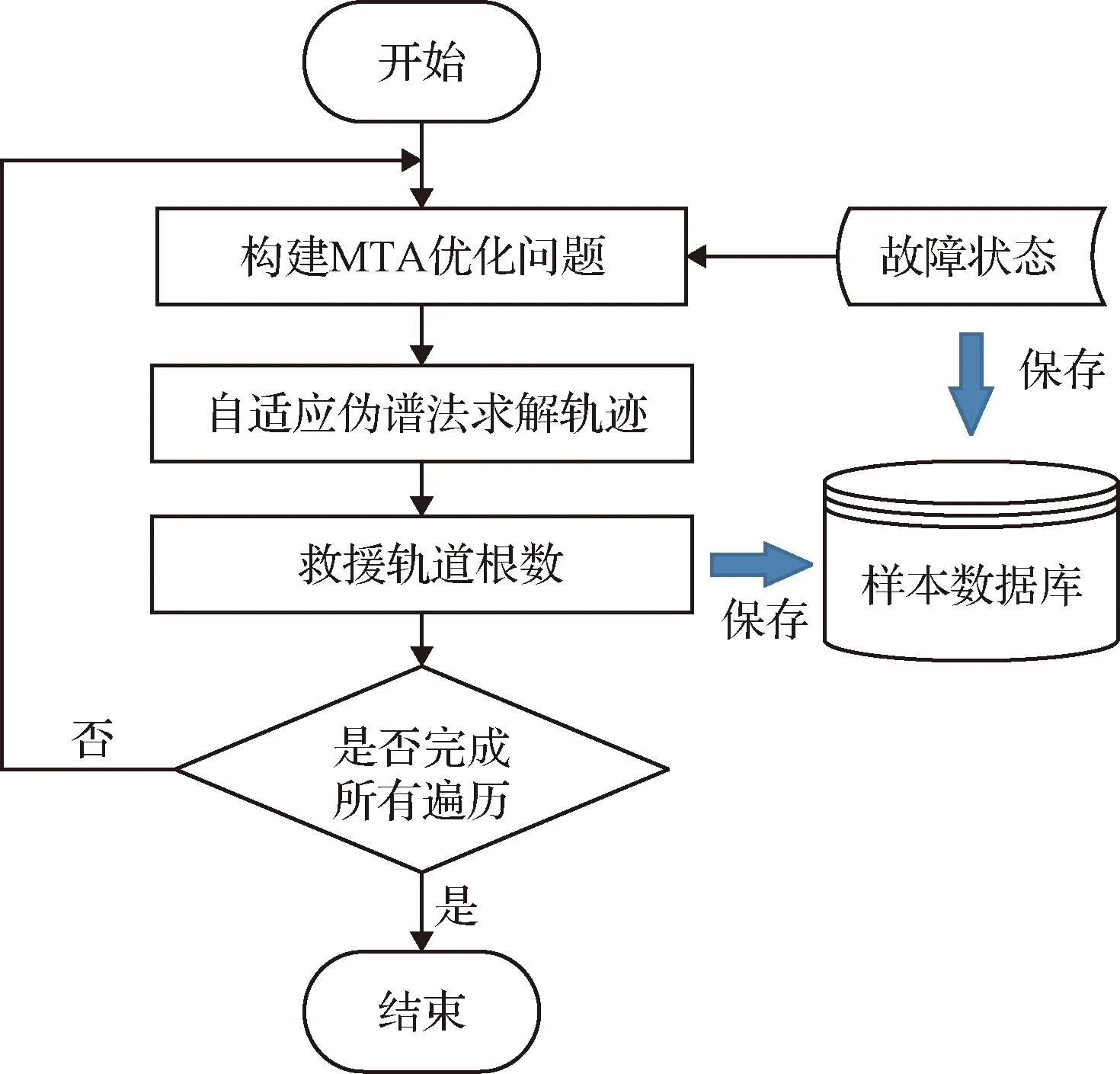
图3 样本集产生流程图Fig.3 Sample set generation flowchart

为了消除各维数据间数量级差别，避免因为输入、输出数据数量级差别较大而造成的预测误差较大，需要对数据做归一化处理。采用最大最小法对数据归一化，将所有数据规范化到[-1,1]之间。

2.1.2救援轨道决策模型建立与训练

径向基神经网络是一种局部逼近网络，通常由输入层、隐藏层、输出层三层网络构成，如图4所示。隐藏层有多个神经元，每个神经元由径向基函数构成，其基函数中心的维度取决于输入变量的维度。具有足够多隐层神经元的径向基神经网络能以任意精度逼近任意连续函数[24]。径向基神经网络的输入的特征包括推力故障的时刻、推力下降的大小、位置、速度和质量，输出的最优救援轨道根数包括轨道半长轴、倾角、升交点经度。

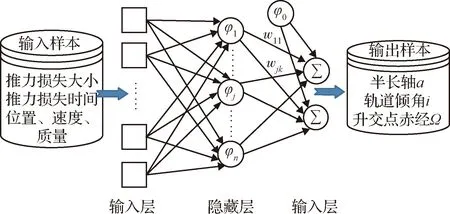
图4 径向基神经网络Fig.4 Radial basis function neural network

隐藏单元由基函数激活，本文采用高斯基函数，第j个隐藏层的输出为：

(14)

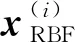
(15)

式中:wjk为第j个隐层神经元到第k输出神经元的权重。为了达到合适的逼近精度，通过训练来确定以下参数：隐藏层神经元的数量、每个隐藏层神经元基函数中心、径向基函数输出传递到求和层的权重。

正交最小二乘法(Orthogonal least squares,OLS)是由Chen等[25]提出的一种选择RBF网络数据中心的方法，训练的网络规模小，隐藏层采用少量的神经元节点就能映射非线性关系。OLS形式的径向基神经网络中神经元数量参数较少，神经元连接权重参数也少。因此迁移到在线应用的神经网络模型占用的存储空间较小，适合用于救援轨道决策。

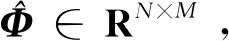
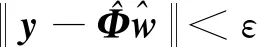
(16)

(17)

(18)

(19)

M个矢量的能量总贡献为:

(20)

若采用传统的直接法,最优救援轨道是基于动力学模型优化求解获得，而救援轨道决策模型把在线基于动力学模型优化的任务离线完成，分担了在线最优救援轨道决策的计算负荷。

3 基于救援轨道决策的在线轨迹重规划

本节提出的基于智能决策的在线轨迹优化过程如图5所示。当运载火箭飞行中出现推力下降时，故障监测系统可以测到推力下降的时刻和大小。将当前故障状态输入到箭上装订的离线训练好的救援轨道智能决策模型，可快速决策出救援圆轨道根数。决策出的轨道根数包括半长轴、轨道倾角和升交点赤经，作为在线轨迹规划的终端约束，通过求解对应的燃料最优(MFC:minimum fuel consumption)轨迹规划问题完成故障下的在线轨迹重规划。

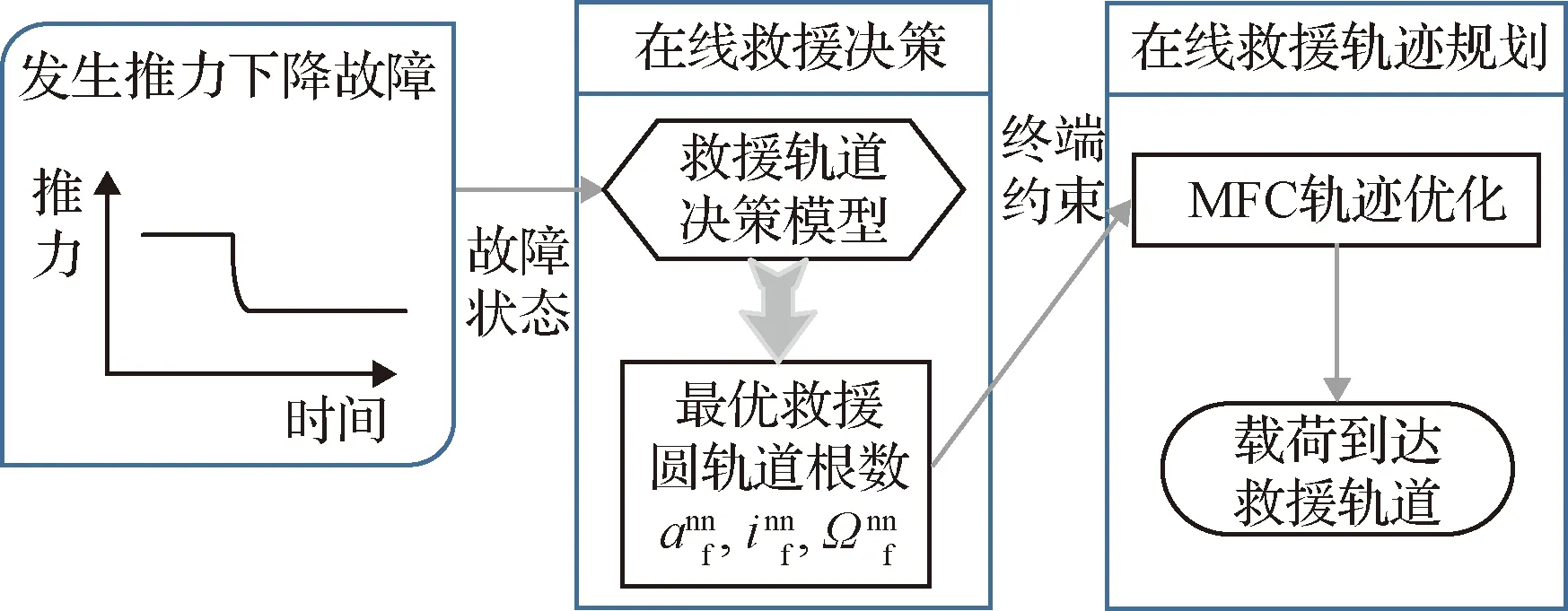
图5 基于智能决策的在线轨迹重规划Fig.5 Online trajectory replanning based on intelligent decision-making

由于圆轨道不存在近地点幅角的概念，轨迹优化问题的终端约束只有四个。基于动力学模型、约束在线构建燃料最少(MFC)优化问题：

(21)

采用径向基神经网络的救援轨道决策模型执行效率非常高，因此本节提出的基于智能决策的在线轨迹重规划方法的计算效率主要取决与燃料最优轨迹规划问题(MFC)的求解。MTA优化问题中的目标轨道是未定的，这将导致很难给定合理的初值，直接求解上述MTA优化问题存在计算效率低和不易收敛的困难。与MTA优化问题相比，MFC优化问题有许多成熟的轨迹设计方法，本文采用基于合理初值的自适应伪谱法在线求解。MFC优化问题的目标轨道根数是已知的，轨迹优化的初值较为合理，具有更好的收敛性和高效性，适合用于在线应用。

4 仿真校验

在本节中，以运载火箭的整个二级飞行阶段为研究对象，发射参数见表1。地球引力系数μ设为3.986×1014m3/s2，假设地球是一个均匀的球体，地球半径R0等于6378.14 km。第二阶段上升阶段为真空环境，其中Isp是发动机比冲，g0是海平面重力加速度，等于9.8 m/s2。

表1 发射参数Table 1 Launcher parameters

表2给出了发射惯性坐标系中的第二阶段初始状态。发射惯性系原点为发射点，X0轴指向火箭水平面内发射方向，Y0轴沿地心与发射点的连线方向指向天空，Z0轴满足右手定则。

目标轨道的近地点和远地点高度分别为200 km和300 km。目标轨道的轨道要素见表3。安全轨道高度hsafe=160 km。

表2 二级的初始状态Table 2 Initial states of second stage

本文的数值仿真都是在英特尔酷睿i7-7700 CPU 3.60 GHz电脑上进行的，MATLAB版本为2018b。

表3 目标轨道的轨道根数Table 3 Target orbital elements

4.1 救援轨道决策模型评估

依据2.1.1节样本集的建立方法，建立各故障状态的救援轨道根数的样本集。样本集建立的故障的状态分布按发生时间0～375 s，步长为1 s；推力下降大小13%～40%，步长为1%。除去可进入目标轨道和救援轨道高度低于160 km的故障状态，需要救援的故障状态如图6所示。图6所示的故障区间用传统的摄动制导、迭代制导无法将载荷送入目标轨道。

图6 训练集与测试集Fig.6 Training set and test set

推力下降的越大或推力发生的故障的时间越早，火箭运载能力的损失越大。在样本集中，随机抽取90%的数据作为训练集，剩余10%的数据作为测试集。采用径向基神经网络来建立故障状态到救援轨道的非线性映射。径向基神经网络训练的扩散因子是1，最终训练好的隐藏层神经元数量是50。测试集轨道根数误差的分布图如图7～图9所示。半长轴决策的绝对误差在[-0.25,1.25] km区间，相对误差在0.015%以内。轨道倾角、升交点赤经的绝对误差在10-4度以内，最大相对误差在10-5量级。

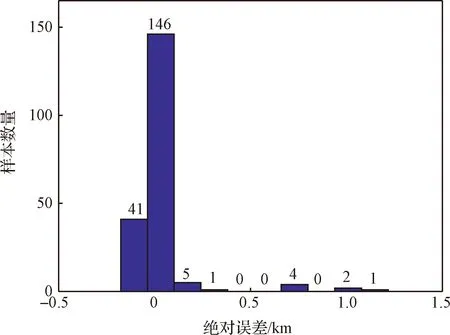
图7 半长轴决策误差分布Fig.7 Error distribution of semi-major axis decision

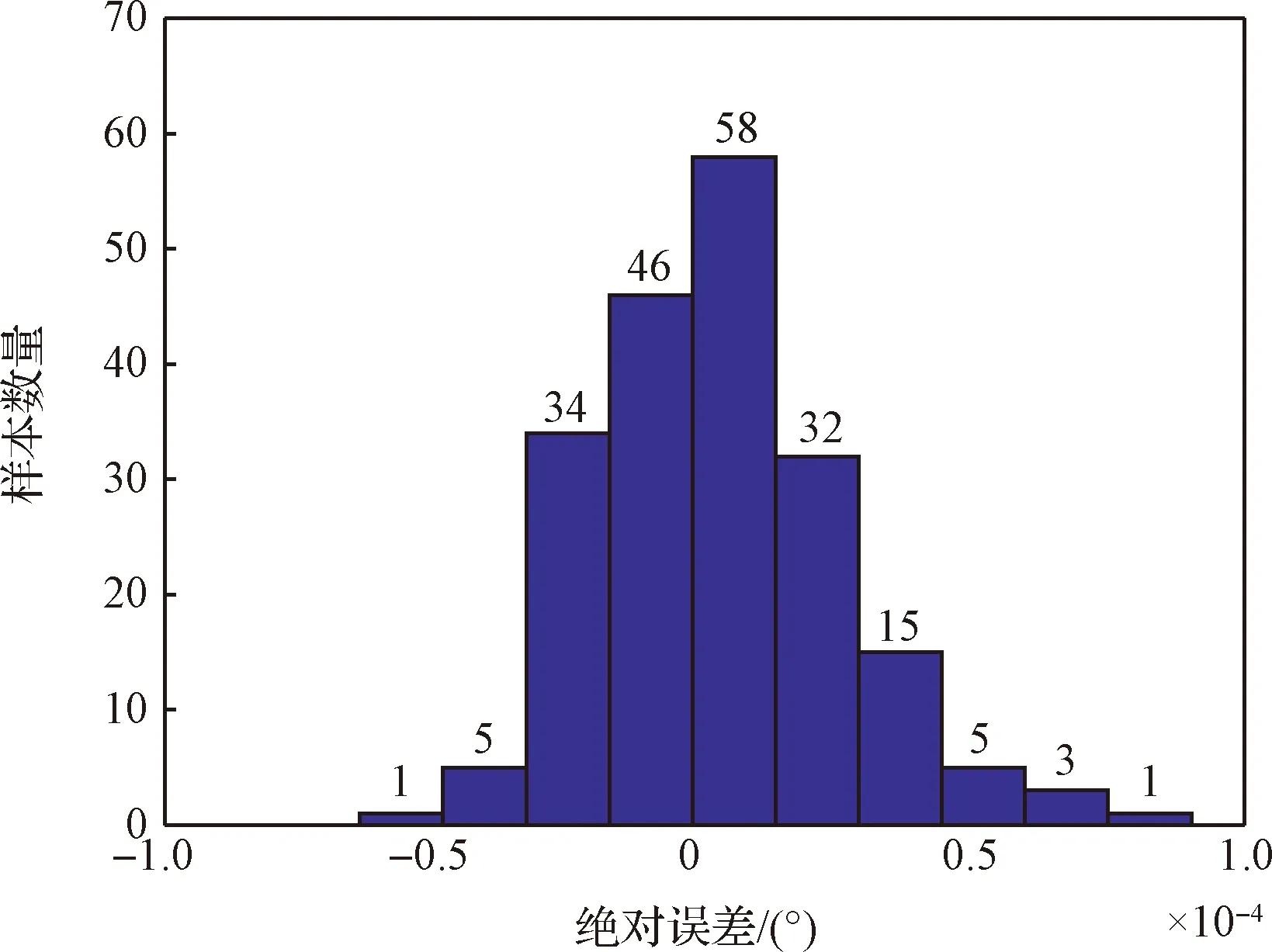
图8 轨道倾角决策误差分布Fig.8 Error distribution of inclination decision

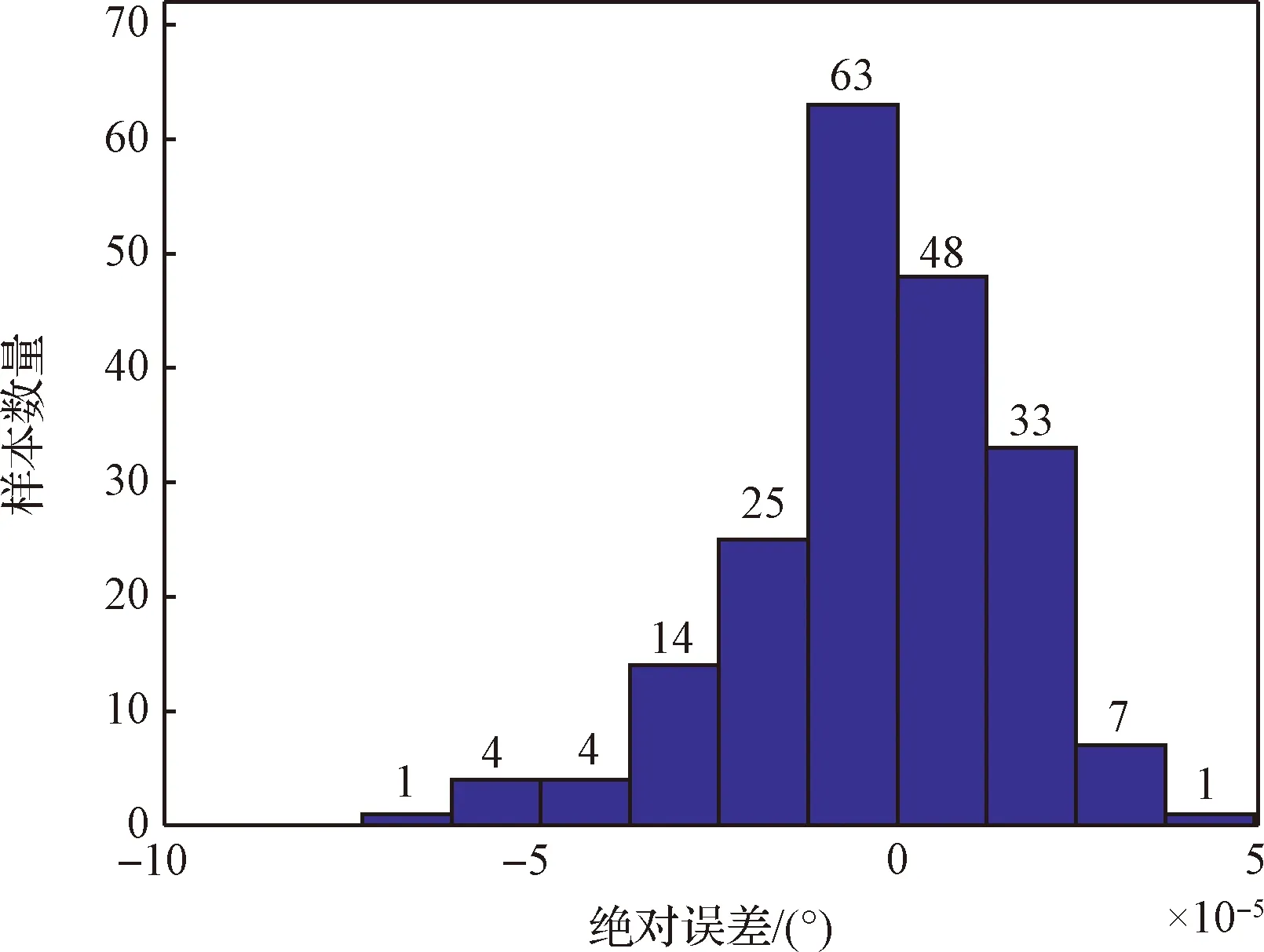
图9 升交点赤经决策误差分布Fig.9 Error distribution of longitude of the ascending node decision

采用均方根误差(Root mean square error,RMSE)来评估救援轨道半长轴决策的结果：

(22)

式中:N为测试集样本个数，yi样本集中半长轴，y′i为机器学习模型决策出的半长轴。

表4是不同机器学习模型的结果均方根误差的对比。线性回归得到的均方根误差比非线性回归方法的大，是因为故障状态与救援轨道根数是非线性关系，适合用非线性的函数逼近方法。与其他几种的机器模型相比，径向基神经网络模型的RMSE更小，意味着其在映射“故障状态-救援轨道”具有更好函数逼近的效果。

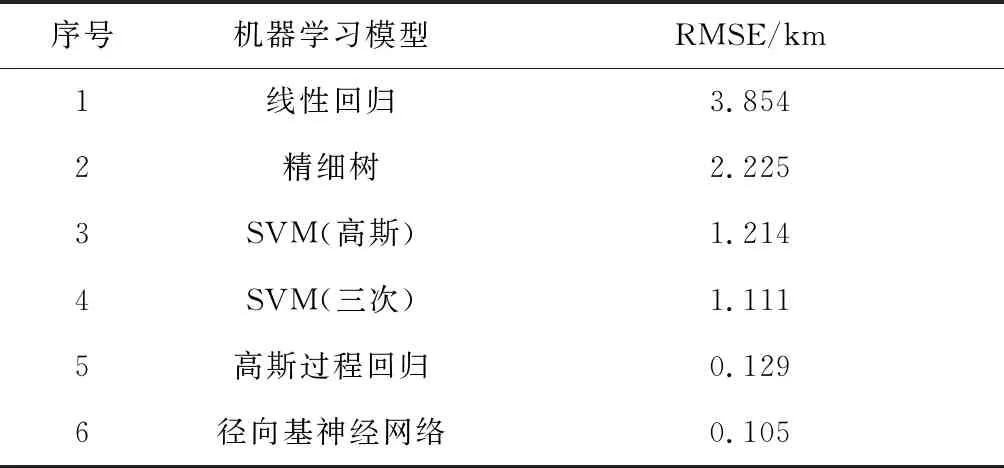
表4 不同机器学习模型的RMSETable 4 RMSE of different machine learning models

4.2 推力下降情况下在线轨迹优化

救援轨道决策需要将离线训练的径向基神经网络迁移到在线应用。以推力在104 s下降25%故障为例，分别采用直接求解MTA优化问题、本文提出的基于智能决策的在线轨迹重规划方法(RBFNN+MFC)去在线求解轨迹，其中MTA问题和MFC问题都采用自适应伪谱法求解，结果如图10～图13所示。自适应伪谱法所采用的配点是正交Legendre多项式的零点。对于104 s下降25%故障，直接求解MTA问题数值方法的最终离散点是209，RBFNN+MFC问题数值方法的最终离散点是41。两种在线轨迹优化方法都在104 s故障发生后调整了推力方向，延长飞行时间进入最优救援轨道。从图10、表5可以看出MTA方法和RBFNN+MFC方法的入轨海拔高度都是186.5 km，说明智能决策模型给出了与最优救援轨道一致的结果。从图13可以看出，标称的推进剂是富余711.4 kg，发生故障后，为了使救援轨道的高度最优，MTA和RBFNN+MFC方法的燃料全部用完。

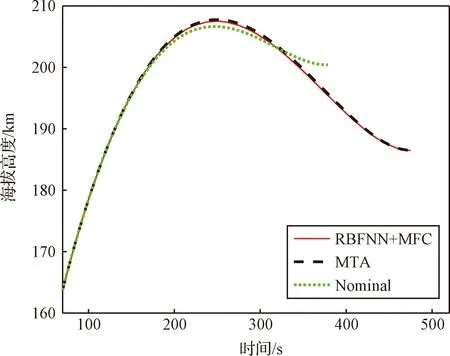
图10 海拔高度曲线Fig.10 Curve of altitude

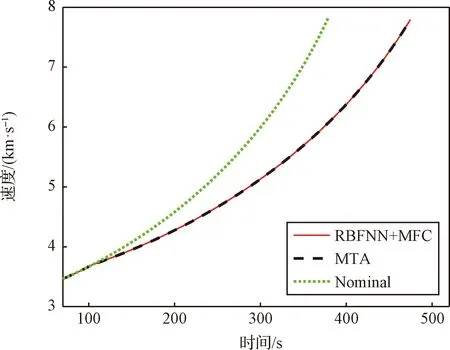
图11 速度曲线Fig.11 Curve of velocity

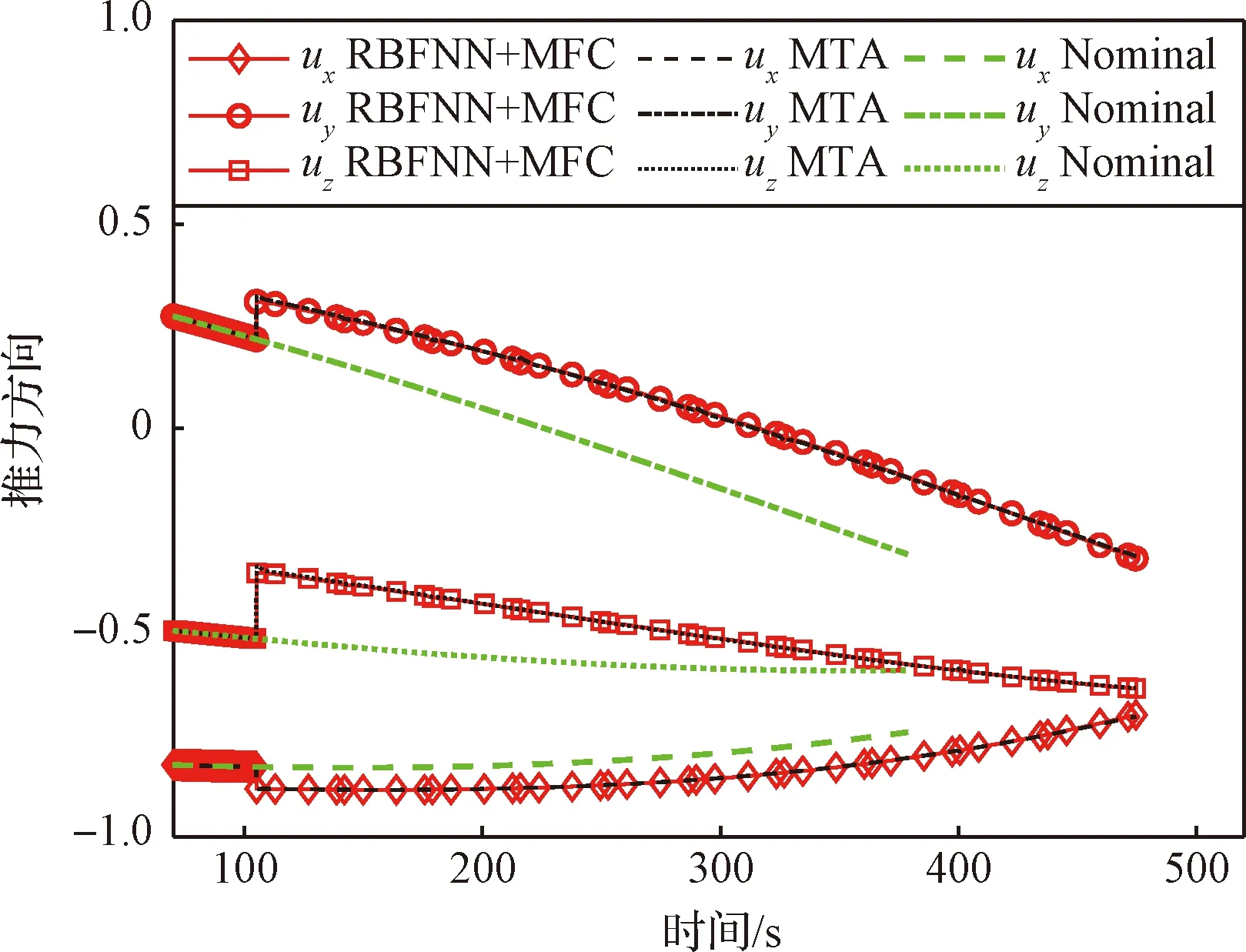
图12 发动机推力单位矢量分量Fig.12 Unit vector component of engine thrust

图13 推进剂质量曲线Fig.13 Curve of propellant mass

表6给出了MATALB环境下计算时间。对于在线轨迹重规划，直接求解MTA问题的计算时间是470 s，采用RBFNN+MFC方法的计算时间是0.7657 s，计算效率提高了两个数量级以上。同时在线救援轨道决策的计算时间在0.0057 s以内，相对于MFC问题的计算时间(0.76 s)几乎可以忽略，这与前面的分析是一致的。

表5 不同方法入轨的轨道根数Table 5 Orbital elements of injection point by different methods

表6 计算时间Table 6 Calculating time

5 结 论

针对运载火箭推力下降故障问题，本文引入机器学习方法，提出了一种基于智能决策的在线轨迹重规划方法，将原救援轨道未定的轨迹规划问题转化为最优救援轨道的在线智能决策和成熟的燃料最优轨迹规划问题进行求解，显著简化了在线轨迹重规划问题的求解。仿真结果显示本文提出的方法与直接求解原轨迹重规划问题相比，计算效率提高了两个数量级以上，同时给出一致的最优救援轨迹，非常有利于在线救援轨迹的重规划。

值得注意的是，如果救援轨道的半长轴决策结果是正误差，推进剂不能支持火箭到达半长轴正误差对应的轨道。因此在工程应用中，可适当降低半长轴决策结果作为燃料最优轨迹规划问题的终端约束，以保证轨迹的存在性。