流式鲁棒子模覆盖算法的图集覆盖问题的研究

田 歌，王耀力，常 青，孙永明

（1.太原理工大学信息与计算机学院，山西晋中 030600；2.山西省林业科学研究院，山西太原 030000）

数据汇总是机器学习中的一个主要挑战，它的任务是从大型数据集中找到可管理大小的代表性子集。包括图像摘要、文档和语料库摘要、推荐系统和非参数学习等许多应用程序。获得数据汇总的一般方法是：首先选择数据元素的子集，然后对所选集合的“代表性”进行量化，以构成优化效用函数。通常，用于汇总的效用函数表现出子模性，即自然递减的收益性质[1]。换句话说，子模性意味着随着摘要中包含更多数据点，数据集中任何元素的增加值都会减少收益。因此，可以将数据汇总问题自然地归结为子模覆盖问题[2]。数据汇总通常采用集中式算法，但集中式算法对于大型数据集来说不切实际。因为顺序选择单个机器上的元素在速度和内存方面受到很大的限制。因此，为了大规模地解决上述子模优化问题，需要利用MapReduce式的并行计算模型，或借助于流算法[3]。

而在实际应用当中，应用程序往往受限于数据存储容量与数据存取速度等因素，流算法往往是其可行的选择。流算法来源于大数据。自1987 年以来，世界人均存储信息的能力每40 个月翻一番。算法面临着存储、通信、分析等挑战。流算法仅需存储少量可用数据，而且内存大小可以远小于输入数据的大小。流算法不仅可以避免对内存的大量随机访问，而且可根据当前数据及时提供数据预测，从而促进实时数据分析[4]。

但在很多情况下，人们希望提取的代表集合是具有鲁棒性的。例如网络中的结点出现故障或者结点本身的变化，异或是当集合中的某些元素被移除时，希望集合还能保持其稳定性和代表性[5]。综上所述，文中对现有流式子模覆盖算法进行改进，同时加入鲁棒性判断，使其选出的代表性集合可以最多抵抗m元素的可能移除。

1 基于流算法的子模覆盖问题

1.1 传统贪婪子模覆盖算法

标准子模覆盖(SC)问题中，目标就是找到最小的子集S∈V使其满足特定的效用Q，即：

SC 问题是一个典型NP 问题，一种简单的贪婪策略是在每个阶段选择被覆盖元素最多的集合[6]。该算法的伪代码如下。集合C包含覆盖集合的指标，集合U存储X中未覆盖的元素。最初C为空，U←x，反复选择覆盖U元素最多的S集合，将其添加到覆盖项中。

贪婪集和覆盖算法的伪代码如下：

1.2 基于流算法的子模覆盖算法

引入流算法主要是解决子模覆盖问题，同时保持较小的内存并且不对数据流进行大量传递[7-9]。

2017 年，Baharan 等人提出解决大规模数据问题时可以将数据分发给几个机器，寻求并行的计算方法，或者使用流算法来扩大子模优化[10]。2009 年，Barna 等人首次将流算法应用到集覆盖问题的研究中，主要集中在半流模型上，其内存被限制为O(n)[11]。2014 年，Emek 等人证明，如果将流算法限制为仅对数据流执行一次传递，最佳的近似保证为[12]。2015 年，Chakrabarti 等人通过放宽单通道约束，设计了一个p-pass 半流(p+1)n1/(p+1)近似算法，并证明其本质上是严格的(p+1)3的因子[13]。2016 年，Ashkan等人提出了首个流式子模覆盖算法ESC-流算法，它仅需按任意顺序对数据进行一次传递，并提供任何ε>0，就可以得到最佳解决方案的2/ε的近似值，同时达到指定效用的1-ε，该算法仅需要O((klogk)/ε)的内存[14]。

定义1：对于任何数量的p通道和任何m大小的流，p通道流算法至少以的概率将子模数覆盖问题近似为小于的因子，必须使用大小至少为的内存。

用m表示数据流的大小。当p=1 时，任何近似比大于m/2 的单程流算法都必须至少使用Ω(m)的内存。ESC流算法采用两个阶段，第一个阶段允许内存大小的参数M作为输入。该算法保留t+1=logM/2+1 大小的代表集。每个代表集最大为2j，并且具有对应的阈值。一旦新元素e到达流中，它将被添加到所有未完全填充的代表性集合中，并且这些元素的边际增益高于相应的阈值，即该算法仅需要对数据流进行一次传递。该算法第一阶段对于流的每个元素的运行时间都是O(log logM),因为每个元素的计算成本是O(logM)次的oracle 调用[15-16]。

ESC 流式子模覆盖的伪代码如下：

step1：ESC 流算法-选择代表集

Step2：ESC 流算法-响应查询

已知值，执行以下步骤：

1：在S0,…,St上进行二分查找；

2：返回最小集合Si，使得f(s)≥(1-ε)Q；

3：如果不存在这样的集合，则返回“违反假设”。

2 改进的流式子模覆盖算法

2.1 算法流程

鉴于目前提取的代表集合中，当集合元素变化时或者某些元素增加删除时，无法保证集合的稳定性。为了使选出的代表集合能够具有抵抗部分元素被移除和替换的性能，对以上流式子模覆盖算法进行改进。

对于任何集合E⊆V，其中|E|≤m，存在一个最大为k的子集Z⊆SE，满足：

则认为对于参数m，集合S是鲁棒的。c是一个近似率。用OPT(k,VE)表示VE大小为k的最佳子集（即在删除E个元素后）。

基于以上定义，文中改进后的流式鲁棒子模覆盖算法(SRSC)的步骤如下，该算法也需要两个阶段:

阶段1：需要输入一个非递减的单调子模函数，基数约束为k、鲁棒性参数为m、阈值参数为t。对于部分α∈(0,1]，参数t是对于f(OPT(k,VE))的α近似值。因此，它依赖于f(OPT(k,VE))，但是f(OPT(k,VE))是未知的。因此在所提算法中假设f(OPT(k,VE))是已知的。该算法同ESC流算法一样，只需要对数据流进行一次传递，并输出一组最优元素。

阶段2：SRSC 接收在流传输阶段构造的集合S，去除元素E⊂S的集合，将基数约束k作为输入。然后返回最大为k的集合Z，该集合只需要在集合SE上运行上述简单贪婪算法即可获得。

文中所提算法为流式鲁棒子模覆盖算法(SRSC)。

流式鲁棒子模覆盖算法的伪代码如下：

step1：SRSC 算法-选择代表集

2.2 算法性能分析

2.2.1 下界

首先分析算法的下界，由于流算法可以被概念化为知道输入流不同段的玩家间的通信问题。因此，必要通信总量的下限产生流算法所需的内存量的下界。通信的下界意味着流的下界。

而合适的通信对复杂问题始于多玩家指针跳跃问题。

定义2：令T为深度l≥1 的完整t进制数（因此k=l+1 ≥2 层），则：

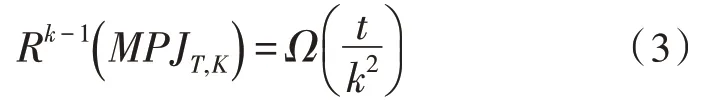
令MPJT,p+1为具有p+1 级别的完整t进制数T上的多玩家指针跳跃问题的实例，而π 为问题的输入，分布在p+1 个玩家P1,P2,…,Pp+1中。因此在m集合中，文中构造了SRSCt,p+1,l中的一个实例I()π，对于一些整数l≥t，有：

在文中的例子中k=p+1。

p-pass流算法ALG使用M大小的内存将SRSCt,p+1,l近似为小于的因数，其中，流由P1的集合和P2的集合组成，依此类推。文中使用ALG为MPJT,p+1设计一个[p,(p+1)M,1/3]协议PRTCL如下：

在i=1,…p的每个回合中，在ALG中模拟第i次传递；当ALG中处理流与P1对应最后一组集合时，将内存的内容广播到所有玩家。然后，在ALG完成流上的P2，依此类推直至Pp+1之后执行相同的操作。

由于ALG将I(π)的s*大小近似小于的一个因数，概率至少为2/3，因此PRTCL 输出MPJT,p+1概率至少为2/3。回想游戏MPJT,p+1是在p+1 个玩家中进行的，从定义2 中可以知道，M必须至少为

2.2.2 鲁棒性

对于流式鲁棒子模覆盖问题，文中让OPT(k,VE)代表选出子集的最优：

于SRSC 对数据集执行一次传递并且构造一个集合S，其大小最多是O((k+mlogk)logk)个元素。对于这样一个集合S和任意集合E∈V，满足 |E|≤m，则：

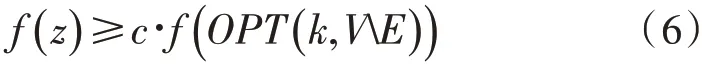
根据贪婪算法可以得到：

文中先从贪婪算法中得出：

再将式（7）带入得到：

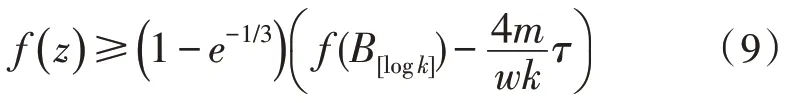
最终得到：

总结文中结论与过去的流式子模覆盖问题，给出了这些算法实现的近似因子、传递次数和空间界限。流式子模覆盖算法边界总结如表1 所示。

表1 流式子模覆盖算法边界总结

3 仿真实验与分析

3.1 实验概述

在很多应用中，例如社交网络中的影响最大化，图形中的社区检测等，重点的是从庞大的图形中选择小部分顶点，这些顶点在某种意义上“覆盖”了一个图的很大一部分。

为了评估SRSC 算法的可使用性。文中考虑了两个基本的集合覆盖问题：“支配集合”和“顶点覆盖”问题。并将其应用到网络图中3 个不同大小、不同类型的数据集中进行分析和比较。分别是由爬虫BUbiNG 得到的“eu-2015”，这是在2015 年底拍摄的一个大型的欧盟国家的快照。它由1 070 557 254个节点和91 792 261 600 条边组成。人类活动生成的有向社交网络“enwiki-2013”，是2013 年2 月底维基百科英文部分的快照。它由4 206 785个节点和101 355 853 条边组成。从公共来源抓取的“ego-Twitter”由来自Twitter 的“圈子”(或“列表”)组成。它由81 306 个节点和1 768 149 条边组成。以上3 种图都是稀疏的，因此需要较大的覆盖解决方案。将文中算法与随机选择和ESC 流算法进行比较。

3.2 支配集问题

给定具有顶点集V和边集E的图G(V,E)：ρ(S)表示图中S的顶点领域，δ(S)表示图中的边连接到S中的一个顶点。支配集即是选择覆盖顶点集V（即顶点集）的最小集的问题。其对应的效用函数为：f(s)=|ρ(S)∪S|，为单调子模函数。设置算法中M=520 MB,a=2，Q=0.7|V|。

在支配集问题中，从图1 中可以得出，文中SRSC算法与ESC 流算法的性能基本保持一致，甚至在数据集越大且顶点选择覆盖越多时性能略优于流算法。

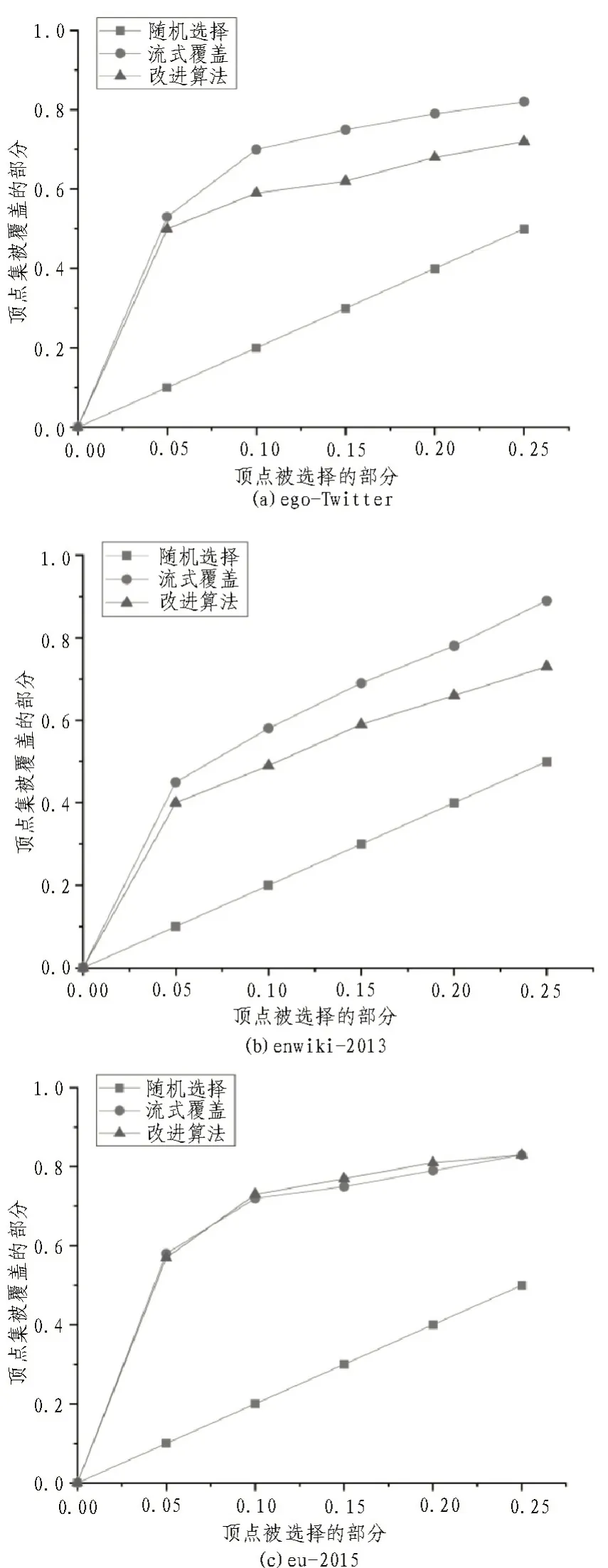
图1 不同算法下支配集问题情况

3.3 顶点覆盖问题

给定具有顶点集V和边集E的图G(V,E)：δ(S)表示图中的边连接到S中的一个顶点。顶点覆盖是选择覆盖边缘集E的最小集合问题。其对应的效用函数为：f(s)=|δ(S)|，为单调子模函数。

设置算法中M=320 MB,a=2,Q=0.8|E|。

在顶点覆盖问题中，从图2 中可以得出，文中算法却略差于ESC 流算法，但比起随机选择已经有了相当大的提升。

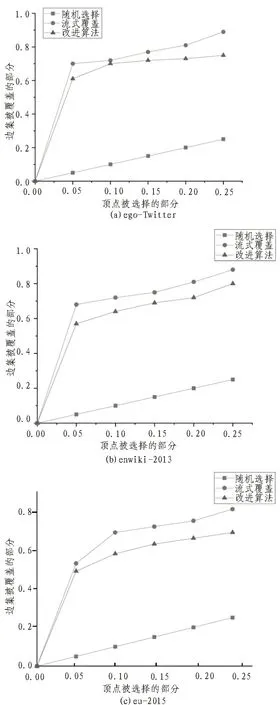
图2 不同算法下顶点覆盖情况

3.4 鲁棒性测试

文中算法不仅可以动态提取代表性的集合，也可以预先知道哪些元素将被删除，保证代表集合的稳定性，文中将选取上述数据集“ego-Twitter”，在支配集的问题中比较，删除不同k值时对集合覆盖的影响。

由图3 可知，在删除数据k值从100 至500 变化时，文中算法比ESC 流算法受到删除元素的影响少，其稳定性提高了10%以上。

图3 删除给定数据情况下两种算法支配集问题的表现

4 结论

文中讨论了流式子模覆盖问题的优化，对其集合加入鲁棒性判断，使其算法选出的代表集可以在部分元素被删除时还能具有其对应的稳定性和代表性。实验证明，在文中模型下采用流式鲁棒子模覆盖算法，相比其他流式算法，集合稳定性提高了10%以上，可以适用于更复杂的场景。