基于线性回归模型对北京市PM2.5含量的统计分析

廖锡欧

（首都师范大学 数学科学学院，北京100048）

PM2.5指环境空气中直径不大于2.5微米的颗粒物，它在空气中能悬浮较长时间。空气中PM2.5的含量越高，空气污染就越严重。与其他直径较大的大气颗粒物相比，PM2.5粒径小，面积大，活性强，容易附带有毒、有害物质（如重金属、微生物等），并且在大气中能停留较长的时间、输送距离较远，因此PM2.5对人体健康和大气环境质量的影响更大。研究发现，相比于PM10，PM2.5所携带的有害物质更多，且易被人体的呼吸道黏膜吸附于体内，引发一系列的呼吸道和肺部疾病。

对于PM2.5的研究，相关性分析、主成分分析、多元线性回归分析等都是主流的分析方法。宋红凤等对杭州地区的AQI项指标建立了多元回归线性模型，并对PM2.5和其他五项指标及其对应污染物含量之间的关系进行研究。李波等通过对长沙市的AQI指标进行相关性分析，并建立自回归移动平均模型对长沙市的PM2.5进行预测。丛琳等人建立了PM2.5与其余指标的线性回归模型，同时基于主成分分析进行改进，建立了更为精确的多元回归模型。

北京是我国的政治、文化中心，也是我国最早进入工业化的城市之一，随着工业化的发展，工业化污染不断加剧，环境遭受污染。进入21世纪以来，由空气污染造成的“雾霾”问题一直是众多学者讨论和研究的对象。为了研究PM2.5与其他指标的关系，本文采用主成分回归分析，找到影响北京市空气质量的关键因素，为日后相关研究和环境治理提供理论依据。

1 数据的收集和北京市空气质量的基本情况

本文所采用的数据全部来自中国空气质量在线分析平台，北京市2020年一年的AQI指数及AQI的六项指标，无缺失数据，故可以直接对数据进行建模。此外，将各变量换算成同一单位，以消除量纲对数据分析的影响。

对北京市空气质量评价进行汇总，从表1中空气质量良的累计频率可以看出2020年北京市大多数时间空气质量是良好的，轻度污染的频率为18.31%，中、重度污染的频率仅为3.01%和2.73%。这表明，近几年北京市的空气质量治理初显成效，但仍有中度污染和重度污染的时候，因此空气质量的改善和治理的工作仍需继续落实。

表1 2019年1月至2021年1月北京市空气质量情况

2 模型的建立

2.1 变量间的线性关系

选取2020年每日的AQI指数各项指标，通过R语言分别绘制出PM2.5与其他指标的散点图。

由图1不难看出PM2.5与其他变量之间存在较为明显的线性关系。而CO和NO2，PM10和CO之间存在较为明显的相关性，因此初步判断各自变量之间存在复共线性。为了验证这一猜测，我们考虑自变量PM10数据的列向量xi1，SO2数据的列向量xi2，CO数据的列向量xi3，NO2数据的列向量xi4，O3数据的列向量xi5，i=1，2，...，366组成的设计矩阵X。

图1 各变量之间的散点图

表2 各变量的相关性

2.2 主成分分析

通过收集2020年366天北京市AQI各项指标的数据，利用R语言对PM10、SO2、CO、NO2、O3进行主成分分析。从表3可以看出，前两个主成分的累计贡献率高达74.21%，超过了70%。说明前两个主成分很好地包含了原始数据的大部分信息，主成分分析良好。

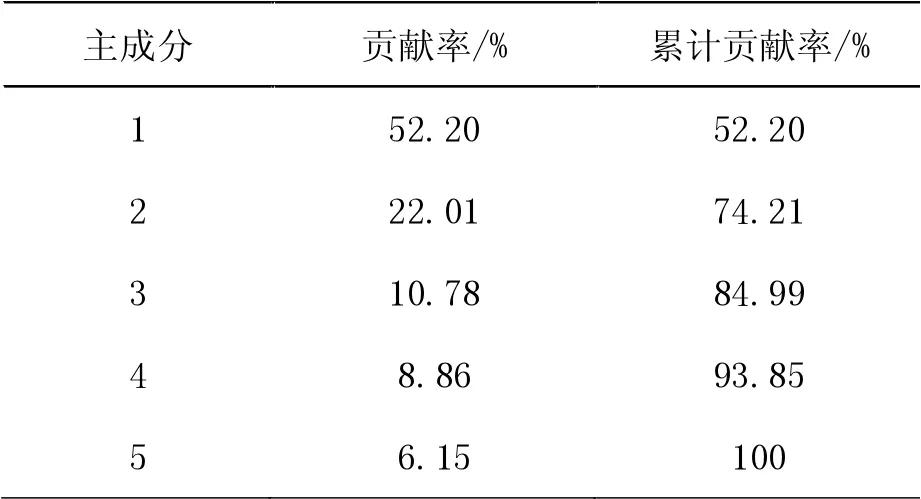
表3 主成分的累计贡献率

提取前两个主成分，表4是主成分载荷矩阵，呈现了前两个主成分在各变量上的载荷值。可以看出，第一个主成分（下记z1）在PM10、SO2、CO、NO2上的载荷较大；而第二主成分（下记z2）主要作用在O3上的载荷较大。因此，两个主成分是相互独立的，不存在复共线性问题，可进行回归分析。下面我们以PM2.5为因变量，两个主成分为自变量，通过主成分回归分析，探索因变量PM2.5与自变量PM10、SO2、CO、NO2、O3之间的相关关系。

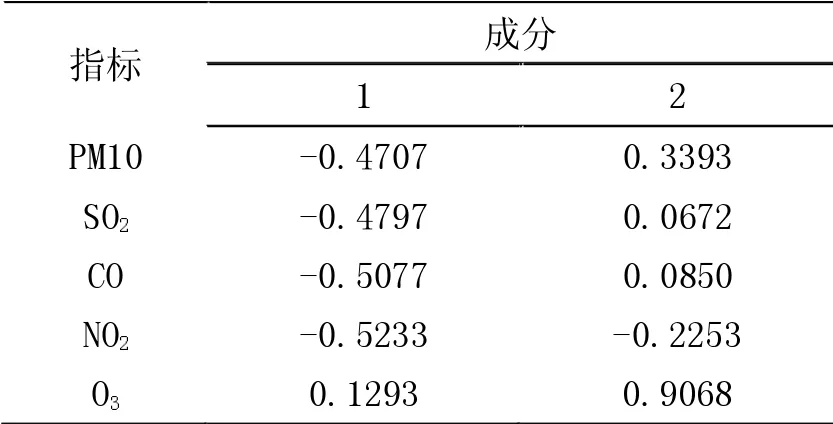
表4 主成分载荷矩阵

2.3 主成分回归分析

因为两个主成分不存在复共线性，再由图2可以看出，z1和z2无线性关系。PM2.5与z1之间存在明显的线性关系，PM2.5与z2主成分存在线性关系。并且PM2.5与第一主成分的相关度是极高的，因此对这两个主成分做多元线性回归是合理的。

图2 主成分散点图

用R语言对z1、z2做主成分回归，由表5可以看出，模型拟合度较高，解释了绝大部分的数据信息。并且通过了回归方程显著性的检验，因此对PM2.5和z1、z2建立回归模型是显著有效的。同时，主成分回归系数的检验说明两个主成分的回归系数均呈显著特征，即主成分与变量是显著相关的。于是，可以得到主成分的多元线性回归方程为：y=15.7853z1+6.5180z2+37.8525；其中，变量y代表的是PM2.5。

表5 主成分回归结果

由此可以看出，PM2.5与z1、z2都成正比。为进一步提高模型的精确程度，利用统计诊断找出异常点，并解释原因，接着用忽略异常值点之后的数据再生成主成分回归模型。

3 统计诊断

3.1 cook距离

考虑多元线性回归模型Y=Xβ+ε，E（ε）=0，Var（ε）=σ2In，定义cook距离为，i=1，...，n；这里

于是，对于每一组观测数据，可以用一个Di来刻画它对回归系数估计影响的大小。但直接计算Di会很不方便，因此引入Di的简便公式：

这里hii是帽子矩阵H=X（X′X）′X′的第i个对角元，ri是学生化残差。由此定义的cook距离衡量了第i组数据到试验中心的距离，显然，若cook距离越大，则该组数据离其他实验数据越远。若一组数据距离试验中心很远，并且对应的学生化残差又很大，那么它必定是强影响数据，这是一种基于描述性统计的异常值检验方法。

3.2 实例研究

利用R语言软件，分别计算出所有样本点的cook距离，制作散点图，在一定标准下计算出强影响点的范围，确定强影响点（见图3）。

图3 cook距离散点图

一般来说，如果一组数据点的cook距离大于4/（n-k-1）时，我们称它为异常值点。这里n为数据观测组数，k为自变量个数。由此得到强影响点集，发现北京市的强影响点主要集中在每年11月至次年的2月，而这段时间正好是北京的冬天，空气质量表现为轻度污染或中度污染，认为主要是由于冬季供暖烧煤、乘车出行尾气排放所导致。

4 模型优化

在删除强影响点之后，对剩下的数据进行主成分回归。从表6可以看出，在删除强影响点之后，拟合优度R2得到了提高，模型解释程度得到了优化。另外，考虑到删除一些数据后对模型主成分选择的影响，因此采用逐步回归的方法对zi进行筛选。经过逐步回归后，z1、z2仍得到保留，并且都通过了回归系数显著性检验，AIC值得到显著降低。因此，我们仍保留两个主成分，最终得到线性回归模型：

表6 修正后的主成分回归结果

其中，

5 结束语

本文通过收集2020年北京市的AQI及其六项指标，研究了导致北京市“雾霾”问题的主要因素PM2.5与其他观测指标之间的相关关系，在利用主成分回归分析消除了变量间复共线性影响之后建立了多元线性回归方程，并对方程进行了优化，最终得到了PM2.5与其他变量指标的线性回归方程。由回归方程可以看出，PM2.5与第一主成分的相关性较大，即与PM10、SO2、CO、NO2有较大的关系，而与O3的关系相对较弱。因此为了改善北京市的空气质量，必须先控制空气中尘土的含量，城市施工面积需要控制，而对于SO2、CO、NO2这类气体，则需要控制汽车尾气排放，减少私家车出行，多乘坐公共交通；在冬天供暖的时候，可以考虑用地热等新能源逐渐替代烧煤供暖。同时，政府还应加大绿化面积，开发新能源产品，从污染等源头治理污染问题。

表7 逐步回归后的结果