硅晶体生长温度梯度及生长速度的数值模型建立与分析

林光伟，王 珊，高俊伟，张西亚，高德东*

(1.青海大学机械工程学院，青海 西宁 810016； 2.阳光能源(青海)有限公司，青海 西宁 810000)

太阳能高新技术与半导体技术应用的不断发展，要求硅晶体具有更高的品质[1]，这是硅晶体生产过程中需要解决的重要问题。由于硅晶体的质量是依靠生产过程的工艺参数来决定[2]。因此，对硅晶体生长过程的生长参数进行建模输出，是提高晶体质量的方式之一[3]。

在硅晶体生长参数的研究中，前人主要从温度以及生长速度两个参数进行优化。这是因为温度的分布会影响晶体中点缺陷和原子氧的形成、扩散和聚集，同时会影响晶体冷却过程中产生的残余应力[4-5]。而均匀的晶体生长速度能让结晶过程稳定进行并提高晶体质量。因此,Natsume等[6]研究了硅晶体生长速率与温度梯度的关系，建立了晶体生长过程的体积辐射传热模型，采用体辐射算法对参与的不规则壳体进行辐射分析，达到了预测晶体生长炉内的温度分布的目的。Winkler等[7-8]提出了一种基于模型的晶体生长过程控制的新方法，该方法将非线性模型的控制器作为控制系统的核心并与传统的PID控制器相结合使用，实现了对晶体直径和生长速率轨迹的跟踪。此外，还实现了从称重信号重建晶体半径和晶体生长速率。Neubert等[9-10]使用复杂的非线性模型和传统线性PID控制器的组合来跟踪晶体半径和生长速率，并且以加热功率和提拉速度作为操纵变量，实现控制作用。Abdollahi等[11]建立了晶体生长和半径生长的几何模型，并设计线性化的控制器来调节和跟踪所需的参考晶体半径，为晶体生长和温度调节的复杂耦合系统提供了一个统一的调节框架。刘兵[12]在对热场的控制系统进行研究时，分析了生长晶体的热传递示意图，以及晶体的热传导方程，以此导出了晶体中温度矢量沿轴向和径向的分量。段伟峰等[13]在对硅单晶等径阶段直径模型辨识与控制研究中，分析了在固液界面处能量的流动传递情况，建立了晶体直径、晶体提拉速度以及热场温度三者之间的关系，最终得到了晶体直径的表达方程。周耐根等[14]从分子动力学的角度出发，分析了晶体的生长速率与温度的关系式，研究了硅晶体生长速率与过冷度的关系，得出在晶体生长时，过冷度越大，晶体的生长速率越快。

但是考虑到在硅晶体生长过程中有固液气相混合热传递、熔体流动、固液界面的热力学现象和提拉生长过程的动力学存在，使得硅晶体生长研究在数值求解上依旧具有一定的复杂性[15]。最近有学者在晶体生长过程自动化的研究中[16]，建立降阶模型作为数值模型监测和控制的基础，以达到输出生长参数的目的。因此，基于简化的数值模型对求解晶体生长内部参数有重要作用，本文建立的非线性化数值模型将加热器的热量作为主要输入，将硅晶体生长速度及内部温度梯度作为目标对象进行输出，以实现对晶体生长过程的分析，从而提高晶体的最终质量。

1 数值模型建立

1.1晶体生长过程的动力学分析在硅晶体的生长过程中，最常用的方法是直拉法。在籽晶棒的牵引下，晶体被缓慢拉出熔体的同时在固液界面处发生凝固，由于机械装置的持续提拉，晶体获得不断的生长。要建立数值模型对晶体生长过程进行研究，需要分析晶体生长工艺过程，并处理重要的物性参数，最终实现对晶体生长过程中的温度分布及晶体生长速度的输出。考虑到硅晶体等径生长过程，即晶体直径稳定的生长阶段，各工艺参数与生长参数相对稳定，因此以下数值模型的分析与建立以等径生长阶段为主。图1为硅晶体生长过程的简化模型，多晶硅原料在坩埚中受到加热器的辐射加热，温度升高熔化形成硅熔体，种晶之后在晶体生长界面处凝固结晶形成硅晶体。同时，晶体与坩埚在不同方向具有一定的旋转速度，以保证晶体生长的稳定进行。图1中，Ml为熔体质量，Md为弯月面质量，Ms为晶体的质量。因此，在初始200 kg的投料量下，从硅熔体凝固结晶为最终的晶体，忽略结晶过程的少量损失，整个生长过程始终处于质量守恒状态。考虑到晶体的质量与晶体的生长速度有紧密关系，因此深入到硅晶体生长的微观界面(图2)，把晶体作为单独分析对象，晶体在生长过程中，在竖直方向上受到向上的提拉力F和浮力Ff，向下有晶体下表面受到的表面张力Fm和自身的重力G，进一步在力的矢量方向中进行表示。而晶体的生长速度vS受提拉速度vp、硅熔体液面下降速度vl、结晶速度vd及坩埚上升速度vc的共同影响，在速度矢量方向中表示。

图1 硅晶体生长二维简化模型Fig.1 Two-dimensional simplified model of silicon crystal growth

图2 硅晶体生长微观界面Fig.2 Micro interface of silicon crystal growth

根据动力学原理，在竖直方向上建立方程式为：

(1)

式中：Fm′为晶体下表面受到的张力在竖直方向上的分力，有Fm′=Fmcos(aC+aO)，aC与aO分别为倾斜角和晶体生长角。在晶体生长过程中，自身的重力不断增大，与重力呈线性关系的浮力与表面张力也随之增大，因此假定在竖直方向上的重力、浮力及表面张力互相抵消，可以得到：

(2)

随着结晶生长过程的不断发生，为保证生长界面始终处于同一水平位置，需要上升坩埚位置来弥补坩埚内熔体液面的下降，因此锅升速度vc方向向上。由于凝固结晶的速度vd及提拉速度vp的方向都为向上，坩埚内硅熔体液面下降速度vl向下。则，晶体生长速度vS表示为：

vS=vp+vl-vd-vC

(3)

在硅晶体的等径生长阶段，外部提拉速度保持恒定，提拉速度与坩埚的上升速度为常数，且有工艺参数埚跟比，即vp/vc=K为定值。

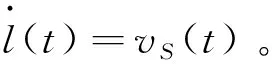
(4)

式中：ρS为晶体密度；晶体的半径为r；提拉力F(t)和晶体生长速度vS(t)都与时间相关。通过晶体生长的动力学过程分析，实现了外部提拉力与晶体生长速度的动态过程建立。

1.2晶体生长过程的热量流动分析进一步为找到温度分布与生长速度的关系，需要引入热量的传递，耦合动力学以实现对晶体生长速度及温度梯度的输出。由于数值模型的建立是基于等径生长过程，此过程热场处于热平衡，温度场处于稳定态，因此以加热器的输出热量流经晶体生长界面，到达晶体内部的流动过程进行分析。根据图3所示的硅晶体生长过程的热量流图，热量传递以热辐射和热传导为主。加热器的热量辐射到坩埚，坩埚通过热对流及热传导加热硅熔体，硅熔体温度升高在生长界面处凝固结晶形成硅晶体。

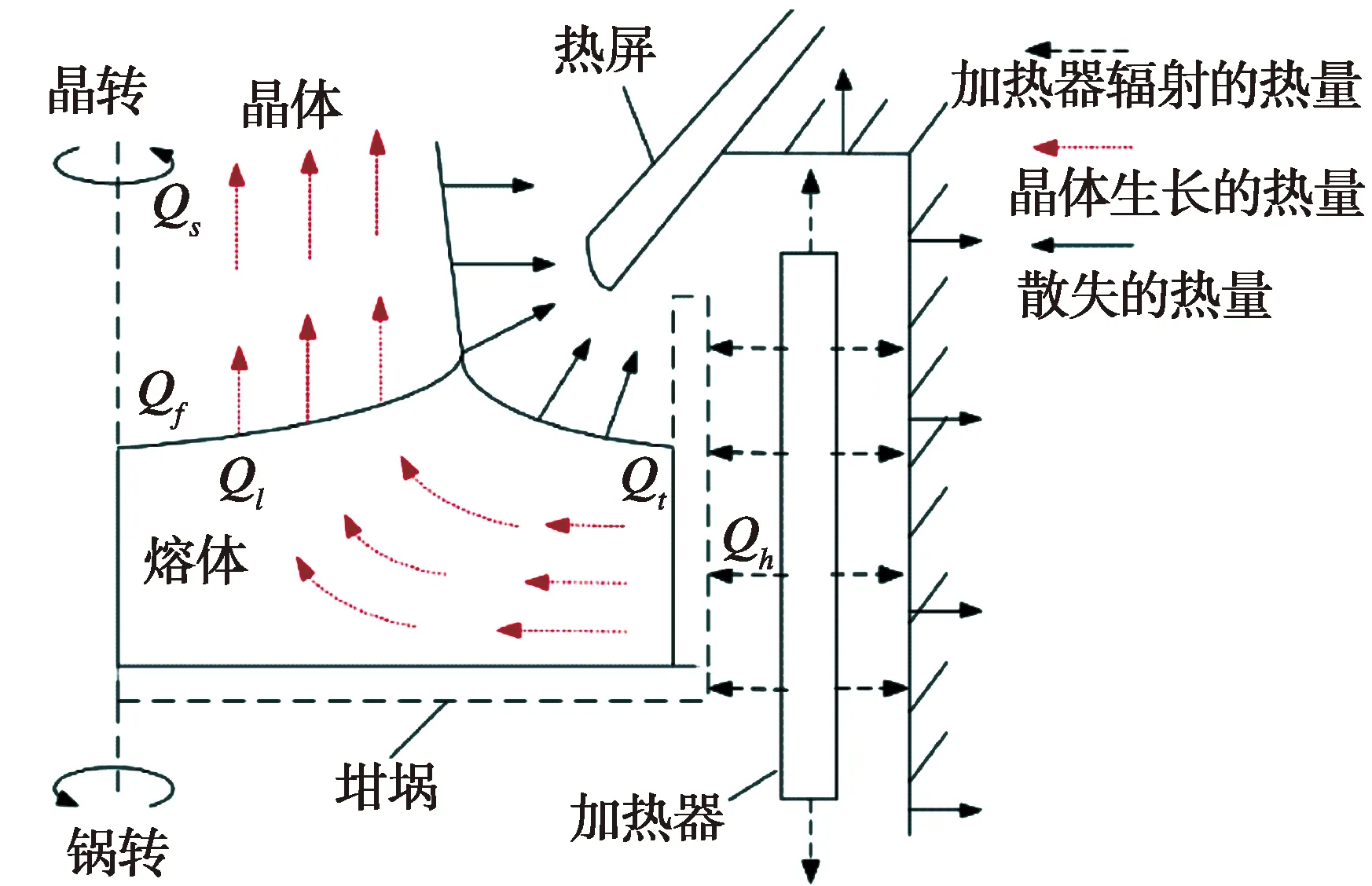
图3 硅晶体生长过程的热量流图Fig.3 Heat flow diagram of silicon crystal growth

依据上述分析，建立热平衡方程式。

加热器辐射到坩埚的热量Qt计算[17]如下：

Qt=Aσε(T12-T22)=k1Qh

(5)

式中：A为辐射到坩埚外壁面积；σ为Stefan-Boltzmann常量；ε为石墨加热器发射率；T1为加热器表面温度；T2为坩埚所处的环境温度；Qh为加热器输出热量，与加热器的功率相关。

加热器辐射于坩埚外壁的热量通过热对流及热传导传递到熔体，而到达熔体的热量，一部分会通过熔体的自由表面耗散，则到达生长界面的热量Ql=k2Qt。考虑到熔体内部的热对流过程及其复杂，采用此公式可以不用分析复杂的对流换热过程，通过熔体自由表面的温度计算出耗散的热量，计算出到达生长界面处的剩余热量。

由于晶体凝固结晶时会释放结晶潜热Qf，其中Qf=ρSπr2vdΔH，因此，到达晶体内部的热量QS为：

QS=Qf+Ql=Qf+k1k2Qh

(6)

联立式(3)与式(6)，则：

QS-kQh=ρSπr2ΔH((1-K)vp+vl-vS)

(7)

式中：k=k1k2为定值常数，ΔH为潜热。根据式(7)，建立了晶体生长过程的热量输入与晶体生长速度的关系。因此，将热量作为模型的输入，可以实现对晶体生长速度的输出。但为了对晶体生长的温度梯度进行输出，在式(7)基础上，还需进一步建立与晶体的内部温度梯度的联系。根据稳态温度场中晶体内的热传导方程，得到晶体内部的温度梯度沿轴向分量为[18]：

(8)

式中：h为晶体与环境的热交换系数与晶体本身的热传导系数的比值，为定值常数；x表示晶体在半径方向的距离。因此，式(8)可以求解出在半径方向上任意位置的温度梯度，但考虑到实际晶体生长过程中，红外温度测量仪器对晶体表面的温度测量比较准确，为后续更好的比较模型与实际晶体生长的温度差异，因此以x=r处作为模型的温度输出点，输出晶体表面温度梯度为：

(9)

1.3硅晶体生长的温度梯度及生长速度数值模型式(4)和式(9)分别建立了提拉力与晶体生长速度、加热器热量与晶体的生长速度及晶体温度梯度的关系。因此，将加热器的热量及外部提拉力作为模型输入，晶体的温度梯度及生长速度作为输出，建立数值模型，实现非线性化的输入输出。

考虑到外部提拉力是根据晶体的质量增大而均匀增大，因此在设置外部提拉力F(t)时，采用的方式是将实际生长过程中提拉力数值拟合成线性函数，再作为模型输入。而对Qh(t)输入采取的是对加热器的功率转化成热量再输入。

在式(4)的基础上，可以得到：

(10)

在式(9)的基础上，可以得到：

(11)

模型建立是在等径生长过程的封闭边界条件下，此时外部提拉保持恒速，晶体的生长半径为均匀半径，埚跟比固定，熔体高度均匀下降。因此，依据数值模型，在输入外部提拉力及加热器热量的情况下，可以实现对晶体的温度梯度及生长速度的输出。

2 数值仿真与计算参数

为验证模型的准确性，采用FLUENT软件对上述的数值模型进行仿真。仿真以CL120-97炉的二维炉体几何结构为基础，主要部件为热屏、单晶硅、石英坩埚、熔体硅、加热器、保温炭毡、锅帮等，物性参数如表1。将炉体进行四边形网格划分，网格总计37 152个(图4)。

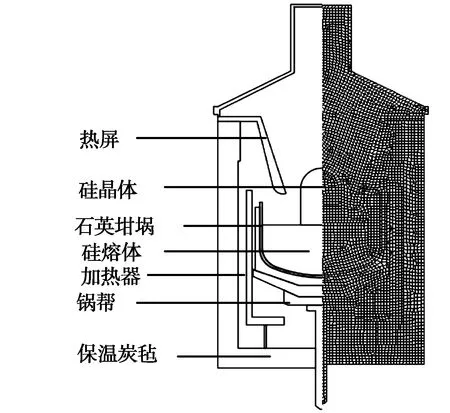
图4 单晶炉网格化Fig.4 Gridding of single crystal furnace

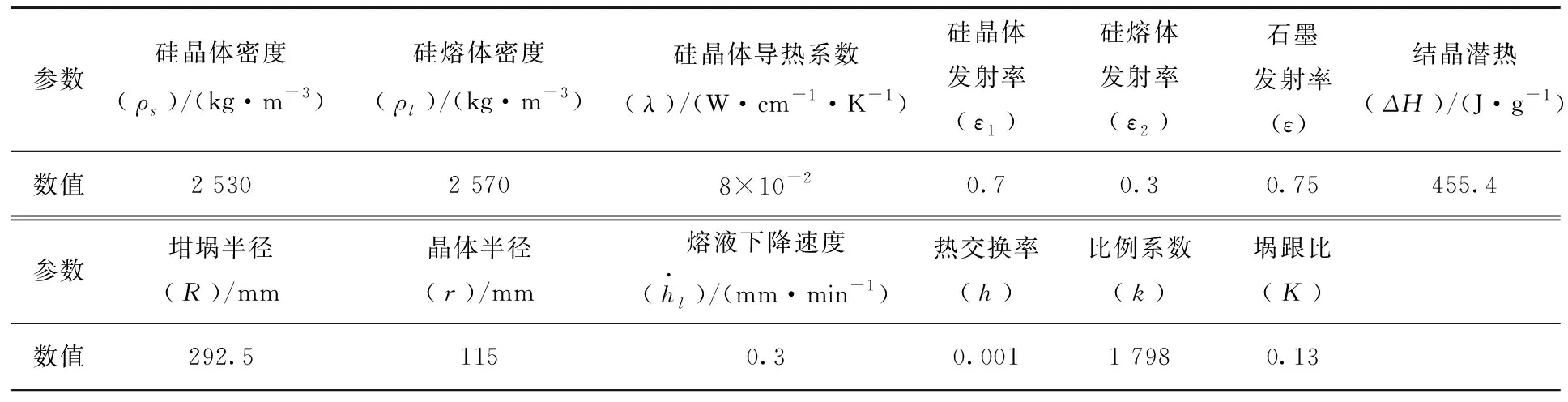
表1 晶体生长参数

由于数值模型只建立于晶体生长的等径阶段，该阶段中的单晶炉加热器功率输入恒定，晶体稳定生长。因此在模拟仿真时，保持单次实验的输入功率稳定，并且为了更加直观的比较输入功率对输出参数的影响，设置加热器输入功率为37.5～40.5 kW。为进一步验证数值模型极限条件，增加32.5 kW与50.5 kW作为输入功率。

提拉力的大小与晶体的重量相关，随着晶体质量的增大而不断增大。因此，根据阳光能源(青海)有限公司所提供的提拉力数据，将晶体生长过程中提拉力拟合成线性函数F(t)=1.286t+1.68(图5)，并将u1(t)=F(t)设置为晶体内部函数。

图5 提拉力拟合函数Fig.5 Fitting function of lifting force

加热器对熔体的加热满足热辐射方程，熔体与晶体内部传热满足热对流及热传导方程，模拟仿真中，热对流采用层流模型，速度的解耦合采用SIMPLE算法，扩散项的离散采用中心差分格式，对流项差分采用三阶QUICK格式。计算条件：坩埚内径为533 mm，炉内压力为2 600 Pa，氩气流量为50 L/min，生长界面处的温度为1 685 K，模型中的物性参数见表1，其他材料的参数在软件中添加。模型仿真以晶体生长的等径阶段为基础，在不同的输入功率下，研究分析晶体内部温度数值及生长速度的变化。

3 结果与分析

3.1 温度梯度结果对比

为达到仿真结果与实际实验结果的一致性，采用阳光能源(青海)有限公司CL120-97单晶炉(图6)，进行相同环境的晶体生长实验。在实际晶体生长中，采用高温红外测温仪对晶体表面的温度进行测量，测温仪的温度测量为500 ℃到2 000 ℃，精度较好。对晶体的生长速度的采集，先是通过布置在提拉杆上的速度传感器得到提拉速度，然后在经验公式的基础上利用计算机计算出晶体生长速度，最终通过显示器显示。在FLUENT软件中，将晶体的温度梯度数据输出，仿真结果如表2，图7a和图7b为模型仿真结果与实际结果的对比。为了对比验证数值模型的准确性，将模型所得到的温度数据与实际温度数据进行分析。

图6 实验用CL120-97单晶炉Fig.6 CL120-97 single crystal furnace for experiment

表2 不同加热功率下硅晶体表面温度数据

表2(续)

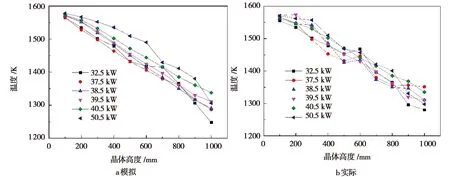
图7 等径生长过程中的温度Fig.7 Temperature during equal diameter growth

考虑到晶体生长过程中，温度梯度分布越均匀，晶体生长方向上温度线性化程度越高，所生长出的晶体质量越好。因此，采用线性度方程δ=1-Δy/y×100%，进一步拟合模型与实际生长的温度梯度线性程度。根据图7a，温度与拟合直线最大偏差为Δy1=53 Κ，温度y1=226 Κ，计算出δ1=76.5%；图7b，温度与拟合直线最大偏差为Δy2=34 Κ，温度y2=218 Κ，计算出δ2=84.4%。因此，得到数值模型与实际晶体生长的温度线性化程度相差W2=δ2-δ1=7.9%。

以上通过温度梯度误差及温度线性化程度分析，发现模型与实际晶体生长得到的温度数据误差为6.83%，线性化程度相差7.9%。在忽略外界干扰对于晶体温度的影响下，通过该数值模型所得到的温度接近于实际数据，能够反馈于模型输入，进一步通过调整数值模型的输入，即调整功率及提拉力，实现调节晶体的温度分布。

3.2 生长速度结果对比

通过FLUENT软件的仿真模拟，将晶体的移动速度作为晶体的生长速度输出，仿真结果见表3。为避免功率对晶体生长速度产生的影响，在仿真和实际晶体生长前半段时间，输入功率保持为39.5kW，结果对比如图8a和图8b，将模型得到的生长速度与实际生长速度进行分析。

表3 不同加热功率下硅晶体的生长速度

图8 等径生长过程中功率与晶体生长速度的关系Fig.8 Relationship between power and crystal growth rate during equal diameter growth

生长速度的线性化程度越高，则速度的波动越小，晶体生长越稳定。因此，同样采用线性度方程δ=1-Δy/y×100%，分析模型与实际生长速度的线性程度。图8a和图8b为不同输入功率下晶体的生长速度情况，对比速度波动最大时，两者的线性化程度，因此选取输入功率为32.5 kW时进行计算线性化程度。根据图8a生长速度与拟合直线最大偏差为Δy3=0.046 mm/min，速度波动y3=0.24 mm/min，计算出δ3=80.8%。根据图8b生长速度与拟合直线最大偏差为Δy4=0.084 mm/min，速度波动y4=0.3 mm/min，计算出δ4=72%。得到数值模型与实际晶体生长速度的线性化程度相差W4=δ3-δ4=8.8%。

通过生长速度的误差以及线性化程度分析，模型所得到的生长速度与实际晶体生长误差为1.67%，线性化程度差异为8.8%，表明该模型所得到的输出结果与实际晶体生长速度相当接近，能够作为理论分析的基础。同时，实际晶体生长的线性化程度低于80%，而模型得到的线性化程度为80.8%，这是因为在实际的晶体生长过程中，会受到氩气流动和熔体液面波动等因素的影响，导致晶体生长速度不稳定，所以进一步可以得出，数值模型所得到的数据相对实际晶体生长避免了环境因素的影响，更接近理想晶体生长速度，对反馈指导实际晶体生长过程更有意义。

4 讨论与结论

本文考虑到硅晶体生长过程中晶体的温度梯度以及生长速度对晶体最终质量的影响，因此建立数值模型输出两个参数，并在不同的加热器功率下，将模型结果与实际晶体生长过程对比。与Abdollahi等[11]建立的数值模型不同，该模型通过调整加热器功率、外部提拉力来弥补外部干扰对晶体生长产生的影响，优化了晶体生长环境。同时，该数值模型与Natsume等[6]研究的硅晶体生长速率与温度梯度模型相比，能更为简洁的得出硅晶体轴向温度的分布，达到预测晶体生长过程中温度梯度的作用。因此，与以往研究的晶体生长模型相比，该模型简化复杂的热质运输，考虑用于晶体生长的热量及外部体力动力，实现晶体生长过程的建模，同时该模型可以调节硅晶体生长过程中的热量输入，减少在晶体生长过程中所受到的干扰影响，保证晶体生长过程中处于稳定的生长速度及均匀的温度环境，对晶体生长数值模型的优化求解具有重要作用。

最终通过数值模型所输出的晶体温度梯度与实际晶体生长温度梯度的数据误差为6.83%，温度梯度的线性化程度相差为7.9%。所输出的晶体生长速度数据与实际数据的误差为1.67%，线性化程度相差8.8%，在未考虑外界干扰对于温度产生的影响下，模型所得到的温度数据接近实际晶体生长数据，速度波动范围小，数值模型得到的线性化程度好。表明该数值模型具有良好的一致性和实际性，可以输出接近实际生长过程中的温度梯度及生长速度，进一步实现指导晶体的生长。

因此，本文所建立的硅晶体生长温度梯度及生长速度的数值模型，实现了非线性化的输入输出，同时输出的结果接近实际的数据。在该模型的基础上，可以调节晶体生长速度的稳定与内部温度分布的均匀，减少晶体生长过程中所受到的干扰，提高晶体的最终质量。