冗余驱动的三平动并联机构性能分析与优化

叶 伟 胡利焕 夏董新 周哲佳

(1.浙江理工大学机电产品可靠性分析与测试国家地方联合工程研究中心, 杭州 310018;2.浙江理工大学机械与自动控制学院, 杭州 310018)

0 引言

三平动并联机构可以作为分拣装置应用到自动化打包生产线上，也可以串联转动关节形成五轴加工装备[1]，具有很好的应用前景。这类机构一般由3条分支连接动平台和基座构成，最典型的是Delta并联机器人[2]，适合应用于高速分拣领域。在构型设计方面，HUANG等[3]采用基于螺旋理论的约束综合法设计了一类具有对称分支的三平动并联机构。LI等[4]采用位移流形方法综合了一类具有良好结构刚度的三平动并联机构。杨廷力等[5]基于单开链单元，对三平动并联机构进行了构型综合。史巧硕等[6]采用GF集方法综合了一系列三平动并联机构。孟庆梅等[7]对一种三平动并联机构Delta-CU进行了误差建模，提高了机器人精度。ZENG等[8-9]对一种三平动并联机构Tri-pyramid进行了设计与分析。

作为少自由度并联机构中的一类，大多三平动并联机构存在运动耦合问题，导致机构分析困难、控制不便[10]。针对这个问题，学者们通过构型的巧妙设计，构造了具有运动解耦[11]或者部分解耦[12-15]的三平动并联机构。为了控制并联机构的运动，一般需要选取和自由度数目相等的驱动数。然而，为了消除内部奇异[16]、优化驱动力[17]、提高精度[18]等，设计者们经常在机构中安排比自由度数目更多的驱动数，使得机构具有冗余驱动的特点，获得更好的操作性能。在运行过程中，所有驱动协调地运动，共同控制机构的运动。QU等[19]提出了一种冗余驱动的4-RUU并联机构，相比于非冗余3-RUU机构有更好的操作性能。李仕华等[20]提出了一种冗余驱动三平动并联机构的综合方法，可消除机构的内部奇异。目前，同时具有运动解耦和冗余驱动两种特征的三平动并联机构实用构型鲜见报道。

本文提出一种运动部分解耦的冗余驱动三平动并联机构新构型，采用李群理论和修正的Grübler-Kutzbach(G-K)公式分析其自由度，并开展运动学、动力学分析与性能优化设计，以期为其工程应用提供理论依据。

1 机构描述与自由度分析

如图1所示，本文提出的并联机构由动平台通过4条分支连接机架组成。其中，分支1、2都是PRRR链(P为移动副，R为转动副)，分支3、4都是PRPR链。分支1和分支3共用与基座相连的P副，最后一个R副是以复合铰链的形式连接到动平台，并且，基座相连的P副与分支中R副轴线平行，另一个P副轴线垂直于R副。分支2、4结构类似。机构中与基座相连的两个P副轴线垂直且共面。

记分支1、3中各R副中心依次为A1、B1、C1、D1，分支2、4中各R副中心依次为A2、B2、C2、D2。连杆AiBi记为连杆1，其长度为l1，连杆BiCi记为连杆2，其长度为l2。动平台为边长2a的正方形。记过点A1、A2且方向平行于R副转轴的两直线交点为点o，在该点建立固定坐标系oxyz，x轴沿oA1方向，y轴沿oA2方向，z轴由右手法则决定。在动平台中心建立动坐标系puvw，点p为动平台中心点，u轴平行分支1中R副轴线方向，v轴平行于分支2中R副轴线方向，w轴由右手法则决定。点Di(i=1,2)与oxy平面的距离记为e1，D1与ozx平面的距离以及D2与oyz平面的距离记为e2。

采用李群理论[21]对机构的输出运动进行分析。考虑到分支1和分支3共用基座移动副，将分支1、3整体考虑，其到动平台的运动可表示为

L13={T(x)}({R(A1,x)}{R(B1,x)}{R(C1,x)}∩
{R(D1,x)}{T(rD1C1)}{R(C1,x)})={T(x)}{G(x)}

(1)

式中L13——分支1和分支3整体到动平台的运动集

{T(x)}——沿x轴方向的移动运动群

{R(A1,x)}——轴线过点A1且平行于向量x的转动运动群

rD1C1——D1C1方向的单位向量

{T(rD1C1)}——沿D1C1方向的移动运动群

{G(x)}——垂直于向量x的平面运动群

其余符号类同。

同理，分支2和分支4到动平台的整体运动集L24可表示为

L24={T(y)}{G(y)}

(2)

动平台运动集{M}为各分支运动集的交集，可得

{M}=L13∩L24=
{T(x)}{G(x)}∩{T(y)}{G(y)}=
{T(x)}{T(y)}{T(z)}{G(x)}∩
{T(y)}{T(x)}{T(z)}{G(y)}=
{T}{G(x)}∩{T}{G(y)}={T}

(3)

式(3)表明，该并联机构的动平台能输出空间内3个方向的移动运动。

采用修正的G-K公式[22]对机构的自由度进行计算，计算式为

(4)

式中F——机构自由度d——机构阶数

n——包括机架的构件数目

g——运动副数目

fi——第i个运动副的自由度

v——冗余约束数

本机构中，d=6，n=12，g=14，fi=1。分支1、3共用与基座相连的P副，除去该P副后，分支1内的RRR链与分支3内的RPR链都是位于同一平面的运动链，产生了3个冗余约束。同理，分支2、4内也产生3个冗余约束。对并联机构进行整体考虑，分支1、3的组合对动平台的约束是垂直于分支内转动副的2个约束力偶，同样分支2、4的组合对动平台的约束也是2个力偶，这4个力偶并不完全独立，仅限制了动平台的3个转动自由度，因此有1个是冗余约束。综上，机构中总的冗余约束数v=3+3+1=7。

将上述结果代入式(4)，可得

F=6×(12-14-1)+14+7=3

(5)

采用另一种思路，考虑机构构型特点，可认为杆A1B1、B1C1、A2B2、B2C2是产生虚约束的运动链，将其移除不影响机构自由度。移除虚约束部分后机构d=6，n=8，g=8，fi=1，冗余约束数v=1，代入式(4)，计算结果仍然是F=3。

根据李群理论和修正后G-K公式分析结果可知，本机构具有3个自由度，动平台能输出3个方向的移动运动。

为了控制本机构的运动，至少需要选取3个运动副作为驱动。考虑到机构中共有4个移动副，且都靠近基座，可都选取作为驱动，使机构具有冗余驱动的特点。在机构的运动过程中，可根据动平台的轨迹要求，通过运动学和动力学逆解求取4个驱动的输入参数，用于协调控制，使机构执行预期的运动。

该并联机构可应用于五轴机床或分拣机器人的开发。图2为五轴打磨机床实例，通过在动平台上安装一个AC摆头，打磨头与工件间形成五自由度相对运动，可实现任意曲面的五轴打磨。该机床是由4条分支共同支撑动平台，具有良好的结构刚度。

2 运动学分析

2.1 位置分析

位置分析是为了建立动平台输出参数和主动关节输入参数之间的关系。其中位置反解是已知动平台位姿，求解驱动关节输入量。本机构中，动平台的位置可由动坐标系原点p在定坐标系中的位置向量p=(x,y,z)T表示，4个移动副为机构的主动关节，移动副位移用di(i=1,2,3,4)表示。根据机构的参数，可得定坐标系中各点坐标为

(6)

根据机构的几何关系，求得其位置逆解为

(7)

对式(7)作变换，可以得到机构的位置正解为

(8)

式中“±”与机构装配方式有关，对应图2中装配方式应取“+”号。

根据式(7)、(8)可知，动平台在x方向的位移完全取决于d1，在y方向的位移完全取决于d2，在z方向的位移可由d2和d3(或d1和d4)决定，因此具有运动部分解耦的特点，在分析、轨迹规划和控制方面具有优势。

2.2 奇异分析

当机构处于或接近奇异位形时，会导致刚度下降、运动失控等后果，应对其展开分析。对位置方程求导，得到机构的速度方程，整理成矩阵形式为

(9)

其中

可以得到机构雅可比矩阵为

(10)

根据雅可比矩阵情况，并联机构的奇异位形可分为3类：逆解奇异、正解奇异和混合奇异[23]。

当只有det(JA)=0时，机构发生逆解奇异，此时动平台自由度瞬时减少。根据式(9)，该奇异在d3或d4为0时发生。由于实际机构中移动副行程限制，该类奇异不会发生。

冗余驱动并联机构在矩阵JB降秩时发生正解奇异。当z=-e1，即点D1、D2和p共面时，矩阵JB的第3列全为0，此时动平台沿z轴方向的移动运动不可控。图3为对应的正解奇异位形。

当逆解奇异和正解奇异的条件同时满足时，机构处于混合奇异位形。由于逆解奇异不会发生，机构也不存在混合奇异。

2.3 工作空间

由于各分支共同约束，并联机构的工作空间通常较小。给定机构参数a=50 mm，e1=23 mm，e2=40 mm，l1=50 mm，l2=200 mm。限定驱动1、2的行程范围为50～400 mm，驱动3、4的行程范围为175～350 mm。为避免杆件干涉，令BiCi和CiDi(i=1,2)的夹角大于45°。为避免奇异位形，令z>0，利用搜索法可绘制机构的三维工作空间如图4所示。可以发现，机构在x、y方向的移动范围为50～356 mm，在z方向移动范围为0～310 mm，具有较大的工作空间(图4)。

3 动力学分析

3.1 速度分析

动力学建模与分析是并联机构高速高精度控制的基础，采用螺旋理论结合虚功原理的方法[24]进行动力学建模。

在定坐标系中，令ria、rib、ric和rid(i=1,2)分别为点Ai、Bi、Ci和Di的位置矢量，分支1、2中PRRR链的运动螺旋可表示为

(11)

(12)

式中$ij——分支i中第j个关节的运动螺旋，i=1,2,j=1,2,3,4

O——零向量

分支3和分支4中PRPR链的运动螺旋表示为

(13)

(14)

本文并联机构只有3个移动自由度，因此动平台的速度与加速度可表示为

(15)

根据螺旋理论，动平台速度螺旋Vp在定坐标系中可以由分支中各关节运动螺旋的线性组合表示为

Vp=ωi1$i1+ωi2$i2+ωi3$i3+ωi4$i4

(16)

式中ωij——分支i中第j个关节的速度，i、j=1,2,3,4

式(16)可表示成矩阵形式

(17)

其中

式中Ji——6×4雅可比矩阵

由式(17)可求得分支i中各个关节的速度为

(18)

锁定分支中的驱动关节，可以得到一个约束螺旋$Ti与除驱动关节螺旋外的所有被动关节螺旋都互易，即$Ti∘$ij=0。该约束螺旋即驱动关节对应的传递力螺旋，各分支传递力螺旋表示为

(19)

式中$Ti——分支i的传递力螺旋，i=1,2,3,4

(20)

其中

式中Js——4×6雅可比矩阵

Δ——6×6算子矩阵

将式(17)代入式(20)中作变换后，可以得到并联机构各被动关节的速度与4个驱动关节速度之间的关系为

(21)

其中

式中Gi——分支i的一阶影响系数矩阵

分支i中第j个关节的速度螺旋Vij可以由驱动关节速度的线性组合表示为

(22)

注意到上述速度螺旋的参考点都为定坐标系原点o，当选择的参考点由点o转换到机构各部件质心处时，速度螺旋可进行变换，即

(23)

rij,C——原点o到分支i中第j个部件质心处的位置向量

S($)——螺旋原部

S0($)——螺旋对偶部

3.2 加速度与受力分析

类似于速度分析，动平台相对于定坐标系的加速度AP也可用分支各关节运动螺旋组合[25]表示为

(24)

其中

由式(24)可求得分支i中各关节螺旋加速度为

(25)

进一步可以求得机构各部件相对于定坐标系原点o的加速度螺旋为

(26)

式中Aij——分支i中第j个部件相对于点o的加速度螺旋与速度螺旋类似，分支i中第j个部件相对于其质心处的加速度螺旋Aij,C可表示为

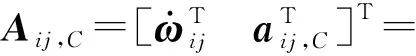
(27)

在求得各部件速度及加速度后，分支i中第j个部件质心处受到的惯性力/力矩螺旋FI,ij,C、重力螺旋FG,ij,C、外力/力矩螺旋FE,ij,C可分别表示为

(28)

式中Iij——分支i中第j个部件相对于定坐标系的惯性矩阵

mij——分支i中第j个部件的质量

g——重力加速度

fE.ij.C——分支i中第j个部件质心处所受外力

τE.ij.C——分支i中第j个部件质心处所受外力矩

机构分支i中第j个部件质心处所受的合力Fij,C可表示为

Fij,C=FI,ij,C+FG,ij,C+FE,ij,C

(29)

3.3 驱动力优化

根据式(9)、(10)，机构的驱动速度与动平台速度螺旋间的映射关系可表示为

(30)

其中

式中Jd——驱动速度与动平台速度间的雅可比矩阵

根据已求得并联机构各部件的受力与速度，机构运动时总体瞬时功率可表示为

(31)

其中

式中τ——驱动力

引入虚速度δVp，将式(30)代入式(31)可得

δP=FvJdδVp+τTJdδVp

(32)

在虚功原理中，虚速度δVp为任意值，为使得并联机构的总虚功δP始终为零，须满足

FvJd+τTJd=0

(33)

对于冗余驱动并联机构，其驱动关节数大于机构自由度，因此其逆动力学所求的驱动力组合并不唯一，存在无穷多种组合。不合理的驱动力组合可能导致机构部件之间的内力过大而对机构造成损坏，式(33)中雅可比矩阵Jd不为方阵，对其转置求伪逆后可得驱动力的最小二范数组合[26]为

(34)

3.4 数值仿真验证

通过ADAMS动力学仿真软件来验证上述动力学模型的正确性。机构各部件参数如表1所示。设定动平台做螺旋上升运动，其具体轨迹(单位：mm)为

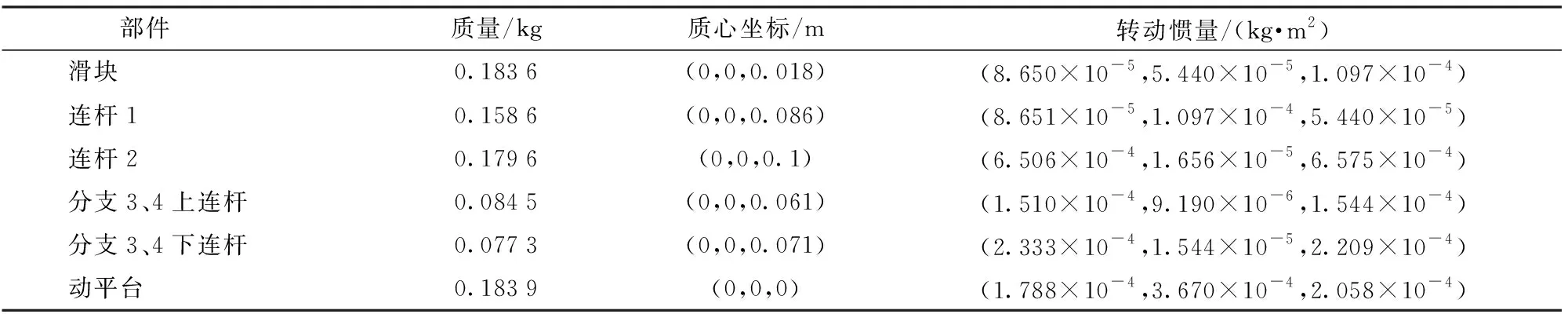
表1 并联机器人参数Tab.1 Parameters of parallel robot

(35)

式中tm——运动的持续时间，取0～5 s

在冗余驱动并联机构的仿真过程中，为解决逆动力学解不唯一的问题，将分支1～3的驱动关节位移量以及通过驱动力优化计算出的分支4的驱动力理论值输至ADAMS软件，这样动平台不仅能输出给定轨迹还能测量出唯一的驱动力组合。

图5为理论计算结果和仿真结果的对比情况，其中，驱动力曲线表示的是沿移动副移动方向驱动合力的幅值。可以看出基于螺旋理论以及最小二范数优化得到的驱动力和ADAMS仿真中的驱动力基本一致，最大偏差仅为0.6%。结果证明了并联机构动力学模型的正确性，可用于后续的动力学性能评估和控制系统设计。

4 性能评价

对于并联机构，可采用雅可比矩阵条件数的倒数对其运动学性能进行评价，即机构灵巧度指标[27]。灵巧度越接近1，表示机构运动学性能越好，而越接近0表明机构越接近奇异位形。雅可比矩阵J的奇异值为

(36)

式中λi——矩阵JTJ的特征值

灵巧度指标可表示为

(37)

为了解机构工作空间内运动学性能情况，取中间位置z=175 mm处的平面，绘制灵巧度指标分布如图6所示。可以看到灵巧度具有对称性，且与机构结构特点相符。

灵巧度指标反映了并联机构在不同位置下的运动学性能，为了评估机构在工作空间内的全域运动学性能，将κ1≥0.6的区域定义为优质灵巧度空间，定义优质灵巧度空间与整体工作空间的比值为全域运动学指标，即

(38)

式中W——机构的整体工作空间

SGT——优质灵巧度空间面积

S——整体工作空间面积

σ——全域运动学指标

σ的取值范围为0～1，其值越大表明工作空间内机构的整体运动学性能越好。

在动力学性能评估方面，动态可操作度椭球(Dynamic manipulability ellipsoid, DME)[28]是常用指标，该指标衡量了动平台在特定驱动力作用下改变位姿的能力。当驱动力被约束后动平台在不同方向上加速度范围的椭球[29]可表示为

(39)

(40)

同样，以z=175 mm处的二维平面为例，绘制工作空间内的DME指标分布如图7所示，可以看到动力学指标也呈对称分布，与机构结构特征吻合。

5 尺度优化

上述全域运动学指标可用于并联机构的尺度优化设计。以l1、l2和a为设计参数，采用空间模型法[30]来开展尺度优化。令标准化因子

(41)

无量纲参数与约束条件分别为

(42)

(43)

根据式(43)的约束条件，可以得到如图8所示的参数设计空间。无量纲参数与设计空间参数之间的关系为

(44)

通过计算可以得到全域运动学指标在参数设计空间中的性能分布如图9所示，定义图谱中σ=1的区域为性能优良区域。为了获得良好的运动学性能，可以选取性能优良区域中的参数作为机构参数，如s=0.6，t=2.6，可得优化后机构尺度参数为a=88 mm，l1=146 mm，l2=204 mm。同样取高度z=175 mm处的平面，绘制优化后机构性能指标分布如图10所示。可以发现，整个平面内灵巧度均大于0.6，运动学性能较优化前有明显提升。

图11为尺寸优化后机构的DME指标分布情况，对比图7可以发现，机构动力学性能也得到了提升。

6 结论

(1)提出了一种冗余驱动的三平动并联机构，具有运动部分解耦的特点，可作为本体构造五轴打磨装置。

(2)采用螺旋理论和虚功原理建立了机构的动力学模型，并对关节驱动力进行了优化分配，驱动力理论分析与仿真计算结果最大偏差为0.6%，验证了模型的正确性。

(3)建立了灵巧度指标和动态可操作度椭球指标，并绘制了反映机构性能与尺度参数映射关系的性能图谱，得到了具有更优性能的机构尺度参数。