水稻秸秆反旋深埋滑切还田刀优化设计与试验

王金峰 张 鑫 唐 汉 王金武 翁武雄 杨东泽

(东北农业大学工程学院， 哈尔滨 150030)

0 引言

东北地区是中国水稻种植的主要区域。目前东北地区面临土壤板结退化，秸秆焚烧污染环境等问题[1-3]。秸秆还田可以提高土壤肥力、改善土壤结构，同时可有效减少农田秸秆焚烧，有利于农业的可持续发展[4-5]。但是由于东北地区特殊的地理环境，造成了秸秆量大、腐解缓慢的问题，普通旋耕机作业后导致秸秆埋入土层较浅，影响后续插秧工作[6]。根据相关农艺要求，秸秆还田率应大于85%，还田深度应大于18 cm，才能基本满足秸秆还田腐解要求[7]。

周勇等[8]研制的水田高茬秸秆还田耕整机采用双刀辊式螺旋刀，前置刀辊实现秸秆埋覆，后置刀辊实现秸秆的再次压埋，机具作业后能够满足秸秆还田的农艺要求，但存在机具重量过大的问题。王金武团队[6,9]提出一种水稻秸秆深埋还田技术，机具采用反旋作业方式，还田刀从底部开始向上切削土壤，更多的土壤因张力作用而破裂，作业后可以形成秸秆在下、土壤在上的理想作业环境，但存在功耗过大的问题。

本文针对上述问题，拟设计一种秸秆反旋深埋滑切还田刀，对还田刀结构参数进行理论分析及优化设计，在保证还田刀抛土能力的同时，增加还田刀的滑切性能，减少缠草现象，降低还田机作业时的功率消耗，运用离散元仿真软件EDEM探究还田刀与土壤-秸秆的作用机理，对比分析传统还田刀与滑切还田刀的作业指标，通过田间试验验证仿真结果的准确性，检验滑切还田刀在高含水率地块的作业效果。

1 反旋深埋滑切还田刀结构与工作原理

还田刀作为还田机的重要部件，其结构参数对还田机的作业效果和功率消耗有很大影响，图1为反旋深埋滑切还田刀的正视图与左视图。还田刀由侧切部分、正切部分和过渡部分组成，侧切刃与正切刃采用相同的阿基米德螺旋线设计，保证了侧切刃与正切刃的平滑过渡及刃口的滑切性能，侧切面为平面，主要用于切割破碎土壤，正切面为曲面，采用圆弧曲线设计，保证了还田刀的抛土能力与更小的切土功耗。还田刀的具体工作原理见文献[6]，传统还田刀正切刃先入土，侧切刃后入土，秸秆由正切刃向侧切刃滑动，容易缠绕在刀轴和还田刀柄端位置上，同时还田刀的入土冲击大、功耗大[10]，反旋深埋滑切还田刀在作业时侧切刃先入土，正切刃后入土，秸秆由侧切刃向正切刃滑动，不容易造成缠草现象，入土冲击小，同时刃口设计为楔形，降低切削阻力，减少切土功耗。

2 关键部件设计

2.1 还田刀刃口曲线设计

以还田刀的滑切角为主要设计指标，采用阿基米德螺旋线对还田刀刃口曲线进行设计[9-10]。还田刀刃口滑切角定义为刃口曲线任意一点的速度方向与该点法平面之间的夹角[11]。如图2所示，选取还田刀刃口曲线上一点M为动点进行分析，以地面为定参考系，刀辊轴为动参考系，点M绕刀辊轴的匀速圆周运动为相对运动，相对速度vr为点M的圆周速度，牵引运动为刀辊轴沿前进方向的匀速直线运动，牵引速度ve为还田机的前进速度，绝对速度va为相对速度vr与牵引速度ve的矢量和。还田刀能够将土壤与秸秆顺利脱出的滑切角为35°～55°[12]，由于反旋的作业方式，滑切还田刀的动态滑切角小于静态滑切角[13]，因此要保证反旋深埋滑切还田刀的滑切能力须使动态滑切角不小于35°。

假设机具作业时刀轴逆时针匀速旋转，机具匀速向右前进。对还田刀刃口动态滑切角方程进行求解，以x轴为起始点进行计算，则还田刀刃口曲线上任意一点可由方程表示为

(1)

用向量方程ρ表示刃口曲线上任意一点

ρ=r(φ)sinφi+r(φ)cosφj+z(φ)k

(2)

式中φ——刃口上任意点与x轴夹角，rad

r(φ)——刃口上任意点极径，mm

根据定义求解还田刀滑切角方程，需要先求解刃口曲线任意一点的切线方程

T=dρ/dφ=(r′(φ)sinφ+r(φ)cosφ)i+
(r′(φ)cosφ-r(φ)sinφ)j+z′(φ)k

(3)

此切线方程由曲线参数决定，应考虑机具前进速度对滑切角的影响，根据坐标平移与旋转公式得到还田刀跟随机具前进运动状态下的刃口曲线上任一点的矢径ρ*和切线方程T*为

ρ*=(vet+r(φ)sin(φ+ωt))i+
(r(φ)cos(φ+ωt))j+z(φ)k

(4)

T*=(r′(φ)sin(φ+ωt)+r(φ)cos(φ+ωt))i+
(r′(φ)cos(φ+ωt)-r(φ)sin(φ+ωt))j+z′(φ)k

(5)

式中ω——刀片端点M处角速度，rad/s

t——还田刀运动时间，s

刃口曲线上任一点的速度矢量va为

va=dρ*/dt=(ve+ωr(φ)cos(φ+ωt))i-
ωr(φ)sin(φ+ωt)j

(6)

根据滑切角的定义得知va和T*之间的夹角为刃口曲线动态滑切角τ′d的余角，即刃口曲线动态切割角γ′d，有

cosγ′d=cos(va,T*)=va·T*/(vaT*)

(7)

(8)

令α=φ+ωt，r′=r′(φ)=dr(φ)/dφ，r=r(φ)，z′=z′(φ)=dz(φ)/dφ，将公式(8)代入公式(7)得

(9)

根据三角函数关系，某角的正切值与余弦值存在关系

(10)

将公式(9)代入公式(10)得到动态切割角γ′d正切值表达式为

(11)

因此，动态滑切角τ′d的表达式为

(12)

当z′=0时，式(12)表示的是侧切刃曲线的动态滑切角τd，即

(13)

当还田机作业时，刃口曲线上各点的绝对速度va与相对速度vr之间存在一个夹角Δτ，Δτ为滑切还田刀的动态滑切角与静态滑切角的差值，根据三角函数关系

(14)

求解得

(15)

已知还田机最佳作业条件为前进速度选用低速一挡(1.5 km/h)，刀辊转速选用250 r/min，根据公式(15)可知：当前进速度ve越大，刀轴角速度ω越小时，Δτ越大，滑切还田刀的动态滑切角越小，相反当前进速度ve越小，刀轴角速度ω越大时，Δτ越小，滑切还田刀的动态滑切角越大，因此选用前进速度为3 km/h，刀辊转速为190 r/min的作业条件为临界条件进行刃口曲线设计，保证滑切还田刀在低刀辊转速、高前进速度的工况下满足滑切条件，设计的阿基米德螺旋方程为

r=2.703 2φ+19

(16)

方程求导得r′=2.703 2 mm/(°)=154.91 mm/rad。

将设计的侧切刃刃口曲线(式(16))代入公式(13)、(15)进行求解，考虑秸秆深埋还田时对耕深的要求，选取还田刀侧切刃起始点位置r为126.7 mm，终点位置r为196.5 mm，从中按比例选取8个点求解，如表1所示。

表1 侧切刃各角度计算值Tab.1 Calculated values of various angles of side cutting edge

由计算结果可知，所设计的侧切刃动态滑切角由刀柄部至刀端部逐渐增大，侧切刃起点位置的滑切角略小于35°，已知刀盘半径为120 mm，在实际工作过程中可认为侧切刃起始点位置并不切割土壤，其余各位置均满足还田刀的滑切条件。

2.2 还田刀正切面设计

传统还田刀多采用平面正切面，此类型正切面不能兼顾切土与抛土能力，采用曲面设计正切面可以解决此问题，使用曲母线构造正切面，可用圆弧作为正切面母线[14]。

如图3所示，设正切刃上任意一点坐标为(x，y，z)，圆弧母线的圆心坐标为(x0，y0，z0)，圆弧半径为rθ，在任意平行于侧切刃的切面内，圆弧母线方程为

(17)

圆弧圆心坐标为

(18)

式中η——正切刃任意点切线与y轴夹角

由图3得各角度之间存在关系

(19)

式中ψ——正切刃任意点处的安装角

将式(1)、(18)、(19)代入式(17)得

X2+Y2-2r(φ)rθcos(2φ-ψ)-
2x(r(φ)sinφ+rθsin(φ-ψ))-

2Y(r(φ)cosφ-rθcos(φ-ψ))+r2(φ)=0

(20)

式(20)为还田刀正切面圆弧母线方程，为保证还田刀侧切刃与正切刃的滑切性能与平滑过渡，防止刃口曲线曲率突变导致还田刀滑切性能降低出现缠草现象，正切刃使用与侧切刃相同的阿基米德螺旋线进行设计，正切面的设计要求为：保证还田刀抛土性能的同时减少还田刀切土功耗。还田刀的耕宽由正切面决定，耕宽过小还田刀抛土性能降低，严重时会造成漏耕现象，耕宽过大还田刀抛土性能提高，但不利于滑切脱草，增加还田刀作业功耗，已知还田机两刀盘之间的距离为242 mm，为探究不同圆弧半径与耕宽的关系，首先选取rθ为50、60、70、80、90 mm 5种情况对还田刀耕宽进行计算分析，确定圆弧半径范围。耕宽分别为113.0、111.4、105.0、86.6、80.9 mm。随着rθ增大耕宽逐渐减小，由于土壤之间的黏结作用，还田刀在高速转动过程中左侧还田刀与右侧还田刀之间可预留10～20 mm距离，可以在保证还田刀抛土能力的同时为秸秆和土壤滑脱出还田刀提供一定的空间，因此理想的还田刀耕宽为111～116 mm，选择rθ为50 mm或60 mm，且最大不超过60 mm。

正切面安装角为正切面的主要参数之一，安装角越大切土阻力越小，但抛土、覆盖能力变差[15]，为进一步确定rθ的取值，对还田刀正切面安装角进行分析，使用Creo 5.0软件对两种不同rθ的还田刀正切面安装角进行测量，rθ=60 mm时的数据记为A组，rθ=50 mm时的数据记为B组，结果如表2所示。

表2 两种圆弧半径的滑切还田刀正切面安装角测量结果Tab.2 Measurement results of installation angle tangent section of two kinds of slip-cutting straw returning blade with arc radius

由表2可以得出，两种不同半径的圆弧母线测量的刃口极径基本一致，圆弧母线半径为60 mm时的安装角普遍大于圆弧母线半径为50 mm时的安装角，在允许最大安装角的范围内，安装角越大还田刀的功耗越小[15]，在Z轴坐标值由0过渡至80 mm过程中，两种不同半径的圆弧母线安装角变化幅度不大，变化规律都是先增大后减小，rθ=60 mm时，安装角最大为42.4°，最小为39.2°，rθ=50 mm时，安装角最大为41.8°，最小为39.1°，说明两种不同半径的圆弧母线正切面在前段和中段基本一致，不能作为选择依据，但在80 mm过渡至90 mm过程中，ψA由41.5°变化至40.8°，降低0.7°，ψB由40.3°变化至33.7°，降低6.6°，分析原因为：在还田刀长度确定的情况下，圆弧半径过小会导致还田刀正切面末段回转过大，此情况下还田刀正切面形成U型，不利于还田刀抛出土壤，更不利于秸秆从正切刃滑出，增大了切土阻力，不利于秸秆还田，综上所述选择圆弧母线半径为60 mm设计正切面，此时正切面满足耕宽要求，且正切面安装角较大，切土功耗最小，在保证还田刀抛土能力的同时最大限度地降低切土功耗。

3 离散元模型建立与仿真分析

湿黏水稻土的还田刀-土壤-秸秆互作规律比较复杂，可通过离散元软件EDEM进行仿真分析[16]，以还田刀作业时的功耗和秸秆还田率为主要评价指标，结合多因素试验分析影响还田刀作业功耗的主要因素，为后续田间试验验证奠定基础。

3.1 还田刀模型建立

使用Creo 5.0软件建立还田刀及刀盘三维模型(比例1∶1)，为了简化仿真计算量，以.step格式导入EDEM软件，选用merge命令使模型为一个整体[17]，如图4所示。设置还田刀及刀盘模型材料属性为65Mn钢，泊松比为0.35，剪切模量为7.8×1010Pa，密度为7 850 kg/m3[18]。

3.2 土壤模型建立

土壤颗粒的大小和形状比较复杂，为了简化仿真计算量和时间，在保证仿真可靠性前提下，采用半径为5 mm的球形颗粒模拟土壤颗粒[19-21]。

由于湿黏土壤的黏结力比较大，选用Hertz-Mindlin with bonding接触模型模拟土壤颗粒间、土壤颗粒与还田刀、土壤颗粒与秸秆颗粒的黏结、内聚、摩擦及破碎等关系[22-24]，该颗粒接触模型具有5个参数，分别是：黏结法向刚度sn与黏结切向刚度sτ、黏结法向临界应力σmax与黏结切向临界应力τmax及颗粒黏结半径Rb，合理设置5个参数可以模拟水稻土壤黏性特征[25-26]，取sn=sτ，σmax=τmax，可以简化参数标定[26-27]，取黏结切向刚度为5×107N/m3[25-26]，以土壤宏观剪切、压缩破坏强度为参考，确定耕作层、底层土壤颗粒黏结强度的临界应力分别为3×105Pa和5×105Pa[25-26]，土壤颗粒黏结半径由土壤的含水率和密度计算得出，为了进一步模拟真实土壤环境，设置土槽尺寸为1 000 mm×500 mm×400 mm，0～150 mm为土壤耕作层，150～300 mm为土壤底层[28]，仿真参数见表3[16-18,20-21]。

表3 土壤及还田刀离散元模型接触参数Tab.3 Contact parameters of discrete element model of soil and straw returning blade

3.3 秸秆模型建立

建立柔性秸秆模型较为复杂[29]，在水稻收获机收获后，秸秆多被粉碎为100 mm以下的小段秸秆，还田刀多数情况下对秸秆形成扰动作用而不是切割[29]，故采用13个直径为5 mm、球心间隔为4 mm的秸秆颗粒组成长53 mm的秸秆模型，根据实际收获机收获后地表秸秆覆盖量为336～353 g/m2，设置秸秆颗粒生成数量，具体仿真参数见表4[30]。

表4 秸秆离散元模型接触参数Tab.4 Contact parameters of straw discrete element model

图5a为EDEM建立的仿真土槽及秸秆模型，由上至下依次为秸秆层、耕作层和底层，图5b为土壤颗粒间bond键。

3.4 虚拟仿真过程及结果分析

在虚拟作业过程中，设置滑切还田刀从土槽左侧以1.5 km/h的速度匀速向右前进，以250 r/min

的转速匀速反旋切割土壤，设置固定时间步长为5.76×10-5s，即Rayleigh时间步长的10%，单元网格尺寸设置为颗粒平均半径的3倍，总仿真时长15 s，每0.01 s保存一次仿真数据[18]。

选取14.01 s时仿真结果，对底层土壤颗粒运动进行分析，将土壤颗粒分为4个区域，如图6所示，将土壤颗粒按速度分为3个等级，3.75×10-14～0.7 m/s为低速颗粒，0.7～2.1 m/s为中速颗粒，2.1～3.5 m/s为高速颗粒，以网格划分土壤颗粒并分别计算各等级颗粒数量为243、1 403、745。

对区域1颗粒运动趋势进行分析，如图7a所示，底层土壤颗粒受还田刀作用后，有向各个方向的运动趋势，多数颗粒向还田机前方运动，这些颗粒落地后造成还田机前方壅土，还田刀会重复切削此区域颗粒导致功耗增加，因此该区域颗粒越少越有利于还田机作业功耗的降低。

如图7b所示，区域2颗粒为还田刀边缘的土壤颗粒，在加速过程中提前脱离还田刀后，有向前和向下的运动趋势，向前运动的土壤颗粒撞击罩壳后，一部分黏附在罩壳上，另一部分被反弹后与向下运动的土壤颗粒落于还田机前方形成壅土，因此合理设计前罩壳曲线可以在一定程度上减少机具前方壅土现象，达到降低功耗的目的。

如图7c所示，区域3土壤颗粒受还田刀正切面摩擦力作用先加速至与还田刀速度相同，后随还田刀一起匀速运动，土壤颗粒速度较大，具有向上和向后运动的趋势，此区域土壤颗粒越多说明滑切还田刀的抛土性能越好。

如图7d所示，区域4土壤颗粒的运动可近似为抛物线运动，在运动过程中，较轻的秸秆颗粒动能小，先于土壤落下，土壤颗粒覆盖在秸秆上，以此实现秸秆的深埋还田。

图8为耕作层土壤颗粒仿真结果，按上述分区方法对耕作层土壤进行分析，土壤颗粒的运动趋势与底层土壤颗粒基本一致。

计算各个区域土壤颗粒数量及不同速度土壤颗粒比例，如图9所示。将区域1和区域2土壤颗粒数所占耕作区总土壤颗粒数的比例称为壅土比例，为26.7%，此部分土壤颗粒所占比例越低，还田机因重复切削所消耗的功耗越低；将区域3和区域4土壤颗粒所占耕作区总土壤颗粒数的比例称为抛土比例，为73.3%，此部分土壤颗粒所占比例越高，还田机抛土性能越好。以壅土比例和抛土比例作为衡量还田刀作业效果的指标之一。

如图10，以秸秆还田率为衡量还田刀作业效果的另一指标，在已耕作区域将埋入土壤的秸秆颗粒标记为红色，计算埋入土壤的秸秆颗粒占耕作区域总秸秆颗粒数的比例为95.3%，满足秸秆还田的作业指标，由图可以看出，还田机作业后，底层土壤与耕作层土壤混合均匀，可以改善土壤结构，提高蓄水能力，有利于水稻产量的提高。

导入传统还田刀模型进行仿真对照试验，14 s时仿真结果如图11，分析计算作业后秸秆还田率为95.8%，统计耕作层与底层的各区域土壤颗粒数量并计算抛土比例，结果如表5。

表5 不同区域颗粒数量及比例Tab.5 Number and proportion of particles in different regions

对传统还田刀与滑切还田刀的作业功耗进行对比分析，导出12～14.5 s还田刀功耗如图12所示，还田刀功耗呈现一定的规律性：12～12.9 s时，还田刀由空转开始切土，还田刀功耗逐渐增大，主要用于侧切刃破碎土壤颗粒和正切面运送土壤颗粒；12.9～13 s时，还田刀功耗呈下降趋势，分析原因为部分不稳定土壤颗粒未加速至与还田刀速度相同而提前抛出，形成区域1颗粒；13～13.1 s，还田刀做功用于土壤颗粒重力势能和动能的增加，虽然仍有部分土壤颗粒脱离还田刀形成区域1和区域2，但还田刀总体功耗仍然呈增大趋势，且还田刀功耗逐渐达到最大值；13.1～13.5 s时，还田刀向后抛送土壤颗粒，大部分土壤颗粒被抛向后方，还田刀功耗迅速减小至最低后开始下一次运送土壤颗粒过程。

仿真结果表明，所设计的秸秆反旋滑切还田刀耕作层土壤颗粒抛土比例为73.3%，底层土壤颗粒抛土比例为74.3%，传统还田刀耕作层抛土比例为75.6%，底层土壤颗粒抛土比例为76.5%，差值分别为2.3、2.2个百分点，可认为两种还田刀抛土性能基本相同；在相同耕作区域以红色表示埋入土壤的秸秆颗粒，以黄色表示未埋入土壤的秸秆颗粒，计算两种还田刀作业后还田率分别为95.3%和95.8%，均满足秸秆还田的农艺要求；计算秸秆反旋滑切还田刀的每秒平均功耗为851.6 J，传统还田刀的每秒平均功耗为1 041 J，每秒平均功耗降低了18.19%，所设计的秸秆反旋滑切还田刀在保证还田刀抛土性能的同时，提高了还田刀的滑切性能，降低了还田机作业功耗。

3.5 虚拟仿真多因素试验

影响还田机作业功耗的主要因素有：还田机前进速度、刀辊转速和留茬高度。在其他条件不变的情况下，机具前进速度过大，切土节距变大，碎土率和地表平整度降低；由于反旋的作业方式导致刀辊转速过高时，机具的功耗增大，刀辊转速过低导致向后抛土率降低，机具前方壅土，重复切削土壤导致功耗增大；留茬高度过高容易导致机具刀辊缠草，功耗增大。

为探究影响还田机作业功耗的主要因素，进行三因素三水平的正交试验设计，根据拖拉机实际作业条件[31]及文献[6，9]的机具作业条件，设计试验因素编码见表6。仿真试验结果见表7。

表6 试验因素编码Tab.6 Codes of experiment factors

表7 仿真试验设计与结果Tab.7 Simulation test design and results

运用Design-Expert软件进行分析得到还田机功耗的二次多项式回归模型为

Y=98.60+0.04A-0.46B-5.55C-8.16×
10-5A2+1.06×10-3B2+0.55C2+1.39×
10-6AB+1.11×10-4AC+0.02BC

(21)

对回归模型进行方差分析，结果见表8，模型的P值小于0.000 1，表明回归模型高度显著，模型失拟项P值为0.584 4，大于0.05，模型的失拟性不显著，模型拟合程度高；预测R2(0.828)与调整R2(0.941 2)差值小于0.2，两者基本一致，精度测量信噪比为20.712，比率大于4，说明模型具有较高的可靠性。由表中数据可知刀辊转速与机具前进速度对还田机功耗影响极显著，留茬高度对还田机功耗影响显著，影响从大到小依次为：刀辊转速、机具前进速度、留茬高度。

表8 还田刀功耗二次多项式模型方差分析Tab.8 Analysis of variance of quadratic polynomial model for power consumption of straw returning blade

绘制各因素交互效应响应曲面图。由图13a可知，在留茬高度为200 mm时，随着刀辊转速和机具前进速度的增加，机具功耗逐渐增大，刀辊转速的增大速率约为机具前进速度的两倍。由图13b可知，在前进速度为2.25 km/h，留茬高度在140～260 mm范围内，还田机功耗随着刀辊转速的增加呈现先减小后增大的趋势，在刀辊转速较低时，抛土性能降低导致机具前方壅土，功耗较大，在190～205 r/min范围内随着刀辊转速的提高，抛土性能提高，功耗减小，在205～250 r/min范围内，功耗随着刀辊转速的提高逐渐增大，且增大速率逐渐增大，在刀辊转速较高时，留茬高度的变化对机具功耗的影响较小。

4 田间试验

4.1 试验方法

为检验水稻秸秆反旋深埋滑切还田刀的田间作业效果，样刀加工安装完成后于2020年9月24日在黑龙江省佳木斯市桦川县玉成农场水稻种植基地，以及于2020年10月19日在佳木斯市前进镇前进农场进行了秸秆还田田间试验。

桦川县玉成农场田间试验时间较早，属于提前收获后直接进行秸秆还田作业，秸秆和土壤含水率较高，其环境并不适宜进行秸秆还田作业，两田间试验地点的作业环境及工况条件见表9。两地田间试验效果如图14所示。

表9 作业环境及工况条件Tab.9 Working environment and working conditions

根据NY/T 499—2013《旋耕机作业质量》，测量并记录作业后耕深、还田率及地表平整度，秸秆还田率测试方法为：在未作业区域从对角线等间距选取5点作为测量点，每点分别选取1 m2测量，收集地表的秸秆称量记为M1，M2，…，M5(g)，还田机作业后，在已经作业区域选取相同5点测量地表上秸秆，记为m1，m2，…，m5(g)，还田率ε计算式为

(22)

地表平整度测量方法为：过耕后地表线的最高点，垂直于还田机前进方向作一水平直线为基准线，选取大于还田机幅宽的宽度分成10等份，在等分点上作垂线与地表相交并测量各交点至基准线的距离记为hi，则地表平整度h计算式为

(23)

4.2 结果与分析

分别记录两次田间试验数据并代入式(22)、(23)计算秸秆还田率及平整度，表10为两试验地点还田率、平整度和耕深对比。

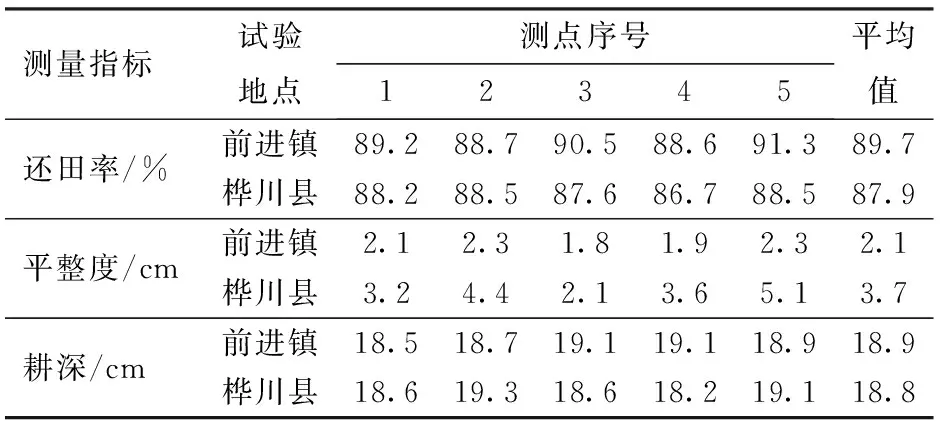
表10 试验指标对比Tab.10 Comparison of test indexes

前进镇田间试验的秸秆还田率平均值为89.7%，桦川县田间试验的秸秆还田率平均值为87.9%，将田间试验结果与EDEM仿真试验结果进行比较，还田率相对误差为6.29%和8.42%，分析原因为：在土壤含水率较高时，部分秸秆与土壤混合后很难分离，无法先于土壤落地形成秸秆在下、土壤在上的结构。基于以上分析认为各指标相对误差在允许的范围内，验证了还田刀设计及仿真分析的可行性和合理性，实际测量的还田率出现波动，分析原因为收获时秸秆抛撒不均匀导致不同测量点的秸秆覆盖量不同，在秸秆覆盖量较大的测量点，还田率较低；另一方面在实际作业过程中，受田间地块条件及人为因素等影响，还田机前进速度及刀辊转速会有小幅度变动，从而影响秸秆还田率。

前进镇田间试验的平整度平均值为2.1 cm，桦川县田间试验的平整度平均值为3.7 cm，计算两组数据方差为0.041 6和1.053 6，前进镇的作业后地表平整度稳定性好，分析原因为土壤含水率较低时，机具的碎土效果好，大块土壤撞击挡草栅后先落地，小块土壤穿过档草栅后，覆盖在大块土壤上，地表平整；土壤含水率较高时，大块土壤堵塞挡草栅，导致部分小块土壤无法穿过挡草栅，无法形成大块土壤在下、小块土壤在上的结构。

前进镇田间试验的耕深平均值为18.9 cm，桦川县田间试验的耕深平均值为18.8 cm，两次田间试验耕深基本一致，方差分别为0.054 4和0.161 6，桦川县田间试验耕深稳定性相对于前进镇较差，原因为在土壤含水率较高时，拖拉机下陷严重导致耕深不稳定。

由试验结果可知：所设计的深埋滑切还田刀在含水率为25%～30%的地块作业时，还田率为87.9%，地表平整度为3.7 cm，耕深为18.8 cm；在含水率为20%～25%地块作业时，还田率为89.7%，地表平整度为2.1 cm，耕深为18.9 cm，均满足秸秆还田的农艺要求。

5 结论

(1)设计了一种水稻秸秆反旋深埋滑切还田刀，在减轻水稻秸秆全量深埋还田机作业时刀辊前方壅土现象的同时，增加了还田刀的滑切能力，每秒平均功耗降低了18.19%。

(2)根据土壤及秸秆各项物料参数，运用离散元软件EDEM建立颗粒模型，并进行秸秆深埋还田仿真试验，分析了土壤抛运规律，验证了滑切还田刀的抛土性能和滑切性能，仿真作业后还田率与传统还田刀还田率基本一致，对还田刀作业功耗进行分析，正交试验表明，还田机功耗受刀辊转速影响最大。

(3)通过田间试验，对比分析了滑切还田刀在不同含水率地块的3项作业指标，验证了滑切还田刀的作业效果及仿真试验的可靠性，试验结果表明：在土壤含水率为20%～30%，地表秸秆覆盖量为336 ～353 g/m2，拖拉机作业速度为低速一挡(1.5 km/h)，刀辊转速为250 r/min时，秸秆深埋滑切还田刀作业后，平均耕深为18 cm左右，还田率为87.9%～89.7%，地表平整度为2.1～3.7 cm，作业指标均满足秸秆还田的农艺要求。