带分流叶片混流式水泵非定常流动特性研究

张 旭 王鹏飞 阮晓东

(1.浙江大学流体动力与机电系统国家重点实验室， 杭州 310027；2.浙江大学自贡创新中心， 自贡 643000)

0 引言

混流式水泵广泛应用于多种领域[1-4]。混流式水泵高速旋转的叶轮与静止的导叶之间的动静干涉相互作用、压水室壁面压力波动反射作用以及正常运行过程中主泵内部复杂的三维非定常流动等，都会引起泵内的压力波动[5-7]，强烈的压力脉动不仅会对泵的流量、扬程和效率等外特性产生影响，而且会引起泵叶片载荷波动[8]，进一步引发机组设备的振动和噪声[9-10]，对泵的安全平稳运行产生不利影响。因此很有必要对混流泵内流场的压力脉动特性及其叶片载荷特性进行深入研究。

随着计算机技术的突飞猛进，计算流体力学(Computational fluid dynamics, CFD)和流固耦合(Fluid solid interaction, FSI)已经成为流体机械的内部流动研究及关键部件应力应变分析的有效技术手段之一[11-14]。文献[15]采用大涡模拟方法对高比转数混流泵内三维非定常湍流场进行了数值模拟，发现压力脉动幅值从轮毂到轮缘均逐渐增大，叶轮进口压力脉动无明显规律性，但出口存在明显的周期性。文献[16]研究了混流泵内以叶片压力脉动为声源诱发的噪声，研究发现混流泵叶轮和蜗壳之间的动静干涉作用是引发流动诱导噪声的主要原因;流动诱导噪声的主频是由压力脉动主频以及泵体结构的固有频率综合决定的。泵内非定常流动会对泵叶片产生交变载荷，泵关键部件的应力与流固耦合分析对其安全运行至关重要。文献[17]采用单向流固耦合对离心泵叶轮进行结构分析，研究发现在各工况下叶轮应力分布不均且存在局部应力集中；叶轮变形的总位移随半径的增大不断变大，并在叶轮边缘达到最大。文献[18]对比分析了顺序耦合和双向耦合发现叶轮上的等效应力分布基本一致。文献[19]利用CFD和有限元分析软件对单叶片离心泵采用单向和双向流固耦合计算，分析了转子振动位移和所受的水力激励，并与试验测量的水力激振位移对比。但上述研究对象多为离心泵，对混流泵的流固耦合研究还需深入。

分流叶片采用了长短叶片间隔布置，可以有效地改善叶轮内部流场分布，可以综合提高泵的整体性能，国内外学者对带分流叶片的离心泵进行了大量的数值模拟和试验测试[20-23]，但应用在混流泵上还鲜有报道。本文基于计算流体力学软件Fluent 16.0和ANSYS Workbench 16.0平台对混流泵的内部流动及流固耦合特性进行计算，主要研究叶轮流道内有/无分流叶片对混流泵性能的影响。

1 研究方法

1.1 计算模型与网格划分

某型号混流式水泵的设计参数为：流量Q=1 386 m3/h，扬程H=16 m，转速n=1 500 r/min，比转数为392.5。泵的结构是长轴悬臂式安装结构。设计了两个叶轮方案，其中方案1为6叶片原始混流泵叶轮结构，方案2是在方案1的基础上进行优化，在流道中加入了分流叶片，分流叶片通过截短主叶片生成。分流叶片长度为主叶片长度的1/2。导叶选11片。混流泵的全三维结构如图1所示。输送的介质为常温清水，密度1 g/cm3,粘度1 Pa·s，模型泵叶轮和轴的材料为结构钢，密度7 850 kg/m3,弹性模量210 GPa,泊松比0.3。

采用ICEM-CFD软件对模型进行网格划分，选择网格类型为非结构化四面体网格。为保证网格质量和计算精度，对几何模型曲率较大处进行了局部网格加密。在验证了网格无关性要求后，流体域选择的总网格数为430万。各个部件的网格划分如图2所示。固体区域的有限元网格在Transient Structure中生成，网格单元数为341 577。

1.2 数值计算方法

采用ANSYS Fluent软件对流场进行数值计算，采用标准k-ε湍流模型进行求解。采用基于隐式耦合求解的SIMPLE算法求解时均N-S(Navier-Stokes)方程。旋转叶轮和静止导叶之间的耦合采用滑移网格模型，采用Frame motion和Mesh motion处理旋转叶轮网格的稳态计算和瞬态计算过程。进口边界采用质量流量入口，出口边界条件采用压力出口。壁面设置为无滑移固定壁面，壁面区采用壁面函数法处理。在导叶流道内沿着流道设置3个压力脉动监测点。监测的位置如图3所示。计算时首先对整个泵进行稳态数值计算，并将收敛的稳态结果作为初始值进行瞬态数值计算。在作瞬态数值计算时，设置时间步长为2.22×10-4s[24]。每个时间步长叶轮旋转2°，旋转一周需要180个时间步长。收敛残差为10-5。

由于本文需要考虑叶片变形与流场作用的双向流固耦合效应，所以在作流场瞬态计算时，采用动网格技术来处理流固耦合面的网格变形，本文采用光顺模型和网格重构方法来进行动网格的变形。在固体求解域中将叶轮叶片选为流固交界面。采用ANSYS Workbench平台提供的system coupling模块进行数据交换。流场的输出参数为力载荷，输入参数为网格变形量，结构场的输出参数为网格变形量，输入参数为力载荷。每一步都进行数据交换，耦合收敛残差设为0.01。

1.3 外特性验证

为了验证当前数值计算的准确性，在闭环试验台中进行了原始模型泵的外特性试验。当采用CFD计算泵的效率时，忽略了其机械损失和容积损失，因此在换算成实际效率时需要加上一个损失系数。根据泵设计手册[25]，机械损失和容积损失定义为0.96和0.96，图4中HD表示设计扬程，QD表示设计流量，η表示效率。图4显示了试验与经过修正的数值计算结果的H-Q以及η-Q的外特性曲线比较。可以看到，CFD计算结果与试验结果吻合较好，CFD计算可以较为精确地预测曲线的趋势，CFD计算的扬程和效率与试验之间的相对误差小于5%，CFD计算结果与试验结果的差异可能是由网格分辨率不足引起的，要准确捕捉叶片表面周围的湍流边界层需要更为复杂的网格模型和计算方法，本文的重点并不是湍流精确计算方法，当前采用的数值计算方法可以满足研究需求。同时对比方案1和方案2的外特性曲线可以发现，两种设计方案的模拟扬程都能满足设计要求。在设计点附近，方案2的扬程和效率与方案1相近并稍微有所提高，在小流量工况下，方案2的扬程和效率明显高于方案1，这主要是因为在小流量工况下分流叶片的添加使得叶轮流速分布更加均匀，控制了内部流动分离，流道内回流引发的流动损失减小。在大流量工况下，方案2的扬程和效率明显低于方案1，这主要是因为在大流量工况下分流叶片的添加带来了排挤阻塞作用。另外从效率曲线上可以看出，在设计点左侧，方案2的效率下降速度比方案1慢，方案2的高效区更宽，说明分流叶片的添加有利于泵的多工况尤其是小工况运行。表1给出了各过流部件在设计工况下的总压(压力水头)损失占扬程的百分比。从表中可以看出，泵内主要水力损失发生在叶轮和压水室中，方案2中分流叶片的添加虽然使得叶轮的水力损失增加，但其使得其他过流部件内的水力损失减小，综合来看，在最佳效率点方案2中总的水力损失更小，效率更高。

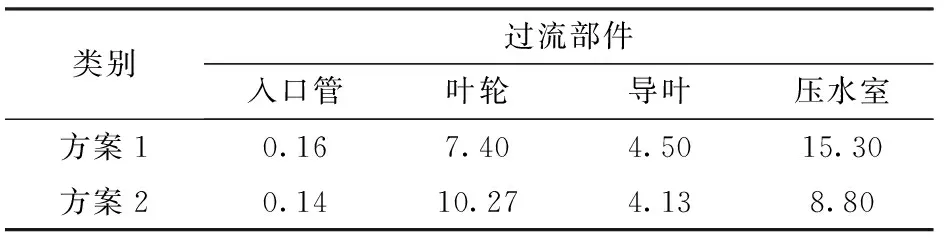
表1 设计工况下各过流部件总压损失占扬程百分比Tab.1 Total pressure loss of each component under design condition %

2 计算结果与讨论

2.1 压力脉动对比分析

为了探究分流叶片的添加及流固耦合效应对混流泵内压力脉动的影响，图5～8对比分析了导叶流道内点P1～P3的压力脉动的时域和频域。可以发现，在考虑了流固耦合效应后，混流泵内压力脉动幅值都有较为明显的提高，具体来看，方案1中原始叶轮结构混流泵内压力脉动的主频为叶频150 Hz，考虑流固耦合效应后基频及其倍频幅值都有较大幅度提高，方案2中带分流叶片混流泵内压力脉动的主频为全叶频300 Hz,但由于分流叶片长度只有正常叶片1/2，所产生的压力脉动叠加于原始脉动分量上，削弱了原始叶轮脉动强度，由于分流叶片长度与正常叶片不同，其引发的压力脉动频率分量也存在半叶频150 Hz,但幅值明显低于主频300 Hz。考虑流固耦合效应后，压力脉动的主频300 Hz处的脉动幅值大为提高，但其半叶频150 Hz处的脉动幅值大为减小。这说明流固耦合效应削弱了分流叶片长度的影响，使得分流叶片产生的尾迹与正常长度叶片的尾迹更为接近。对比两种方案的压力脉动数据可以发现，分流叶片的存在，有效地削减了动静叶干涉产生的压力脉动幅值。点P1处的压力脉动主频幅值从7 908 Pa/4 335 Pa(考虑流固耦合/无流固耦合)下降到4 304 Pa/1 829 Pa,降幅达到45.6%/57.8%，但沿着流道方向其脉动削减程度逐渐下降。出口处方案2的脉动水平相比方案1还有所上升，这说明分流叶片的添加会使得导叶内脉动耗散衰减的速度变慢。但从疲劳S-N(应力-寿命)曲线来说，低幅值脉动增加不会影响叶片寿命，高幅值脉动的削减使得叶片所承受的高周应力大幅降低，可以有效提高叶片寿命。所以分流叶片的设计削减了压力脉动最大幅值，有利于叶片的安全承载。

2.2 叶轮径向力轴向力分析

图9展示了分流叶片的添加及流固耦合效应对混流泵径向力的影响，从图9中可以看出，在不考虑流固耦合效应时，分流叶片的添加使得径向力的平均水平从100 N提高到140 N，径向力的脉动幅值从76 N增大到125 N，但径向力脉动的主频并未发生改变。考虑流固耦合效应时方案1原始叶轮的径向力变化较大，说明分流叶片的添加削弱了流固耦合作用对径向力的影响。图10展示了分流叶片及流固耦合效应对混流泵轴向力的影响，可以发现，在不考虑流固耦合作用时，方案1和方案2的轴向力基本保持不变，随时间波动幅度很小。且两种方案的轴向力比较接近，都在9 500 N附近。这说明添加长度为主叶片1/2长度的分流叶片对轴向力影响很小，基本不改变叶轮的轴向力。对比两种方案的流固耦合效应可以发现，考虑流固耦合效应时轴向力的平均水平都比不考虑流固耦合效应时低，脉动水平比不考虑流固耦合效应时有所提高，同样可以发现分流叶片的添加削弱了流固耦合作用对轴向力平均水平的影响。

2.3 转子应力及形变分析

在叶轮叶片固体结构上布置了6个测点，测点1位于叶轮出口靠近上盖板处，测点2位于叶轮出口中间，测点3位于叶轮出口靠近下盖板处，测点4位于叶轮进口靠近上盖板处，测点5位于叶轮进口中间，测点 6位于叶轮进口靠近下盖板处。图11、12为6个测点在一个周期内的等效应力变化曲线。可以发现，有无分流叶片对叶轮出口上盖板处的应力影响不大，两者基本重合。在叶轮出口中间和靠近下盖板处，分流叶片的存在使得其应力平均水平和应力变化幅值均下降。在叶轮进口靠近上盖板处，分流叶片的存在使得应力平均水平提高较多，而在叶轮进口中间和靠近下盖板处，分流叶片的存在使得应力平均水平下降。总体看来，分流叶片的添加可以降低应力变化幅值，在低应力测点，分流叶片的存在可能使得其应力水平上升，但在高应力测点处，分流叶片的存在使得其应力水平下降，这有利于混流泵的长期安全承载。图13、14是6个监测点在一个周期内的变形量曲线。可以看出，由于分流叶片的存在，叶片形变出现了一些相位差，分流叶片使得形变出现滞后。随时间变形量变化趋势基本一致，形变平均水平基本保持不变，但在某些位置分流叶片的添加使得变形量变化幅值明显降低。可以看出变形量级基本在0.1 mm左右，但由于水的可压缩性较小，所以如此小量级的形变引起压力脉动幅值如图6、8中所示成倍增加。

2.4 转子瞬态应力及形变分布

图15是方案1原始叶轮结构在一个周期内不同时刻的应力分布云图，图16是方案2带分流叶片叶轮结构在一个周期内不同时刻的应力分布云图。可以看出，原始叶轮叶片的应力沿着半径交替出现高应力区和低应力区。高应力区出现在叶片靠近轮毂处、叶轮中间和叶轮轮缘处；低应力区主要分布在轴心处。应力区域在叶片上呈长条结构。各时刻转子的应力分布图基本一致，均呈中心对称分布。带分流叶片叶轮的应力分布与原始叶轮应力分布有较大差别，其高应力区扩大，低应力区缩小，应力变化梯度减小，应力分布由长条结构变为渐缩的纺锤结构，整个叶片应力分布更加均匀。带分流叶片叶轮整体最大应力相比于原始叶片由25 MPa左右下降到17 MPa左右。这说明分流叶片不仅有利于提高转子叶轮的承载能力，而且有利于提高转子的抗疲劳特性。图17是方案1原始叶轮结构在一个周期内不同时刻的变形量分布云图，图18是方案2带分流叶片叶轮结构在一个周期内不同时刻的变形量分布云图。可以看出，变形量随着半径的增大而增大，但变形量在圆周方向并不是均匀分布的，最小形变的中心位于一个变化的偏心位置，偏心的产生与压水室的非均匀流动有关。最大形变位于叶轮出口靠近上盖板处。带分流叶片叶轮的变形量明显小于原始叶轮叶片变形量，这主要是由于分流叶片的添加使得压力脉动水平降低，从而使得作用在叶片上产生的应力水平降低，所导致的形变减小。另外可以观察到带分流叶片叶轮的形变在圆周方向分布的均匀性更好，最小形变中心的偏心距离明显减小。这主要是由于分流叶片的添加使得叶轮流道内的流动更加均匀，改善了形变在圆周方向的均匀性。

3 结论

(1)在设计点处保持扬程基本不变的情况下，分流叶片的添加减小了小流量工况的流动损失，提高了泵的效率。

(2)分流叶片的添加使得动静干涉产生的压力脉动幅值的最大值大幅降低，但减小了压力脉动衰减的速度。

(3)分流叶片的添加可以降低应力以及形变的波动幅值，高应力区主要集中于靠近叶轮轮毂及轮缘处，分流叶片的添加使得叶片最大应力减小，且改善了应力变化梯度，使得应力分布更加均匀，有利于混流泵叶片的安全承载。分流叶片的添加也使得叶片形变在圆周方向更加均匀，改善了形变分布的偏心问题。

(4)分流叶片的添加基本不影响混流泵的轴向力平均值，两种方案下的轴向力的脉动水平都比较低。分流叶片的添加使得混流泵径向力平均水平和脉动幅值有所升高，但并未改变径向力脉动主频。