应对反应攻击的级联中密度准循环奇偶校验码公钥方案
巫光福,戴子恒
(江西理工大学信息工程学院,江西赣州 341000)
0 引言
当今,世界各国都在如火如荼地研究着量子计算。量子计算机具有超强的计算能力,能在相对较短的时间内处理大量的数据,这给基于计算复杂度的现代公钥密码学(Public Key Cryptography,PKC)的安全带来了巨大挑战。为应对量子计算带来的威胁,后量子密码学[1]应运而生。目前,美国国家标准技术研究所(National Institute of Standards and Technology,NIST)正制定新一代的后量子密码方案标准[2],其主要分为基于格、基于编码、基于多变量和基于哈希这四类构造方法。
McEliece 型的加密方案[3]是基于编码的公钥密码中最经典的方案,而采用中密度准循环奇偶校验(Quasi-Cyclic Moderate-Density Parity-Check,QC-MDPC)码来代替原始Goppa 码所构造出的变型方案是有希望达到密钥量与安全性相对平衡的优良方案。1962 年,Gallager[4]提出了低密度奇偶校验(Low-Density Parity-Check,LDPC)码,它是一类具有稀疏校验矩阵的线性分组码,译码复杂度低。2000年,Monico等[5]利用LDPC 码来代替Goppa码,构造了新的McEliece 公钥密码方案。2007 年,Baldi 等[6]将低密度准循环奇偶校验(Quasi-Cyclic Low-Density Parity-Check,QC-LDPC)码应用于McEliece 公钥密码方案中。但上述这些方案不久便被证明是不安全的,易受到译码攻击和结构攻击。2013 年,Misoczki等[7]在前人工作的启发下,提出了基于中密度准循环奇偶校验码的McEliece 公钥密码方案。该方案已被证明能抵抗QCLDPC码公钥方案所受到的相关攻击,在保证一定安全性的同时具有较小的密钥量。但在2016 年,Guo 等[8]提出了针对该方案的一种反应攻击:密钥恢复攻击(key recovery attack),简称GJS(Guo,Johansson and Stankovski)攻击。在最近NIST 所征集的相关QC-MDPC 码的公钥方案中,能否抵抗GJS 攻击已成为判断方案好坏的一项基本准则。因此,找寻更多更好的方法来解决现有面临的GJS 攻击,是研究关于QC-MDPC 码公钥密码方案的一个重要方向。
将喷泉码级联到QC-MDPC 码公钥密码方案中便是本文对于抵抗GJS 攻击的设想。1998 年,Byers 等[9]首次提出了数字喷泉(Digital Fountain)的概念,但并没有给出现实可行的方案。2002 年,Luby[10]提出了一种可实际应用的喷泉码,被称为LT 码。2006年,Shokrollahi[11]在LT 码的基础上继续提出了新的喷泉码,被称为Raptor 码。Raptor 码实际上是LT 码和分组码的级联码,因此本文采用LT 码和QC-MDPC 码级联来构成一种类Raptor码,是具有一定可行性的。目前,数字喷泉码技术常应用于无线多媒体广播和分布式存储等领域,将喷泉码结合到公钥密码学中是其应用前景的一个新构想,因此喷泉码作为一种前向纠错技术在信息安全方面的研究是值得深入探讨的。
1 相关工作
1.1 QC-MDPC码McEliece公钥方案
中密度准循环奇偶校验(QC-MDPC)码中,中密度是指该码的奇偶校验矩阵的行重量相较于LDPC 码略高;准循环是指该码的奇偶校验矩阵的每行可由第一行循环移位不同数量的码字得到;奇偶校验是指该码是由其奇偶校验矩阵所表示的。LDPC 码的校验矩阵行重量一般不大于10,而中密度奇偶校验(Moderate Density Parity Check,MDPC)码的校验矩阵行重量为O()的数量级。由于QC-MDPC码的校验矩阵使用了准循环结构,生成该矩阵的第一行便能得到校验矩阵,因此在实际中只需存储第一行码长,提升了存储空间的利用率。如图1 所示是一个(56,32,14)-QC-MDPC 码的校验矩阵H。

图1 QC-MDPC码的校验矩阵HFig.1 Check matrix H of QC-MDPC code
QC-MDPC 码一般由四个参数表示,即(n,k,w,t)-QCMDPC 码。其中,n表示码长;k表示码的维度;w表示校验矩阵固定行重量;t表示码的纠错能力。除此之外,n还表示校验矩阵的列数,r(r=n-k)表示校验矩阵的行数,被称为余维度,且n=n0r。如表1 所示为现已提出的多个安全级别下QC-MDPC码的相关参数[7],其中n0=2。

表1 不同安全级别下的QC-MDPC码参数Tab.1 Parameters of QC-MDPC code under different security levels
基于QC-MDPC 码的McEliece 公钥密码方案由三部分组成:
1)密钥生成。
生成一个能纠t个错误的(n,k,w)-QC-MDPC 码的校验矩阵H,H∈;根据校验矩阵H来转换得到生成矩阵G,G∈;将校验矩阵H作为私钥,生成矩阵G作为公钥。
2)加密。
给定一个明文m∈,一个重量w(e) ≤t的噪声变量e∈,密文通过计算得到:c←mG+e。
3)解密。
令φH是能纠t个错误的MDPC 码译码算法,则明文通过计算得到:mG←φH(mG+e),最后从mG前k个位置中提取明文m。
在密钥生成中,校验矩阵H是通过不断循环位移得到。首先生成一个二进制字符串h0,来作为分块矩阵的第一行;然后进行循环位移生成其他行来得到分块矩阵H0;最后将分块矩阵H0整体循环位移从而最终得到校验矩阵H。生成矩阵G是通过分组码中校验矩阵与生成矩阵的关系转换得到。关于解密中的译码算法,Gallager[4]最初提出了硬判决和软判决两类算法。硬判决算法称为比特翻转(Bit Flipping,BF)算法。软判决算法又叫作概率解码算法,目前来说性能最佳的概率解码算法为置信传播(Belief Propagation,BP)算法。根据研究现状,QC-MDPC 码的译码一般采用Misoczki 等[7]所改进的BF 算法。BF 算法的基本思想为:当译码接收到一个比特时,计算对应的校验子(syndrome),并统计奇偶校验方程(unsatisfied parity-check equations)不成立的总数,记为counter,若计数值counter超过阈值T(threshold),则翻转该比特。比特翻转后的码字继续重复上述过程,经过一定的迭代轮次后,当校验子的值为0 或迭代次数达到上限,则译码完成。
1.2 数字喷泉码
数字喷泉码是差错控制中的一种前向纠错编码(Forward Error Correction,FEC)技术,即能在删除信道中进行码字纠删。在通信传输时,信道难免会发生丢包或误码,因此在删除信道中,接收端要么接收正确信息,要么接收错误信息对其丢弃。解决这一问题的一种方法可以是采用反馈重发(Automatic Repeat-reQuest,ARQ)技术[12],即当接收端收到错误信息后,便对发送端进行反馈要求重发消息。ARQ 的技术原理相当简单直观,但其缺陷也较为明显。当传输数据较大时,即使在一定误码率下,接收端进行的反馈重发量也会很大,这样便增加了通信的负担,也影响了传输效率,同时ARQ技术下的通信信道利用率并不高,会引起信道资源的浪费。因此,将ARQ 替换为对消息进行编码来达到纠错的目的,这便是信道编码的优势。
LT 码和Raptor 码是喷泉码中两种典型码型。LT 码性能的好坏主要取决于度分布函数,其编码步骤[10]如下:
1)将需要被发送的数据进行等长l分组得到n个数据包;
2)根据设计好的度分布函数f来随机获得一个度数δ;
3)在n个数据包中随机选取δ个并对其全部进行异或运算来得到一个编码包;
4)重复上述步骤来获得足够多的编码包。
上述过程如图2 所示。从该过程可以看出,为保证后续译码,生成的编码包数量不少于n,且理论上生成的编码包个数是不受限的。这也体现了喷泉码的“无码率性”,即在编码过程中获得的编码包数量不固定,因此码率就不固定,如同喷泉一样源源不断地向接收端传输。对于LT码的编译码过程,实际上可看作为类似分组码的矩阵变换:将分组的n个数据包记为P=(p1,p2,…,pn),获得的编码包记为B=(b1,b2,…,bn)。那么由矩阵P变换到矩阵B的过程可表示为:B=P⋅F,同时译码过程即可表示为:P=B⋅F-1,其中F称为编码矩阵,F-1为编码矩阵的求逆过程。显然,编码矩阵F的结构和度分布函数f密切相关,为了使译码复杂度较小,因此需要对度分布函数f精心设计。编码矩阵的求逆过程,即译码可采用高斯消除算法或置信传播算法来恢复数据,高斯消除算法有更优的译码性能,置信传播算法运算复杂度相对较低,根据综合考虑,实际常采用置信传播算法对LT 码进行译码。
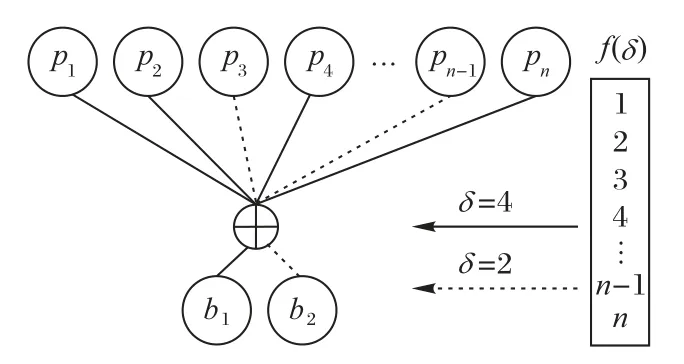
图2 LT码编码示意图Fig.2 Schematic diagram of LT code encoding
Raptor 码是在LT 码的基础上发展而来的。由于LT 码在编码过程中选择数据包进行异或操作具有随机性,可能存在某个数据包从未被进行编码,则接收端无法获取该原始数据而导致译码失败。因此在LT 编码过程中会刻意选取较大度数来进行一定量的编码,从而保证原始数据被完全覆盖。但这样会带来过多的编译码过程中的异或操作,减小了译码过程中可译集的大小,使得译码仍存在一定的失败率。Raptor的设计很好地解决了上述问题。Raptor 是将分组码和LT 码进行级联编码得到,先使用分组码对原始消息进行预编码,然后使用LT 码进行编码得到编码包进行发送[11],如图3 所示为Raptor 码编码过程。使用级联编码的好处在于对Raptor 码进行译码时,若出现对LT 码的译码失败,那么可以利用分组码的自纠能力继续译码来消除失败。因此,Raptor 码中的LT 码无须产生太多高连接度的编码包,这样既保证了数据被良好覆盖,同时又具有较高的译码成功率和较低的编译码复杂度。
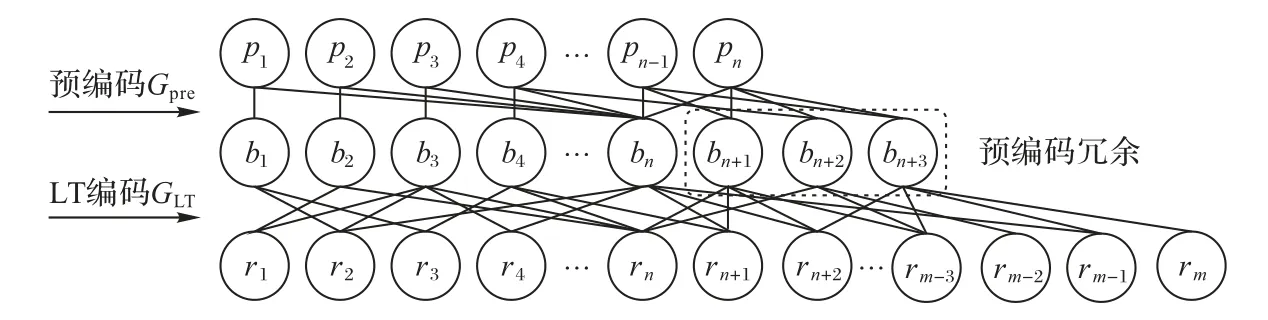
图3 Raptor码编码示意图Fig.3 Schematic diagram of Raptor code encoding
2 密钥恢复攻击
2016 年,Guo 等[8]提出了一种对QC-MDPC 码下的McEliece 公钥密码方案的攻击:密钥恢复攻击,简称GJS 攻击。其通过对接收机解密是否成功这一反应,判断并获得私钥的相关信息,从而来恢复方案的私钥。
2.1 攻击情景
假设Alice 为发送方,Bob 为接收方,Eve 为攻击者。Alice首先利用QC-MDPC 码McEliece 公钥方案的公钥对消息m加密生成密文c进行发送,Bob 接收到密文c后使用对应私钥解密。若解密成功,则Bob 对Alice 回复确认或不作回复;若解密失败,则Bob 对Alice 反馈要求重发消息。Eve 作为敌手,同样对消息m使用公钥加密生成密文c,但会选择一种特定的错误图样e与密文c进行异或运算,得到密文ce进行发送。同样Bob 接收后使用私钥解密,当解密失败后Bob 要求重发消息时,Eve 能截取到此反馈,经过大量消息的传输后,Eve 便能统计获得相应的译码失败率。Eve 通过分析大量实验下的译码失败率和私钥结构的关系后,最终恢复出私钥。
2.2 攻击原理
Eve发送的密文ce=mG+e被Bob接收后,根据比特翻转算法的步骤,开始计算校验子s=ceHT=mGHT+eHT=eHT,该结果表示计算校验子实际上只和错误图样e有关,则对于第j位的奇偶校验方程为:sj=。若sj≠0,那校验方程不成立的个数增加一个,当计数(counter)达到一定值,即超过阈值时,那么密文c对应的第i位置的比特将会翻转。因此,对于敌手设计的错误图样e,它会影响译码时变量节点是否发生比特翻转的情况。同时,BF 是一种迭代算法,在一定的迭代次数下,若未正确地完成所有比特翻转,那么译码失败。所以,敌手可以通过多次的实验来获取译码失败情况,找寻错误图样e和译码失败的关系,这一关系表述为:若错误图样e中两位1 之间的汉明距离也存在于校验矩阵H的第一行向量h0的两位1 之间,那么此时译码失败率要比不存在情况时的小。根据该关系,敌手通过译码失败的统计数据来得到向量h0中存在的汉明距离和重数,即距离谱D。利用距离谱进行深度优先搜索恢复出向量h0,最后进行线性变换恢复出校验矩阵H,即破解出私钥。
2.3 攻击结果
文献[8]给出了在选择明文攻击(Chosen Plaintext Attack,CPA)和适应性选择密文攻击(Adaptive Chosen Ciphertext Attack,CCA2)两种攻击等级安全下实施GJS 攻击的结果。在80-bit安全下,CPA 情景的参数如下:当t=84时,M=105,U=2400;当t=90 时,M=104,U=2400。其中,M为某特定错误图样e下一次实验加解密传输的消息量,U为选择不同错误图样e所进行的实验次数。在M×U的消息传输量下,GJS 攻击能成功恢复私钥。对于CCA2 情景,当t=84时,至少需要M×U=2.03× 108的消息传输量来恢复出私钥,而最差情况下则需要M×U=3.56 × 108。由于CCA2 的安全级别更高,因此需要的代价较CPA 情景下更大,因此实验所需的消息传输量更多。
3 类Raptor码级联QC-MDPC码公钥方案
密钥恢复攻击的特点在于它是一类反应攻击,即攻击者利用接收端译码失败时的反应来恢复出私钥,因此通信传输中反馈信道是进行密钥恢复攻击的必要条件。若对反馈信道进行加密处理或直接用其他方式代替反馈信道,那密钥恢复攻击的实施复杂度将会极大增加。喷泉码便是十分契合抵抗密钥恢复攻击的设计,在基于QC-MDPC 码的McEliece 公钥方案中级联LT 码,得到一种类Raptor 码的公钥方案。在该方案下当译码失败时,接收端无须反馈重发,而是继续接收源源不断的编码包直到译码成功。本文提出的类Raptor 码级联QCMDPC码的公钥方案由密钥生成、加密和解密三个部分组成。
3.1 密钥生成
根据QC-MDPC 码和LT 码的级联过程,首先生成QCMDPC码的McEliece公钥方案中的公钥:生成矩阵G,私钥:校验矩阵H。然后通过LT码的编码过程来获得编码矩阵F。最后将G'=GF作为方案的公钥,将H和F(F-1)作为方案的私钥。其中
3.2 加密
对明文m∈使用公钥进行级联码加密:mG'。然后考虑信道中加入的错误图样e,其重量不大于整个级联码的纠错能力,得到最终的密文c=mG'+e。
3.3 解密
解密为加密的逆过程,先对密文c进行级联过程中LT 码的译码:mG=φF-1(mG'+e),其中φF-1表示为置信传播算法。然后进行对QC-MDPC码的译码:m=φH(mG),其中φH表示为比特翻转算法。最终解密获得明文m。
4 参数与效率分析
4.1 参数分析
根据方案描述,在级联码中,QC-MDPC 码需考虑的是相关参数(n,k,w,t),方案仍采用QC-MDPC码McEliece公钥密码方案。LT 码需考虑编码矩阵F所对应度分布函数f中的相关参数x和δ,其中:x表示生成的编码包个数,即编码分组数;δ表示度数。而编码包长参数l,由于其不会影响LT 码译码性能,为了方便分析,方案确定l=1。对于设计优良的LT码,需要尽可能生成少的编码分组来保证译码开销较小,同时还需要尽量小的编码符号平均度数来保证编译码代价较小。这两点也符合了本文方案的设计要求:较少的编码分组数意味着较小的密钥量以便存储,较小的编码符号平均度数意味着方案运行效率相对更高。
在LT 码中,译码开销用参数ε表示,是指当输入符号数为n时,接收到的编码分组数为x且能以高概率1-γ成功译出这n个符号,那么x=(1+ε)n,即ε=-1。编译码代价是指生成编码包和恢复原始数据的编译码操作数,即编译码复杂度。文献[10]中给出了度分布函数的几种选择,如表2所示。

表2 三种度分布函数的比较Tab.2 Comparison of three degree distribution functions
文献[10]分析了这三种度分布函数并得出采用鲁棒孤子分布是最优选择的结论。从编码分组数可以看出,鲁棒孤子分布所需要的译码开销相较于度一分布要小很多,但无法达到理想孤子分布的最优情况。不过鲁棒孤子分布改善了理想孤子分布存在的问题:可译的度数为1 的编码包不够多会容易导致译码失败。从平均度数上看,鲁棒孤子分布需要的编译码操作数大致接近理想孤子分布。综合考虑,鲁棒孤子分布的性能最佳。根据具体的信道特点,新的度分布函数也被研究者们不断提出,但本文方案暂不考虑度分布的设计,选择鲁棒孤子分布作为LT码分布函数已达到方案的安全要求。
上述单从LT码分析了其译码开销,但对于本文方案级联码的译码开销来说,ε并不确定。由于QC-MDPC 码具有一定的自纠能力,因此LT码在译码时未完全译出也可能最终解密成功,此时εR≤εLT。同时使用BF对QC-MDPC 译码时可能会出现失败,则此时εR>εLT。而级联码的译码开销决定了编码分组数x的取值。最优情形为x=n时,消息便能成功译出;最坏情形为x=(1+εm)n,其中εm表示对任意消息都能以1的概率成功解密时的译码开销。因此方案在确定编码矩阵F的大小时,x的取值应考虑最坏情形,即x=(1+εm)n。
4.2 密钥量和复杂度分析
本文方案的公钥为G'=GF。矩阵G'的大小为k×x,即公钥密钥量为(n-r)x比特。而在QC-MDPC 码的原始方案中,矩阵G为准循环结构且可化为系统矩阵,其密钥量为(n0-1)r比特。本文方案由于对矩阵G右乘了矩阵F,公钥的准循环结构被认作消失,因此两者对比密钥量相差了x倍。本文方案的私钥为H和F(F-1)。矩阵H同为准循环结构,其密钥量为n0r比特。而矩阵F(F-1)更多是作为一种私钥形式,表现为LT码的译码算法,因此实际中无须对其进行存储。
方案的复杂度围绕密钥生成、加解密过程分析。在密钥生成阶段,矩阵G和F相乘获得G'需要(2n-1)kx次比特操作,该复杂度大于QC-MDPC 码方案下生成公钥G时的复杂度,但仍小于QC-LDPC 码方案下生成公钥G2=S-1GQ-1时的复杂度。在加密阶段,明文m与公钥G'进行矩阵相乘运算,需要(2k-1)x次比特操作。在解密阶段,对LT 码和QCMDPC 码的解码分别采用置信传播算法和比特翻转算法。BP译码算法复杂度为O(nlnn),而LT 码的另一译码算法高斯消除算法复杂度为O(xn2),两种算法相较BP 复杂度更适合本文方案。BF译码算法复杂度为O(nwI),I为迭代次数。
5 抵抗GJS攻击
基于纠错码的公钥密码方案一直以来面临着两类攻击的安全挑战:译码攻击和结构攻击。译码攻击是直接破解得到明文,结构攻击则是破解方案的私钥。Misoczki等[7]提出的基于QC-MDPC 码的McEliece 公钥密码方案已被证明能抵抗消息集译码攻击(Information Set Decoding Attack),在80-bit安全下,攻击实现的复杂度为O(281.04),因此可以达到该比特安全性。同时该方案还能抵抗找寻原码对偶码的低重量码字的结构攻击[13]。但Guo 等[8]提出了一种新的结构攻击——GJS 攻击,是目前对于QC-MDPC 码公钥方案最具威胁的攻击之一,本文提出的级联码公钥方案能有效抗击GJS 攻击。根据Raptor 码的实现流程来得到方案的具体实现,并考虑GJS 攻击在此情景下的影响进而分析抗击效果。
5.1 Raptor码系统流程
基于Raptor 码的编译码系统流程如图4 所示。从图4 中可以看出,此过程中存在反馈系统,同时结合了喷泉码具有的FEC 机制,使得整体上采用了混合自动重传请求(Hybrid Automatic Repeat-reQuest,HARQ)[14]技术。接收端在对一次消息成功译码后,会向对方反馈一个确认信息(ACKnowledge,ACK),让其停止发送编码包;当译码失败时,接收端不会作任何反馈,而是等待对方发送更多的编码包直至译码成功。可以看出整个过程对译码失败的相关信息具有一定的隐藏能力。
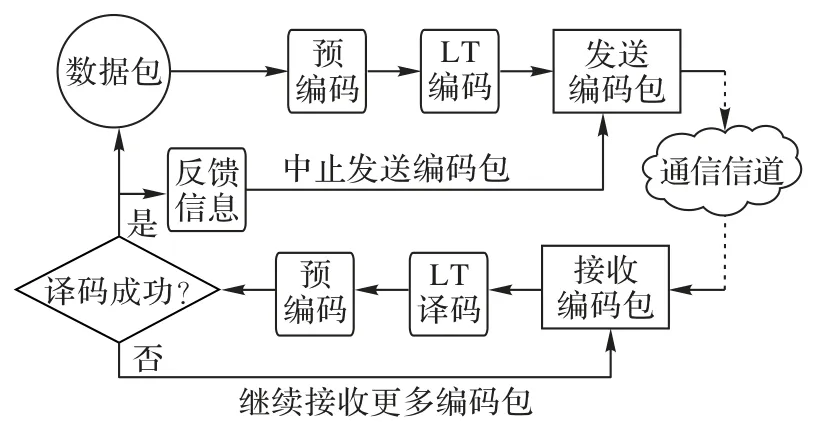
图4 Raptor码的编译码系统流程Fig.4 Flow chart of Raptor code encoding/decoding system
但本文方案无法直接采用上述系统,因为不能达到完全匹配,同时还存在一些缺陷:由于HARQ 机制的存在,那么发接收端需要进行一定的同步,即通过接收端的反馈来控制发送LT 码编码时编码包的量。而本文方案是直接由矩阵运算完成级联码加密,采用上述动态过程是不现实的。除此之外,过程中的反馈系统仍是一个安全隐患。虽然为正向反馈,但攻击者仍可能利用该反馈系统进行攻击,如利用旁道攻击(Side-Channel Attack)中的计时攻击(Timing Attack)。文献[15]提出了一种在GJS 攻击上改进的计时攻击,若攻击者能获取QC-MDPC 码进行BF 译码时的迭代次数,那么攻击者同样能得到私钥H的距离谱和迭代次数的关系图,并通过大量样本实验来恢复出私钥H。而迭代次数实际上是通过译码运行时间来体现的,所以何时收到反馈信息便是攻击者计算译码时长的途径,从而有可能对本文方案实施类似的计时攻击。因此,本文方案的实现情景需要在Raptor 码的编译码系统流程的基础上进行修改。
5.2 方案情景与抗击效果
本文方案的实现情景如图5 所示。该情景删除了Raptor码系统流程中的反馈系统,同样能达到抵抗GJS 攻击的效果。其分析如下:
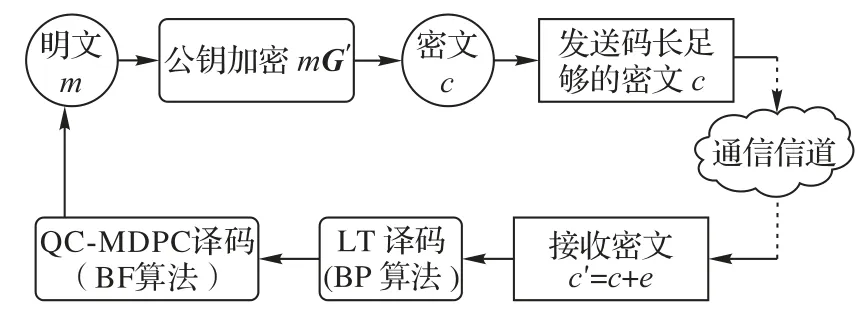
图5 本文方案实现流程Fig.5 Realization flow chart of proposed scheme
当敌手准备GJS 攻击时,首先对消息进行本文方案的级联编码,即使用公钥G'对消息加密。然后选择特定错误图样e,得到密文c∈。公钥G'对于原始方案的公钥G来说,只是矩阵略大一些,面对敌手其在形式上是一样的,因此敌手对特定错误图样e仍按照原方法构造且e∈。
GJS 攻击的本质是利用特定错误图样e来影响BF 译码效果,通过大量实验结果来反映出距离谱D信息从而恢复出私钥H。因此在原方案中生成mG+e是GJS 攻击成功的前提,但本文方案由于加入了LT 码的编码,所以生成的是mGF+e,编码矩阵F将mG隐藏起来,此时e主要影响的是F,这意味着错误图样只是改变了LT 码编码时度数δ的大小,即数据的连接度情况。当方案的参数x足够大,即译码开销具有合适大小时,便能生成足够多的编码包来保证LT 码在BP译码时都能成功译出消息,因此在本文方案下GJS 攻击生成的错误图样e无法影响QC-MDPC码的译码结果。
除此之外,方案将F作为了私钥,因此敌手很难通过G'恢复出G,进一步加大了攻击难度。同时方案还考虑了译码时的最坏情况,保证加解密过程中始终能译码成功,因此便无须反馈系统,从根本上阻止了反应攻击。综上分析,本文方案在抵抗GJS攻击上是十分有效的。
5.3 仿真分析
本文分析了GJS 攻击的内在过程,并提出了相应理论上的应对措施。对于本文方案能否抵抗GJS 攻击的关键在于确定合适的译码开销值大小。根据本文方案在GJS 攻击下的情景,可对参数选择合适数值后进行模拟仿真。随机选取待加密明文m,其长度为480比特,QC-MDPC码长n为960比特,码率为0.5。LT 码的度分布函数采用鲁棒孤子分布,其参数为α=0.03,γ=0.5。信道错误图样e引起的删除概率为0.1。对一次消息加解密实验重复进行1000次,最终获得方案级联码的性能如图6所示。

图6 方案译码开销与译码成功率关系Fig.6 Relation between decoding overhead and decoding success rate
由图6 中仿真结果可以看出,私钥F需确定的参数x=(1+εm)n≈1.65n。为了方便模拟,QC-MDPC码选择的参数为原方案参数大小的1/10。而在LT 码的译码时,其码长会影响译码效果,即码长越长,译码效果在低冗余时提升越明显[16]。因此实际中若使用QC-MDPC 码原方案,译码开销εm或将会低于0.65。不过值得注意的是,上述仿真理想化了QC-MDPC码的译码,未考虑其存在一定译码失败的情况。那么综合分析得出,εm至少为0.65来保证最坏情况时的译码成功。
确定了较好数值大小的译码开销εm后,对于方案在实际应用中,可以保证存储中的密钥量不会过大。而在安全性上,由于实际因素复杂,理想情况中的译码百分之百成功难以达到。但根据抵抗GJS 攻击中比特安全性定义:对于a-bit 安全级别,若方案的译码失败率小于2-a,那么方案能抵抗相关攻击。因此方案在较小译码失败率下仍可保持应用中抵抗GJS攻击的效果,所以选择了优良数值的译码开销εm后,便保证了译码失败率可以忽略。
6 不同方案的对比分析
本文提出的基于QC-MDPC 码级联码的公钥密码方案能有效抵抗GJS 攻击,对本文方案与已有的能抵抗GJS 攻击的方案进行了比较。
6.1 本文方案的公钥密钥量
根据上述分析可知本文方案的公钥密钥量为(n-r)x,其略大于MDPC 码生成矩阵G参数(n-r)r。但MDPC 码是不具有公钥设计价值的:根据MDPC 码与其他码型方案的比较,若将MDPC 码的生成矩阵作为公钥,其密钥量甚至大于原始的McEliece 方案的公钥量。密钥量这么大的原因在于MDPC码不存在准循环(Quasi-Cyclic,QC)结构,因此需存储整个矩阵而不是矩阵中的某一行。本文方案同样面临这样的问题,若要让方案的公钥密钥量减少,那么需要保证公钥G'具有一定的循环结构。由于G'=GF,其中G可化为系统形式并具有准循环结构,那么F便是保证G'循环性的决定因素。因此,如何改良设计LT码编码时的度分布函数f就成为了本文方案的改进目标。
关于对矩阵F的考虑,最直观的是使其成为准循环结构,但这样可能会导致一定的安全问题,这点下文将会分析。不过可以降低对G'的循环性要求,即无须达到准循环,而让G'的每行或列之间存在某种规律,同样也能达到减少密钥量的效果。除此之外,根据文献[17]提出的相关方案,表明存在非准循环结构的F也能保证G'的准循环性,而满足这种条件的F有多少个也是今后需要进一步验证的。
6.2 本文方案的抗攻击性能
本文主要分析了所提出的公钥密码方案对GJS 攻击的抗击效果,需要对QC-LDPC/MDPC 码易遭受的其他攻击进行讨论,来综合分析方案的安全性能。
消息集译码攻击[13]是利用公钥G和错误图样e来构造出一个可逆矩阵G1从而恢复明文,即m=cG1-1=(mG+e)G1-1=mGG-1+ee-1。而消息集译码算法如Stern 算法和MMT(May,Meurer and Thomae)算法[18],其时间复杂度都是指数级别的,约为O(20.05n),本文方案和原始QC-MDPC 码的公钥密码方案在参数n上相同,即80-bit 安全级别下攻击复杂度约为O(2480)。显然本文方案是能抵抗此攻击的。
搜寻公钥对偶码的低重量码字的结构攻击[13],是利用QC-LDPC 码的McEliece 公钥密码方案的私钥H进行实施的,其基本原理是针对私钥H的稀疏性特点,即行重量太小进行攻击。而本文方案仍以QC-MDPC 码为基础,则私钥H的密度足够大,因此能抵抗此攻击。
2010 年,OTD(Otmani,Tillich and Dallot)攻击[19]是针对公钥形式为G2=S-1GQ-1的QC-LDPC 码的McEliece 变型方案而进行实施的,其中,S和Q分别为非奇异加扰矩阵和非奇异变换矩阵且都稀疏。本文方案的公钥G'=GF与上述条件明显不符,因此该攻击对本文方案无效。
一种寻找弱密钥的密钥恢复攻击[20],其攻击点为原始的QC-MDPC 码McEliece 公钥密码方案,即利用公钥G来恢复私钥H。本文方案将G进行了隐藏同时还存在其他矩阵作为私钥,因此该攻击不可行。
FHP(Fabšič,Hromada and Paul stankovski)攻击[21]是一种对本文方案安全性有威胁的反应攻击,与GJS 攻击十分相似。其攻击点为QC-LDPC 码McEliece 公钥密码方案,即利用公钥G2=S-1GQ-1且构造特定的错误图样e来观测译码结果。在此情景下,加密为c=mS-1GQ-1+e,解密先对c右乘Q得到c'=mS-1G+eQ,最后利用译码算法纠错eQ得到mS-1并恢复出明文m=mS-1S。由此看出,影响译码结果的为eQ,所以FHP攻击便会利用Q的循环且低密度特性来获取距离谱与译码结果的联系,从而恢复私钥。本文方案的公钥形式也存在对G右乘矩阵F,根据上述密钥量的分析,F若为循环结构虽有利于公钥存储,但这样也有可能利于FHP 攻击的实施。不过本文方案在解密时为级联码的分步译码,在LT码译码时很大程度上消除了错误图样,并且方案删去了反馈系统,所以在理论上是能抵抗FHP攻击的。
6.3 各类抵抗GJS攻击方案对比
一些代表性研究根据GJS 攻击的特点也提出了抗击方案。本文方案与这些方案的特性对比如表3 所示,各方案的具体介绍如下。

表3 不同抵抗GJS攻击方案的特性比较Tab.3 Characteristic comparison of different schemes against GJS attack
Eaton等[15]提出了使用“静态密钥”进行密钥封装的方案:ParQ 加密方案(Parallelized QC-MDPC KEM)。该方案的抗击原理为:首先生成QC-MDPC 码的McElicec 方案的公钥G和私钥H,令par为平行数,取值范围为3~12。然后将公钥G通过ParQ 加密算法来获得par个平行公钥,利用平行公钥对明文进行加密得到封装密文C=(c1,c2,…,cP-1,cP)。最后通过ParQ 解密算法对封装密文C解密,即通过私钥H来对密文c解密,当且仅当P个密文c译码失败时,才记作ParQ 解密失败,否则解密成功。根据该方案的描述,可以看出其原理与本文方案十分相似,都是对原McEliece 方案的公私钥进行改造来降低译码成功率,使其达到能抵抗GJS 攻击的安全标准。而改造后的公私钥相对更大,因此在某种程度上是通过密钥量来换取方案的安全性。
Barreto 等[22]提出了CAKE(Code-based Algorithm for Key Encapsulation)。该算法的抗击原理为:方案采用临时密钥,即动态密钥,进行密钥封装,当完成一次明文的加解密后,使用过的“密钥对”便会更新。由于每次解密所使用的私钥是不断变化的,因此恢复私钥便没有意义,GJS 攻击便完全失效。不过CAKE 并非McEliece 型,而是基于ElGamal 型的公钥密码。其特点表现为:算法将私钥矩阵乘以随机循环密度矩阵来隐藏私钥的结构,其不同于McEliece 型对私钥右乘公钥来隐藏私钥结构的特点。在NIST 所征集的一类基于编码的密码方案即BIKE(BIt flipping Key Encapsulation)方案[23]中,第一种算法BIKE-1 为CAKE 的改进,并在最新的BIKE 方案中,提升了译码算法的性能,获得了更优的译码器即Backflip Decoder[24]。该译码器可以让方案在静态密钥下,使译码失败率足以忽略,从而实现更高的安全性。
7 结语
本文提出了一种类Raptor 码的级联码公钥密码方案,该方案是QC-MDPC 码McEliece 公钥密码方案基础上的改进。分析结果表明,通过牺牲原方案在密钥量和加解密复杂度上的一些优势,本文方案获得了在安全性上的提升,其表现为能抵抗GJS 攻击等一些反应攻击和其他相关攻击。但本文方案也存在一定的缺陷,如密钥量的问题。同时方案还存在一些改进的方向,如对级联码能否提出更优的整体译码方案来提升译码效率。这些都是未来需要进一步研究的方向。

