基于三轴重型全驱电动汽车路面附着系数估计
路永婕,韩寅锋,王翠艳,张俊宁,马智喆
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.石家庄铁道大学 机械工程学院,河北 石家庄 050043)
路面附着系数估计是实现车辆主动安全技术的关键因素之一,目前国内外对汽车路面附着系数估计的研究已有很多。熊璐等[1]分别构建了纵向力观测器和侧向力观测器对纵侧2方向的路面附着系数进行估计,又根据模糊逻辑设计了融合估计算法,实现了对复杂路况下的路面附着系数估计;王震坡等[2]将无迹卡尔曼滤波与模糊理论相结合,提高了算法的鲁棒性和自适应性;林棻等[3]将神经网络应用到参数估计中,以相关动力学参数作为输入,通过学习、训练,实现估计效果的提升;赵立军等[4]推导了利用附着系数和峰值附着系数之间的递推公式,利用递推最小二乘法估计峰值附着系数;王博等[5]提出了7种典型路面的特征因子阈值及其区间进行路面识别;Ma et al[6]针对汽车转向工况,通过提出基于单轮前轴调心扭矩来估计路面附着系数;Sun et al[7]提出一种基于遗忘因子的卡尔曼滤波的改进算法,通过估计u-s曲线的斜率得到路面附着系数估计值。
由上述可知,路面附着系数估计的研究多针对于四轮汽车的研究,对于重型三轴电动汽车研究较少。重型三轴汽车多用于长距离运输货物,且操作难度比常规四轮汽车大,更容易发生重大交通事故;其在结构、运动特性以及动力特性方面都要比四轮汽车更加复杂[8],特别是重型三轴电动汽车前轴与中后轴距离较远,前后车体所处路面可能会有较大差别,故重型三轴电动汽车在路面附着系数估计方面存在着与四轮汽车不同的特性和问题。综上,针对重型三轴电动汽车建立9自由度整车模型,包括纵向、横向、横摆车轮转动;采用UKF滤波算法对6个车轮的路面附着系数分别进行估计,并通过Matlab/Simulink进行仿真分析,取得准确的估计结果,为之后重型三轴电动汽车的状态估计奠定了基础。
1 建立9自由度整车动力学模型
1.1 整车3自由度模型
如图1所示,以东风某三轴重型汽车为参照,建立3自由度六轮整车模型,包括:纵向、横向、横摆3个方向的运动。对所有影响因素进行分析,做出如下假设:固定在汽车上的坐标系原点与三轴重型汽车的质心重合;忽略汽车悬架的作用和垂直方向的运动;该车无绕Y轴的俯仰运动和绕X轴的侧倾运动;汽车各轮胎的机械特性相同;为简化问题,线性化方向盘转角和前轮转角关系。

图1 整车3自由度模型
动力学方程[9]
may=Fxfrsinδfr+Fyfrcosδfr+Fxflsinδfl+Fyflcosδfl+Fymr+Fyml+Fyrr+Fyrl
(1)
max=Fxfrcosδfr+Fyfrsinδfr+Fxflcosδfl+Fyflsinδfl+Fxmr+Fxml+Fxrr+Fxrl
(2)
(3)
考虑纵向和侧向加速度的影响,各轮胎的垂直载荷可表示为
(4)
式中的参数如表1所示。

表1 车辆参数表
1.2 Dugoff轮胎模型
Dugoff轮胎模型[10]
(5)
式中,μ为轮胎与路面的附着系数;Cx、Cy分别为轮胎纵滑及侧偏刚度;ε为速度影响因子。为方便估计路面附着系数,将Dugoff轮胎模型简化为下述归一化模型,即可写为
(6)

1.3 9自由度整车仿真模型
根据上述模型,基于Matlab/SimulinkR2018b软件来实现整车模型的搭建和仿真。考虑到对路面附着系数估计所需的车辆动力学响应,建立了纵、侧、横摆以及六轮转动9自由度非线性车辆模型[11-15],其原理如图2所示。
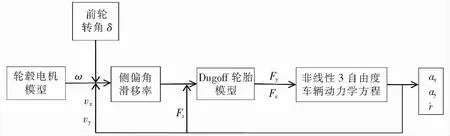
图2 非线性车辆模型原理图
2 UKF估计算法
无迹卡尔曼滤波算法[16-17]的整个过程为:①通过比例无迹变换得到采样点;②一步预测;③量测更新;④迭代运算。
UKF过程中的初值,测量噪声协方差R=0.05I3×3,过程噪声协方差P=0.019I6×6,初始误差协方差P0=0.01I6×6。
根据式(1)~式(3),分别建立状态方程(7)和量测方程(8)。
(7)
(8)
式中,随机变量w(t)和v(t)分别为过程噪声和测量噪声。
(9)
3 路面附着系数估计结果分析
3.1 匀速直行工况
分别设置路面附着系数为0.8、0.3、对开路面(左侧路面0.8,右侧路面0.3),分别进行60 km/h的匀速直线行驶,以左侧车轮为例(对开路面为全部车轮),路面附着系数估计结果如图3所示。
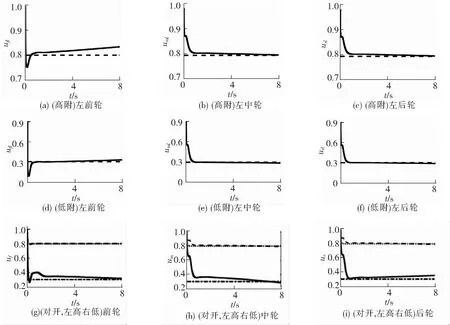
图3 匀速直行工况下路面附着系数估计结果
从图3(a)~图3(c)可以看出,车轮与路面之间的附着系数估计值均在0.9 s之前收敛到0.8,高附路面下左前轮算法收敛值偏移最大为0.04,这是估计过程中不可避免的波动,估计结果仍然在[0,0.05]误差范围内收敛,其中图3(b)、图3(c)收敛效果较好,波动最大在0.02。与高附路面相比,低附路面下算法收敛更快且误差更小。从图3(g)~图3(i)可以看出,对开路面下,车辆6个车轮与路面之间的附着系数估计值均在0.8 s前收敛到实际值附近,其中,在高附路面,算法收敛更快且误差更小,相比之下,算法在低附路面估计效果波动较大且最大误差值为0.052。
3.2 角阶跃工况
给定行驶工况为80°的方向盘阶跃输入,如图4(a)所示。设置路面附着系数实际值为0.8,进行60 km/h下的角阶跃工况,以左轮为例,结果如图4(b)~图4(d)所示。

图4 角阶跃工况下的路面附着系数估计结果
由图4得,在角阶跃极限工况,车辆力学响应剧烈,重载车辆惯性较大,车辆稳定性变差,这导致算法收敛速度变慢。前轮和后轮在2.1 s 收敛至u=0.85处,中轮在1.4 s 收敛至u=0.85处。中轮的估计值在2.3 s 完全收敛至0.8,且浮动较小;后轮在4.3 s时收敛至0.8,伴有波动趋势;前轮随时间不断趋近0.8。
3.3 误差分析
根据式(10)对上述匀速直行工况和角阶跃工况下的路面附着系数估计进行误差分析,结果如图5所示。
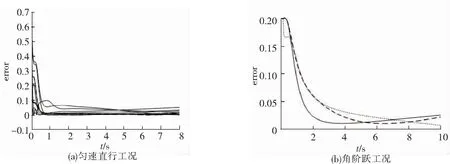
图5 误差分析

(10)
从图5可得,匀速直行工况下3种路面,12个估计结果,0.8 s之前均已收敛到误差范围[0,0.06]内,对开路面右前轮估计结果在收敛后出现大幅波动,但在1 s内恢复;角阶跃极限工况下,尽管重载车辆惯性大,极限工况下车辆力学响应剧烈,仍然在2.3 s之内将路面附着系数估计误差收敛在[0,0.05]内。
4 结论
(1)在估计精度方面,通过匀速直行工况下的高附、低附、对开路面以及角阶跃工况下的高附、低附路面的仿真实验,结果表明搭载无迹卡尔曼滤波算法的重型三轴电动汽车可以实现对其6个轮胎路面附着系数的分别估计,且估计误差在可接受范围内。
(2)在时效性方面,设计的路面附着系数估计算法在匀速直行工况下响应快,估计效果好;但在角阶跃极限工况下收敛速度慢。提高转向工况下路面附着系数估计的收敛速度将成为下一阶段的研究工作。
(3)单轮路面附着系数估计的实现意味着可以通过不同位置轮胎的路面附着系数估计情况实现对开路面、对接路面的识别,也可以对侧翻、制动失效等极端工况下的主动安全控制提供信号参考。

