基于去滑动均值趋势多重分形的上证指数分析

赖佳境 杨秋鸿

摘要：本文运用去滑动均值趋势多重分形（MFDMA）算法通过统计分析了1990-2020年的上证指数各数据，结果显示：上证各指数序列均表现出明显的右尾特征，并根据得到的Hurst指数与多重分形谱分析，上证各指数均表现出明显的多重分形特征，进一步论证证券市场存在的风险较大。

关键词：去滑动均值趋势，多重分形，上证指数，Hurst指数，多重分形谱

1.研究目的与意义

多重分形也称为多标度分形，可以用來描述具有无穷自相似层次结构系统的自相似、自仿射的特性，刻画动力学系统的长期演化和自相似行为[1]。实际生活中分形序列无处不在，对分形序列进行多重分形分析，可用于描述显示存在的许多自认现象以及社会现象，例如实际生活中的矿产预测，股市金融等[2-3]。由于证券交易系统的非线性复杂特征，将多重分形分析应用于证券交易系统，有利于推动非线性理论在证券市场的操作性应用，并为投资者提供新的渠道去认知证券交易系统的指数规律[4-5]。

因此，本文将以上海证券交易所提供的上证各指数作为时间序列，去滑动均值趋势多重分形（MFDMA）算法作为研究方法，研究上证指数序列在MFDMA算法下的Hurst指数以及多重分形谱的分形特征。

2.数据分析

2.1数据描述

我国证券市场中的上海证券综合指数，因此本文将以1990年至2020年上证指数作为研究对象，对上证指数的前收盘价、开盘价、收盘价进行描述统计，结果如表1所示。

由表1可知，上证指数的前收盘价、开盘价、收盘价均值、标准差值接近，其中开盘价的标准差最小，稳定性稍强。各指数偏度大于0，表现出右偏特征，数据序列右端有较多的极端值，数据均值右侧的离散程度强;由于各指数峰度大于0，表示数据序列与正态分布相比较为陡峭，为尖顶峰。由此可知上证各指数均不服从正态分布。

2.2上证指数的多重分形分析

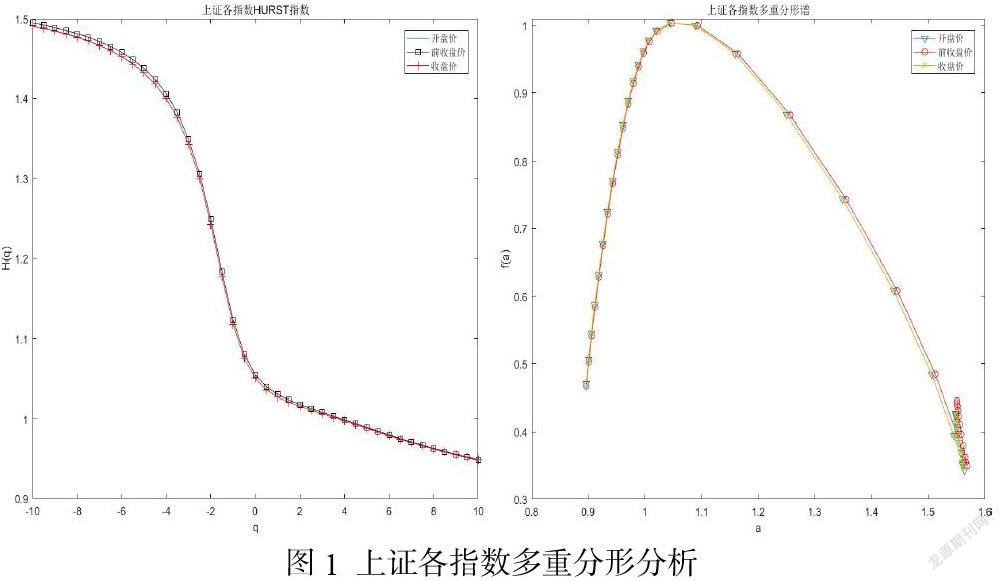
运用去滑动均值趋势多重分形（MFDMA）算法对上证指数的前收盘价、开盘价、收盘价进行实证分析，实证结果如图1所示。

由图1可知，上证指数的开盘价、前收盘价、收盘价的Hurst指数均表现出明显的非线性特征，Hurst指数H（q）随着q的增加而单调下降，表明上证各指数均有明显的多重分形特征，并且下降的幅度较为接近，其中开盘价与收盘价几乎重合，说明其多重分形特征相似度较高。另外，根据图1的上证各指数多重分形谱结果显示，三个指数均表现出明显的左钩状，而且非对称，从而说明这三个指数多重分形特征均有非对称性，多重分形特征明显。

3.结论

本文通过MFDMA算法对上海证券交易所提供的1990-2020年开盘价、前收盘价、收盘价进行多重分形特征分析，根据其Hurst指数与多重分形谱结果显示：上证各指数的多重分形特征越明显，说明交易市场存在的风险越大。而且进一步显示，MFDMA算法适用于分析上证指数存在的多重分形特征，为接下来的研究提供了一定的理论指导。

参考文献

[1]朱华， 姬翠翠. 分形理论及其应用[M]. 北京： 科学出版社， 2011： 207-221.

[2]万丽， 邓小成， 王庆飞， 等. MF-DFA方法与成矿元素分布特征---以大尹格庄金矿为例[J]. 中国矿业大学学报， 2012， 41： 133-139.

[3]Zhou W J， Dang Y G， Gu R B. Efficiency and multifractality analysis of CSI 300 based on multifractal detrending moving average[J]. Physica A， 2013， 392： 1429-1438.

[4]Kantelhardt J W， Zschiegner S K， et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physical A， 2002， 316： 87-114.

[5]熊杰，陈绍宽，韦伟，等. 基于多重分形去趋势波动分析法的交通流多重分形无标度区间自动识别方法[J]. 物理学报，2014，63：2005041-2005048.

本文为东莞理工学院城市学院青年教师发展基金《项目名称：MFDMA算法在股票市场的应用分析》项目（项目编号：2020QJY010Z）