一类非线性微分方程解的进一步研究

韦燕红，徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言与定理

本文使用Nevalinna理论的符号，假设读者熟悉值分布的相关理论（详见参考文献[1-2]）.

在复微分差分方程理论研究的众多问题中，复变量微分方程的整函数解或亚纯函数解的存在性和解的结构与性质是既重要又经典的问题，特别是非线性微分方程，这也是值分布理论的重要应用之一.大量学者运用Nevalinna值分布理论，研究了一系列非线性微分方程[3-9].

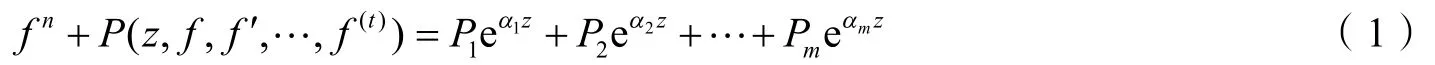
在2021年，本文作者研究了非线性微分方程

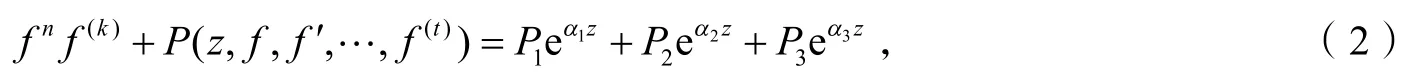
得到如下定理：

本文主要受文献[9-10]的启发，在文献[10]结果的基础上，进一步研究方程（2）右边有多个指数项时整函数解的存在性，得到了更一般性的结论：

下面给出4个例子进行说明.

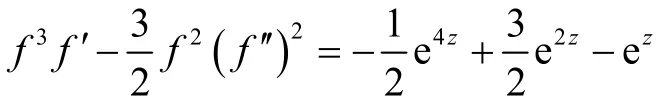
2 引理

证明定理3需要如下引理.

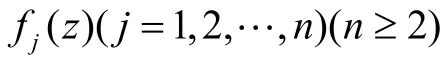
3 定理3的证明

方程（4）两边同时微分，得：

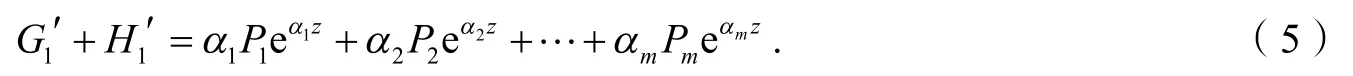
由方程（4）和（5）消去eα1z，得：

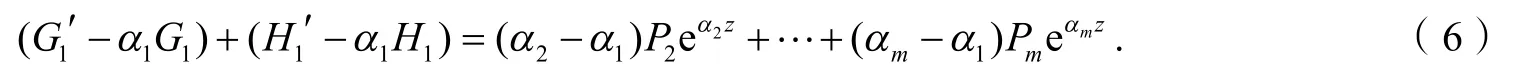
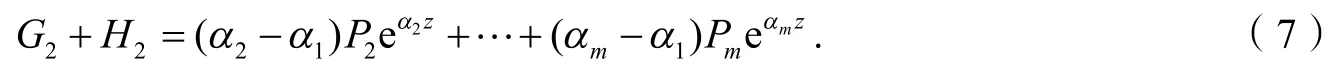
以下分4种情形讨论式（7）.

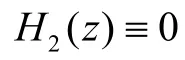
因此，

由式（4）（9）和（10）有：

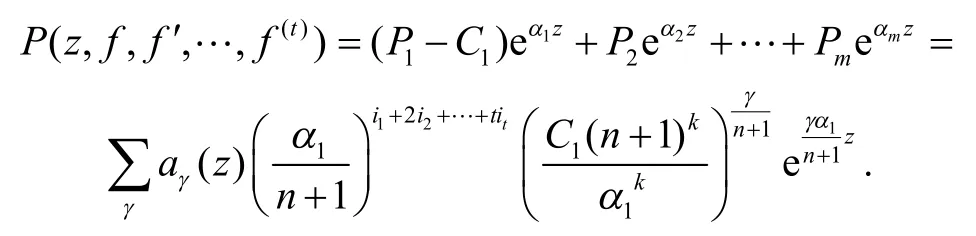
因为γ/(n+1)＜1，所以

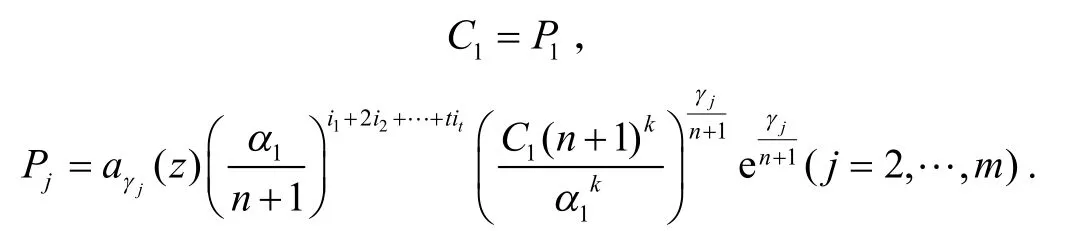
情形4 G2(z),H2(z)均不恒等于0，对方程（7）微分后，得：

由式（7）和（11）消去eα2z，有：

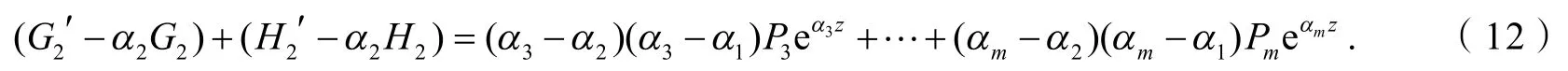
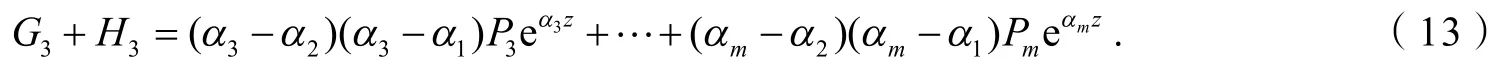
和上面证明类似，对式（13）也分为4种情况进行讨论.

情形4.1 G3(z)≡0和H3(z)≡0是不可能的，因为αj是互不相同的常数.

当m=2时，由式（13）可得 G3+H3=0，与假设矛盾.

当m≥4时，由文献[10]的引理3知：当n≥m≥2时，式（14）不存在超越整函数解.

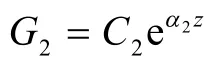
情形4.4 G3(z),H3(z)均不恒等于0，那么方程（13）微分后，得：

由式（13）和（14）消去eα3z，有：

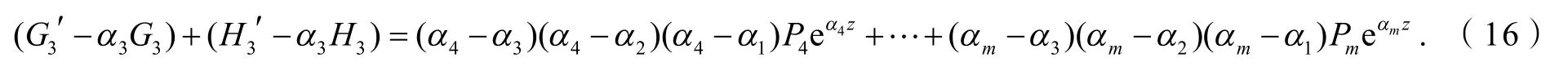
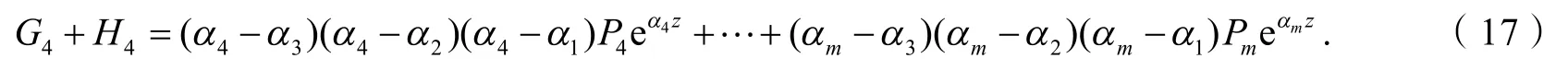
如上，以下分4种情形讨论式（17）.

情形4.4.1 G4(z)≡0和H4(z)≡0是不可能的，因为αj是互不相同的常数.

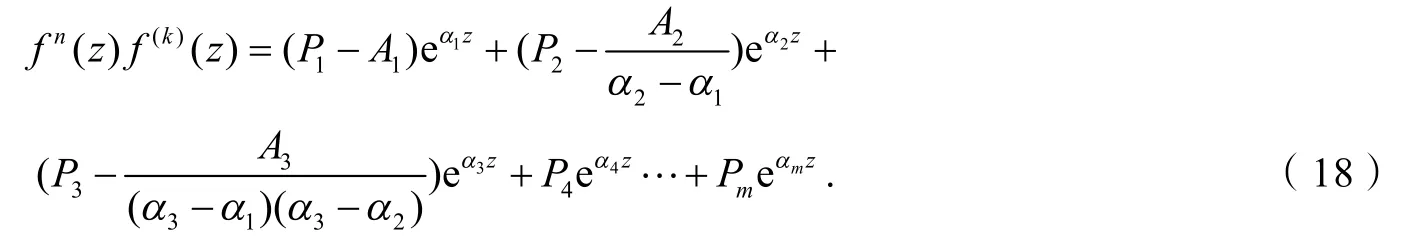
当2≤m≤3时，由式（17）可得G4+H4=0，与假设矛盾.

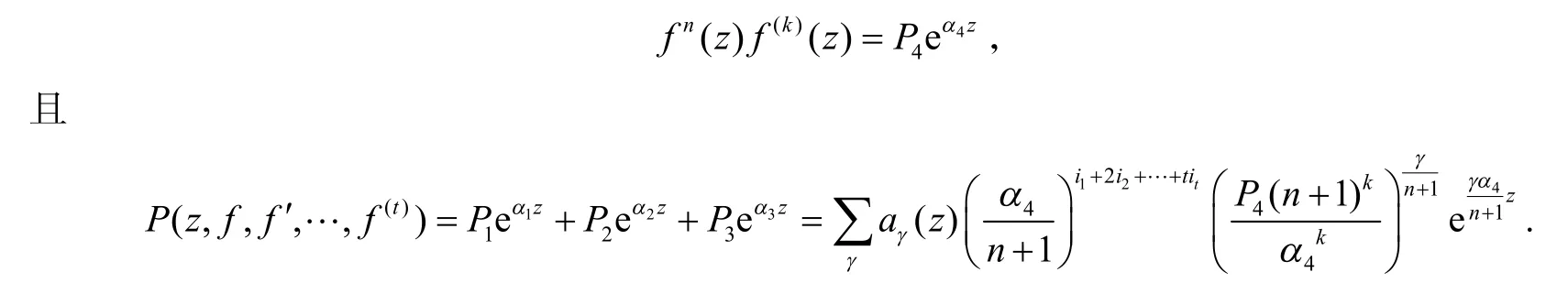
当m≥5时，由文献[10]的引理3知：当n≥m≥2时，式（18）不存在超越整函数解.

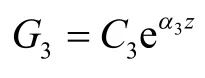
情形4.4.4 G4(z),H4(z)均不恒等于0，那么方程（19）微分后，得：

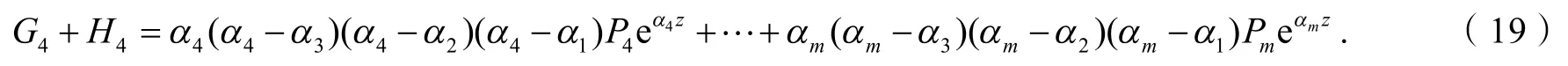
由式（17）和（19）消去eα4z，可得：

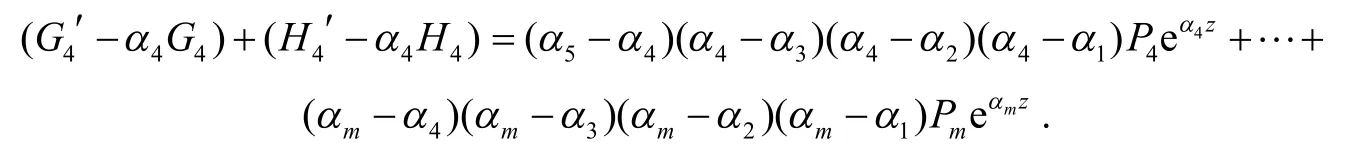
其中，j=5,6,…,m.以下分4种情况讨论.

情况1 Gj(z)≡0和Hj(z)≡0是不可能的，因为αj(j=5,6,…,m)是互不相同的常数.

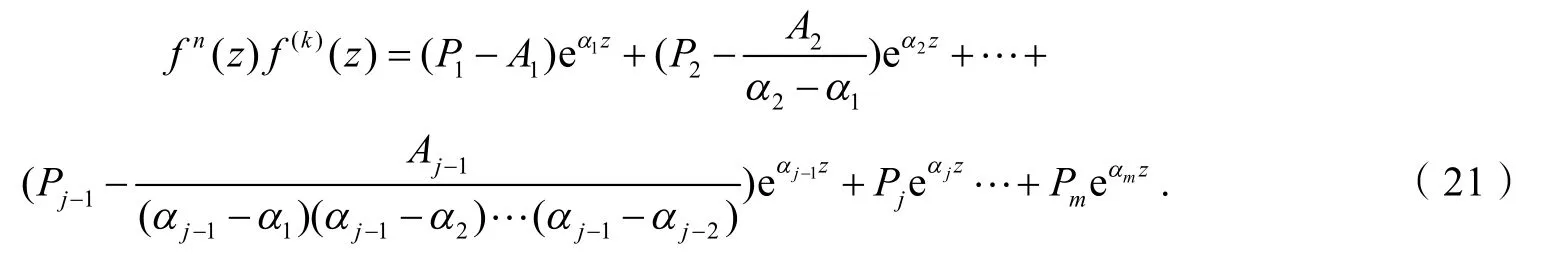
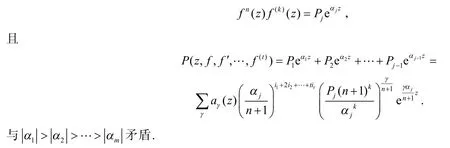
当 m≥j+1时，由文献[10]的引理3知：当n≥m≥2时，式（21）不存在超越整函数解.