四元数双曲空间中的球模型与Siegel域

林伟成，曹文胜

（五邑大学 数学与计算科学学院，广东 江门 529020）

众所周知，秩为1的非紧致对称空间分别是实双曲空间、复双曲空间、四元数双曲空间及Cayley平面[1].Fuchs群和Klein群是分别作用在二维和三维实双曲空间上的离散等距群，这些理论最初是由Poincare和Klein等在19世纪发展起来的.Fields奖获得者Ahlfors、Thurston以及Wolf奖获得者Sullivan等著名学者的工作，使得低维流形与复动力系统、Teichmuller空间、拟共形映射和Klein 群等领域的研究紧密联系在一起.上世纪70年代，Goldman[2]、Kamiya[3]、Parker[4]等数学家开始研究复双曲几何，并得到一些深刻的结果.一维复双曲空间实际上是二维实双曲空间，所以复双曲流形可以看作是双曲黎曼面的一个自然的延伸.实双曲空间可嵌入到复双曲空间，复双曲空间可嵌入到四元数双曲空间.我们知道，实和复双曲几何的思想和方法可为四元数双曲几何的研究指明方向，这些关系使得四元数双曲几何理论越来越受到大家的关注.球模型是四元数双曲空间中的基本模型，已在实和复双曲空间上被深入研究，如Kamiya[5]研究了复双曲空间中球模型与正则域的相交问题，但对四元数双曲空间中球模型的研究目前还处在发展中，其中球模型的极限球以及由球模型引出的 Siegel域的极限球的性质，没有在相关文献中出现.本文主要通过四元数双曲空间上的球模型引入双曲空间的另一模型Siegel域，得到Siegel域上Busemann函数、等距球及极限球坐标等概念，得到四元数双曲空间球模型与 Siegel域之间相关的多方联系.本文定义两模型中的极限球面，并通过Cayley沟通它们之间的对应关系，以期为四元数双曲几何问题的研究提供模型基础.

1 四元数双曲空间的球模型

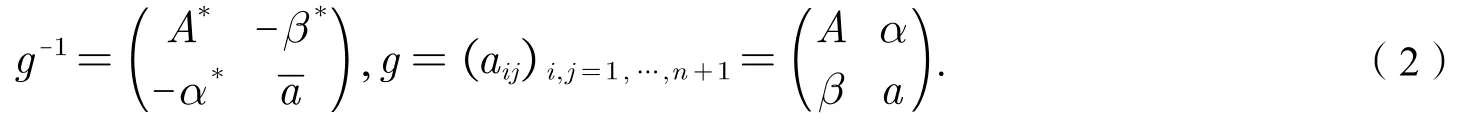
2 四元数双曲空间的Siegel域

由上面的映射S诱导的n+1维四元数向量空间的另一类Hermitian型：

图1 与之间的联系

类似式（1）定义Siegel域上的距离公式：

3 Siegel域上的Busemann函数和等距球

我们定义Siegel域上的Busemann函数[2]如下：

4 Siegel域上的极限球坐标

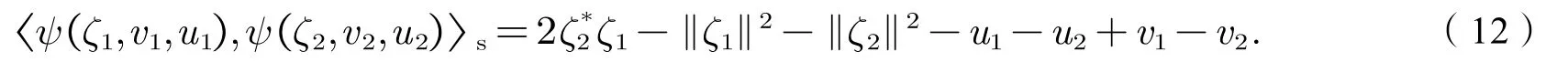
特别地

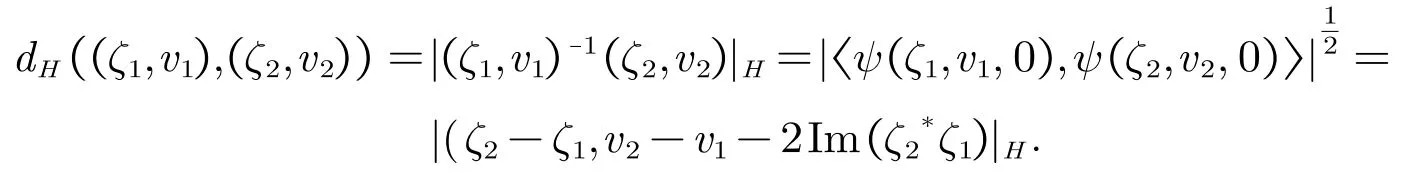
因此有

5 球模型和Siegel域的极限球面