一类双参数奇摄动方程混合三点边值问题

刘 燕，杜冬青

(1.安徽师范大学皖江学院 电子工程系，安徽 芜湖 241000;2.江苏联合职业技术学院 徐州财经分院，江苏 徐州 221000)

源于天体力学和流体力学的奇摄动理论成为处理非线性问题的重要工具,近年来,对于非线性微分方程奇摄动边值问题的研究一直是人们关注的焦点,目前取得了很多的研究成果[1-5].在自然科学领域中,有些奇摄动问题涉及双参数的边值问题,双参数奇摄动问题较单参数奇摄动问题情况复杂,对于双参数奇摄动问题,学者们也做了一些研究[6-9].其中,莫嘉琪[6]研究了一类初值条件的两参数高阶半线性方程奇摄动问题,利用奇摄动方法,得到问题在两个小参数相互关联的三种不同情形下的形式渐近解，并对解的结构做了全面讨论.吴有萍等[7]将初值条件的双参数奇摄动问题推广到非线性边值条件的双参数奇摄动问题,研究了一类具非线性边值条件的三阶方程的双参数奇摄动问题.刘燕等[8]将这类问题进一步推广,研究了一类更为一般的高阶非线性微分方程附以非线性边值条件的双参数奇摄动问题.值得注意的是,对于双参数奇摄动问题的研究主要体现在分离型的边界条件.受以上文献的启发,在Lin等[10]工作的基础上将单参数的奇摄动问题拓展到双参数的奇摄动问题.考虑如下一类具有混合三点边值条件的三阶非线性微分方程的双参数奇摄动问题:

y(0)=μy(η),

(2)

p1y′(0)-p2y″(0)=A,

(3)

y(1)=B,

(4)

其中，p1>0,p2>0,0<η<1,μ<0,ε,λ均是正的小参数,A,B均为常数.

现作如下假设:

(H3) 函数f(x,y),g1(x,y),g2(x,y)的变量在其相应的区域内充分光滑,且各自变量的各阶偏导都有界,并存在正常数l,使得g1(x,y)≤-l,g2y(x,y)>0.

1 外部解的构造

2 边界层的校正项

由假设可知,问题(1)～(4)在x=0和x=1处附近各有一个边界层.首先,在x=0处构造边界层校正项W(τ1,ρ1,ρ2),同时引进伸展变量τ1=x/ρ1,并令

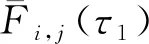
类似地,在x=1处构造边界层校正项V(τ2,ρ1,ρ2),并令

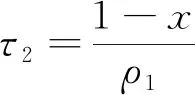
为确定Yi,j(x),Wi,j(τ1),Vi,j(τ2)的定解条件,将

代入式(2)～(4)得 Yi,j(0)=μYi,j(η), i<2,

(19)

Wi-2,j(0)=μYi,j(η)-Yi,j(0), i≥2,

(20)

Y0,0(1)=B,

(24)

Yi,j(1)=0, i<2,

(25)

Vi-2,j(0)=-Yi,j(1), i≥2,

(26)

根据递推方程(7)～(8)、(12)～(13)、(17)～(18)和定解条件(19)～(26)以及式(11)、(16),结合假设(H2)、(H3),运用交替迭代的方法可依次求出Yi,j(x),Wi,j(τ1),Vi,j(τ2),并且有

其中，p(x)是个多项式函数,σ为0<σ<1的常数.根据假设(H1),令

这样得到问题(1)～(4)的N阶形式渐近解.

3 主要结果

再增加如下假设：

定义1[10]对于边值问题：

y(0)=μy(η),

(29)

p1y′(0)-p2y″(0)=A,

(30)

y(1)=B.

(31)

若存在函数α(x),β(x)∈C3[0,1],使得

α(0)≤μα(η),p1α′(0)-p2α″(0)≤A,α(1)≤B,

β(0)≥μβ(η),p1β′(0)-p2β″(0)≥A,β(1)≥B,

则称α(x),β(x)为边值问题(28)～(31)的下解和上解.

引理1[10]若边值问题(28)～(31)满足如下条件:

(A1) 存在下解α(x)和上解β(x)，且当x∈[0,1]时,有α′(x)≤β′(x);

(A2) 函数sgn(y″(x))f(x,y)在[0,1]×[α(x),β(x)]上关于y递减,函数sgn(α′(x))g1(x,y)和g2(x,y)在[0,1]×[α(x),β(x)]上关于y递增;

α(x)≤y(x)≤β(x),α′(x)≤y′(x)≤β′(x),x∈[0,1].

定理1若假设(H1)～(H4)成立,则问题(1)～(4)存在解y(x,ρ1,ρ2)∈C3[0,1],且满足:

证明构造界定函数:α(x,ρ1,ρ2)=yN(x,ρ1,ρ2)-rxρN+1,β(x,ρ1,ρ2)=yN(x,ρ1,ρ2)+rxρN+1,

其中，r为待定的充分大的正常数.

显然有α(x,ρ1,ρ2)≤β(x,ρ1,ρ2),x∈[0,1],α′(x,ρ1,ρ2)≤β′(x,ρ1,ρ2),x∈[0,1],

另外,由微分中值定理可知,存在正常数C1,C2,C3使得

α(0,ρ1,ρ2)-μα(η,ρ1,ρ2)=yN(0,ρ1,ρ2)-μyN(η,ρ1,ρ2)+μrηρN+1≤

A+(C2-p1r)ρN+1,

α(0,ρ1,ρ2)≤μα(η,ρ1,ρ2),p1α′(0,ρ1,ρ2)-p2α″(0,ρ1,ρ2)≤A,α(1,ρ1,ρ2)≤B.

β(0,ρ1,ρ2)≥μβ(η,ρ1,ρ2),p1β′(0,ρ1,ρ2)-p2β″(0,ρ1,ρ2)≥A,β(1,ρ1,ρ2)≥B.

下面证明:

g1(x,yN-rxρN+1)rρN+1-g2y(x,θ)rxρN+1≥

其中，θ∈(α,yN).

当x∈[0,σ]时,由外部解和左边界层的构造知,存在正常数C4和C5,使得

C5ρN+1+MrρN+1=(Mr-C4-C5)ρN+1.

类似地,当x∈[1-σ,1]时,由外部解和右边界层的构造知存在正常数C6,使得

当x∈[σ,1-σ]时,由Wi,j(τ1),Vi,j(τ2)的边界层性态知,存在正常数C7,使得

(Mr-C4-C7)ρN+1,

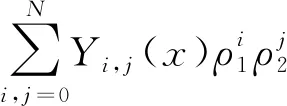
类似可证,当x∈[0,1]时,能够找到充分大的r,使

再由引理1可知,只要r充分大,边值问题(1)～(4)存在解y(x,ρ1,ρ2)∈C3[0,1]，且y(x,ρ1,ρ2)满足: