激光选区熔化多熔道力学现象的解析方法
郭长城(江海职业技术学院机电汽车学院,江苏 扬州 225101)
0 引言
激光选区熔化作为激光增材制造领域中最具发展潜力的技术,其成形件的高致密性是其他激光选区技术无法比拟的。尽管该技术成形件致密度很高,但仍存在影响致密度的球化、孔隙、翘曲、裂纹等缺陷存在,这些缺陷的存在既降低成形件的致密度,也严重地影响了其使用性能[1]。由于激光快速加热和冷却的工艺特点,其形成件凝固后的残余应力是凝固裂纹和翘曲变形[2]产生的根本原因,由此,残余应力也就成为激光选区熔化技术研究热点之一。边培莹等[3]实验结果表明:随着激光功率增大,熔池的几何尺寸和成形件中的残余应力均变大;Wu等[4]实验研究了316L不锈钢棋盘式扫描孤岛面积对残余应力的影响,其结果也是孤岛面积越大,应力越大;Liu等[5]实验结果也说明了:相同功率下扫描速度越慢,残余应力越大,扫描熔道越长,残余应力越大。目前对激光选区熔化技术特点研究更多地是对单熔道而言的,但激光选区熔化成形件是多个熔道搭接而成的,对多熔道的研究更符合实际。为此,在研究单熔道残余应力基础上,有必要开展多熔道残余应力问题研究,以此解释分析熔道的力学现象。
1 熔道搭接几何模型
在激光选区熔化成形过程中,激光作用在金属粉末上,在极短时间内将粉末熔化,然后粉末凝固。随着激光束的移动,成形件以熔道搭接的形式出现,由此也就形成了图1所示的典型激光选区熔化技术熔道搭接横截面形貌[4]。
图1中A、B分别表示某个熔道的搭接区和独立区,其中B区由成形层和与已成形层冶金结合的两部分组成;尽管A的熔道搭接区也存在成形层和已成形层两部分,但更多的是成形层搭接。为了方便力学分析,对图1所示的熔道横截面形貌进行几何模型化处理,这就形成了图2所示的表征形成层熔道之间搭接几何图形模型。

图1 熔道搭接横截面形貌

图2 熔道搭接几何模型
如图2所示,颜色渐变的部分表示激光选区熔化技术已成形的“块体”,借助涂层或薄膜结构理论,它就是涂层或薄膜结构中的基体;“块体”或基体上的搭接半圆集合构成了成形层,每个半圆表示一个熔道,相邻的两个熔道之间的搭接形成了重叠区。图2中的“短竖线”表示重叠区中分线,具体表示为两个搭接的半圆轮廓交点向界面所做的垂线。在该几何图形模型中,此“短竖线”既是相邻两个熔道半圆的几何分界线,也是两个熔道之间热应力相互作用面。图2所示图形不但是多熔道热应力、温度数值模拟计算的几何模型[5]、也是表征成形件表面质量的几何模型[1],这就为相邻两个熔道间残余应力研究奠定了前期熔道搭接几何模型经验基础。
2 力学现象解释
2.1 力学结构模型
根据激光选区熔化成形机理:液态金属对基底润湿能力可用界面热动力学理论来解释[6],即可用图2所示的熔道搭接几何模型中的半圆与基体的已成形层表面之间的接触角大小表征液态金属的润湿性;又鉴于激光选区熔化与激光选区烧结技术的相似性,相邻两熔道搭接关系可用图3所示的两个圆来表示。
如果将两个熔道互为基体表面和金属液滴,则图3也可借界面热动力学理论,用于分析搭接区的能量吸收情况。又根据两球接触力学理论,可进一步将其模型化为具有内聚力影响的两个接触球力学模型。图3中的R、a、δ分别表示模型化的熔道接触球的半径、两个接触球的圆形接触区的半径、两个接触球中心距离O1O2相对变化量。
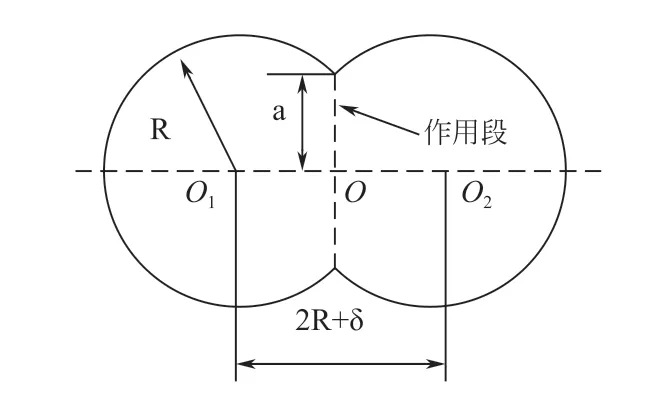
图3 熔道力学结构模型
2.2 接触力学分析
2.2.1 机械相互作用下的接触力学
根据赫兹弹性体接触力学理论,可得图2所示的两个熔道在残余应力相互作用面或图3所示简化的两个圆接触区上的接触应力为:


2.2.2 冶金结合下的接触力学
(1)相邻熔道相互作用力。公式(1)给出的仅仅是考虑相邻两个熔道之间的机械相互作用接触应力,但激光选区熔化技术的相邻两个熔道之间是冶金结合,这就要求激光选区熔化搭接区之间作用力除了残余应力带来的机械接触以外,还存在金属键结合力带来的金属键结合力。这就需要根据激光选区熔化技术特点,对公式(1)作进一步修改。根据界面热动力学理论,两个熔道圆形接触区的单位面积自由能为:

式中:γ、γs、γi分别为圆形接触区相互作用自由能、简化了的熔道球表面自由能和界面自由能。
根据Johnson-Kendall-Roberts 光滑表面接触模型理论,在考虑两个接触球接触作用线上存在金属键结合力情况下,公式(1)上应附加金属键结合应力:


(2)搭接率。图3的两个接触球中心距离O1O2相对变化量δ由如下公式(5)给出。

相邻两个熔道搭接质量往往利用搭接率来表征,其搭接率的几何意义如图4所示。
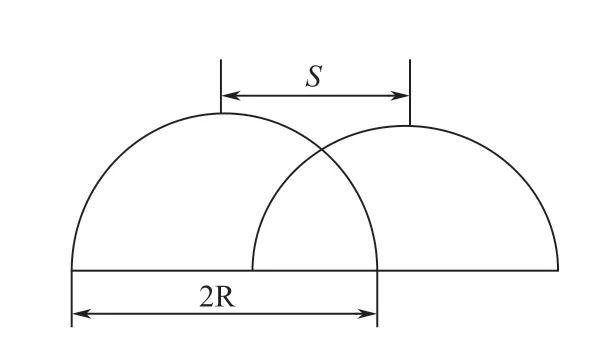
图4 搭接率计算几何图形
相邻两个熔道的搭接率可用公式(6)给出。
式中:R、S分别为熔道的直径和相邻两个熔道中心距。
比较图3和图4可知:公式(6)中的S其实就是图3中的2R+δ,将其及公式(5)带入公式(6)中有:

公式(7)表明:在考虑熔道之间冶金结合和熔道变形时,激光选区熔化的搭接率不但与熔道的几何尺寸有关,也与金属材料性质有关,给优化搭接率工艺参数提供了一个理论基础。
根据断裂力学理论,接触区边缘处的奇异应力场应力强度因子为:
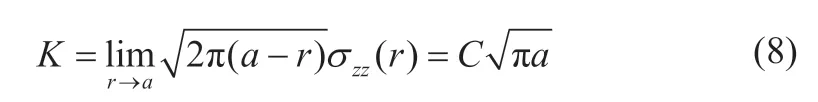
进一步根据线弹性断裂力学理论,接触区域边缘处的单位长度能量释放率为K2/E。由Griffith原理知,能量释放率应等于表面自由能,则有:
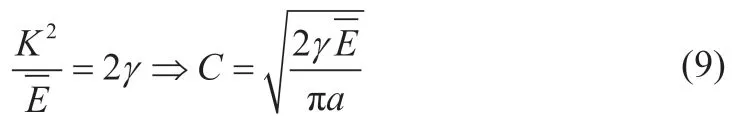
随着公式(7)确定了C值,两个接触球中心距离O1O2相对变化量δ也就随公式(5)确定下来,公式(5)给出了δ与接触区域尺寸a之间的关系。公式(4)也就定量给出了接触区作用合力P与触区域尺寸a之间的关系。一般情况下,公式(4)、(5)之间的关系通过引入公式(8)自然系统的长度量纲无量纲化。

由此,接触区作用合力P、中心距变化量δ及触区域尺寸a可以无量纲化为:

借助上述公式,可将公式(4)转化成:

公式(10)给出了接触区的尺寸与接触区作用合力之间的关系。接触区半径与两个接触球中心距离O1O2相对变化量δ之间的关系是:

由此可见,如果去掉公式(12)、(13)右侧的第二项,公式(12)、(13)就变成了经典赫兹接触力学公式。由此,实现了仅仅考虑机械相互作用的两个相邻熔道之间相互作用力与考虑两个熔道之间冶金结合力的叠加;公式(13)、(14)也说明可以用无量纲的两个接触球中心距δˆ( aˆ)表示搭接率η。
(3)平局残余应力。根据公式(11),接触区作用合力可进一步计算为:

借助公式(11)中的aˆ与R的关系,公式(18)表明:平均残余应力随着熔道面积增加而增加,这与实验结果是一致[7]。又根据考虑具有内聚力影响的两个球接触理论[8],公式(16)所计算的平均应力可以视为熔道的最大残余拉应力,当最大残余拉应力大于熔道材料屈服强度时,熔道就会断裂,产生凝固裂纹,这也与凝固裂纹形成机理相一致的[4]。
3 结语
激光选区熔化多熔道力学现象可借助考虑熔道间的冶金结合的接触力学理论进行解释,这为研究该类问题提供了新的途径。本研究仅仅进行了初步探讨,下一步需要借助实验和数值模拟做一步深化研究。

