求解线性方程组稀疏解的稀疏贪婪随机Kaczmarz算法

王 泽，殷俊锋

（同济大学数学科学学院，上海 200092）

求解线性方程组Ax=b的稀疏解在图像重构、信号处理和机器学习中具有广泛应用［1-4］。通过引入l1-范数，求解线性方程组的稀疏解可以转化为求解式（1）正则化最小二乘问题：

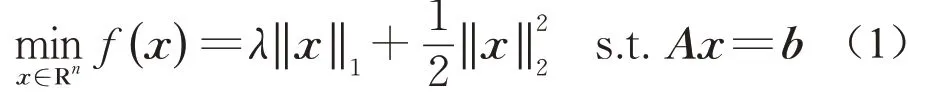
求解该问题常见的算法包括基追踪方法、Bregman方法、共轭梯度方法等［5-7］。

自Strohmer和Vershynin［8］证明了随机Kaczmarz算法具有线性收敛率以来，许多专家学者对随机Kaczmarz算法进行了深入的研究［9-11］。Kaczmarz算法求解的是最小二乘解，通常是稠密的，为了求解线性方程组的稀疏解，文献［12］提出稀疏Kaczmarz算法，该算法在原有的Kaczmarz算法基础之上引入了软阈值函数，解决了最小二乘解稠密性的问题。

在线性方程组相容的情况下，文献［13］证明了稀疏Kaczmarz算法迭代收敛到问题（1）的唯一解。令右端噪声项bδ满足‖b−bδ‖2≤δ时，线性方程组可能不相容，文献［14-15］证明了随机Kaczmarz算法的迭代值依期望收敛，并且与无噪声情况下有相同的收缩因子。文献［16］在稀疏Kaczmarz算法基础之上，提出了随机稀疏Kaczmarz算法，并在有噪声干扰和无噪声干扰的情况下给出了随机稀疏Kaczmarz算法的收敛性分析。当系数矩阵的行范数相差较小时，随机Kaczmarz算法将等概率选取A的行，此时随机Kaczmarz算法的收敛速率较慢，因此Bai和Wu［17］结合贪婪和随机思想，提出一种新的概率准则来选取工作行，形成贪婪随机Kaczmarz算法。更多贪婪随机Kaczmarz算法的研究参见文献［18-21］。

在稀疏随机Kaczmarz算法的基础之上［21］，受贪婪算法的启发，本文提出稀疏贪婪随机Kaczmarz算法，给出稀疏贪婪随机Kaczmarz算法在有噪声干扰和无噪声干扰情况下的收敛性分析，并以大量的数值实验验证本文算法的计算效率。

符号标记如下，定义为线性方程组Ax=b的解，其中A∈Rm×n，b∈Rm，a i表示系数矩阵A的第i行。支持集S=supp()={j∈{1，…，n}≠0}是列向量x中非零元的下标所构成的集合，A S是A的子矩阵，由支持集S中的指标选取系数矩阵A的列构成，a iS表示的是A S的第i行，x S是在支持集S限制下的列向量；定义(A)=min{σmin(A J)∣J⊂{1，…，n}，A J≠0}为子矩阵A J的最小奇异值，其中A J为指标集J中A的列构成的子矩 阵，令；⊙为哈达玛积（Hadamard product）；为对支持集大小的估计值；w j为稀疏随机Kaczmarz算法第j次迭代的权重值，w j∈Rm×1。

1 稀疏贪婪随机Kaczmarz算法

当Ax=b的解x稀疏时，文献［21］提出了稀疏随机Kaczmarz算法，加快了算法的收敛速率（算法1）。

算法1稀疏随机Kaczmarz算法［21］。①输入A∈Rm×n，b∈Rm，最大迭代数M和估计的支持集的大小。②输出x j。③初始化S={1，…，n}，x0=0，j=0。④当j≤M时，置j=j+1。⑤选择行向量a i，i∈{1，…，n}，每一行对应的概率为。⑥确定估计的支持集⑦生成权重值⑨转步骤④。

稀疏随机Kaczmarz算法可以用比随机Kaczmarz算法更少的迭代步数找到最小二乘解。由于支持集和稀疏度都是未知的，因此稀疏随机Kaczmarz算法从支持集中所有元素的稀疏度的初始估计开始，然后在每一次迭代中，稀疏随机Kaczmarz算法通过去掉向量x中数量级最小的元素下标来更新估计的支持集。该算法第j次迭代的加权准则为

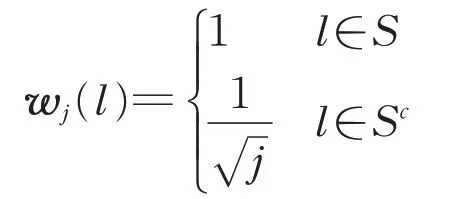
其中，j为迭代步数。当j→∞时，w j⊙a i→a iS，因此原线性方程组退化成

由于κ(A S)≤κ(A)，因此稀疏随机Kaczmarz算法的收敛因子小于随机Kaczmarz算法。但是由于最小二乘解总是稠密的，该算法在求解超定线性方程组时，虽然在稀疏解零元对应位置上的元素很小，但仍然不等于零，因此在文献中提出稀疏Kaczmarz算法，文献［16］在稀疏Kaczmarz算法的基础上，提出了随机稀疏Kaczmarz算法（算法2）。

算法2随机稀疏Kaczmarz算法［16］。①输入A∈Rm×n，b∈Rm，最大迭代数M。②输出x k。③初始化：x0=x*0=0。④置k=0，当k≤M−1时。⑤选择行向量a ik，ik∈{1，…，n}，每一行对应的概率为x k+1=Sλ(x*k+1)。⑧转步骤④。

算 法 2中λ＞0，Sλ(x)=max{|x|−λ，0}⋅sign(x)。结合稀疏随机Kaczmarz算法和随机稀疏Kaczmarz算法的思想，受贪婪算法的启发，本文提出稀疏贪婪随机Kaczmarz算法，在保证算法能够计算出稀疏解的同时，通过贪婪的概率准则来选择工作行从而达到加快算法收敛速度的目的。算法3给出稀疏贪婪随机Kaczmarz算法。

算法3稀疏贪婪随机Kaczmarz算法。①输入A∈Rm×n，b∈Rm，最大迭代数M和估计的支持集的大小k。②输出x k。③初始化S={1，…，n}，x0=x*0=0。④置k=0时，当k≤M−1时。⑤计算

⑥决定正整数指标集

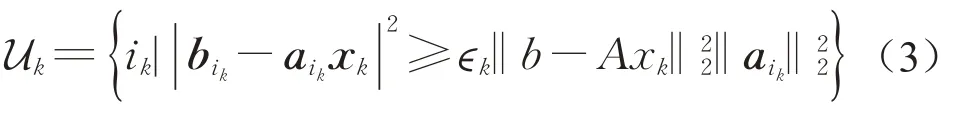
⑦计算向量的第i行

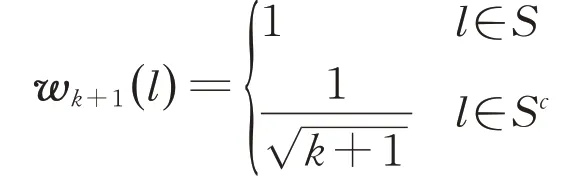
⑪计算

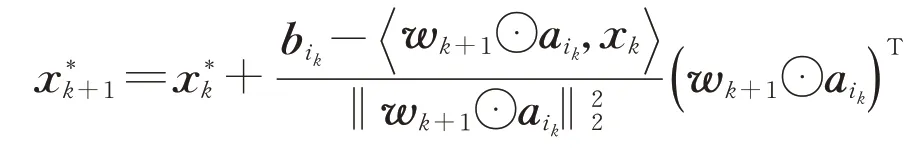
⑫计算x k+1=Sλ(x*k+1)。⑬转步骤④。

2 稀疏贪婪随机Kaczmarz算法的收敛性分析

为了证明求解正则基追踪问题（1）稀疏贪婪随机Kaczmarz算法依期望线性收敛，先回顾一些基本的概念和性质［22］。

令f：Rn→R是凸函数，用∂f(x)表示f在x∈Rn的次微分

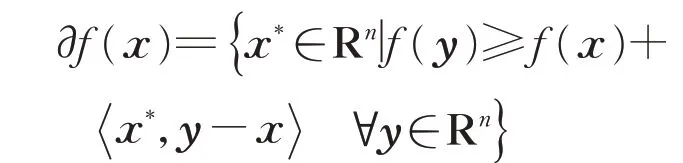
其中，∂f(x)是一个非空紧凸集。

定义1凸函数f：Rn→R，如果存在α＞0，使得对任意的x，y∈Rn且x*∈∂f(x)，有

那么f是强凸的，当和α的具体值相关时，则称f是α-强凸的。

定义2［22］如果f：Rn→R是α-强凸，那么它的共轭函数f*(x*)：=supx∈Rn x*，x−f(x)可微且有1/α−Lipschitz连续梯度，例如

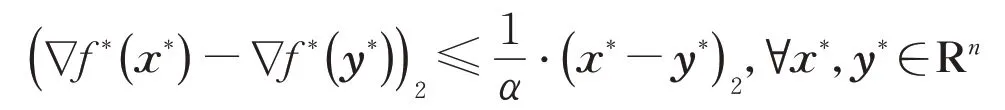
有式（4）不等式成立：

定义3令f：Rn→R是强凸函数，那么x，y∈Rn之间的Bregman距离由f和一个次梯度x*∈∂f(x)定义

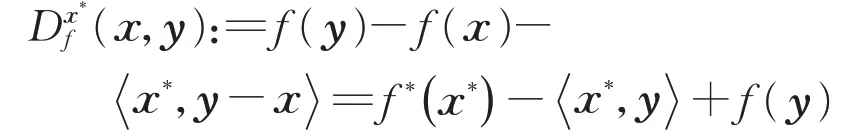
如果f是可微的，那么有∂f(x)={∇f(x)}，因为D f(x，y)=f(y)−f(x)−，所以可以简化来写Df(x，y)=Dx*f(x，y)。

下面的引理都遵循强凸性的假设［13］，给出了随机方法收敛性分析所需的Bregman距离的关键性质。

引理1［13］令f：Rn→R是α强凸函数，对任意的x，y∈Rn和x*∈∂f(x)、y*∈∂f(y)有

因此

对于序列x k和xk*∈∂f(x k)，(x k，y)的有界性意味着x k和x*k有界。如果f有一个L-Lipschitz连续梯度，那么也有

定义4令f：Rn→R是强凸函数，且C⊂Rn是一个非空闭凸集，则x到C上的Bregman投影是关于f和x*∈∂f(x)满足下式的唯一点对于可微的f，可以简化为ΠC(x)和distf(x，C)。

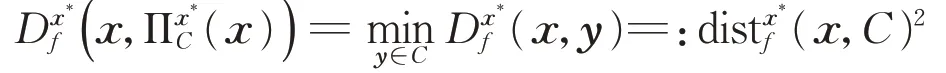
引理2［13］令f：Rn→R是强凸函数，x到C上的Bregman投影点∈C是与f和x*∈∂f(x)相关，当且仅当存在一个∈∂f()满足式（5）或式（6）：

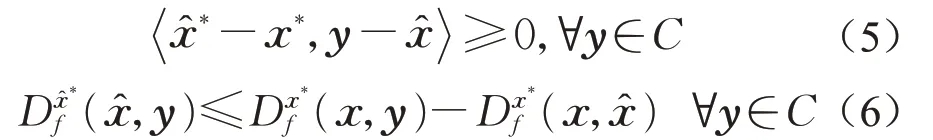
可以叫这样的点是的可允次梯度。

引理3表明，Bregman投影到仿射子空间和半空间可以通过求解可微共轭函数f*的无约束优化问题来计算。

引理3［13］令f：Rn→R是α-强凸函数，A∈Rm×n，b∈Rm，u∈Rn和β∈R。

（1）x∈Rn到仿射空间L(A，b)：={x∈Rn|Ax=b}≠∅的Bregman投影是

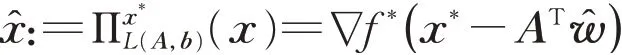
其中∈Rm是下式的解：

更重要的是，根据引理2，：=x*−AT是的可允次梯度。如果A行满秩，那么对任意的y∈L(A，b)有

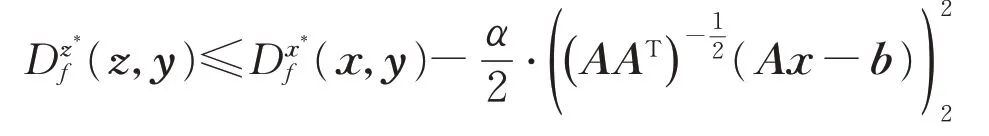
（2）x∈Rn到超平面H(u，β)：={x∈ Rn∣u，x=β}满足u≠0的Bregman投影是

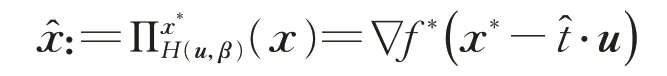
其中∈R是下式的解：

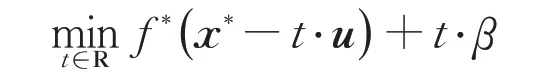
更重要的是：=x*−⋅u是的可允次梯度，对任意的y∈H(u，β)有

如果x不是在半空间H≤(u，β)：={x∈Rn∣u，x≤β}，那么有必要满足＞0，(x)=且上面的不等式对任意的y∈H≤(u，β)都成立。

引理4［16］对于任意的x∈Rn满 足∂f(x)∩R(AT)≠∅ 和任意的x*=ATy∈∂f(x)∩R(AT)，有

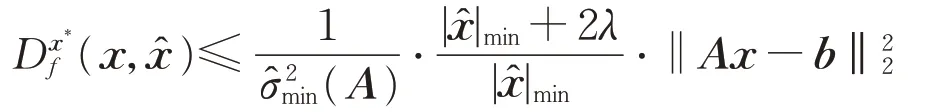
定理1（无噪声情况）令稀疏贪婪随机Kaczmarz算法所产生的迭代序列x k依期望线性收敛到唯一解，其收缩因子为

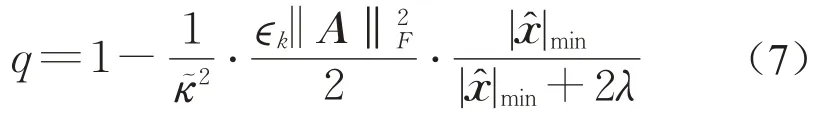
从而

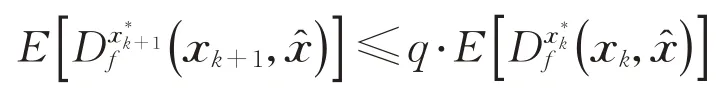
且

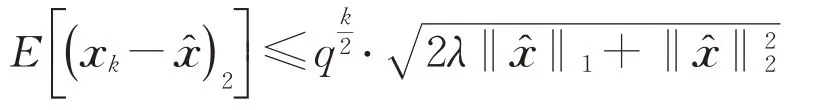
证明根据引理3的（2）中的估计，有式（8）成立：

对式（8）两边同时取条件期望有

根据式（2）和式（3）的定义，有不等式（10）成立：

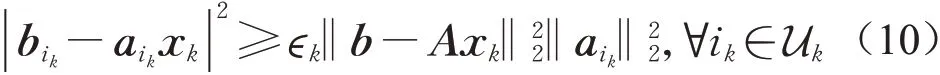
将式（10）代入到式（9）中，从而有

由式（11）的推导，可以得出

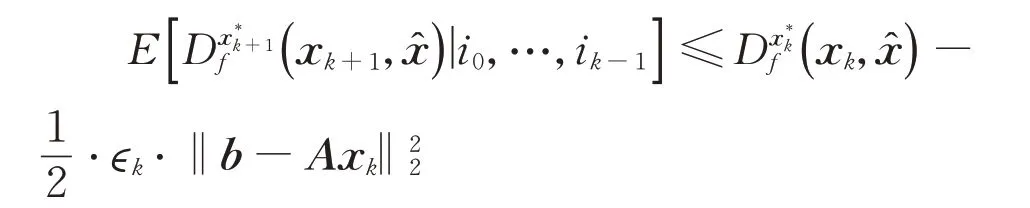
根据引理4有

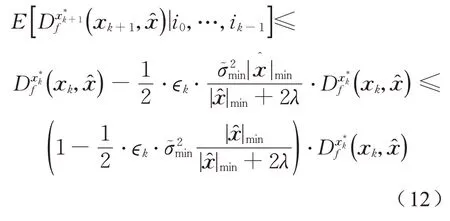
根据引理1，令α=1可得

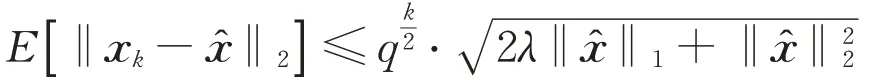
证毕。

定理2（有噪声情况）已知右段噪声项bδ∈Rm满足‖b−bδ‖2≤δ。如果稀疏贪婪随机Kaczmarz算法的迭代值x k由bδ替代b来计算，那么有噪声干扰和无噪声干扰有相同的收缩因子

证明令

和式（8）相类似有

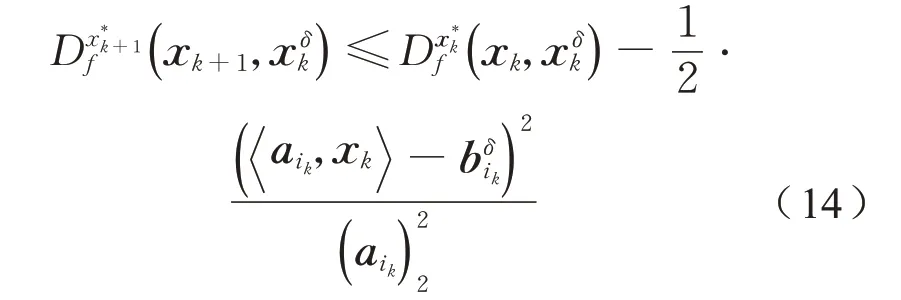
将式（14）进行简单的变换等价于式（15）：

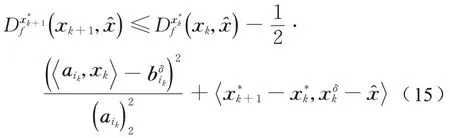
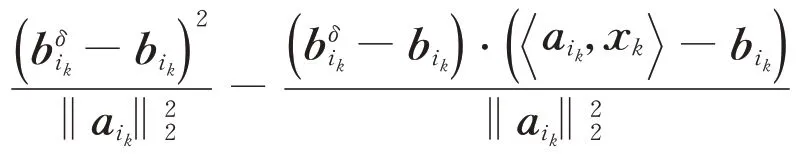
而

所以

类似于无噪声情况的证明方法可以得到

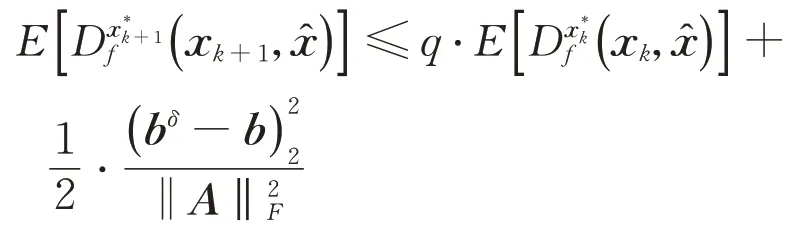
通过归纳得出

由引理1，令α=1，且，有

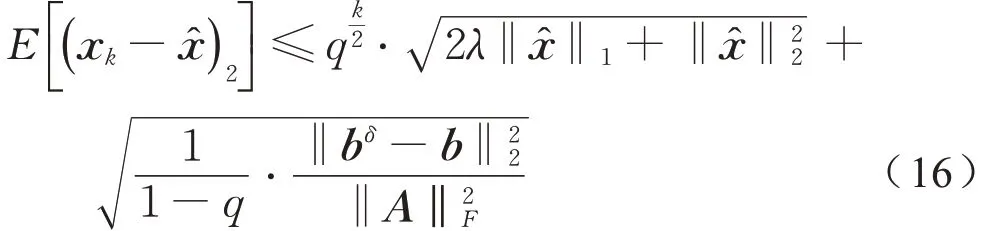
证毕。

注意到稀疏贪婪随机Kaczmarz算法的收缩因子为

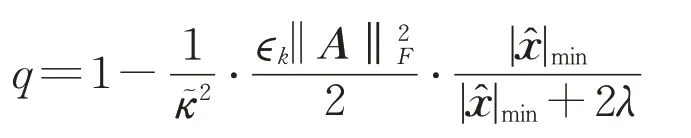
文献［16］定理3.2中随机稀疏Kaczmarz算法的收缩因子为

因

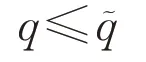
由此可以得出稀疏贪婪随机Kaczmarz算法的收缩因子小于随机稀疏Kaczmarz算法的收缩因子。一般而言，收缩因子越小，收敛速度越快，因此理论分析表明稀疏贪婪随机Kaczmarz算法收敛速度会比原有的随机稀疏Kaczmarz算法的收敛速度更快。

3 数值实验

通过随机生成的高斯矩阵和矩阵市场中的矩阵2个数值实验算例来比较稀疏贪婪随机Kaczmarz（SGRK）算法、随机稀疏Kaczmarz（RaSK）算法和稀疏随机Kaczmarz（SRK）算法的收敛速度。为了能够使三者收敛到相同解上进行比较，在本次数值实验中，在稀疏随机Kaczmarz算法最后一步加上了软阈值函数Sλ(x)参与迭代以保证求得稀疏解。对相同参数的同一个线性方程组Ax=b做了20次试验，得到迭代步数（IT）和CPU计算时间的平均值。解的相对误差（RSE）定义为

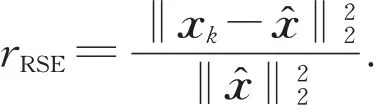
例1利用Matlab软件中的randn函数随机生成系数矩阵A和x n×1，其中有k×n个非零元，之后利用b=A×x得到相容线性方程组，初始向量x0=0。取k=2×k，通过k来设置解的稀疏度，其中k͂是对稀疏度的初始估计值。

当解稀疏度为0.2、0.4、0.6以及0.8时，表1和表2分别给出了系数矩阵A的维数为1000×150和4000×300时的SGRK算法、RaSK算法和SRK算法的迭代步数和计算时间。

当稀疏度为0.2和0.8时，图1和图2分别给出系数矩阵A的维数为1 000×150和4 000×300时3种算法近似解的相对误差随迭代步数变化的曲线。

通过表1和表2中的实验数据以及图1和图2中的变化曲线可以看出，随着稀疏解非零元个数的不断增加，SRK算法的收敛曲线不断向RaSK算法的收敛曲线靠拢，这是因为SRK算法在对应零元位置上乘以权重，加速减小零元位置上的元素，因此在零元较多的情况下，SRK算法的收敛速度更快。但是，由于SRK算法的计算过程较为复杂，因此在计算时间上一开始低于RaSK算法，后来在迭代步数不明显占优的情况下，计算时间要多于RaSK算法。SGRK算法在2种算法的基础之上，每次以贪婪的概率准则随机选取行指标进行迭代，因此SGRK算法的计算时间和迭代步数都要优于其他2种算法。

图1 当矩阵A的维数为1 000×150时SGRK、RaSK和SRK算法的收敛曲线Fig.1 Convergence curves of SGRK,RaSK and SRK methods for Example 1 at a matrix A of 1 000×150

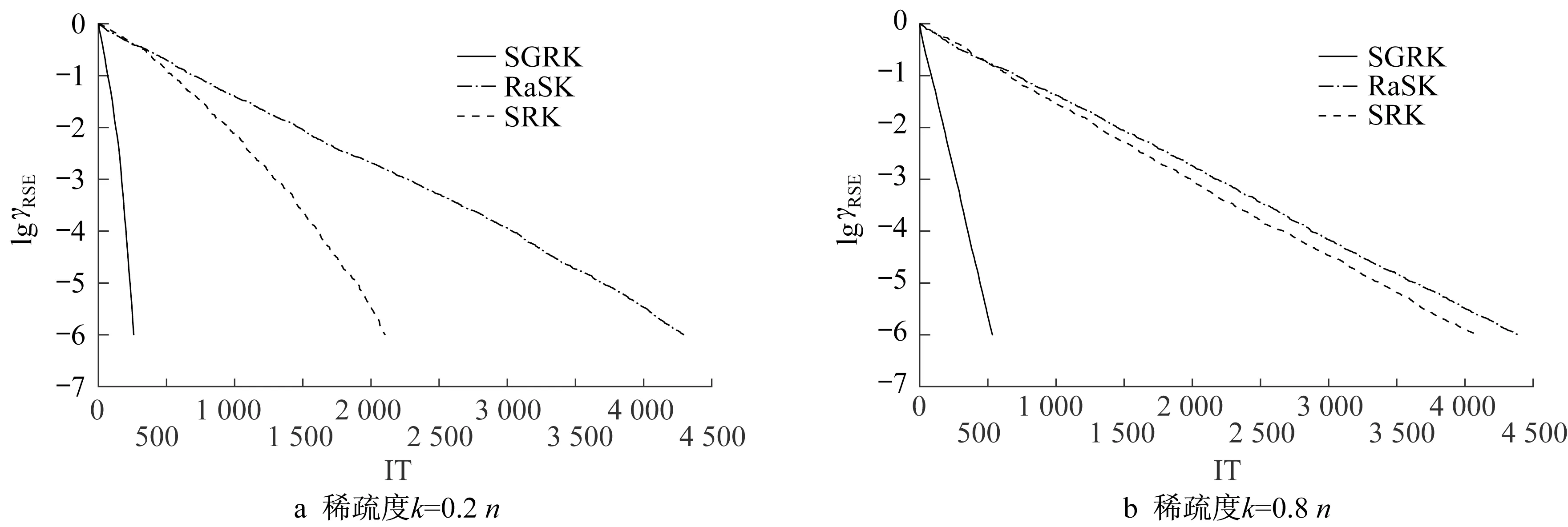
图2 当矩阵A的维数为4 000×300时SGRK、RaSK和SRK算法的收敛曲线Fig.2 Convergence curves of SGRK,RaSK and SRK methods for Example 1 at a matrix A of 4 000×300

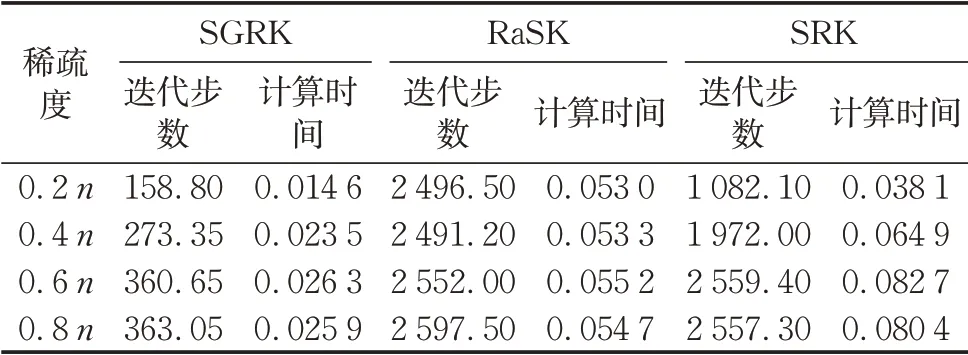
表1 m=1 000、n=150时SGRK、RaSK和SRK的迭代步数和计算时间Tab.1 Iteration steps and computation time of SGRK,RaSK and SRK（m=1 000、n=150）

表2 m=4 000、n=300时SGRK、RaSK和SRK的迭代步数和计算时间Tab.2 Iteration steps and computation time of SGRK,RaSK and SRK（m=4 000、n=300）

例2选取了矩阵市场中的一些矩阵进行数值实验。为了得到超定的系数矩阵，将所有的欠定矩阵取转置之后再做数值实验，取稀疏度估计为k=2k，稀疏度k=0.2n。表3列出的是测试矩阵的相关信息。

表3 矩阵信息Tab.3 Matrix information for Example 2

对于测试的矩阵，表4给出了SGRK算法、RaSK算法和SRK算法的迭代步数和运行时间。

图3对应于表4，给出了3种算法近似解的相对误差随着迭代步数的变化曲线。通过对比可以发现，在无噪声干扰的情况下，SGRK算法的迭代步数和CPU运行时间都优于原来的RaSK算法和SRK算法。

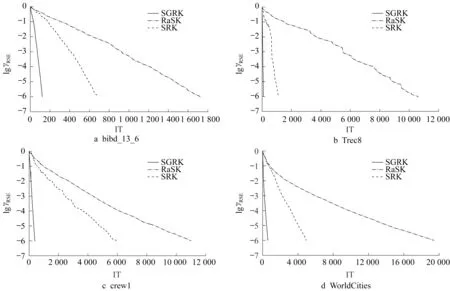
图3 SGRK、RaSK和SRK算法在稀疏度k=0.2 n时的收敛曲线Fig.3 Convergence curves of SGRK,RaSK and SRK methods convergence curve for Examples 2 at a sparsity k=0.2 n

表4 SGRK、RaSK和SRK的迭代步数和计算时间Tab.4 Iteration steps and computation time of SGRK,RaSK and SRK

图4和图5描述SGRK算法、SRK算法和RaSK算法在有噪声干扰的系统中的一些数值实验结果。用Matlab软件中的randn随机生成高斯矩阵和范数为0.02的独立高斯噪声进行数值实验。

图4和图5中水平的实线是SGRK算法的相对误差阈值，水平的虚线是RaSK算法的相对误差阈值，图4是在有噪声干扰的情况下，解的稀疏度为0.2时3种算法的近似解的相对误差随迭代步数的变化曲线。其中图4a描述系数矩阵A的维数为1 000×150时的收敛情况，图4b描述的是系数矩阵A的维数为4 000×300时的收敛情况。

图5是在有噪声干扰的情况下，解的稀疏度为0.6时3种算法的近似解的相对误差随迭代步数的变化曲线。其中图5a和图5b分别画出的是系数矩阵A的维数为1 000×150和4 000×300时3种算法的收敛曲线。

由图4和图5可以看出，在有噪声干扰的情况下，SGRK算法优于其他2种算法最先达到稳定阈值。另外，在图4和图5中分别用水平的实线和虚线画出了SGRK算法的相对误差阈值和RaSK算法的相对误差阈值，通过数值实验表明，由定理2中SGRK算法推导出来的阈值更接近实际情况。

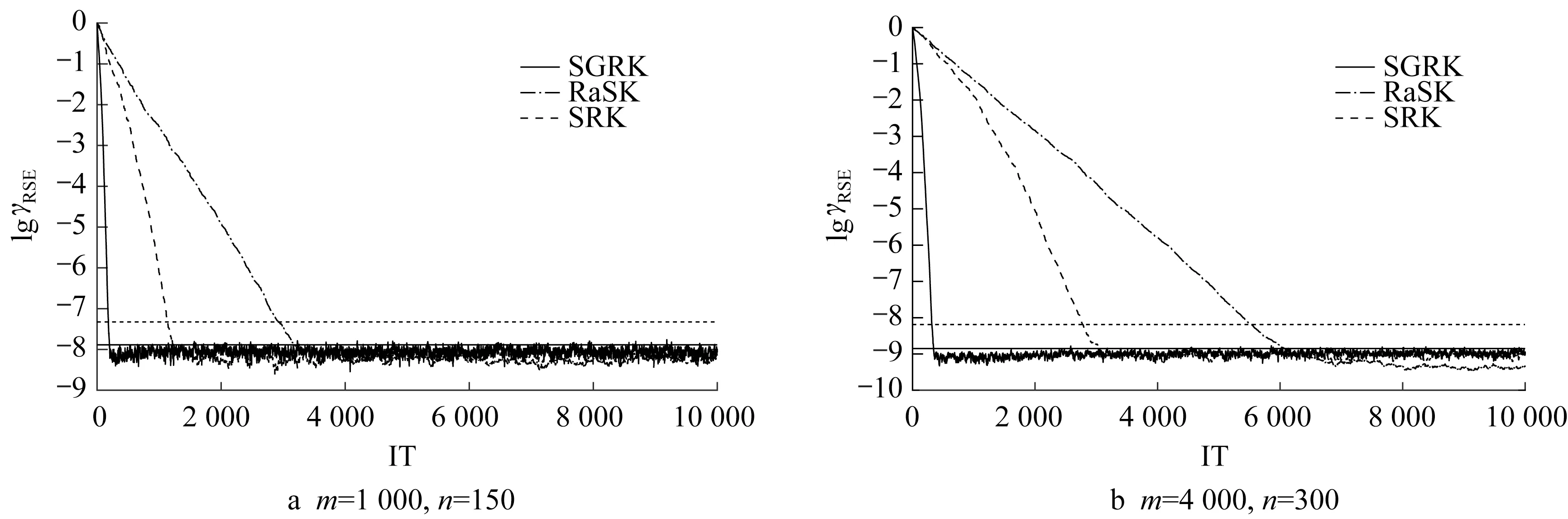
图4 SGRK、RaSK和SRK算法在稀疏度k=0.2 n时误差阈值和实际误差比较Fig.4 Comparison of error threshold and actual error of SGRK,RaSK and SRK methods at a sparsity k=0.2 n

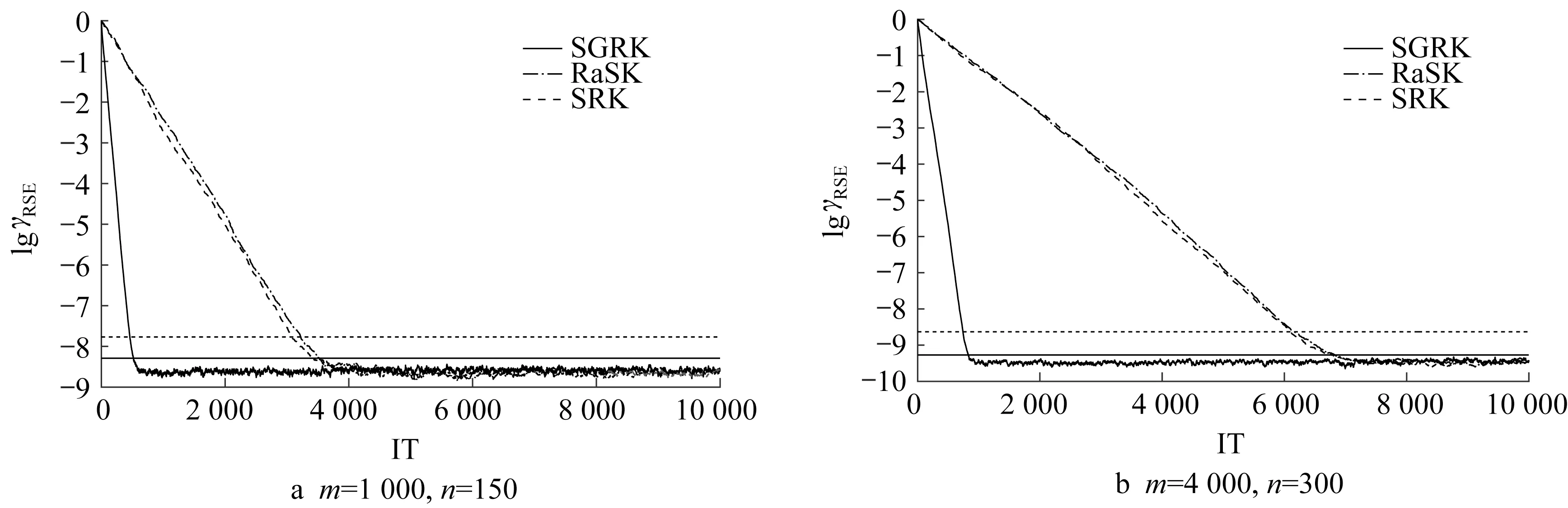
图5 SGRK、RaSK和SRK算法在稀疏度k=0.6 n时误差阈值和实际误差比较Fig.5 Comparison of error threshold and actual error of SGRK,RaSK and SRK methods at a sparsity k=0.6 n

4 结论

在随机稀疏Kaczmarz算法和稀疏随机Kaczmarz算法的基础上，受贪婪算法的启发，提出稀疏贪婪随机Kaczmarz算法，给出了新算法的收敛性分析，且在有噪声干扰和无噪声干扰的情况下，通过理论证明了新算法的收缩因子小于随机稀疏Kaczmarz算法的收缩因子。数值实验表明所提出的新算法在迭代步数和计算时间上均优于传统的随机稀疏Kaczmarz算法。

作者贡献声明：

王 泽：算法设计者和算法研究的执行人，构造新的算法，给出收敛性证明，完成数值实验和数据分析、论文初稿的写作。

殷俊锋：研究的构思者及负责人，指导实验设计，数据分析，论文写作与修改。