多孔岩体蠕变诱发延迟压实局部化失稳特性

薛大为，吕玺琳，任中俊，刘泳钢

（1.同济大学岩土及地下工程教育部重点实验室，上海 200092；2.同济大学土木工程学院，上海 200092；3.湖南科技大学土木工程学院，湖南湘潭 411201；4.四川省建筑科学研究院，四川成都 610084）

自然界中多孔岩体（如砂岩）在受荷变形过程中可能发生局部化［1］，其通常表现为塑性（或损伤）应变和位移场的局部化分布，并伴随着局部化带内孔隙塌陷，亦可称为“压实局部化失稳”［2］。压实局部化变形模拟和预测对于地球物理和岩土工程问题具有重要意义，如斜坡、隧道的稳定性以及天然气回收、二氧化碳储存等都可能遇到与之相关的问题。

近年来有关加载诱发的局部化变形研究方面取得较大进展，室内试验中已成功观察到多孔岩体在压实过程中形成的压实带，其发生表现为孔隙塌陷和颗粒破碎为特征［3-6］。Liu等［7］的研究表明，多孔岩体中可出现具有非零倾角的剪切增强压实带和完全垂直于最大主应力方向的纯压实带。当前脆性岩土材料的延迟失稳也逐渐成为一个热门研究领域（如岩石［8-9］及多孔岩体［10］）。多孔岩体在蠕变过程中，由于其随时间变化的特性，往往会发生以加速变形为特征的自发性失稳［10］。多孔岩体中微结构的存在导致了延迟压实局部化的形成，且伴随显著的带内应变加速演化现象。Heap等［11］研究了蠕变试验中加速变形的时间演化和纯压实局部化带的起始和扩展。Brantut等［10］的试验研究结果表明，具有非零倾斜角度的剪切增强型压实带也能被蠕变激活。

有关多孔岩体压实局部化的理论判别方面，通过弹塑性理论框架下的变形分叉理论或可控性分析，可预测加载导致的压实局部化起始点［12-14］。然而，弹塑性框架不能反映多孔岩体随时间变化的力学特性，因此需要使用弹黏塑性理论。在弹黏塑性框架下，由于无法直接定义增量应力和增量应变关系的刚度矩阵，导致分叉理论和可控性理论不再适用。Pisano等［15］通过多个常微分方程系统提供了一种识别弹黏塑性固体在稳态外部摄动（即蠕变条件）下应变加速（即应变不稳定演化）和减速（即应变稳定演化）的可能方法。结合特定的运动学约束，该方法已被成功用于分析饱和及准饱和黏土的延迟分散性型失稳［16］以及多孔岩体中纯压实带的理论判别中［14］。然而，现有的研究并没有考虑具有非零倾角的剪切增强压实局部化情形。

本文提出一个黏塑性压实局部化失稳指数，用于表征率相关多孔岩体中拟瞬时局部化和延迟局部化。基于黏塑性可控性理论，建立非线性常微分方程系统，将响应变量的加速度与响应变量率联系起来。推导该系统的失稳指数，用于识别自发传播的压实局部化带内不稳定加速变形响应，并通过本构模拟和有限元数值模拟对所提出失稳指数的合理性进行了验证。

1 蠕变条件下压实局部化触发条件

在定常外部摄动下（即蠕变），多孔岩体可发生以应变加速为特征的延迟压实局部化失稳。在这一过程中，压实带内的本构响应可表示为

式中：及为加载应力率和加载应变率；相应地，及为响应应变率和响应应力率；De为弹性矩阵；及为黏塑性应变率。

考虑到广义压实带以狭窄区域内密集的局部变形为特征，因此可利用简单剪切模式来描述带内的运动变形特性，如图1所示。

图1 压实局部化带内简单剪切运动学示意图Fig.1 Schematic diagram of simple shear kinemat⁃ics inside compaction localization bands

从图1可看出，带内变形受到法向应力率及切向应力率控制；与此同时，还需要满足平面应变条件及简单剪切变形约束。因此，压实带内的控制加载变量率和响应变量率可表述为

式（1）中，黏塑性应变率通过过应力方法计算得到

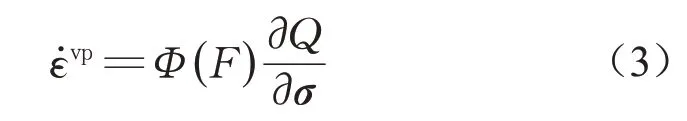
式中：Φ(F)为黏性核函数，其大小取决于非弹性应力状态（即所谓的过应力）与屈服面之间的距离；Q(σ)为塑性势函数。为考虑具有任意倾角的压实带，需要进一步考虑旋转参考系统，旋转角度即压实带的倾角，可通过方向余弦矩阵T对参考系统施加旋转［16］。相应地，旋转应力率、应变率、弹性矩阵可表示为

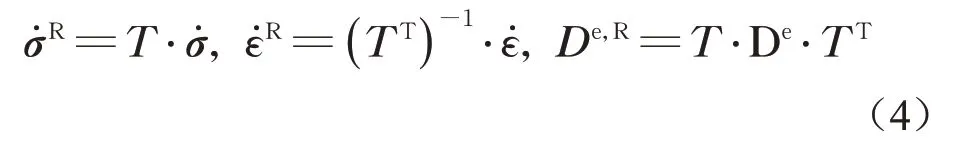
式中

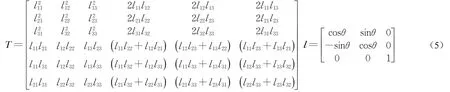
式中：θ为压实带倾角；K和G分别为弹性体积模量及剪切模量。

显然，式（1）-（4）描述了多孔岩体压实带内的本构特性。利用上述公式推导出响应变量率ε̇α及σ̇β为

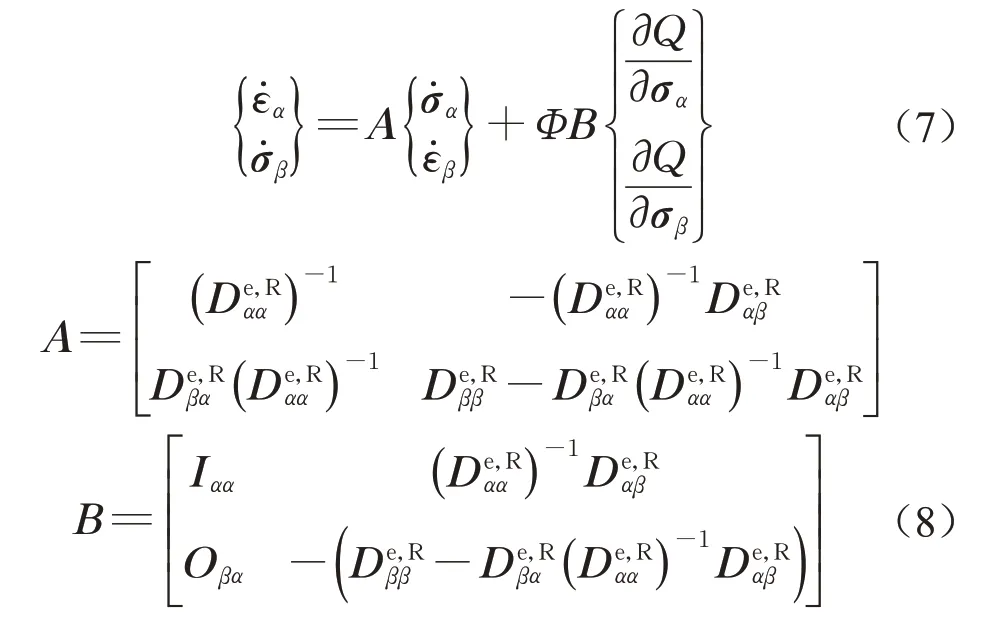
式中：Iαα和Oβα分别为单位矩阵及零矩阵。进一步地，可推导得到响应变量的演化加速度

式中：和为体力项，在蠕变条件下为零。考虑简单剪切条件（即=0）及定常外部摄动条件（即蠕变=0），式（9）可转化为

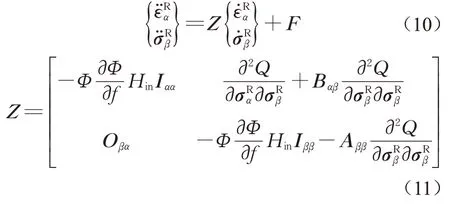
在蠕变条件下有

式中：H为硬化模量；Hχ与式（2）、式（3）中的控制加载变量及响应变量的具体形式相关，亦可称为可控性模量。

最终，控制响应变量变速演化规律的常微分方程系统得以建立。式（10）通过依赖时间变化的矩阵Z（即弹黏塑性本构算子）控制响应变量的变速演化规律。若矩阵Z的特征值为负，则响应变量将呈现减速演变，可视为稳定响应；然而若矩阵Z的特征值为正，将导致响应变量速率的加速演变，可视为不稳定响应。式（10）表明，矩阵Z的特征值由Zαα和Zββ的特征值组成。Zαα为对角矩阵且特征值的正负号由H in控制；而Zββ为一个对角矩阵和一个海森矩阵之和。由于塑性势函数为凸函数，海森矩阵的特征值为恒正，因此Zββ的特征值永远小于Zαα的特征值。这就意味着当Hin＞0时，响应变量呈现减速演化趋势，即该系统是恒稳定的；相反，当Hin＜0时，响应变量速率有加速发展的潜在可能，意味着系统是潜在不稳定的。因此，Hin＞0是弹黏塑性材料稳定的充分条件，而Hin＜0则对应潜在压实局部化失稳。

2 多孔岩体压实局部化理论预测

2.1 多孔岩体弹黏塑性模型

将上述理论与一种应变硬化弹黏塑性本构模型相结合，该模型由Nova等［17］提出，包含了硬化和软化的相互竞争机制。屈服函数（当h=F时，代表屈服函数）及塑性势函数（当h=Q时，代表塑性势函数）表示为

通过标定参数M h、μh及αh，可灵活控制式（13）中给出的屈服面和塑性势面的形状。模型中的硬化变量率和可表达为

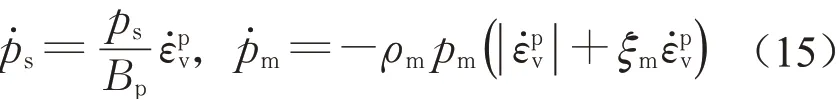
式中：Bp、ρm及ξm为材料参数。ps可用于捕捉由于孔隙变化导致的硬化或软化机制，其中塑性体积应变反映孔隙的变化。多孔岩体压缩变形时，颗粒孔隙会明显减小，这一物理过程可由ps反映，而pm则同时通过体积塑性应变和等效塑性剪应变引入软化机制。

利用式（3），该模型可转变为弹黏塑性模型，黏塑性应变可通过式（16）求得：

式中：pc0为pc的初始值；ω为黏性参数。模型的弹性部分采用线弹性模型。

根据上述模型，Marinelli和Buscarnera［18］基于三轴试验结果及变形分叉理论，标定了多种多孔岩体材料参数，标定的Berea砂岩材料参数如表1所示。基于所建立的本构模型开展有限元数值模拟，在不同围压（p0=75 MPa、150 MPa、200 MPa以及300 MPa）下模拟得到的力学响应与三轴试验结果对比如图2所示，两者较为符合。

表1 Berea砂岩材料参数［18］Tab.1 Material parameters of Berea sandstone[18]

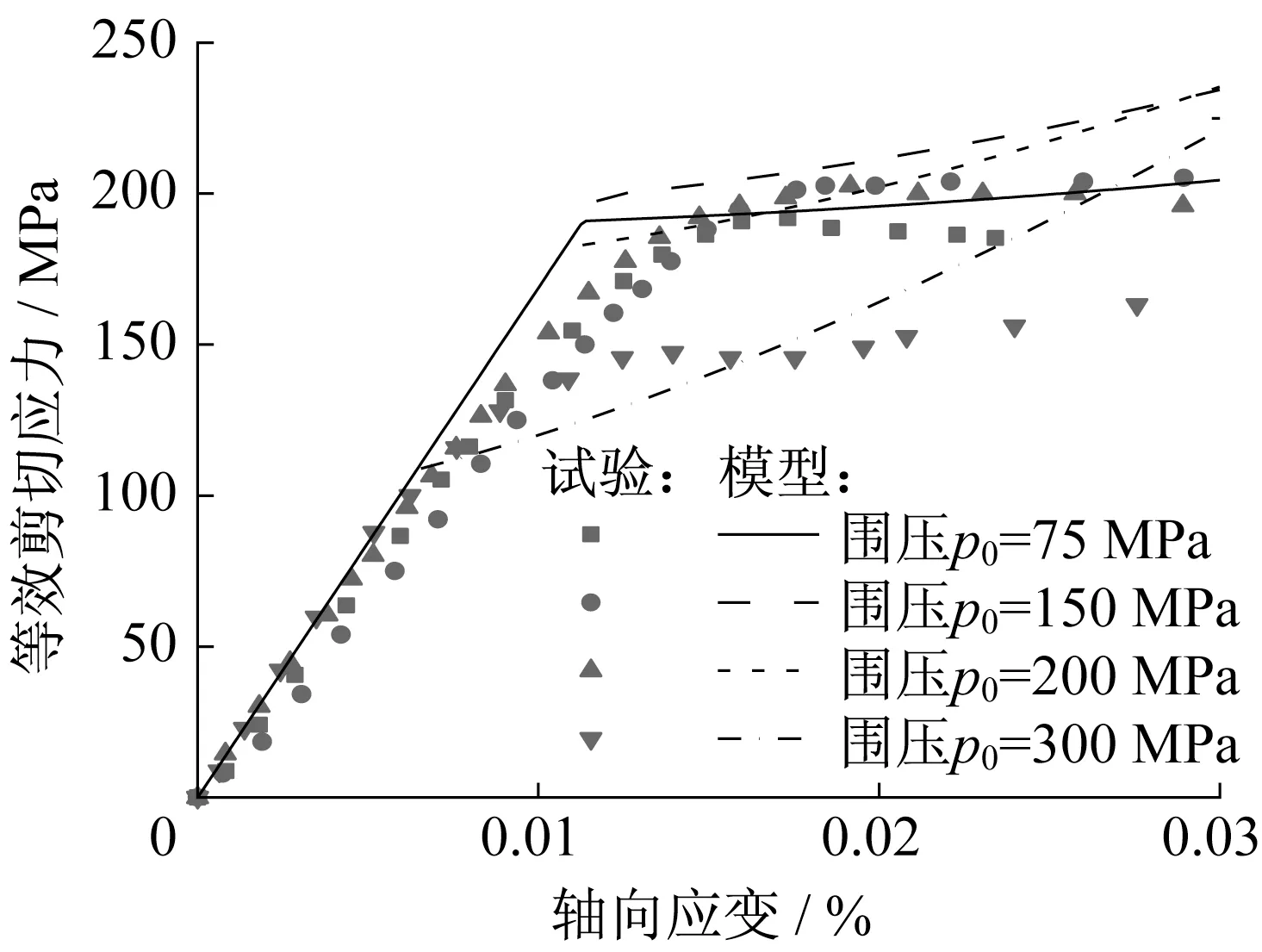
图2 Berea砂岩力学响应Fig.2 Mechanical response of Berea sandstone

2.2 平面应变单元压实局部化分析

进一步地，对平面应变状态下延迟压实局部化进行分析。将平面应变单元视为一个积分点，验证所提出的黏塑性压实局部化失稳指数的适用性。分析包括：①各向同性压缩，使模型具有初始围压；②平面应变剪切模拟，使模型进入非弹性状态；③改变约束条件，使模型进入蠕变变形状态。对于分析步②，当应力状态达到初始屈服面时，对应于某个角度的失稳指数可能变为零乃至负值（即Hin(θ)≤0），此角度即为可能发生的压实局部化带倾角。当存在Hin(θ)≤0时，Hin(θ)最小值对应的角度为最可能出现的局部化带倾角，即A(θmin)=minA(θ)。在各种可能的局部化变形中，A(θ=0)＜0时发生的变形称为压实局部化变形。这种情况下，倾斜角度为0°的局部化带成为一种潜在可能。这种压实局部化变形又分为2种情况，其一为A(θmin)＜A(θ=0)，具有非0°倾斜角的剪切增强压实带；其二为A(θmin)＜A(θ=0)，具有0°倾斜角的纯压实带。在随后的分析步③中，将约束条件更改为与该倾角对应方向施加简单剪切蠕变变形。应注意到，分析步③所施加的控制条件体现了压实变形带内的变形运动特征。

为研究当应力路径达到不同屈服面区域后的模型响应及失稳指数变化规律，选择p1=105 MPa、p2=190 MPa这2种围压开展Berea砂岩模拟，计算结果如图3所示。应力路径与屈服面的交点分别为屈服点Ⅰ和屈服点Ⅱ，由于黏塑性理论允许应力状态超越屈服面，采用围压p1和p2计算所得应力状态与屈服面变化的不匹配造成了变形特性的差异。当应力状态达到屈服面时，应力状态增长速度大于屈服面扩展速度，此阶段为不稳定蠕变变形阶段，可产生由加速变形造成的蠕变压实局部化失稳；而当应力状态增长速度逐渐小于屈服面扩展速度时，不稳定蠕变响应转化为稳定蠕变响应，此时出现的压实局部化为稳定变形。针对屈服点Ⅰ和Ⅱ的所有倾角失稳指数计算结果如图4所示，从图中可看出，基于所提出失稳指数的压实局部化理论预测与基于传统分叉理论的预测结果相匹配。这2种理论所得结果表明：屈服点Ⅰ点的应力状态对应倾角为±21°的剪切增强压实带；屈服点Ⅱ点预测得到倾角为0°的纯压实带。蠕变阶段轴向应变的演化如图5a所示，轴向蠕变应变最开始呈现为加速不稳定发展，随后应变率逐渐降低至趋于零，轴向应变达到稳定值。根据图3结果可知，应力状态和屈服面演化速率不匹配造成了应变加速（或减速）演化，因而应力状态增长速度等于屈服面扩展速度时对应的时间点即为从不稳定蠕变到稳定蠕变的转折点（实心点标出）。图5b表明，围压p1和p2条件下的失稳指数最初为负值，亦即式（8）中弹黏塑性算子的特征值为正，表明轴向应变呈加速变化趋势，即发生不稳定蠕变。随着蠕变变形发展，特征值由负值转化为正值，即逐渐进入减速变形阶段。图5b中失稳指数正负号的转折点与图5a不稳定蠕变转折点一致，说明所提出的黏塑性压实局部化失稳指数能有效识别蠕变的加速失稳和减速稳定阶段。

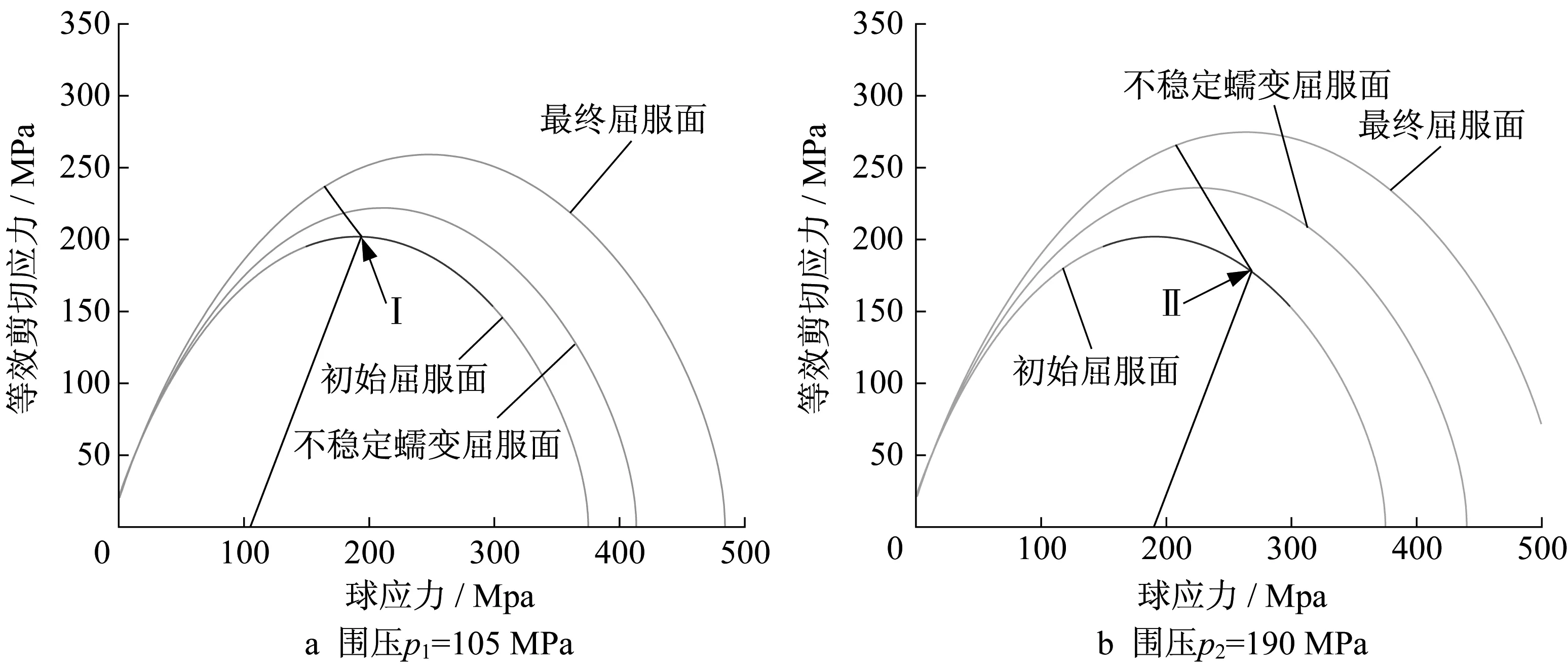
图3 材料点应力路径分析Fig.3 Stress paths of material point analysis

图4 分叉理论与失稳指数计算结果对比Fig.4 Comparison of the bifurcation theory and the instability index

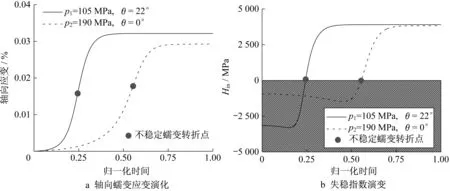
图5 Berea砂岩剪切蠕变分析Fig.5 Analysis of simple shear creep of Berea sandstone

3 多孔岩体压实局部化有限元模拟

进一步开展Berea砂岩局部化形成过程的平面应变有限元数值模拟。分析模型及网格如图6a所示，模型长宽比为2：1，由12 800个C3D8单元组成。底部边界施加全约束，顶部按应变速率10-5s-1施加荷载，以使区域内每个高斯点的应力状态达到屈服面，然后将顶部的牵引力保持恒定，以确保试样可以在固定的外部扰动下随时间蠕变。值得注意的是，这里有限元计算模拟所采用的参数、轴压、控制条件以及加载量与第3节点积分理论分析完全相同。为了触发应变局部化，在模型中间设置了一个薄弱区域（将pc取为原值的95%）。

Berea砂岩有限元数值模拟结果如图6b。由图可见，一旦应力状态进入塑性区（T/Tc=0），在围压p1和p2条件下计算得到的塑性体积应变场呈压实局部化变形模式，且得到的局部化带倾角与材料点预测结果完全一致。图6b还体现了恒定轴向应力作用下体积塑性应变的空间传播模式。在围压p1和p2条件下所得的体积塑性应变首先从薄弱区域出现，然后在模型内部形成多条压实带，这种压实带的形成意味着可能发生局部化失稳。从位于压实局部化带内的高斯积分点获得的局部响应如图7所示，围压p1和p2计算结果中提取的高斯点（图6中灰色星号示出）显示出最初的加速趋势（即不稳定）以及随后的减速趋势（即稳定）。塑性体应变区域内的稳定和不稳定应变响应分别与对应倾角的失稳指数的正负号有关（即倾角为21°和0°分别对应Hin(θ=21o)和Hin(θ=0o)）。分析结果表明，所提出的黏塑性压实局部化失稳指数能很好地用于率相关多孔岩体中压实局部化的分析。

图6 Berea砂岩平面应变压缩试验模拟Fig.6 Numerical simulations of plane strain compression test for Berea sandstone

图7 Berea砂岩有限元高斯积分点分析Fig.7 Finite element Gaussian point analysis of Berea sandstone

4 结语

基于黏塑性假设及压实带内变形运动学特性，建立了描述多孔岩体蠕变条件下应变局部化响应变量随时间演化的常微分方程组，并提出了一个判别多孔岩体蠕变诱发延迟局部化的黏塑性压实局部化失稳指数。进一步地，采用能捕捉不同应变局部化模式的弹黏塑性应变硬化及服从非关联流动法则的本构模型，开展了材料点失稳分析及有限元模拟，结果表明：①通过建立的理论，在加载阶段不同压实应变局部化模式的预测结果与率无关弹塑性变形分叉理论预测结果一致；②蠕变过程模拟中响应变量的加速和减速是由超过弹性域的应力状态与屈服面之间的相对运动引起的，而失稳指数的符号变化（由负到正）对应了响应变量由加速向减速演化的转折点。这些结果表明，文中提出的失稳指数能够合理判别多孔岩体蠕变压实局部化现象。

作者贡献声明：

薛大为：理论推导、程序编写及稿件撰写。

吕玺琳：提出研究思路和方法、稿件审核。

任中俊：结果校核、稿件撰写。

刘泳钢：方案设计、稿件修订。